自组织表征理论下解决原始物理问题的策略

高柏林 侯中柱

摘   要：为了深入解决原始物理问题，教师们以北京师范大学邢红军教授提出的自组织表征理论为基础，介绍了自组织表征理论的含义及实践意义，以及以此为基础解决原始物理问题的五条策略和研究方法，即演绎问题、物理建模、科学推理、知识建构、应用规律，以期给广大物理教师以启示。

关键词：中学物理；自组织表征理论；原始物理问题；策略研究

中图分类号：G633.7    文献标识码：A    文章编号：1009-010X（2023）14-0058-07

原始物理问题（Primitive physics problem），又称为现实问题，是物理学习的根基，是自然界及生活生产中客观存在并且没有被加工的物理现象及规律的真实描述，是最真实、最原始、且高度原生态性的物理问题。物理中的绝大多数问题都是在原始物理问题的基础上通过融入一定的情境然后经过改编、概括、抽象等形成的，是在一定程度上进行抽象化形成的问题。学生在解答这些原始物理问题时无须复杂的科学思维，如概括、建模、推理、赋值等，只需要根据原始物理问题直接解答即可，所以无法感知原始物理问题背后隐藏的深奥物理知识及演绎出的相关物理问题。为了既解决原始物理问题，又让学生在解决原始物理问题的过程中学习到物理知识，实现科学思维、物理方法的综合应用，需要教师发展学生的科学思维，提升学生的核心素养。

为了在解决原始物理问题的过程中实现科学思维、物理方法地综合应用，本文以北京师范大学邢红军教授提出自组织表征理论为基础，介绍了自组织表征理论的含义及实践意义，以及以此为基础解决原始物理问题的五条策略和研究方法，即1.结合生活素材，演绎常见问题，以调动学生的学习积极性；2.结合实际情境，建构物理模型，以培养学生的科学建模能力；3.结合感知的现象，实现科学推理，以助推学生科学思维的发展；4.结合认知冲突，关注知识建构，以提升学生科学分析问题的能力；5.结合生活实际，应用物理规律，以培养学生进行综合实践活动的能力。

一、自组织表征理论的含义及实践意义

自组织表征理论（Self-Organization Repre-sentative Theory），简称SORT，是解决原始物理问题的一种基本方法。其认为问题的解决是一个动态的过程，问题表征贯穿从问题呈现到问题解决始终。这里的问题表征是答题者根据问题呈现的信息，结合自身已有的认知水平、知识经验等，发现问题结构，构建问题空间的过程，也是让研究问题及研究问题的过程、方法呈现出来，使问题解决清晰化的过程。在此基础上北师大邢红军教授提出了解决原始物理问题的自组织表征理论，其认为解决原始物理问题应包括以下七个表征层次，即定向表征、抽象表征、图像表征、赋值表征、物理表征、方法表征、数学表征。本文以北师大邢红军教授提出的解决原始物理问题的自组织表征理论为依据，将自组织表征理论融入到解决原始物理问题的始终，以期为广大物理教师提供参考。

（一）自组织表征理论的含义

自组织表征理论解决的是原始物理问题而不是平时遇到的习题。笔者结合其理论意义，提出了自组织表征理论的表征层次，如表1所示。

从表1可以看出自组织表征理论的七个表征层次是分明的、清晰的，在解决原始物理问题的过程中这些表征不一定是依次出現的，有可能是来回往复出现的。其中最后三个表征“物理表征、方法表征、数学表征”是习题解答的过程，也是为学生提供正确答案的表征过程。由此可以看出，问题解决是一个动态的过程。

（二）自组织表征理论的实践意义

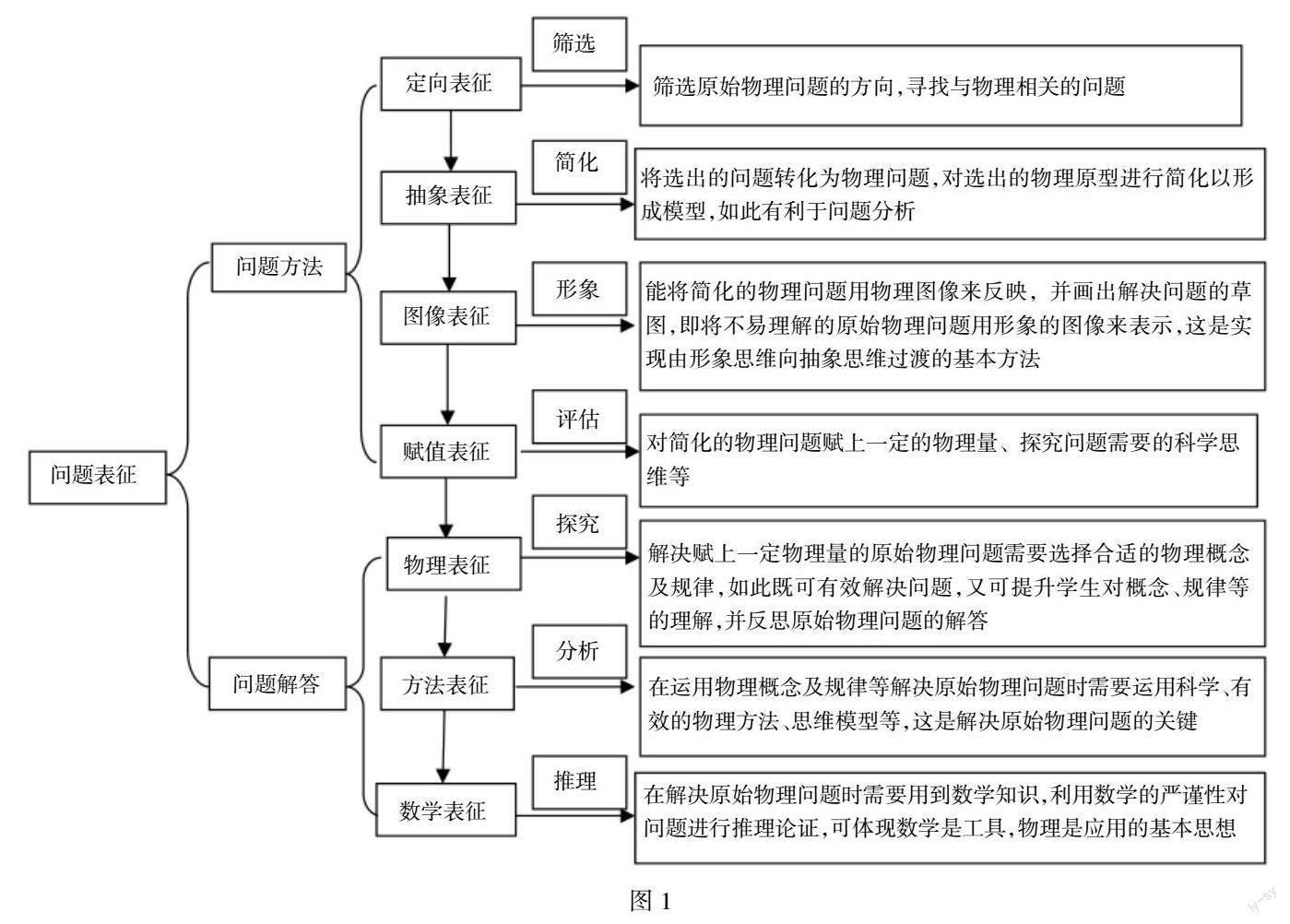
自组织表征理论下的七个表征层次条理清晰、思路明朗，每一个表征层次都对应一种思维形式，因此每一个表征层次在解决原始物理问题的效果上，既作用不相同，又存在紧密关系，这都依赖于问题解决是一个动态的过程。问题表征贯穿问题解决的全过程，因此自组织表征理论的实践意义可以采用如图1所示来表达，如此可解决学生在原始物理问题解答时所产生的疑惑、思维盲点及方法困惑等。

从图1可以看出，自组织表征理论在解决原始物理问题的过程中离不开学生多种思维活动的参与，其中“定向表征、抽象表征、图像表征、赋值表征”是问题表征的方法，“物理表征、方法表征、数学表征”是问题表征的解答。在解决原始物理问题的整个过程中，各表征层次的水平总体上大致相同。如在定向表征上应会筛选出与物理方向有关的问题；在抽象表征上应会根据物理方向上的问题抽象建构适当模型；在图像表征上应会画出抽象建构模型的解题图形；在赋值表征上应会对画出的解题图形设置适当的物理量；在物理表征上应会利用物理规律解答问题；在方法表征上是物理方法及思维模型的应用；在数学表征上应会将数学与物理有机结合在一起以解决原始物理问题。总之，在整个解决问题的过程中，问题表征是一条纽带，贯穿整个解决问题过程的始终。

二、自组织表征理论下解决原始物理问题的策略

“策略”一词在《辞海》中的解释为为了取得某一成果而采取的方法、途径及手段，本文中自组织表征理论下解决原始物理问题的策略，是指在教学过程中运用自组织表征理论解决原始物理问题的思想、方法和手段，是问题表征对其进行思维加工而形成的方法模式，有利于学生形成解决原始物理问题的基本能力。为此，结合自组织表征理论，笔者提出了解决原始物理问题的教学策略。

（一）结合生活素材，演绎常见问题，以调动学生的学习积极性

物理中绝大多数原始物理问题都与生活实际有着千丝万缕的联系。因此，教师在解决原始物理问题的过程中，应结合生活实际素材，在真实的物理情境下，建构与生活素材有关的物理问题，如此可培养学生解决原始物理问题的能力，并调动其学习的积极性。

案例1：曹冲称象可谓是人人皆知的故事，如图2所示，由此设置的物理问题也是较多的，最常见的是与浮力有关的问题，即假如当时的曹冲将船上的石头全部扔进水中，此时的水面会下降，然后利用定向表征将这种现象还原成原始物理问题，就与漂浮在水面上含有小石块的冰块，当冰块全部熔化后水面会下降是一样的。依据抽象表征，利用小石块在水中的漂浮与下沉两种浮沉条件可以建构测量小石块的密度模型，其所需的器材：水盆、小碗、量筒、足够的水（密度为ρ水）、记号笔，如图3所示，测量小石块的密度具体方法如下：1.如图甲，将小石块放在小碗中，然后将小碗放在盛水的水盆内，并用记号笔在小碗外画出水面的位置；2.如图乙，在量筒中倒入适量水，并记下水的体积为v1；3.如图丙，将小碗中的小石块取出放入量筒中，记下此时小石块与水的体积为v2；4.如图丁，将量筒（图丙）中的水慢慢倒入漂浮在水盆中的空小碗中，直至水面达到标记处，记下量筒中剩余水的体积为v3.

这里的关键是运用物体的浮沉条件建构测量小石块密度的基本模型。即将自组织表征理论下的七个表征层次融入测量小石块的密度之中。

这里运用了等效替代法的基本思想，即小石塊漂浮在水面（小碗）上与在小碗内加水至标记处，两者受到的浮力是相等的，然后对此物理问题赋上一定的物理量与数值，并运用物体的浮沉条件及数学知识就可得出小石块的密度。本问题中小石块的重力为，G石块=F浮=ρ水gv排=ρ水g（v2-v3），即m石块=ρ水（v2-v3），小石块的体积为v石块=v2-v1，小石块的密度为ρ石块=■=■·ρ水.

从实际生活素材中提炼原始物理问题，并针对原始物理问题建立一定的物理原型，然后在自组织表征理论的指导下解决原始物理问题。如此有助于实现原始物理问题的深度解答，并调动学生学习的积极性。

（二）结合实际情境，建构物理模型，以培养学生的科学建模能力

从原始物理问题中筛选出与物理知识相关的问题，然后图像建构物理模型是解决原始物理问题的基本途径之一。这里的物理模型是指通过简化、类比、抽象、理想化等方法对物理过程或物理对象进行分析，忽略次要因素，抓住主要因素，从而将客观事物的本质特征凸显出来以构成概念、规律等，进而形成的物理模型。在物理教学中，对于一些复杂且不易被感知的知识点，教师可以通过某些具有启发、引导、再现等特点的途径构建物理模型，由此可帮助学生深入理解这些知识点。如在研究磁场有哪些性质时，教师可引入磁感线来描述磁场的分布情况，这就是模型法；还有为了研究光而引入光线等，这些都是模型法在解决原始物理问题中的应用。

案例2：蹦极（又名机索跳）是一项非常刺激又冒险的户外活动，运动员往往是站在40m高的塔顶上参加该项活动，这是一个典型的原始物理问题，涉及物理、化学、数学等多学科知识，因此可以通过自组织表征理论来研究其中的原始物理问题。具体过程是：首先将蹦极的整个过程简化为图甲，即运动员从塔顶O点开始下落，下落到A点时弹性绳自然伸直，到B点运动员所受的弹力恰好等于重力，C点是运动员第一次下落到的最低点，运动员在整个蹦极过程中所受弹性绳的弹力F大小随时间t的变化情况如图乙所示（为了在初中物理范围内研究蹦极过程，教师通过理想化模型将整个蹦极过程视为一直在竖直方向上的运动）。分析图乙与图丙，经总结概括可将整个蹦极过程中弹性绳弹力F大小随时间t的变化情况视为弹簧模型，具体分析过程如表2所示：

从对弹簧模型的分析可知，整个过程中是重力势能、弹性势能、动能之间的相互转化，最终重力势能将全部转化为弹性绳的弹性势能，这时运动员静止于B点处。过程细节分析：运动员在B点时G=F，结合图像乙可知，运动员经过整个运动过程并最终静止在B点（弹力F大小保持不变）时的弹力F=0.6F0，即G=0.6F0；t0时刻运动员的弹性势能最大，动能为0.

在实际情境中，有些物理问题、现象、过程复杂且抽象，这时可以通过建构与此相关的物理模型，来简化并解决该问题。如整个蹦极过程比较复杂，对此，教师可以通过建构弹簧模型来帮助学生分析该过程，如此就可以使原始物理问题变得形象、直观，然后在此基础之上激发学生的科学思维，就可达到解决原始物理问题，甚至解决一类问题的目的。

（三）结合感知的现象，实现科学推理，以助推学生科学思维能力的发展

人们所感知的生活现象是原始物理问题素材的来源与途径之一。在物理教学中，教师不仅要关注科学探究过程以得出物理规律，还要注重探究过程中学生推理能力的培养，如此既可以提高学生对科学探究的兴趣，促使科学探究、科学态度以及科学精神等在解决原始物理问题的过程中得到有效落实，又可以助推学生科学思维能力的发展。

教师可根据生活中能直接感知的物理现象，通过科学推理得出无法直接感知的物理事实，这种科学推理是物理教学中常见的一种科学思维。如图5所列举的几个常见的物理事例，都是结合物理研究方法，应科学推理从最常见的感知现象中提炼出的物理概念、规律等，这种原始物理问题的解决是以自组织表征理论为基础，以科学思维发展为根本目的的解决原始物理问题的教学模式之一。

案例3：如在讲授“阻力对运动物体的影响”时，从图6中小明和小华对物理现象描述的基本对话中可筛选出与物理相关的知识。学生之前产生的错误认知，即物体的运动需要力来维持，可以通过实验来驳斥和解决。即教师在课堂上出示事先准备好的器材：斜面、小车、长毛巾等，如图7所示，将长毛巾平铺在水平面的木板上，然后让小车从斜面顶端静止滑下，由此可观察到小车在水平长毛巾上滑行一定距离后静止，然后将长毛巾去掉，重复实验，可观察到小车在水平木板上的滑行距离变长，这时如果进一步减小小车在水平木板上的阻力就会发现小车的滑行距离将变得更长，然后进一步推理可知，如果水平面绝对光滑（即理想情况下），小车在水平面上则不受阻力，这时小车在水平面上将永远运动下去（做匀速直线运动），以上通过科学推理反驳了物体的运动需要力来维持这个错误观点。

（四）结合认知冲突，关注知识建构，以提升学生科学分析问题的能力

自组织表征理论下，结合认知冲突是解决原始物理问题的一种有效方法。在此过程中教师可以充分利用知识建构来提升学生科学分析问题的能力。如在杠杆学习中撬图钉是一个原始物理问题，利用这个模型可以巧妙引入杠杆五要素，其中力臂的概念是杠杆五要素中最抽象、最不易理解的概念。

案例4：综合各大版本的教材笔者发现，力臂概念的引入往往是通过教师的直接讲解，或通过数学上作垂直图等来实现。如图8所示，这是对原始物理问题的数学化，但其无法使学生深入理解力臂的概念。为此，教师可以利用力的三要素与二力平衡等知识来引入力臂的概念，即以二力平衡的条件与杠杆平衡时产生的认知冲突为起点，激起学生在建构力臂概念时的认知冲突，如此可使学生进一步认识力臂及杠杆五要素。

实验原理：学生自主参与活动，利用力的三要素、二力平衡的知识与杠杆平衡的知识产生认知冲突。

实验准备：几只铅笔、教科书多本。

实验过程：学生在教师的指引下利用实验准备时的学习工具，按照如图9所示的方式进行探究实验。即将两只铅笔十字交叉叠放在一起，然后用自己的一只手指轻轻按压一只铅笔的一端，如此就可将多本教科书轻轻抬起，并保持静止状态，然后将手指按压的一根铅笔当杠杆，其中交叉点为支点O.

力臂概念的建构：谈力需要涉及力的三要素，即力的大小、方向、作用点。对杠杆的受力分析也需要分析力的三要素以及二力平衡的条件，二力平衡的条件即作用在同一物体上的二个力，力的大小相等、方向相反、作用于同一条直线上。此时的杠杆（铅笔）处于静止状态，即保持平衡，手指对铅笔的力的方向向下，教科书对铅笔的力的方向也向下，且两个力既不在同一个方向上又不在同一条直线上，那么，铅笔为什么能够保持平衡呢？

“铅笔为什么能够保持平衡”激起了学生原有认知结构与新概念产生的认知结构之间的矛盾，即产生了认知冲突——难道之前学习的力的三要素、二力平衡等知识存在错误的地方？这是不可能的。如此就可以水到渠成地引入力臂L的概念，原来在杠杆平衡的条件中，还存在另外一个与杠杆有关的因素，即力臂，其也能决定杠杆平衡。然后教师再通过刚才铅笔抬起教科书的探究实验，向学生介绍杠杆中动力F1、阻力F2、动力臂l1、阻力臂l2、支点O，由此引出杠杆五要素可以说是完美无瑕的。

学生往往对通过认知冲突解决的原始物理问题印象很深。这是因为其不仅解决了当下的原始物理问题，还联系了与此相关的其他问题，可谓是一举多得，同时还可提升学生科学分析问题的能力。

（五）结合生活实际，应用物理规律，以培养学生进行综合实践活动的能力

原始物理问题中有部分是生活实际问题，即将物理规律融入生活实际，体现了物理规律在生活中的基本应用。学习物理的根本目的就是应用物理规律解决实际问题，特别是最基本的原始物理问题，其既可以培养学生的物理学习兴趣，又可以培养学生解决实际问题的能力。

案例5：杆秤是生活中常见的测量质量的基本工具之一，实际上杆秤不仅可以测量质量，还可以测量液体的密度，为此，某中学八年级（8）班同学在综合实践活动中自制了能够测量液体密度的杆秤密度计，这样可以从杆秤上的刻度直接读出液体密度的大小，设计如图10所示。

器材：轻质杠杆（自身重力忽略不计）、100mL空桶、秤砣mA、刻度尺、细线。

设计过程如下：

1.先确定密度为零的刻度位置，方法是在O点将杆秤悬挂起来，在B点悬挂空桶，改变秤砣mA的位置到C点时杠杆水平平衡，这时用刻度尺测量BO的距离为l，CO的距离为l0，则C点即为液体密度为0时的位置。（根据杠杆平衡条件得出mBg·l=mAg·l0）

2.這时可以在B点的空桶内（容积V）注满液体（或一定标记处），然后改变秤砣mA的位置到C1点时杠杆水平平衡，这时用刻度尺测量C1O的距离为l1，此时可以从杆秤上的C1点直接读出液体密度的大小，具体刻画密度值大小的方法如下：

在解决原始物理问题的过程中往往需要将物理规律与生活实际相结合，因此要注重物理规律在解决生活实际中原始物理问题过程中的应用。如此既可以让学生感知到原始物理问题与物理规律之间的紧密联系，又可以培养学生进行综合实践活动的能力。

自组织表征理论下解决原始物理问题的关键是将原始物理问题物理化，物理问题问题化。如此可使学生明白解决原始物理问题不仅仅是解决问题本身，更重要的是以原始物理问题为起点，解决问题背后隐藏的更深层次的物理知识，然后再将物理知识应用到物理学习当中去，这就是从问题中来，再回到问题中去，即自组织表征理论下解决原始物理问题的本质所在，如此可提升学生的核心素养。