基于概率滑行时间的航空器离场推出柔性控制
张颖,黎晓英,尹嘉男,,周笑桐
1.南京航空航天大学 通用航空与飞行学院,南京 210016
2.国家空管飞行流量管理技术重点实验室,南京 210016
3.南京航空航天大学 民航学院,南京 210016
机场场面离场活动一般由撤轮挡、推出、滑行、等待、起飞等过程构成,该过程具有高度的复杂性、动态性和易扰动性,极易引发密集性场面冲突和持续性拥堵延误,是航班“门到门”全生命周期运行中的关键阶段。场面离场阶段极易产生多类型的航班延误,具体涵盖停机位等待、推出等待、滑行道等待、机坪等待和跑道头等待[1]。在此背景之下,如何科学预测和控制航班离场活动,尽可能地将高成本的滑行等待和跑道头等待转变为低成本的机位等待,成为当前航空运输业界和学界亟待解决的关键难题。
然而,场面滑行过程极易受机场设施状况、资源配置方案、航班过站保障、外围流控限制等内外部因素影响,滑行时间具有较强的随机性和不确定性,对其进行准确预测的难度较大,而不准确的预测更使离场推出控制决策缺乏科学依据,进而导致场面离场运行性能较为低下。若航班推出过晚,可能因无法在计划时间起飞而导致航班延误;若航班推出过早,又可能因场面资源使用冲突而导致不必要的排队等待、燃油消耗及航空排放。因此,亟需研究考虑滑行时间不确定性基础上的航空器离场推出的柔性控制关键技术。
目前,国内外相关学者针对滑行时间预测与离场推出时间控制问题已开展了大量研究。在滑行时间预测研究方面,主要采用仿真建模和分析建模两类方法。其中,仿真建模通过对机场物理结构进行拓扑建模,模拟所有进离场航空器的场面活动过程,在对航空器场面运行冲突进行探测和解脱的基础上计算滑行时间[2]。分析建模主要采用线性回归等统计学方法和成熟典型的机器学习算法[3]。例如,Idris等[4]对队列长度、跑道配置、天气条件等影响滑行时间的主要因素进行了分析,以起飞队列长度这一指标为关键影响因素,建立了航班离场排队模型对滑行时间进行预测;Ravizza等[5]将滑行距离分为推出段、转弯段和直线段,研究了航空器经过各类路段的滑行速度和转弯角,结合机场布局和历史滑行信息建立了基于多元线性回归的离场滑行时间预测模型;Yin等[6]充分考虑进离场航空器耦合交互行为,建立了场面进离场时空分布宏观网络,通过将滑行数据进行对数转换,使用6种曲线回归模型对滑行时间进行了预测。近几年,亦有学者利用强化学习、支持向量机、K近邻、随机森林和神经网络等机器学习算法,对历史滑行数据进行挖掘分析,进而预测场面滑行时间[7-8]。例如,Lee等[9]建立了基于随机森林的场面滑行时间预测方法,并与场面运行仿真得到的预测结果准确率进行了对比分析;李楠等[10]分别采用传统统计学多元线性回归模型和Lasso回归模型预测航空器离场滑行时间,并对预测准确度进行了对比分析,验证了所用机器学习方法的优越性。
在离场推出时间控制研究方面,Feron等[11]最早采用N-control推出策略,根据场面离场航空器数量与设定阈值之间的关系来决定航空器是否在特定时段完成推出;Simaiakis等[12]提出了“推出率控制”的概念,给出建议的离场航班推出率,从而有效避免机场场面进入拥挤状态并减少航班滑行所需的时间,该方法相比N-control推出策略对管制运行的干预更少;Desai等[13]提出了一种推出率随滑行道排队长度变化的推出控制方法;Mori[14]通过引入固定缓冲时间,综合利用跑道计算起飞时间、确定性的滑行时间与固定缓冲时间等信息,计算具有鲁棒性的离场推出时间;Badrinath等[15]采用拓扑理论与图论方法,对场面“节点-链接-路网”等结构要素进行精确建模,建立了场面四维轨迹优化模型和基于排队论的离场计量模型,对推出时间、滑行路径、各滑行段运行速度、以及跑道头等待时间等进行整体优化。
可以看出,当前研究工作虽取得一系列显著成果,但仍然存在以下不足:其一,当前对场面滑行时间的预测结果主要聚焦个体滑行时间“点值”估计和群体滑行时间“分布”估计[14],无法给出概率化的个体滑行时间“范围”估计,不能较好地体现单架航空器滑行过程的高度动态和随机扰动特性;其二,当前对离场推出控制的研究成果主要聚焦“交通量”视角下的“推出率”控制和“延误转换”视角下的“推出时间”控制,且推出时间的控制过程不考虑滑行不确定性引发的扰动问题,不能较好地实现滑行时间与起飞延误之间的最佳权衡;其三,当前对“推出时间”的控制决策过于刚性,没有充分考虑不确定滑行时间下的柔性化推出控制问题,无法给出更为合理、实际操作性更强的离场推出时间范围,极易导致推出至起飞过程产生更多的场面冲突和延误。
鉴于此,本文针对上述传统离场滑出时间采用确定性点估计预测而无法反映预测滑行时间本身的不确定性特征,以及离场推出控制采用刚性约束导致管制灵活性低等问题,以离场滑行时间的“概率化”预测和离场推出过程的“柔性化”控制为特色,研究基于概率滑行时间的航空器离场推出柔性控制问题,旨在通过科学估计离场航空器滑行时间的概率分布范围,实现离场推出“时刻”和“时隙”的多视角柔性控制,从而可用于支撑当前机坪管制移交背景下的推出时间决策,为机场实际运行控制的灵活和高效等性能提升提供新的研究思路,切实增强机场实际运行中离场推出时间控制策略的有效性及鲁棒性。
1 机场数据分析与实验样本
本节针对中国旅客吞吐量在千万级以上的昆明长水国际机场,对其场面物理结构数据和交通运行数据进行了分类采集与定量描述,并对航班排队、资源调度、公司属性等影响航空器场面滑行时间的各类因素进行了分析和提取。
1.1 数据描述
目前,昆明长水国际机场的日航班起降架次在1 000左右,拥有2条跑道,东侧跑道方向为22/04,西侧跑道方向为21/03,以22、21跑道方向为主起降方向,主要采用“相关进近、独立离场”跑道运行模式。
表1所示为研究时段内的离场航班数据结构,主要包括航班号、机型、起飞跑道、停机位、航线、实际推出时间和实际起飞时间等。

表1 离场航班数据结构Table 1 Data structure for departure flights
1.2 滑行时间影响因素分析
根据中国民用航空局机场协同决策(Airport-Collaborative Decision Making, A-CDM)规范[16],航空器离场滑行时间指航空器起飞离地时刻与撤轮挡时刻之差。航空器滑行过程受诸多因素影响,基于对昆明长水机场运行环境的分析与运行数据的挖掘,本文重点选取停机位、航空公司、推出时段、场面流量和排队指数5个因素,分析其对场面滑行时间的影响。
1)停机位
在机场实际运行过程中,管制员会根据停机位、起飞跑道等资源调度方案,从航空器滑行路径候选集中选择相应的滑行路径对航空器场面运行进行引导和控制。如图1(a)所示,航空器从不同的停机坪区域的停机位推出时,由于特定停机位推出限制、场面滑行距离以及滑行过程中的进离场航空器交互均存在一定差异,其滑行时间亦存在明显差异。

图1 滑行时间影响因素Fig.1 Influencing factors of taxiing time
2)航空公司
在特定的航空运输机场,不同航空公司具有基地与非基地的差异化属性,且航空器滑行速度、资源使用的优先权、冲突调配的优先权、航班延误的波及性等均存在差异,上述因素势必影响航空器滑行过程。如图1(b)所示,不同航空公司的航空器平均离场滑行时间存在显著差异。
3)推出时段
机场一天内各时段具有不同的场面交通繁忙度,尤其是早晚高峰时段具有高度密集的飞行流量,而不同繁忙时段内航空器之间的耦合交互程度不同,进而导致滑行冲突频次和滑行时间大小均存在时段差异。为此,本文引入推出时段作为滑行时间的关键影响因素,通过统计各小时推出航空器的数量以及该时段内航空器平均滑行时间作为衡量场面交通状况的重要指标。由图1(c)可以看出,航空器推出时段对航空器平均离场滑行时间具有一定程度的影响,且不同推出时段进离场航班架次、采用的跑道运行模式均会影响离场航班推出时间。整体而言,离场推出航班数量越大的时段,离场平均滑行时间也越大,部分时段也存在一些不一致的变化趋势:03:00—05:00时段,机场实施单跑道运行模式,该时段推出的航班架次少并且不能就近起飞,从而导致整体滑行时间反而偏大;08:00—09:00时段离场推出数量并不大,但是由于进场航班的显著增加,导致跑道头排队等待时间增大,进而使得离场航班总滑行时间增大且出现高峰值。
4)场面流量
在场面滑行的航空器流量统计方面,本文采用Yin等[17-18]提出的基于宏观网络拓扑图的场面交通流量计算方法,共统计包括场面离场瞬时流量、场面进场瞬时流量、场面离场累计流量、场面进场累计流量、离场时隙需求指数、进场时隙需求指数等3类6个场面流量指标。场面瞬时流量统计了在参考离场航班d0实际推出时,场面正在滑行离场和进场的航空器数量。时隙资源需求指数统计了在参考离场航班d0的离场推出时隙δ(单位为min)内推出和降落的航空器数量。场面累计流量统计了场面上进离港航空器的滑行周期与参考离场航班d0整个滑行周期重叠的数量。通过计算上述各指标与滑行时间的Pearson相关系数发现,离场时隙需求指数、场面离场累计流和离场瞬时流量对离场滑行时间的影响较大,Pearson相关系数分别为0.427、0.249和0.215。离场滑行时间随离场时隙需求指数和场面离场累计流量的变化趋势如图1(d)~图1(e)所示。
5)排队指数
由于昆明长水机场主要采用“相关进近、独立离场”跑道运行模式,2条跑道均可同时用于起降,进离场航空器对跑道资源的占用使得场面排队现象较为常见,航空器实际滑行时间亦会受到场面队列长度的影响。本文采用的航空器排队长度指数主要包括离场排队指数(Departure Aircraft Queue Length Indices,D_AQLI)和进场排队指数(Arrival Aircraft Queue Length Indices, A_AQLI),分别表示航空器在整个滑行过程中跑道上起飞和降落的航空器数量。通过计算A_AQLI和D_AQLI与滑行时间的Pearson相关系数发现,A_AQLI对滑行时间影响更大,Pearson相关系数为0.58,D_AQLI与滑行时间的相关系数为0.281。图1(f)箱线图显示了离场航空器的实际滑行时间随进港航空器排队指数的变化情况,随着进港航空器排队指数的增加,离场滑行时间的中位数显著增加,主要原因在于进港航空器的排队需求指数越大,航空器发生跑道头等待的几率便越高,进而导致航空器的实际滑行时间亦随之越大。
1.3 实验样本选取
以昆明长水机场2019-09-01—2019-12-31的离场航班实际运行数据为样本数据集,使用随机采样法划分训练集和测试集,通过对不同划分比例的预测效果进行比较,选定80%的数据作为训练集,样本数为45 120 条,其余20%为测试集,样本数量为11 280 条。
对原始数据的预处理操作主要包括筛选并删除异常值、使用中位数填充空缺值,以及文本和类别属性的处理等,并将数值型变量采用Pearson 相关系数对其与滑行时间进行相关性强弱分析,类别型变量则采用卡方检验并结合Phi系数来量化每个分类变量与航班滑出时间的相关性强弱。经特征剔除,得到推出时间相关变量(推出月份/推出时段)、场面航班相关变量(航班号/机型/停机位)、交通流相关变量(场面离场瞬时流量/场面离场累计流量/离场时隙需求指数/离场排队指数/进场排队指数)三大类共10个特征变量。表2所示为模型的最终输入数据。

表2 模型输入数据Table 2 Model input data
2 离场航空器概率滑行时间预测
本节采用随机森林回归与核密度估计方法相结合,建立了面向单架离场航空器的场面滑行时间概率化预测模型,提出了基于网格搜索法的预测模型超参数调节策略,并设计了概率预测评价指标对离场滑行时间预测性能进行评价。
2.1 概率滑行时间预测模型
随机森林回归(Random Forest Regression,RFR)是一类基于决策树的集成学习算法,通过构建多棵决策树作为基学习器对同一目标进行学习,对所有决策树的输出值求平均,从而获得样本的点估计预测值。部分研究者基于随机森林回归研究了概率预测方法,主要包括2种思路:一是在决策树生长期间或之前引入随机变量[19-21];二是在不改变随机森林回归算法本来工作方式的前提下,获得所有决策树的确定性预测结果集合,进而获得概率预测结果。本文采用第2种思路,采用核密度估计(Kernel Density Estimation, KDE)方法对决策树的预测结果集合进行处理,获得滑行时间的概率密度函数。概率滑行时间预测的基本步骤如图2所示。
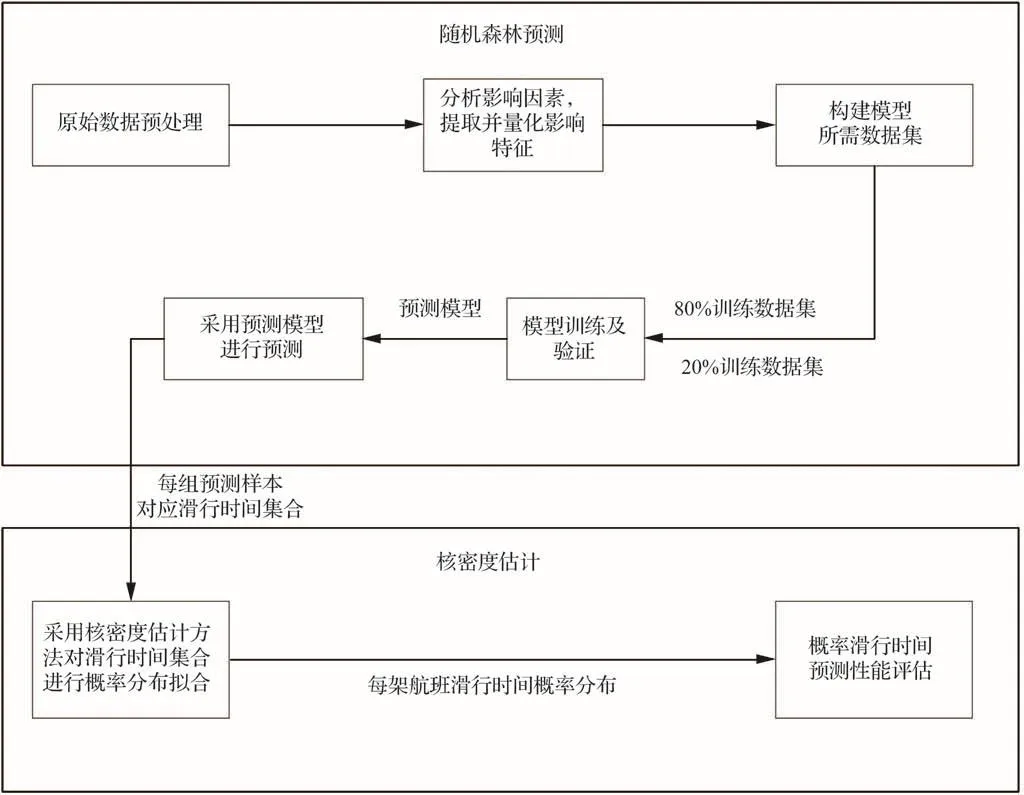
图2 概率滑行时间预测基本步骤Fig.2 Steps for prediction of probabilistic distribution of taxiing time
2.2 概率预测性能评价指标
对于滑行时间点估计预测性能的评价指标普遍采用的是均方根误差 ( Root Mean Square Error, RMSE )和平均绝对误差 (Mean Absolute Error, MAE )。考虑到本文对滑行时间的概率预测特点, 无法应用RSME和MAE等指标,因此定义以下6个指标,对所建概率滑行时间预测模型的性能进行多视角评价分析。
1)连续分级概率评分指标CRPSmean与CRPSstd
连续分级概率评分(Continuous Ranked Probability Score, CRPS)用于评估概率滑行时间与确定性观测样本间的差异,是MAE在概率预测中的推广,CRPS定义为
令p(yi)为滑行时间的概率分布函数,yˉi代表第i架航班的实际滑行时间值,式(1)中F(yi)是p(yi)的累积分布函数,1z≥yˉi是Heaviside阶跃函数。基于单个航班的CRPS指标值,可计算所有航班样本的CRPS均值(CRPSmean)以及CRPS标准差(CRPSstd)。
2)估计分布均值与观测值偏差指标RMSEM与MAEM
由于RSME和MAE不适合评估滑行时间的概率分布,本文提出变量RMSEM和MAEM,用于表征概率预测的平均值与实际滑行时间之间的误差。RMSEM和MAEM的定义分别见式(2)和式(3):
式中:Nf为测试集的航班样本总数;μM(xi)为从每个决策树获得的滑行时间点估计的平均值;yˉi为实际滑行时间。
3)概率分布标准差指标σˉ
各个航班滑行时间的概率分布标准差σ(xi)以及所有航班的滑行时间概率分布标准差σˉ分别见式(4)和式(5):
式中:表示样本i的第j棵决策树的估计值;μM(xi)为随机森林每个决策树点估计值的均值;h为核密度估计的带宽;ne表示决策树的数量;为所有航班滑行时间概率分布标准差σ(xi)的平均值。
引入二进制变量f1σ(xi),若为1则表示实际滑行时间与样本的平均值μM(xi)之间偏差的绝对值小于标准偏差σ(xi);否则,为0。为所有样本Nf中f1σ(xi)的平均值,用于衡量预测滑行时间概率分布接近真实滑行时间值的百分率。和f1σ(xi) 表示为
上述所定义的6个指标中,CRPSmean、CRPSstd、RMSEM、MAEM和σˉ的单位为min,与所预测滑行时间变量单位相同,而¯f1σ为无量纲的百分比数据。
2.3 模型超参数调节策略
为提高概率滑行时间模型的预测效果,采用网格搜索法对模型的关键参数进行优化,基于最低平均CRPS选择相应的超参数。构建了150个最大深度为12层的决策树,对于每个分支划分,叶子节点中最少有7个训练样本,考虑34的特征,表3所示为选定的超参数及其搜索范围。

表3 超参数搜索范围Table 3 Hyper parameter search scope
2.4 概率滑行时间预测结果
基于随机森林算法为每架待预测航班输出各个基学习器的预测结果集合,输出数据如表4所示。采用核密度估计方法,对每组测试样本获得的滑行时间集合进行概率分布拟合。为了使估计的分布更为平滑,核类型选用常见的高斯核,带宽设置为1.5倍。图3所示为滑行时间概率预测结果,其中柱状图表示随机森林学习器的直方图,曲线表示核密度估计从该直方图获得的概率分布。

图3 概率滑行时间预测结果Fig.3 Prediction of probabilistic distribution of taxiing time

表4 模型输出数据Table 4 Model output datamin
为验证概率滑行时间预测模型的性能,使用5 倍交叉验证构建训练集和测试集,计算6 个概率预测性能指标,计算结果如表5所示,采用概率分布逼近度来衡量预测滑行时间均值接近真实滑行时间值的百分率,滑行时间概率分布逼近度为71%,所获得的概率滑行时间作为本文后续提出的离场推出柔性控制方法所需的输入数据。

表5 滑行时间概率预测性能指标Table 5 Performance metrics for taxiing time probabilistic prediction
3 基于缓冲区的离场推出时刻柔性控制
本节基于第2节得到的概率滑行时间,引入固定缓冲区概念,研究离场推出时刻的柔性控制方法,旨在为每架航班设置最优的缓冲区,以确保基于缓冲区计算的离场推出时刻满足准时到达跑道的概率需求。“推出时刻”控制的“柔性”内涵主要体现在机场运行决策人员可对缓冲区长度进行灵活设置,实现滑行时间与准时到达跑道头概率之间的最优权衡。
3.1 缓冲区基本定义
停机位推出时间一般根据跑道计算到达时间减去预计滑行时间得到。根据航班计划到达跑道时间trunway和预测滑行时间ttaxi,不考虑不确定性条件下的理想推出时间应为trunway-ttaxi;考虑滑行时间的不确定性,可以为航班设置一个统一的滑行时间缓冲时间tbuffer,从而得到具有鲁棒性的推出时间tPush=trunway-ttaxi-tbuffer。需说明的是,本文中的航班计划到达跑道时间trunway为跑道进离场管理系统优化后的离场航班起飞时间。
Mori[14]根据跑道虚拟时隙队列中排在前面的航空器架次来确定缓冲区长度,当排在前面的航班架次超出一个预设的值,则缓冲区长度设置为固定值,否则缓冲区设置为无穷大,即航班都安排尽早推出。
为了得到更为合理的离场推出控制时间,需对tbuffer进行科学设置。若缓冲区设置较小,航班推出较晚,按计划到达跑道的概率变小,但航班的总滑行时间相比按照计划推出时间推出情况下的总滑行时间减少量会增大,即航班滑行时间会较小;若缓冲区设置较大,可最大程度地吸收滑行过程中的不确定性,航班按计划到达跑道头的概率增大,但由于推出控制时间过于保守,导致航班的总滑行时间减少量会减小,即航班滑行时间会较大。
3.2 缓冲区优化设置及推出时刻计算方法
本文遵循欧洲空中航行安全组织、中国民用航空局等国内外航空管理机构普遍采用的主流的A-CDM建设规范及运行标准,将跑道进离场调度后的起飞时间(在本文中为已知信息)、预测滑行时间的点估计值及概率分布作为输入信息,来计算离场推出时刻[16,22-23]。
针对当前研究中为所有离场航班设置统一的滑行缓冲区时间的不足,本文将每架航班的差异化概率滑行时间用于缓冲区的柔性设定,所设定的缓冲区进而可用于控制推出时间的计算,计算过程如图4所示。

图4 基于缓冲区的离场推出时刻控制方法Fig.4 Buffer-based pushback time control method
计算流程为:首先,使用随机森林算法预测该天所有航班滑行时间的点估计ttaxi,设置不同的缓冲时间tbuffer,根据tpush=trunway-ttaxi-tbuffer计算出相应的控制推出时间tPush;然后,基于第2节的算法预测概率滑行时间,并根据滑行时间的概率分布计算每架航班在不同的缓冲时间下准时到达跑道的概率pontime,令Φf()表示概率滑行时间的累积分布函数,pontime的计算公式为pontime=p(tpush+≤trunway)=Φf(trunway-tpush)=Φf(ttaxi+tbuffer)。可以看出,随着tbuffer的增加,pontime也增大,在滑行时间超出ttaxi后累积概率的递增率越大,则准时到达跑道的概率增加也越快,若累积概率的递增率很小,则准时到达跑道概率值的增加也较缓慢。通过对航班准时到达跑道的概率随缓冲区大小变化的趋势进行数值分析,可对所需的缓冲区大小进行科学设置和权衡优化,进而基于该优化的缓冲区计算tpush,以确保航班准时到达跑道的概率满足场面运行决策需求。
3.3 缓冲区优化设置计算实例
采用3.1节中的计算方法,使用2019-09-01—2019-10-14的航班作为训练集,将2019-10-15的航班(共415架次)作为测试集。图5给出了典型日随机选取的8架航班准时到达跑道概率随所设置的缓冲区时间的变化趋势。可以看出,不同的航班因所预测的滑行时间的概率分布不同,在相同的缓冲区时间下准时到达跑道的概率不同。图5(a)中,当分别设置1、1.5、2 min的缓冲时间,准时到达跑道头的概率分别为88%、96.9%、98%,继续增加缓冲时间,准时到达跑道头的概率不再明显增加;图5(c)、图5(e)和图5(g)为同类情况,对该类航班可优先选择设置较小的缓冲时间。图5(b)中,在设置1、2、3、4 min的缓冲时间时,准时到达跑道头的概率分别为64.4%、74.9%、84.1%、92.5%,持续设置更大的缓冲时间,准时到达跑道头的概率会进一步增加;图5(d)、图5(f)和图5(h)为同类情况,对该类航班可通过设置较大的缓冲时间来获得较高的航班起飞准时率。综合图5(a)~图5(h)可知,在机场实际运行过程中,可通过历史数据挖掘明确每架航班的实际情况,以此设置更为合理的滑行缓冲时间,从而实现较大的滑行时间减少量与较高的准时到达跑道概率之间的最佳权衡。
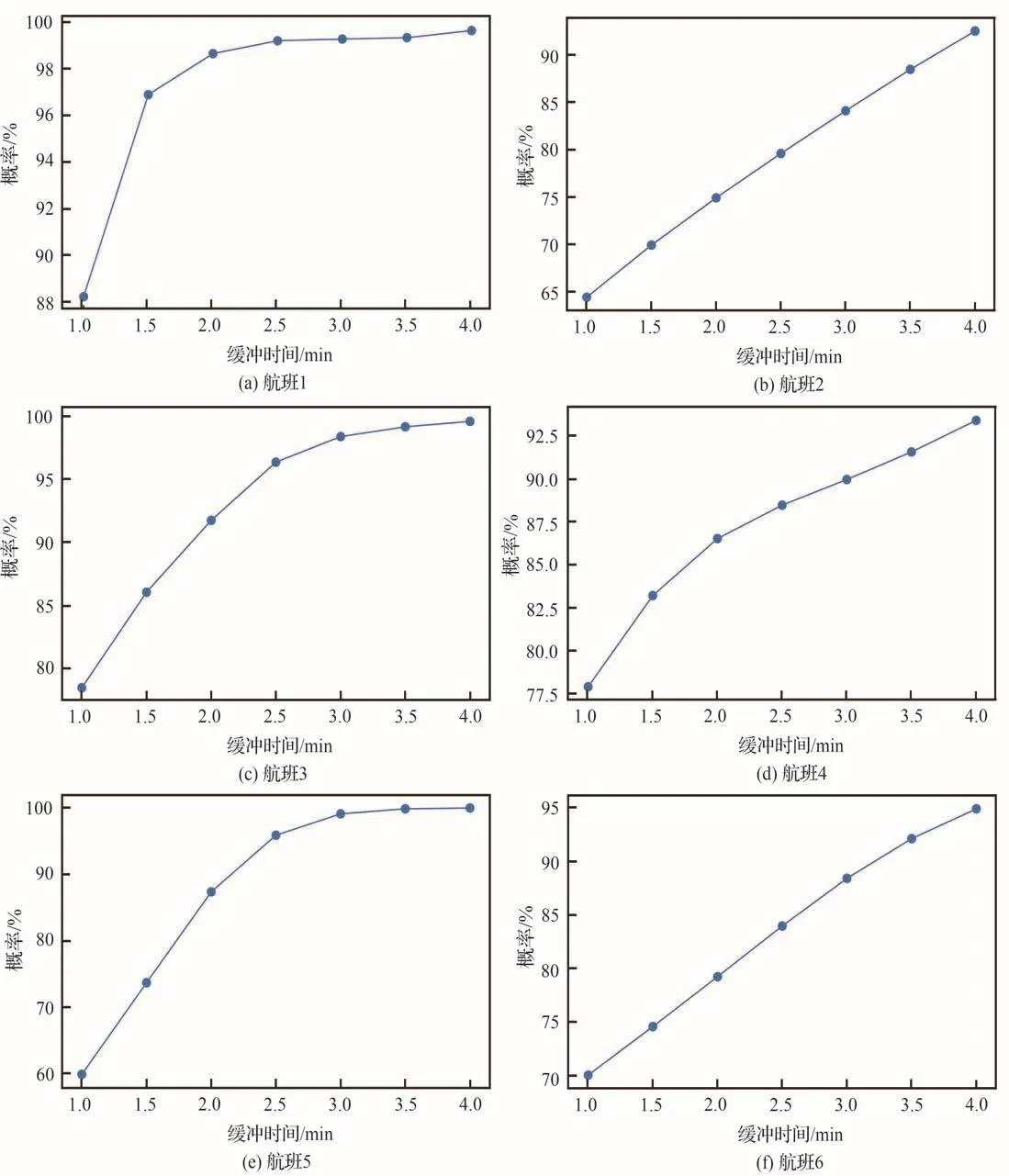
图5 滑行缓冲时间与准时到达跑道概率的权衡Fig.5 Trade-off between taxi-buffer time and probability of arriving at runway on time
4 基于机会约束的离场推出时隙柔性控制
第3节聚焦离场推出“时刻”控制,且准时到达跑道时间的限制条件为单边约束,虽可确保实际到达跑道时间小于等于计划到达跑道时间,但却可能导致较长时间的跑道头等待。为了进一步考虑到达跑道时间的双边约束限制,本节聚焦离场推出“时隙”控制,应用随机规划中的机会约束理论,研究离场推出时隙的柔性控制方法,旨在将航班到达跑道时间设定在以计划到达跑道时间为基准的特定时间区间范围内,以确保推出时间可满足特定概率条件下的到达跑道时间范围约束。“推出时隙”控制的“柔性”内涵主要体现在机场运行决策人员可为离场活动分配一个可行的推出时间区间,实现可行推出时隙与在计划时间范围内到达跑道概率之间的最佳匹配。
4.1 机会约束条件设置
假设离场航班的概率滑行时间为,计划到达跑道时间为trunway,到达跑道允许提前和延后的最大时间分别为x和y(单位为min),控制允许提前和延后情况发生的概率为p,允许提前和延后的发生概率也可以设置不同的取值。为了根据所需控制到达跑道的时间范围计算获得推出时间范围,采用随机规划理论构建式(8)和式(9)所示的机会约束条件。
机会约束式(8)表示trunway之前x内到达跑道的概率大于或等于p,约束式(9)表示trunway之后y内到达跑道的概率大于或等于p。
4.2 可行推出时隙界定
相比于3.1节中计算的航班提前到达跑道头的概率,机会约束式(8)和式(9)可同时控制航班在计划时间前后某一特定时间范围内到达跑道头的概率,根据这2个约束可计算出满足所设置的最大允许提前时间x、最大允许延误时间y以及位于允许时间范围内的最小概率p下的可行推出时间范围。
将式(8)和式(9)2个机会约束条件转化为确定性的约束条件式(10)和式(11):
式中:表示概率滑行时间累积分布函数的反函数,根据式(10)和式(11),可计算出推出时间的可行区间范围,tpush∈[trunway-x-Φ-1f(1-p),trunway+y-Φ-1f(1-p)],这个时间范围即为建议的“推出时隙” 。
4.3 推出时隙计算实例
基于第2节得到的概率滑行时间预测结果,采用4.1节和4.2节中的方法计算离场航班的可行推出时隙。将计划到达跑道时间的最大允许提前量x和最大允许延误量y均设置为3 min,提前/延后时间不超过x/y到达跑道的概率p均设置为90%,选取一天中不同时段的航班求解得到的可行推出时隙如表6所示,各个时段选取的航班相应的概率滑行时间如图6所示。与第3节的推出时间计算方法相比,本节计算得到的推出时间不是一个刚性时间,而是一个可行的推出时隙。在机场实际运行过程中,推出时隙可为管制员科学合理控制离场航班推出过程提供更多的灵活性。

图6 各时段选取航班的概率滑行时间Fig.6 Probabilistic distribution of taxiing time for selected flight in each time period

表6 不同时段航班可行推出时隙Table 6 Feasible pushback time slots for flights in different time periods
计算结果表明,每架航班的推出时隙与其预测滑行时间的概率分布有关:滑行时间的不确定性越大,相应的可行推出时隙越小,此类情景下航班推出时间控制的灵活性较低,仅可在有限范围内才能使到达跑道的时间范围满足预先设置的概率水平;反之,滑行时间的不确定性越小,相应的可行推出时隙越大,此类情景下航班推出时间控制的灵活性较高,可在较大范围内确保到达跑道的时间范围满足预先设置的概率水平。
5 结论
本文研究了基于概率滑行时间的航空器离场推出柔性控制问题,并选取昆明长水机场为实例对所提方法进行了验证。主要结论如下:
1)构建了基于随机森林回归算法与核密度估计方法相结合的概率滑行时间预测模型,分析了单架航班滑行时间的不确定性,提出的6个概率预测性能指标的计算结果表明滑行时间预测结果的均值接近真实滑行时间的百分率超过70%,相比基于随机森林回归等确定性预测方法,所提预测方法不仅可对滑行时间本身进行预测,亦可量化分析每架航班预测滑行时间的不确定性。
2)基于概率滑行时间的分布特性,针对推出“时刻”和“时隙”2个视角,分别提出了基于缓冲区的离场推出时刻柔性控制方法、基于机会约束的离场推出时隙柔性控制方法,所提方法可有效促进传统推出控制刚性约束向多视角柔性控制的灵活转化。其中,推出“时刻”柔性控制方法通过对缓冲区长度进行最优设置,实现了离场滑行时间与到达跑道头概率之间的最优权衡,解决了所有离场航班采用统一的缓冲区时间所导致的运行低效问题;推出“时隙”柔性控制方法通过控制可行推出时隙,实现离场推出时隙长度与在计划时间范围内到达跑道概率之间的最佳匹配,有助于提高推出时间策略的鲁棒性,以及策略执行的灵活度,减少推出时间二次分配的发生频率。
3)离场航班推出时隙与其预测滑行时间的概率分布具有明显的相关性,通过降低滑行时间预测的不确定性,可得到更大的可行推出时隙,进而提高航班推出时间控制的灵活性和可执行性,增强机场管制人员对推出控制方案的接受度。

