一种无人机-无人车编队系统容错控制方法

马亚杰，王娟，姜斌，龚建业

南京航空航天大学 自动化学院，南京 211106

随着控制系统的复杂化和控制任务的多样化，仅依靠单个智能体很难实现现代任务的要求和目标。受生物集群现象启发［1］，学者们提出了多智能体系统（Multi-Agent System， MAS）的概念。由于更高的自治性、更强的稳定性和更好的适应性，多智能体系统受到广泛关注。目前，多智能体系统研究领域已取得丰硕理论成果并在工程实践中得到推广应用。其中，一致性实现具有典型的聚集行为特征，已成为研究热点，如无线传感网络［2］、机器人编队［3］、电网同步控制［4］和多机械手协同装配［5］等。由于恶劣工作环境、外部扰动攻击和通信能力受限等，多智能体系统易发生故障且故障极易在系统中传播。按照故障发生位置及传播方式，可以将多智能体系统故障分为3 种类型：个体执行器故障、个体传感器故障及通信链路故障。目前，关于多智能体系统在执行器故障和传感器故障下的容错一致性研究已取得了一定成果［6-7］，而针对通信链路故障问题研究的较少［8］。但是，各智能体之间通过通信拓扑进行信息交互，若发生通信链路故障，极有可能造成邻接智能体状态的不确定，从而增加控制器设计难度，进而影响系统一致性实现。

目前对于通信链路故障的研究还较少，并且主要针对同构多智能体系统。文献［9］针对一般二阶多智能体系统，结合无通信时延情况，利用特征方程根与时延参数之间的关系，得到了通信时延下实现同构多智能体系统一致性的充要条件；文献［10］针对二阶交流微电网，研究其在加性通信链路故障下的适应性问题，设计自适应观测器以实现通信恢复能力，在二阶控制算法作用下可实现对微电网在通信故障下的控制；文献［11］基于齐次性原理设计分布式有限时间观测器，并结合高增益法设计控制器，可以实现在通信链路故障下刚性航天器的姿态跟踪控制。通过文献调研可以发现，关于异构多智能体系统在通信链路故障下的容错编队控制研究还存在大量空白。

由于异构多智能体系统存在不可忽视的个体差异性，相较于同构多智能体系统［12-18］，异构多智能体系统具有不同的系统状态维数和系统参数，因此，其协同控制方案的设计更加有难度，研究成果也较少［19-21］。本文所考虑的多无人机-多无人车编队系统为典型的异构多智能体系统，无人机具有较宽阔的视野，而无人车具有较快的任务执行速度，可以应用在协同监视、防控和侦查等方面，受到研究人员的广泛关注。文献［22］将无人机（Unmanned Aerial Vehicle， UAV）和无人车（Unmanned Grand Vehicle， UGV）系统模型转化为二阶非线性模型，并基于径向基函数神经网络，实现了系统在执行器故障下的容错一致性；文献［23］将异构无人机和无人车系统模型统一为二阶线性模型，并设计了基于反步法的分散式时变编队控制器。可以发现，多无人机-多无人车编队系统的控制研究还处在起步阶段，而通信链路故障会导致通信拓扑Laplacian 矩阵时变，并与无人机和无人车系统参数耦合，大大增加系统控制难度，在以往的研究中尚未考虑。

基于以上分析，本文针对由无人机和无人车组成的异构多智能体系统，研究其在加性通信链路故障下的容错编队控制问题。首先，将四旋翼无人机控制系统模型和两轮驱动式无人车控制系统模型转化，得到转化后的系统；然后，针对多无人机-多无人车编队系统坐标轴OXY二维位置子系统模型设计分布式自适应观测器以实现在通信链路故障下对虚拟领导者状态的观测；最后基于反步法分别设计多无人机-多无人车编队系统坐标轴OXY二维位置子系统及无人机坐标轴Z轴高度子系统控制器，实现通信链路故障下系统容错编队跟踪。本文的主要创新点包括：① 研究对象为由无人机和无人车组成的异构多智能体系统，异构多智能体系统具有不同的系统状态维数和系统参数，并且研究领域目前相对空白；② 研究问题为通信链路故障下异构多智能体系统的容错编队跟踪控制问题，通信链路故障在以往的多智能体系统研究中鲜少考虑，而此类故障对系统的安全运行至关重要；③ 本文基于分布式自适应观测器和反步法设计容错编队控制算法，方法简单且可行性高。

1 预备知识和问题描述

1.1 图论知识

令G=(P，Q，A)表示一个包含N个节点的加权有向图，其中P={p1，p2，…，pN}表示图G的节点集，Q⊆P×P表示边集，图G的邻接矩阵为A=(aij)N×N。定 义(pj，pi)∈Q(i，j=1，2，…，N)表示存在一条从节点pj到节点pi的边，当且仅当(pj，pi)∈Q 时aij≥0，否则aij= 0。定义为 节 点pi的 入 度 ，B=diag{b1，b2，…，bN}∈RN×N为系统入度矩阵，图G的拉普拉斯矩阵为L=B-A。如果图G中存在一个节点与其他节点都存在有向通信，则称图G中包含一个以该节点为根节点的生成树。假定图G中存在一个为其他节点提供参考信号的节点p0，定义G=diag{g1，g2，…，gN}，若 节 点pi(i=1，2，…，N)可以获得节点p0的参考信息，则gi=1，否则，gi=0。

1.2 问题描述

本节首先给出无人机控制系统模型及无人车控制系统模型；然后，对其转化得到多无人机-多无人车编队系统OXY二维位置子系统模型及无人机系统Z轴高度子系统模型；接着，给出通信链路故障模型；最后，给出本文的控制目标。

1.2.1 无人机控制系统模型

图1 给出了第i架四旋翼无人机控制系统模型。其中和分别表示前后左右4 个螺旋桨产生的升力；B={xb，yb，zb}表示机身坐标系；E={xe，ye，ze}表示惯性坐标系。令pi=[pxi，pyi，pzi]T为无人机在惯性坐标系中的坐标，第i架四旋翼无人机控制系统的位置动力学模型为

图1 四旋翼无人机模型Fig.1 Quadrotor UAV model

式中：pxi、pyi与pzi分别表示无人机在惯性坐标系x轴、y轴与z轴中的坐标；φi、θi与ψi分别为无人机在机身坐标系中的滚转角俯仰角与偏航角；Mai表示第i架无人机的质量；g表示重力加速度；为无人机位置系统控制推力。

由于四旋翼无人机的动力学可分为位置动力学和姿态动力学，并且位置动力学比姿态动力学具有更大的时间常数，四旋翼无人机的控制可以用内环/外环结构来实现。在本文中，无人机系统的编队控制问题只涉及位置和速度。因此，在实现多无人机-多无人车编队系统编队构型时暂仅考虑无人机位置系统，无人机位置动力学模型式（1）可以表示为

1.2.2 无人车控制系统模型

图2 给出了第i辆两轮驱动式无人车模型。其中，ri表示驱动轮的半径；Li表示两轮中点到无人车头结点的距离；di表示两轮间距的1/2，θi表示无人车的方向角；pi=[pxi，pyi]T表示两轮中点的坐标表示头结点坐标。

图2 两轮驱动式无人车模型Fig.2 Two-wheeled mobile UGV model

第i辆两轮驱动式无人车的数学模型为

式中：Vi和ωi分别表示线速度和角速度；Mgi和Jgi分别表示无人车的质量和转动惯量；ζi和τi分别表示无人车的力和力矩。

对式（4）求二阶导，并将式（3）代入，可得第i辆两轮驱动式无人车控制系统的动力学模型为

1.2.3 多无人机-多无人车编队控制系统模型

考虑由M辆两轮驱动式无人车和N-M架四旋翼无人机组成的多无人机-多无人车异构编队系统，即使是在上述对无人机和无人车进行模型转化后，仍存在着维数不同的问题：无人机动态系统维数为三维模型，而无人车为二维。为解决上述问题，本文考虑按照惯性坐标系将无人机动力学模型解耦，建立多无人机-多无人车编队系统坐标轴OXY二维位置系统模型，并单独控制无人机系统坐标轴Z轴高度系统模型。

转化得到的坐标轴OXY二维位置系统模型为

式中：xi、vi、ui∈R2分别表示系统中第i个智能体的位置信号、速度信号和控制输入。

无人机系统坐标轴Z轴高度系统模型为

式中：pi、qi、uzi∈R分别表示无人机高度子系统的高度信号、速度信号和控制输入。

本文考虑基于“虚拟领导者-跟随者”实现多无人机-多无人车编队系统坐标轴OXY二维位置系统的编队跟踪，虚拟领导者设计为

式中：x0、v0、u0∈R2分别表示虚拟领导者的位置信号、速度信号和控制输入。由于无人机高度子系统可以解耦单独控制，因此为无人机Z轴子系统式（7）设置期望高度信号pd和期望速度信号qd。

假设1系统拓扑为包含一个以虚拟领导者为根节点的生成树的有向图。

引理1［24］若多智能体系统的拓扑为含有以领导者为根节点的生成树的有向图，则存在一个正定对角矩阵Q能够满足QLG+LGTQ=P，其中，P正定，LG=L+G。

假设2虚拟领导者的控制输入未知但有界，即存在使得其中为未知有界常数。

1.2.4 通信链路故障模型

本文考虑有向图G的通信链路中存在未知加性故障。将通信链路故障下的连接权重(t)和表示为

式中：aij和gi为在未发生通信链路故障情况下的通信拓扑图中的连接权重；(t)和(t)为未知的通信链路加性故障。

注释1如文献［25］所示，在多智能体系统的通信网络中，故障模型式（9）是一种常见的通信链路故障类型。例如，未知的加性链路故障(t)和(t)可以建模为一组网络攻击，攻击者可以侵入信息交互通道并篡改智能体之间的交互信息，这种类型的通信链路故障具有较高的隐蔽性；另外，未知的损坏权重(t)和(t)还可以表示由于任务环境的变化而导致的通信通道信号的衰落。

若发生如式（9）所示的通信链路故障，则将会造成系统通信拓扑图未知且Laplacian 矩阵时变。多智能体系统编队控制设计与系统拓扑结构有关，若系统拓扑发生故障，则控制方案设计难度将大大提高。因此，有效的多智能体系统通信链路故障下的容错编队控制算法设计十分必要。

假设3通信链路故障(t)和(t)有界，它们的导数)和也有界。

假设4连接权重aˉij(t)的正负性和aij相同，的正负性和gi相同。

注释2假设4 可以保证在发生通信链路故障后，系统拓扑结构的连通性与原系统拓扑连通性相同。

1.2.5 控制目标

针对通信链路故障下的多无人机-多无人车编队系统，本文提出自适应容错控制策略，保证系统在故障下的稳定性和实现多无人机-多无人车编队系统坐标轴OXY二维模型编队跟踪及无人机系统高度一致性。

若式（10）成立，则可以认为多无人机-多无人车编队系统坐标轴OXY二维模型实现编队跟踪控制：

式中：ρxi(t)∈R2和ρvi(t)∈R2表示已知的编队构型向量，并且满足ρ̇xi(t)=ρvi(t)。

若式（11）成立，则可以认为无人机系统实现高度一致性控制：

2 自适应容错编队控制设计

针对多无人机-多无人车编队系统通信链路故障下的容错编队问题，本节基于分布式自适应观测器和反步法，分别针对多无人机-多无人车编队系统坐标轴OXY二维位置系统和无人机系统坐标轴Z轴高度系统设计控制器，并证明所设计的控制器的可行性和有效性。

2.1 二维位置子系统自适应容错编队控制设计

本节针对多无人机-多无人车编队系统坐标轴OXY二维位置系统，首先设计分布式自适应观测器以观测虚拟领导者状态，然后基于反步法设计控制律实现系统编队跟踪，最后完成性能分析。

2.1.1 分布式自适应观测器设计

引理2在假设1、假设3 和假设4 均成立的情况下，存在一个对称正定矩阵Q(t)可以满足引理1，且Q(t)及其导数均有界。

式中：对角元素选取为

当选取如式（12）所示的Q(t)时，不难证明该正定对角矩阵满足引理1。下证Q(t)及其导数有界。均有界，因此，矩阵有界，由此证明矩阵

在假设3成立的情况下，矩阵LG(t)及其导数Q(t)的有界性。对式（13）求导，可以得到：

不难发现，̇(t)也有界，因此矩阵Q(t)的导数也有界。证毕。

进一步，由于领导者状态不可测，需为每一个跟随者智能体i(i=1，2，…，N)设计分布式领导者状态观测器和，并定义观测误差=-x0和=-v0。然而，在本文中，只有邻居智能体的信息可以用于跟随者智能体i的控制器设计中，因此，定义邻域观测误差为

假设5假设分布式领导者状态观测误差ξ1i和ξ2i已知并可用于控制器设计。

注释3虽然在分布式领导者状态观测误差ξ1i和ξ2i中存在未知项(t)和(t)，但由文献［26］可知，可以假设误差项ξ1i和ξ2i可测量并可用于分布式控制器设计。

定义全局误差向量：

由式（16）可知，当智能体i的邻域误差ξ1i和ξ2i收敛到零时，其观测误差和也能收敛到0。

若假设1～假设5 成立，可以得到定理1。

定理1在假设1～假设5 成立的情况下，设计领导者状态观测器为

式中：

且对于∀i∈{1， 2，…，N}，初始值c1i(0)和c2i(0)均＞1为对虚拟领导者的控制输入界值的估计且和为符号函数，

若设计式（17）所示的分布式领导者状态观测 器 ，则 观 测 误 差和

证明根据式（8）和式（17），可以得到

选择如式（20）所示的正定李雅普诺夫函数：

式中：γξ1＞0 和γξ2＞0 为常数并在之后的设计中给出

对式（20）求导，可以得到Vξ的时间导数为

根据引理1 和引理2，并将式（19）代入到式（21）中，可以得到

利用Young 不等式对式（23）中相关项放缩，可以得到

将式（24） ～式（ 32）代入式（23）中，可以得到

式中：

式（34）表明：ξ1i、ξ2i、c1i、c2i和在通信链路故障下仍能实现最终有界。

对式（34）进行求解，可以得到

由式（35）可得

注释4定理1 仅在假设3 成立的情况下才能成立。反之，若不满足假设3，即仅有通信链路故障和有界（它们的导数不满足有界条件），则式（21）中和可能无界，会导致式（33）和式（34）不成立，无法进行性能分析。

2.1.2 容错编队控制设计及性能分析

在分布式自适应观测器设计的基础上，进一步进行容错编队控制器设计，定义误差变量和根据式（6）和式（17）可以得到误差变量exi和evi的误差动力学方程为

考虑针对多无人机-多无人车编队系统坐标轴OXY二维位置系统误差动力学方程式（37）和式（38）采用基于反步法设计控制算法。假定evi为式（37）的输入信号。定义虚拟控制输入信号αi，当evi=αi时，需要保证limt→∞exi(t)=0 成立。

虚拟控制输入信号αi设计具体如式（39）所示：

式中：k1i＞0 为控制增益。

虚拟跟踪误差为

则可以得到引理3。

引理3如果则可以推导得到limt→∞exi(t)=0。

证明选择如式（41）所示的李雅普诺夫函数：

对式（41）求导，并将式（37）代入，可以得到

将式（39）中设计的虚拟控制输入信号αi代入到式（42）中可得

下面设计系统实际控制输入信号ui来使得虚拟控制信号跟踪误差的导数为

式中：虚拟控制变量αi的导数为

设计如式（46）所示的控制律：

式中：k2i＞0 为控制增益。

定理2针对多无人机-多无人车二维位置子系统式（6），在设计有如式（17）所示的分布式自适应观测器的基础上，在式（46）所示的控制器的作用下能够保证多无人机-多无人车坐标轴OXY二维位置子系统保持稳定且实现其容错编队控制，即及

证明选择如式（47）所示的李雅普诺夫函数：

结合式（43），并将式（46）所示的控制信号ui代入上式，可以得到V2关于时间的导数为

因为V2≥0，由式（48）可以得到

2.2 无人机系统坐标轴Z 轴高度子系统跟踪控制设计

式中：i=M+1，M+2，…，N。

式中：k1i＞0 为控制增益。

首先，分析αi的性能，定义跟踪误差为

选择如式（54）所示的李雅普诺夫函数为

对式（54）求导，并将式（50）和式（52）代入，可以得到

设计如式（56）所示的控制律：

式中：k2i＞0 为控制增益。

定理3在控制律式（56）的作用下，无人机坐标轴Z轴高度系统能实现二阶一致性，即

证明选择如式（57）所示的李雅普诺夫函数：

对式（57）求导，可以得到

因为V2i＞0，由式（58）可以得到

注释5在分布式容错编队控制设计中，所考虑的研究对象多无人机-多无人车编队系统本身是一类异构多智能体系统，对其直接进行协同编队控制器设计是十分困难的。因此，为了处理无人机与无人车系统的异构问题，我们通过坐标转换，将四旋翼无人机系统与两轮驱动式无人车系统转化成如式（6）所示的无人机-无人车编队控制系统，并且无人机系统的实际上升推力是需要通过相反的转换得到。另一方面，本文的主要贡献是针对具有通信链路故障的多无人机-多无人车系统，解决了容错编队跟踪控制问题，使得在通信链路故障下无人机-无人车位置子系统能够跟踪虚拟领导者的动态轨迹并形成期望的编队构型，同时无人机高度子系统跟踪期望的高度。

注释6在对无人机坐标轴Z轴高度子系统控制时，不涉及系统通信拓扑，因此无需考虑通信链路故障的影响。若无人机需通过与邻接无人机信息相互才能获得期望信号，则在控制器设计时需考虑到通信链路故障的影响，可参考2.1 节设计方法针对无人机系统高度子系统进行控制器设计。

注释7为了便于分布式容错编队控制设计，2.1 与2.2 节中的容错编队控制设计过程中将无人机和无人车作为质点来设计，所设计的控制信号ui和uzi是经过转换的多无人机-多无人车编队控制系统模型式（6）和式（7）的控制输入。而在实际的物理模型中，无人机位置系统的控制输入为4 个螺旋桨产生的总上升推力，因此，通过逆变换，可以得到无人机控制推力=同样的，可以得到无人车控制力和力矩

3 仿真分析

本节将设计的控制方案应用到多无人机-多无人车编队系统中，仿真验证了所提控制方案的可行性和有效性。

3.1 仿真条件

多无人机-多无人车编队系统由3 架四旋翼无人机和3 辆两轮驱动式无人车组成。系统的通信拓扑如图3 所示，其中智能体1、2 和3 为两轮驱动式无人车，智能体4、5 和6 为四旋翼无人机。

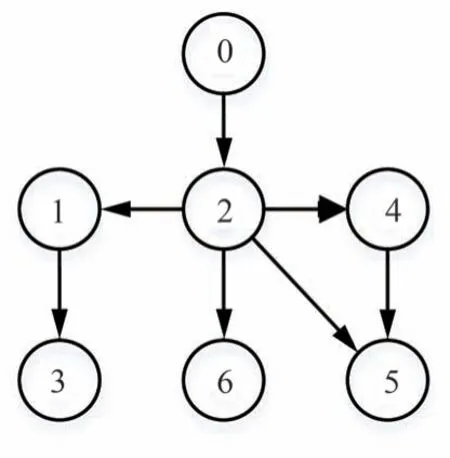
图3 通信拓扑图Fig.3 Communication topology

根据文献［23］，选取无人机和无人车的物理参数为：Mai=2 kg，Li=0.5 m，Mgi=23 kg，Jgi=1。考虑多无人机-多无人车编队系统通信链路故障为

其余通信拓扑图中连接权重保持不变。虚拟领导者的初始状态设置为：x0(0)=[0.1， 0.1]T，v0(0)=[0.01， 0.2]T，虚拟领导者输入u0(t)=[0， -0.25sin(0.5t)]T。多无人机-多无人车编队系统二维位置系统初始状态定义为

设置变量c1i和c2i的初值为：c11(0)=1.5，c21(0)=1.5；c12(0)=1.5，c22(0)=1.4；c13(0)=1，c23(0)=1；c14(0)=1.5，c24(0)=1.5；c15(0)=1.3，c25(0)=1.5；c16(0)=1.5，c26(0)=1.5。

定义坐标轴Z轴模型期望高度pd=5 和期望速度qd=0，设置无人机系统坐标轴Z轴模型初始状态为：p4(0)=2，q4(0)=-3；p5(0)=2.4，q5(0)=2；p6(0)=3，q6(0)=2。

3.2 仿真结果

仿真结果如图4～图12 所示。图4 和图5 分别为跟随者无人机和无人车在三维和二维空间的运动轨迹图。从图中可以看出，跟随者无人机和无人车在通信链路故障的影响下依然能够有效地跟踪领导者的运动轨迹，并且形成期望的三角形编队构型。图6 为多无人机-多无人车编队系统位置观测误差图。从图中可以看出，在t＞10 s 时，系统发生通信链路故障，连接权重a31和a42遭遇通信故障影响发生改变，智能体3 和智能体4 观测误差曲线出现抖动，智能体4 对故障更为敏感，但在分布式自适应观测器式（17）的作用下，抖动很快消失。因此，在观测器的作用下，多无人机-多无人车编队系统能够准确观测虚拟领导者状态并对通信链路故障具有较好的鲁棒性。

图4 无人机与无人车三维运动轨迹Fig.4 Three-dimensional trajectories of UAVs and UGVs

图5 无人机与无人车二维运动轨迹Fig.5 Two-dimensional trajectories of UAVs and UGVs

图6 无人机-无人车编队系统位置邻域观测误差ξ1iFig.6 Position neighborhood observed errors ξ1i of UAVs-UGVs system

在仿真过程中，选取控制增益k1i=4 和k2i=3。图7 为多无人机-多无人车编队系统位置跟踪误差。从图7 中可以看出，在t＞10 s 时，系统的编队跟踪性能受到通信链路故障的影响，智能体4 对故障较为敏感，编队跟踪误差曲线出现轻微抖动，但在容错编队控制器式（46）的基础上，抖动很快消失，因此，多无人机-多无人车编队系统在通信链路故障影响下依然能够保持良好的编队跟踪性能。图8 为未加容错编队控制器的情况下，多无人机-多无人车编队系统的位置编队跟踪误差曲线图。从图中可以看出，在t＞10s时，编队跟踪误差不能收敛到0，因此，系统不能保持期望的编队性能。图9 和图10 分别为无人机系统坐标轴Z轴位置一致性跟踪误差和速度一致性跟踪误差。从这2 张图中可以看出，在独立设计的无人机系统坐标轴Z轴模型控制信号式（56）的作用下，可以实现无人机系统坐标轴Z轴模型一致性。图11 给出了跟随者无人车的控制力ζi和力矩τi曲线。图12 给出了跟随者无人机位置系统的控制推力的曲线。

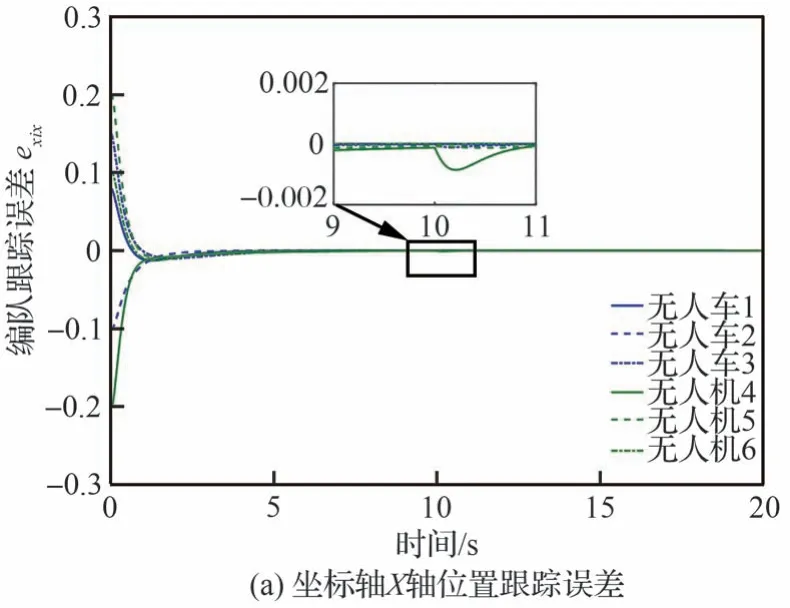
图7 无人机-无人车编队系统位置跟踪误差exiFig.7 Position tracking errors exi of UAVs-UGVs system

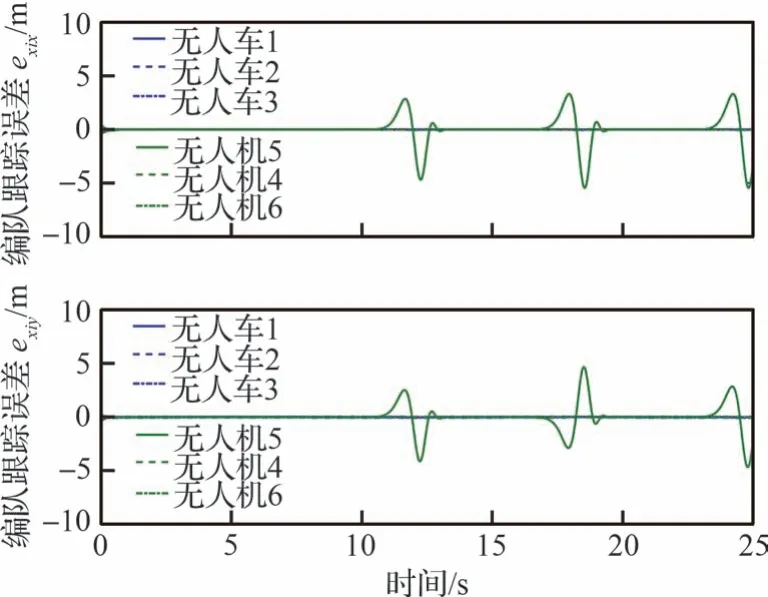
图8 无容错控制器下无人机-无人车编队系统位置跟踪误差Fig.8 Position tracking errors of UAVs-UGVs system without proposed fault-tolerant scheme

图9 无人机高度系统位置跟踪误差p͂iFig.9 Position tracking errors p͂i of altitude systems of UAVs

图10 无人机高度系统速度跟踪误差q͂iFig.10 Velocity tracking errors q͂i of altitude systems of UAVs

图11 跟随者无人车控制力ζi 与力矩τiFig.11 Control force ζi and control torque τi of follower UGVs

图12 跟随者无人机控制推力U1iFig.12 Control thrust U1i of follower UAVs

根据仿真分析，可以得出如下结论：在设计的分布式容错控制方案下，可以实现多无人机-多无人车编队系统通信链路故障下的编队跟踪。

4 结 论

针对由四旋翼无人机和两轮驱动式无人车组成的异构多无人机-多无人车编队系统，本文研究其在通信链路故障下的容错编队控制问题。首先建立了多无人机-多无人车编队控制系统模型；基于邻接智能体的局部信息设计分布式自适应观测器，实现了在通信链路故障下多无人机-多无人车编队控制系统对虚拟领导者状态的观测，并进一步设计了容错编队控制器，保证了系统的稳定性和编队跟踪性能。仿真结果验证了所设计的观测器和控制器的有效性。后续将研究通信链路故障导致拓扑结构连通性发生变化时的异构无人机-无人车编队系统的编队控制问题。