布尔控制网络的能观测性综合问题

谢壹冬，陈晓艳，韩晓光

(天津科技大学电子信息与自动化学院，天津 300222)

1969年，Kauffman首次提出了布尔网络[1]的概念，用此概念描述蛋白质或基因间的逻辑行为和联系.布尔网络采用数值“0”(非激活的)或“1”(激活的)对其状态节点进行量化，使用逻辑函数表征基因之间的相互作用，并且每个状态节点依靠逻辑函数更新其值.至今，布尔网络已经被广泛应用于诸多实际问题，如细胞分化[2]、免疫应答[3]、三神经元网络[4]及其他领域[5].布尔网络在施加外部输入和系统输出后，能够扩展为布尔控制网络[6].

在2001年，程代展研究员提出了矩阵半张量积(semi-tensor product of matrices，STP)[7]的概念，这是一种新的矩阵乘积，它将矩阵的普通乘法扩展到任意两个矩阵，使矩阵技术更易于应用到逻辑函数、高维数组和非线性系统等问题.STP理论已成功应用于布尔控制网络研究中.利用STP技术，一个布尔控制网络的逻辑行为可等价表示为双线性方程的形式.基于该双线性方程，布尔控制网络的一些动态性质得到深入研究，如能控性[8]、能观测性[8-11]、可探测性(也称可重构性)[11]及其他性质[12].

能观测性是布尔控制网络的一个基本性质，4种不同类型的能观测性概念在文献[8-11]中被相继提出.能观测性描述了是否可以通过输入-输出值确定一个系统的初始状态.Zhang等[13]基于加权对图和有限状态自动机的方法设计了一种有效算法，用以验证4种类型的能观测性.当一个系统不具有能观测性时，研究能观测性综合问题具有重要意义.为此，Zhang[14]开启了布尔控制网络能观测性综合问题的研究，证明了状态反馈有时能够增强任意实验能观测性[11]，并给出了这种类型能观测性的标准状态反馈控制器的设计算法.本文关注的是多实验能观测性[10]，研究了标准状态反馈控制器和带有外部输入的状态反馈控制器对这种类型能观测性的影响.

1 预备知识

1.1 基本符号

(1)N：自然数集；

(2)Z+：正整数集；

(3)R：实数集；

(4)Rn×m：n×m维实矩阵集合；

(5)Col(B)：矩阵B的列向量构成的集合；

(6)D：由0和1组成的集合，即D={0,1}；

(7)[n,m]：{n,n+1,…,m}，其中n,m∈N，n≤m；

(8)：单位矩阵In的第i列；

(9)1n=；

(10)Δn={|i=1,2,…,n}；

(11)若矩阵B∈Rn×m满足Col(B)∈Δn，则称其为一个逻辑矩阵.方便起见，简记为，其中ik∈[1,n]，1≤k≤m；

(12)Ln×m：n×m维逻辑矩阵集合.

1.2 矩阵半张量积

设矩阵B∈Rm×n，C∈Rp×q，s为n与p的最小公倍数，则矩阵B和C的半张量积定义为：BC=(B⊗Is/n)(C ⊗Is/p)，其中⊗表示Kronecker积.特别当n=p时，有BC=BC，因此，普通矩阵乘积是STP的一种特殊情况.方便起见，在下文中常略去符号“”.

本文用到STP的一些基本性质如下：考虑两个列向量X∈Rm×1和Y∈Rn×1，则XX=ΦmX，XY=X⊗Y，YX=W[m,n]XY ，其中设x,y∈Δ2，¬x表示x的逻辑非运算，x∨y表示析取运算，x∧y表示合取运算，x→y表示蕴含运算，即¬x=Mnx ，x∨y=Mdxy ，x∧y=Mcxy ，x→y=Mixy，其中Mn=δ2[2,1]，Md=δ2[1,1,1,2]，Mc=δ2[1,2,2,2]，Mi=δ2[1,2,1,1].关于STP的更多性质详见文献[15].

1.3 布尔控制网络及其代数形式

本文研究具有n个状态节点、m个输入节点和q个输出节点的布尔控制网络，其动态方程表示为

其中xi(t)、yj(t)和uk(t)分别表示t时刻的状态节点、输出节点和输入节点，即xi(t)∈D，yj(t)∈D，uk(t)∈D，t∈N；fi:Dn+m→Dn和hj:Dn→Dq分别表示状态和输出逻辑函数，i∈[1,n]，k∈[1,m].

在STP框架下，方程(1)等价地转换为

1.4 有限状态自动机

一个确定型有限状态自动机(deterministic finitestate automaton，DFA)是一个5元组A=(S,E,σ,s0,F)，其中S表示有限状态集，E表示有限事件集，s0∈S表示初始状态，F⊆S表示最终状态集，σ:S×E→S表示转移函数并且可以扩展为σ:S×E*→S ，E*=.有限状态自动机A生成的语言表示为L(A)={ω∈E*|σ(s0,ω)∈F}.当L(A)=E*时，称有限状态自动机A是完备的.

1.5 能观测性

在文献[13]中，作者证明了布尔控制网络的4种不同类型能观测性概念两两不等价.在文献[14]中，作者讨论了最强类型的能观测性综合问题.本文研究另一种类型的能观测性(称为多实验能观测性)综合问题.

定义1[13]若对于布尔控制网络(2)的任意两个不同初始状态，皆存在一个输入序列，使得对应的输出序列和不相同，则称布尔控制网络(2)是多实验能观测的.

注：在本文表述中，多实验能观测性简称为能观测性.

定义2[13]布尔控制网络(2)的加权对图描述为一个3元组G=(V,E,W)，其中顶点集V×V|存在，使得，或者，加权函数W :E→2ΔM，或者称为一个非对角顶点；否则称其为一个对角顶点，并用记号◇表示.值得注意的是，表示为同一个顶点.

下例说明了如何计算一个给定布尔控制网络的加权对图.

例1考虑布尔控制网络

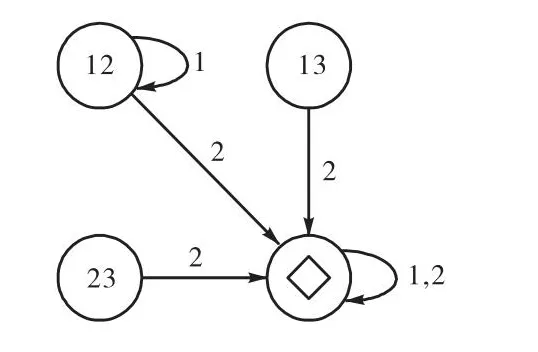
图1 布尔控制网络(3)的加权对图Fig.1 Weighted pair graph of Boolean control network(3)

下面的命题给出了布尔控制网络能观测性的验证方法.

命题1[13]布尔控制网络(2)是不能观测的，当且仅当其加权对图中存在非对角顶点以及由算法1生成对应的DFA是完备的.

算法1[13]一个新的DFA定义为：

(1) 事件集ΔM，初始状态；

(3) 剩余的顶点构成最终状态集.

例2再次考虑布尔控制网络(3)，其加权对图为图1，基于算法1得到每一个非对角顶点对应的DFA，如图2所示.因为是完备的，根据命题1，布尔控制网络(3)是不能观测的.

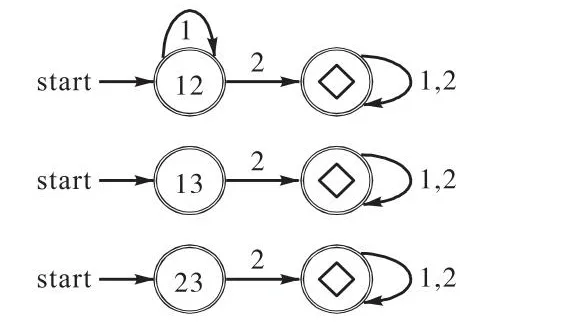
图2 布尔控制网络(3)每一个非对角顶点对应DFAFig.2DFA of each non-diagonal vertex with respect to Boolean control network(3)

1.6 状态反馈控制器

考虑布尔控制网络(2)，带有外部输入的状态反馈控制器定义为

其中v(t)表示外部输入，v(t)∈DP；g:DN+P→DM表示布尔函数，P∈N.借助于STP，控制器(4)可等价转换为

方程(6)进一步表示为

特别当P=1时，带有外部输入的状态反馈控制器变为标准状态反馈控制器，即

在这种情况下，方程(7)简化为

其中gi∈LM×1，i∈[1,N].

2 主要结果

2.1 能观测性综合

在这一小节，研究带有外部输入的状态反馈控制器(5)对布尔控制网络(2)能观测性的影响.事实上，控制器(5)有时可使一个不能观测的布尔控制网络变为能观测的，有时不能；反之，控制器(5)也可以使一个能观测的布尔控制网络变为不能观测的.

首先，下面例子表明了控制器(5)可使一个不能观测的布尔控制网络变为能观测的.

例3由例2可知，布尔控制网络(3)是不能观测的.若选取带有外部输入的状态反馈控制器

将其代入布尔控制网络(3)中，得到闭环系统

闭环系统(10)的加权对图和每一个非对角顶点对应的DFA如图3所示.根据命题1，闭环系统(10)是能观测的.

图3 闭环系统(10)的加权对图和每个DFA Fig.3 Weighted pair graph and each DFA of closed-loop system(10)

其次，下面例子表明了控制器(5)无法使一个不能观测的布尔控制网络变为能观测的.

例4考虑布尔控制网络

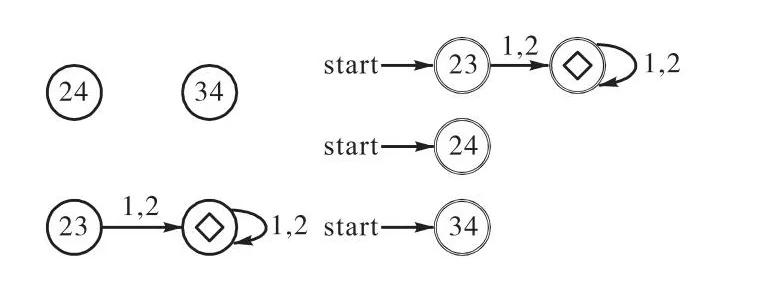
图4 布尔控制网络(11)的加权对图和每个DFA Fig.4 Weighted pair graph and each DFA of Boolean control network(11)

将其代入布尔控制网络(11)中，得到闭环系统

最后，下面例子表明了控制器(5)可使一个能观测的布尔控制网络变为不能观测的.

例5考虑布尔控制网络

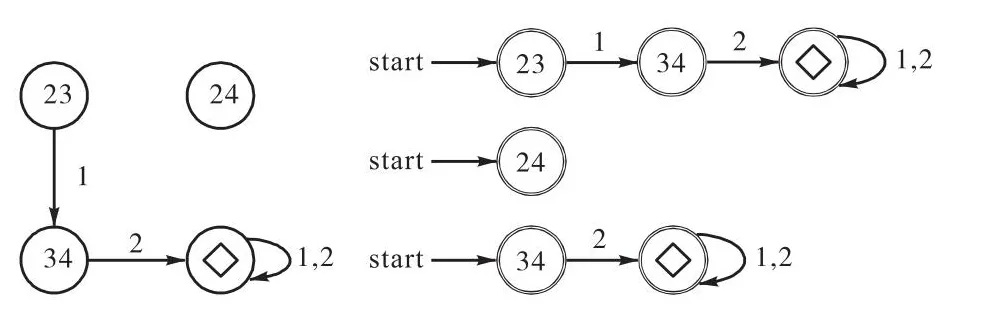
图5 布尔控制网络(13)的加权对图和每个DFA Fig.5Weighted pair graph and each DFA of Boolean control network(13)

将其代入布尔控制网络(13)中，得到闭环系统

2.2 P=1和P＞1状态反馈控制器对能观测性的影响

在文献[14]中，作者证明了对于一个不满足任意实验能观测性的布尔控制网络(2)，若存在带有外部输入的状态反馈控制器(P＞1)使其闭环系统满足这种类型的能观测性，则必然存在标准状态反馈控制器(P=1)使其闭环系统也满足这种类型的能观测性，反之亦然.然而，这两种类型的状态反馈控制器对布尔控制网络的多实验能观测性有不同的影响.

定理1对于不能观测的布尔控制网络(2)，如果存在标准状态反馈控制器使其对应的闭环系统能观测，则一定存在带有外部输入的状态反馈控制器使其对应的闭环系统也能观测，反之不成立.

证明：设布尔控制网络(2)是不能观测的，若存在标准状态反馈控制器使闭环系统(9)能观测，则令Gi=[gi,gi,…,gi]，i∈[1,N].显然带有外部输入的状态反馈控制器也可使闭环系统(7)能观测.反之不成立，详见下例.

例6再次考虑例1所示的布尔控制网络(3).例3表明了存在一个带有外部输入的状态反馈控制器可使布尔控制网络(3)变为能观测的.下面证明不存在标准状态反馈控制器(8)使布尔控制网络(3)变为能观测的.为此，罗列所有标准状态反馈控制器

其中∈Δ2.将控制器(15)代入布尔控制网络(3)，可得所有闭环系统

其中∈.每一个闭环系统的加权对图和每个非对角顶点对应的DFA如图6所示.因此，根据命题1，闭环系统(16)都是不能观测的.

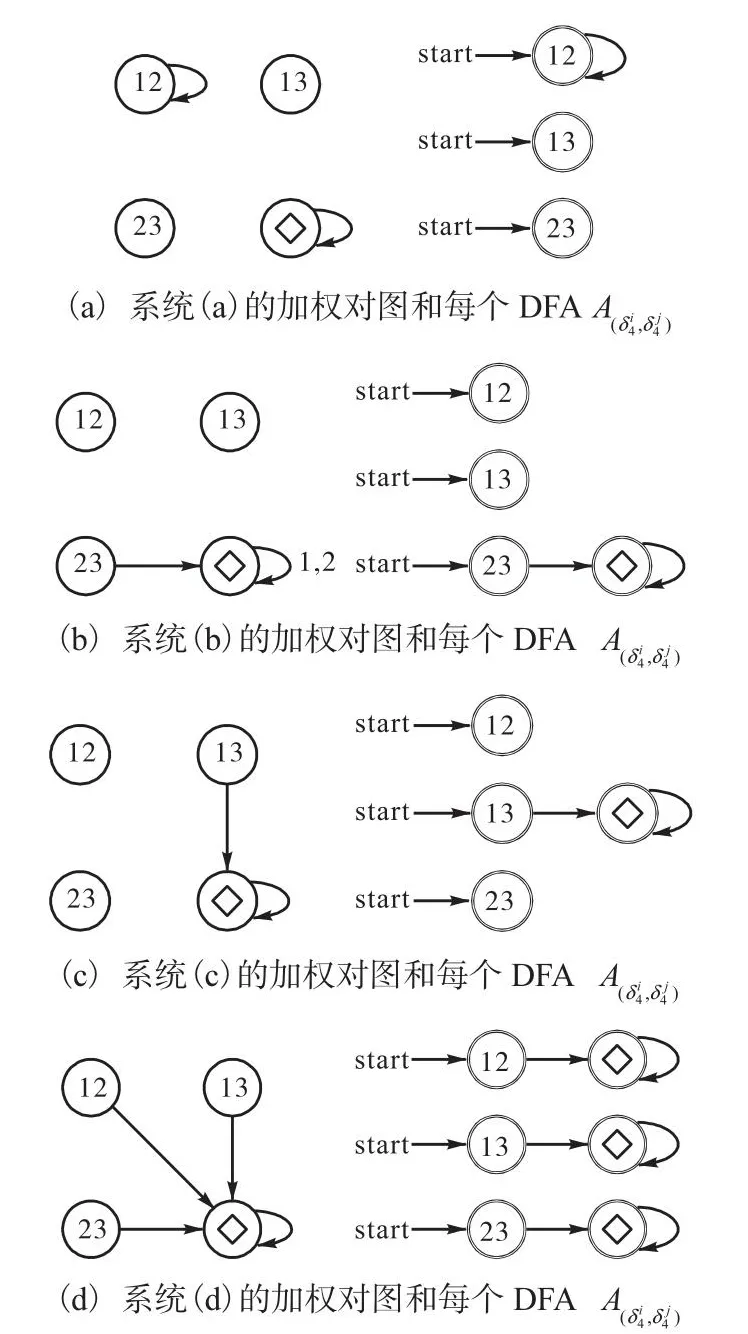
图6 闭环系统(16)中每个系统的加权对图和对应DFAFig.6 Weighted pair graph and corresponding DFA for each system in closed-loop system(16)

3 结 语

本文研究了标准状态反馈控制器和带有外部输入的状态反馈控制器对布尔控制网络多实验能观测性的影响，并证明了如果存在标准状态反馈控制器使一个不能观测的布尔控制网络变为能观测的，则一定存在带有外部输入的状态反馈控制器使一个不能观测的布尔控制网络变为能观测的，反之不成立.此外，本文获得的初步研究结果开启了对布尔控制网络多实验能观测性综合问题的研究.未来工作需要针对一个不能观测的布尔控制网络，设计一个有效算法，寻找使该布尔控制网络变为能观测的所有状态反馈控制器.