τ型的模糊β-覆盖粗糙集模型及其性质①
吴凡, 孔祥智
江南大学 理学院,江苏 无锡 214122
互联网时代中大规模复杂信息的涌现, 带来处理(计算)复杂性的难度增加. 大数据作为继云计算、 物联网之后IT产业又一次重要的技术变革, 正在驱动管理领域的新变革. 粒计算[1]是由美国控制论专家Zadeh提出的智能研究领域中解决复杂问题的新方法和有效工具, 在大数据处理中, 对降低数据规模具有重要研究意义. 信息系统[2](也称为知识表示系统)是粒计算研究中重要的数学模型之一, 它具有属性集和对象集两个维度, 能够描述数据对象的某些属性特征. 模糊信息系统[3]综合了信息系统、 模糊集[4]与粗糙集[5], 逐渐受到人们的关注, 成为一个研究热点. 自文献[6]首次结合模糊集理论和粗糙集理论提出模糊粗糙集概念后, 模糊粗糙集理论由此得到较多研究[7-11]. 文献[12]引入了模糊β-覆盖的概念, 用参数β替换1, 实现了由特殊到一般的转化.
本文基于模糊粗糙集理论, 借助模糊等价关系、 模糊上下近似算子以及互补近似算子的概念, 找出了模糊信息系统的一个约简, 达到了去除模糊信息系统的冗余属性的效果. 文献[13]和文献[14]先后定义了两种模糊β-覆盖粗糙集模型, 并用矩阵来表示上、 下近似算子, 这使得计算机处理大型复杂数据成为可能. 相较早期的模型, 本文提出一种τ型的模糊β-覆盖粗糙集模型, 综合邻域和互补邻域两方面进行分析和解决实际问题, 避免了数据采集、 存储以及约简等过程中产生的误差, 从而进行更完备的信息决策.
1 预备知识

对∀A,B∈F(U), 若对∀x∈U都有A(x)≤B(x), 则称A⊆B.A=B当且仅当A⊆B且B⊆A.
对一族{αi}⊂[0, 1],i∈I,I⊆N+, 记∨i∈Iαi或者∨{αi:i∈I}为{αi:i∈I}的上确界, 记∧i∈Iαi或者∧{αi:i∈I}为{αi:i∈I}的下确界. 给出A,B∈F(U), 对∀x∈U, 称(A∪B)(x)=A(x)∨B(x)为A和B的并, 记作A∪B. 称(A∩B)(x)=A(x)∧B(x)为A和B的交, 记作A∩B. 称Ac(x)=1-A(x)为A的补, 记作Ac.
定义2[11]设U是一个非空有限集合,是U的子集组成的集族. 若∅∉且∪C∈C=U均成立, 则称为U的一个覆盖, 二元组(U,)为一个覆盖近似空间.
定义3[16]设(U,)是一个覆盖近似空间, 若(U,)中Xc记作U-X, 则对∀x∈U,x的邻域Nx和互补邻域Mx分别定义为
Nx=∩{C∈:x∈C}
Mx=∩{Cc: (C∈)∧(x∉C)}
定义4[12]设U是一个论域,={C1,C2, …,Cm}⊆F(U), 且β∈(0, 1]. 若对∀x∈U, 都有则称={C1,C2, …,Cm}是U上的一个模糊β-覆盖, 称(U,)为一个模糊β-覆盖近似空间.
定义5[14]设(U,)是一个模糊β-覆盖近似空间,β∈(0, 1], 其中={C1,C2, …,Cm}. 对∀x∈U,x的模糊β-邻域和模糊互补β-邻域分别定义为
定义6[11]设(U,)是一个模糊β-覆盖近似空间,β∈(0, 1], 且C∈. 若下列两个条件之一成立:
(a) 对∀x∈U, 有C(x)<β;
(b) 对x∈U, 若C(x)≥β, 则存在C′∈-{C}使得C′⊆C且C′(x)≥β.
则称C是的一个β-可约元. 否则, 称C是的一个β-不可约元. 若D⊆,-D是的所有β-可约元组成的集合, 则称D是的约简, 记作Γ().
定义7[11]设(U,)是一个模糊β-覆盖近似空间,β∈(0, 1]. 称是由模糊β-覆盖导出的模糊β-邻域族. 称是由模糊β-覆盖导出的模糊互补β-邻域族.
定义8[11]设1,2是U上的两个模糊β-覆盖,β∈(0, 1].Θβ(1)=Θβ(2)当且仅当Γ(1)=Γ(2).

(a) 对∀u∈[x]f, 有A1(u)≤A2(u);
(b) 对∀u∈[x]f, 有A1(u)≥A2(u).
则称f对于A1和A2是一致的. 对∀x∈U, 若对∀u,v∈[x]f, 都有A1(u)=A1(v), 则称f对A1是相容的.
2 τ型的模糊β-覆盖粗糙集模型及其性质
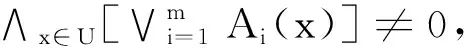

若τ-(X)≠τ+(X), 则称X是τ型的模糊β-覆盖粗糙集, 该模型简称为τ-FβRC.
例1设FIS=(U,AT)是一个模糊信息系统, 其中U={x1,x2,x3,x4,x5,x6}且AT={A1,A2,A3,A4,A5},
令
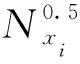
因此, 我们可以计算出X的τ型的模糊β-覆盖的上下近似值为

(i)τ-(Xc)=(τ+(X))c,τ+(Xc)=(τ-(X))c;
(ii)τ+(∅)=∅,τ-(U)=V;
(iii)τ-(X∩Y)=τ-(X)∩τ-(Y),τ+(X∪Y)=τ+(X)∪τ+(Y);
2004年,钟扬帮助西藏大学的琼次仁老师申报国家自然科学基金。此前一年,琼次仁申报的项目没能通过,一度想放弃。“别担心,我们一起想办法。”那段时间,钟扬常常一边插着氧气管,一边连夜修改申请报告。最终,这个项目成为西藏大学拿到的第一个国家自然科学基金项目,极大增强了藏大老师们的科研信心,也加深了藏大老师与钟扬之间的友谊。
(iv)τ-(X∪Y)⊇τ-(X)∪τ-(Y),τ+(X∩Y)⊆τ+(X)∩τ+(Y);
(v) 若X⊆Y, 则τ-(X)⊆τ-(Y),τ+(X)⊆τ+(Y);
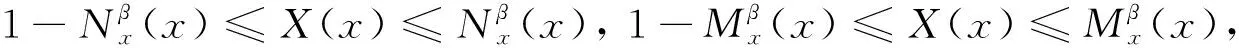
证类似于文献[14]中命题3.1的证明.
为了进一步研究τ-(X)和τ+(X)的性质, 先看如下的一个例子:
例2在例1中, 取
则有
不难看出,
τ-(A)∪τ-(B)≠τ-(A∪B)
τ+(A)∩τ+(B)≠τ+(A∩B)
然而, 定理1(iv)可以在一定条件下成立. 下面结合定义9中映射的一致性与兼容性给出定理1(iv)成立的充分条件:

τ-(X∪Y)=τ-(X)∪τ-(Y)
τ+(X∩Y)=τ+(X)∩τ+(Y)
证根据定理1, 有τ-(X∪Y)⊇τ-(X)∪τ-(Y)和τ+(X∩Y)⊆τ+(X)∩τ+(Y)成立, 下面仅需要证明τ-(X∪Y)⊆τ-(X)∪τ-(Y)和τ+(X∩Y)⊇τ+(X)∩τ+(Y).
对∀y∈V, 若f对X和Y是一致的, 根据定义9可知以下条件之一必成立:
(a) 对∀x∈f-1(y), 有X(x)≤Y(x);
(b) 对∀x∈f-1(y), 有X(x)≥Y(x).
则有
因此τ-(X∪Y)⊆τ-(X)∪τ-(Y)成立.
同样地,
因此τ+(X∩Y)⊇τ+(X)∩τ+(Y)成立. 故定理2成立.
下面将特殊推广到一般情况, 得到以下推论:


(i) 对∀X,Y∈F(U), 若f对X和Y是一致的, 则τ-(X∪Y)=τ-(X)∪τ-(Y)和τ+(X∩Y)=τ+(X)∩τ+(Y)成立;
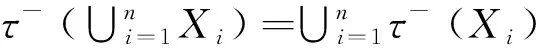
综合定义7、 定义8以及新模型, 并结合可约性与属性约简相关的定理, 得到以下定理:

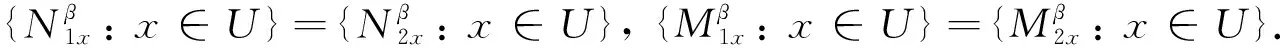
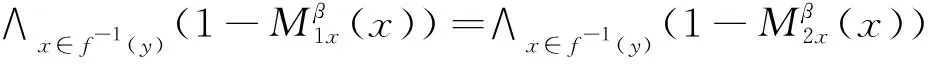
从而
则
可得
从而



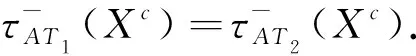

τ-(AT)={τ-(A1),τ-(A2), …,τ-(Am)}
τ+(AT)={τ+(A1),τ+(A2), …,τ+(Am)}

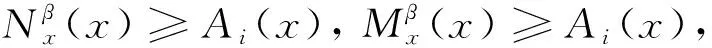
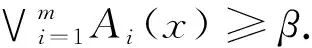
因此τ+(X)={τ+(A1),τ+(A2), …,τ+(Am)}是V的一个模糊β-覆盖.
(ii) 同样地,
因此τ-(X)={τ-(A1),τ-(A2), …,τ-(Am)}是V的一个模糊β-覆盖.

