一种基于Retinex理论改进的低照度图像增强算法

李承铭 陈初侠 柯骏 王佳欣 王世龙 何俊洁

摘要：针对处理低照度图像出现的色彩失真和边缘信息丢失问题，文章基于Retinex理论提出一种改进的低照度图像增强算法。首先，将低照度图像从红、绿、蓝（RGB） 空间转换到色调、饱和度、亮度（HSI） 空间；其次，在HSI空间中只对亮度分量进行处理，这样避免了图像三基色比例关系被破坏；再次，在处理亮度分量时，在Retinex理论的基础上采用双边滤波代替高斯滤波来估算入射图像。实验结果表明，相比于SSR、MSR、MSRCR算法，文章算法增强后的图像避免了色彩失真问题，较好地保留了图像边缘信息。

关键词：Retinex理论；低照度图像；图像增强；HSI

中图分类号：TN391.9    文献标识码：A

文章编号：1009-3044（2023）13-0022-03

开放科学（资源服务）标识码（OSID）

0 引言

视觉是人类感知外部世界的重要生物器官，而图像作为人类获取外界信息的重要载体，传递给人类80%以上的外界信息量[1]。但在现实生活中，由于光线不足等因素导致所获取的图像色彩偏暗，这样的图像不仅影响人们对图像中的信息识别，还极大地降低了图像的后续应用价值。低照度图像增强是图像处理常见问题之一，目的是增强原始图像中的对比度和清晰度，从而得到更高质量的图像。

低照度图像增强方法有很多，有基于直方图均衡化的低照度图像增强[2]、基于色调映射的低照度图像增强[3]、基于暗通道先验的低照度图像增强、基于小波变换的低照度图像增强[4]、基于Retinex理论的低照度图像增强等。本文在研究Retinex理论的基础上，提出了一种改进的低照度图像增强算法，与经典的三种Retinex算法相比，本文算法增强后的图像避免了色彩失真问题，较好地保留了图像边缘信息。

1 Retinex基本理论

1.1 Retinex理论基础

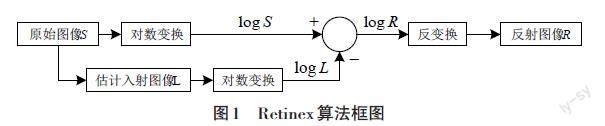
Retinex理論[5]是20世纪70年代由Edwin Land所提出，他认为采集的原始图像S（x， y）是由入射图像L（x， y）和反射图像R（x， y）共同决定，即

[S（x，y）=L（x，y）×R（x，y）]  （1）

Retinex理论的核心是尽可能消除入射分量的影响而最大化估算反射分量。所以准确估算反射图像R（x， y）并提取出来就达到对低照度图像增强的目的。对式（1） 进行对数变换并移位有：

[logR（x，y）=logS（x，y）-logL（x，y）]        （2）

对（2） 式进行反对数变换，可得反射图像R（x， y）为：

[R（x，y）=exp[logS（x，y）-logL（x，y）]]      （3）

Retinex算法框图如图1所示。

1.2  三种Retinex算法

在Retinex理论出现后，相继出现了三种经典的Retinex算法，分别是单尺度Retinex算法（Single Scale Retinex，SSR） 、多尺度Retinex算法（Multi-Scale Retinex，MSR） 和具有色彩恢复的多尺度Retinex算法（Multi-Scale Retinex with Color Restoration，MSRCR） 。

SSR算法在估计入射图像时采用低通滤波器（一般用高斯低通滤波器）和原始图像做卷积来获得，即[L（x，y）=S（x，y）?G（x，y）]，其中“*”是卷积运算符号，G（x， y）是低通滤波函数。最终所得反射图像为

[R（x，y）=exp{logS（x，y）-log[S（x，y）?G（x，y）]}]    （4）

使用SSR算法进行图像增强，当低通滤波函数中尺度调节参数较小时，图像的细节会得到增强但同时会出现较大的色彩失真；当尺度调节参数较大时，图像的色彩能保留较好但图像纹理细节变得模糊。MSR算法是在SSR算法基础上进行多个不同的SSR加权平均得到增强图像。MSR算法较好地解决了SSR算法在增强图像时出现图像纹理细节和颜色保留不可兼顾的缺点，其反射图像为：

[R（x，y）=exp{i=1nwi[logS（x，y）-log（S（x，y）?G（x，y））]}] （5）

式（5） 中，n表示取不同参数的次数，一般取3。[wi]表示第i次滤波所占的比重，它必须满足归一化要求。

尽管MSR算法在SSR算法基础上进行了一些改进，但在对彩色图像进行增强时，MSR算法还是有可能出现图像颜色失真。因为它是对R（红色）分量、G（绿色）分量和B（蓝色）分量分别进行相应的增强运算，这样会打破R、G、B三者之间的比例平衡，从而出现颜色失真。MSRCR算法的出现在一定程度上解决了这一问题。MSRCR算法是在MSR算法基础上引入了颜色恢复函数[γc（x，y）]，是对MSR算法处理后的图像进行再处理，[γc（x，y）]表达式为：

[γc（x，y）=βlnαSc（x，y）c∈（R，G，B）Sc（x，y）]     （6）

式（6） 中，c为颜色通道，b为增益常数，a为非线性强度控制因子。MSRCR增强算法的输出是MSR增强算法的输出[Rc（x，y）]与[γc（x，y）]的乘积。

2  改进的低照度图像增强算法

尽管SSR、MSR和MSRCR三种算法对低照度图像增强具有较好的效果，但实验中发现，采用以上三种算法增强后的图像也存在一些缺陷，主要表现在：1）色彩失真，图像给人一种灰白感；2）图像变得模糊，这是因为Retinex中使用的高斯滤波器不能较好地保留图像的边缘信息。

针对以上两个问题，本文在Retinex算法理论基础上做了针对性的改进。对于色彩失真问题，Retinex算法是对R、G、B三个分量分别进行处理，这样增强的图像很容易出现色彩失真现象。本文采用HSI（色调Hue、饱和度Saturation和亮度Intersity） 色彩空间，而且只对亮度分量进行处理，在增强图像的同时防止了色彩失真现象的出现。在边缘信息保护方面，本文采用双边滤波代替传统的高斯滤波，更好地保护了图像边缘信息。改进算法的框图如图2所示。

3  实验结果与分析

为了验证本文算法的有效性，实验时笔者选取了三幅图像，它们分别是“别墅”“城堡”和“树叶”。如图3、图4、图5所示为原图及四种算法的处理结果。

3.1  主观评价

由图3、图4、图5可得，首先，从图像的明暗程度来看，四种算法处理后的图像都变得更亮。其次，从色彩上看，SSR、MSR、MSRCR算法处理后的图像颜色偏暗，不鲜艳，色彩有较明显的失真；而本文算法处理后的图像颜色亮丽，没有失真现象。再次，从图像的细节看，本文算法处理后的图像更加细腻，边缘部分保护得更好。总之，与SSR、MSR、MSRCR算法相比，本文算法是最优的。

3.2  客观评价

除主观评价外，本文还采用三个客观评价指标进行评判，它们分别是均值、标准差和清晰度。

1）均值。图像均值是整幅图像中所有像素的平均值，它与图像的明暗程度息息相关。图像均值越大，图像显得越亮；反之，图像显得越暗。其计算公式为：

[A=1M×Ni=1Mj=1Nf（i，j）]         （7）

式（7） 中，M和N分别表示图像的行数和列数，f （i， j）表示图像在点（i， j）处的灰度值。

2）标准差。标准差反映了图像像素值与均值的离散程度，图像标准差越大说明图像的质量越好[6]。其公式为：

[σ=1M×Ni=1Mj=1N[f（i，j）-A]2]        （8）

式（8） 中，A为图像的均值。

3）清晰度。图像的清晰度是指人眼视觉感受图像的清晰程度。对一幅图像而言，若其清晰度数值越大，则图像越清晰。其公式表示为：

[Q=1M（N-1）i=1Mj=1N[f（i，j+1）-f（i，j）]2+1（M-1）Ni=1Mj=1N[f（i+1，j）-f（i，j）]2 ] （9）

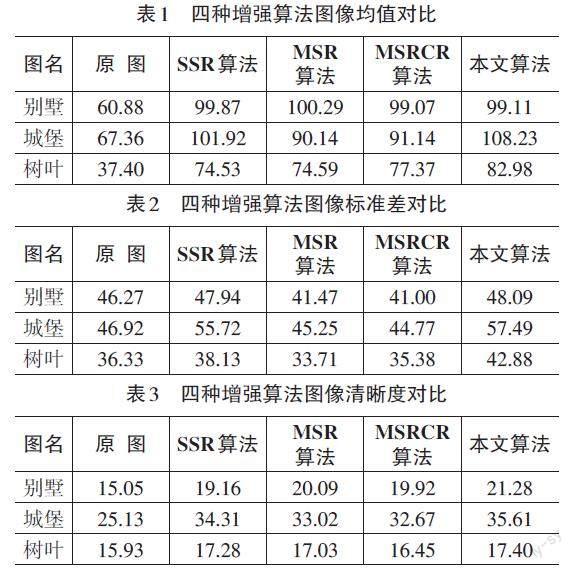
表1、表2、表3分別为三幅图像及四种增强算法的图像均值、标准差和清晰度。从表1可以看出，增强后的图像均值均比原图要大很多，说明四种算法都对低照度图像进行了有效增强，对于“城堡”和“树叶”两幅图，本文算法增强的效果更加明显。从表2可以看出，相较于SSR、MSR、MSRCR算法，本文算法的标准差最大，说明本文算法增强后的图像质量是最好。从表3可以看出，四种算法增强后的图像其清晰度均比原图要好，说明增强后的图像比原图都要清晰；另外，相较于SSR、MSR、MSRCR算法，本文算法增强后的图像其清晰度数值最大，这更进一步地说明本文算法的优越性。

4  结束语

基于Retinex理论本文提出了一种改进的低照度图像增强算法。首先，将低照度图像从RGB空间转换到HSI空间，并只对亮度分量进行处理；其次，处理亮度分量时采用双边滤波代替高斯滤波来估算入射图像。实验结果显示，本文算法在图像均值、标准差和清晰度方面均优于SSR、MSR、MSRCR算法。从图像视觉效果来看，本文算法增强后的图像避免了色彩失真现象，也很好地保留了图像边缘信息。

参考文献：

[1] 杨杰.数字图像处理及MATLAB实现[M].3版.北京：电子工业出版社，2019.

[2] 丁畅，董丽丽，许文海.“直方图”均衡化图像增强技术研究综述[J].计算机工程与应用，2017，53（23）：12-17.

[3] 陈迎春.基于色调映射的快速低照度图像增强[J].计算机工程与应用，2020，56（9）：234-239.

[4] 付争方，朱虹.基于小波变换的低照度图像增强算法[J].山西大学学报（自然科学版），2013，36（4）：497-504.

[5] Land E H，McCann J J.Lightness and retinex theory[J].Journal of the Optical Society of America，1971，61（1）：1-11.

[6] 郭瑞，党建武，沈瑜，等.改进的单尺度Retinex图像去雾算法[J].兰州交通大学学报，2018，37（6）：69-75.

【通联编辑：朱宝贵】