基于并联ResNet-GRU模型的股票价格预测
赵萌 王倩影

摘 要:针对目前股价预测模型在随着网络层数增加而导致梯度发生极端变化的问题,提出一种并联残差神经网络(ResNet)和门控循环单元(GRU)网络模型对股票数据的收盘价进行预测。在沪深300股票价格数据上的实验结果表明,该模型的平均绝对误差(MAE)为6.714,均方根误差(RMSE)为60.961,预测误差均低于其他模型;且决定系数(R2)为99.472%,表明预测值和真实值较为接近。该模型对股票价格预测的效果较好。
关键词:股价预测;股票价格;残差神经网络;门控循环单元
中图分类号:TP183;F832.5 文献标识码:A 文章编号:2096-4706(2023)04-0113-04
Stock Price Prediction Based on Parallel ResNet-GRU Model
ZHAO Meng, WANG Qianying
(Hebei University of Economics and Business, Shijiazhuang, Hebei 050061, China)
Abstract: Aiming at the problem that the current stock price prediction model changes the gradient extremely as the number of layers of the network increases, a parallel ResNet and GRU network model are proposed to predict the closing price of stock data. Experimental results on the CSI 300 stock price data show that the Mean Absolute Error (MAE) of the model is 6.714, the Root Mean Square Error (RMSE) is 60.961, and the prediction error is lower than that of other models. And the coefficient of determination (R2) is 99.472%, which indicates that the predicted value and the true value are relatively close. The model has a better effect on stock price prediction.
Keywords: stock price prediction; stock price; ResNet; GRU
0 引 言
在股票时间序列数据中存在许多噪声信息和不确定性因素,是一个具有非线性、非平稳性和长期记忆性等特点的复杂系统,准确预测股票价格可以降低交易风险且对于投资者来说具有重要意义。
股价预测的传统方法有多元线性回归法、自回归移动平均法(ARIMA)等。如李俊豪[1]通过使用因子分析改进的多元线性回归模型对贵州茅台股票的收盘价进行预测;刘松等[2]通过建立ARIMA模型对西南证券股票的短期数据收盘价进行研究;齐天铧[3]建立了灰色模型和ARIMA模型,分析了模型的应用场景并对股票价格进行预测。近年来,伴随着人工智能网络技术的飞速发展,机器学习和深度学习等算法在各领域中得到广泛应用。通过引入支持向量机、神经网络等方法,进而由线性回归过渡到非线性模型的拟合,来对股价进行预测研究[4-9]。然而,伴随着预测周期的加长和网络层数的增加,容易产生梯度极端变化等问题[10],这样会使得模型的预测效果较差。残差神经网络可以简化深层网络的训练,避免模型梯度的极端变化问题。
综合以上模型思想,提出一种并联ResNet-GRU模型方法对股票价格进行预测。该模型通过引入残差卷积神经网络和记忆循环神经网络技术对股票价格数据进行训练以提取高维特征。利用了并联残差神经网络(Residual Neural Network, ResNet)的简化深层网络训练能力和门控循环单元(Gate Recurrent Unit, GRU)网络对时间序列数据的记忆能力,将ResNet网络和GRU网络的输出结果进行拼接作为总输出。这进一步提升了对股票价格的预测精度。
1 模型构建
1.1 卷积神经网络(CNN)
卷积神经网络是具有局部连接和权重共享等性质的深度神经网络,其通常是由Conv层、Pooling层和全连接层共同组成。一般来说,在卷积神经网络中可以有一个或多个Conv层、Pooling层和全连接层。网络的基本模型结构如图1所示。具体内容有:
(1)Conv层。其作用是利用特征提取器(卷積核)对局部区域的特征进行提取,特征提取器的选择可以相同,也可以不同。
(2)Pooling层。也称采样层。作用是对区域特征值进行特征选择,从而降低特征维数,避免过拟合。常用的池化方式有两种:一种是最大值池化(Max Pooling),最大值池化是选取某个区域所有数值中最大的一个作为该区域的代表值;另一种是平均值池化(Mean Pooling),通常是选取区域内所有数值的平均值作为该区域的代表值。
(3)全连接层。其作用是连接所有特征,将卷积、池化输出的二维特征数据处理成一维特征向量,用来综合所有信息。
1.2 残差网络模型(ResNet)
与CNN模型相比,ResNet模型在其中加入了Shortcut直连边分支结构(也称残差连接(Residual Connection)),使其与残差单元以直连边拼接的方式实现来提升网络信息的传播效率。残差网络中的基本模块结构如图2所示。模块中包含两种映射:一是恒等映射,即图2中右侧的x连线;二是残差映射F(x),最终输出目标函数H(x)=F(x)+x。
图2中,输入数据通过两个卷积层得到:
F=W2σ(W1x) (1)
其中Wi代表权重,σ代表非线性函数relu,然后与一个Shortcut连接,再经过非线性函数relu,最终获得输出目标函数为:
H=F(x,{Wi})+x (2)
当输入维度与输出维度不一致时,在Shortcut处对x做线性变换WS,最终输出目标函数为:
H=F(x,{Wi})+WSx (3)
1.3 門控循环单元模型(GRU)
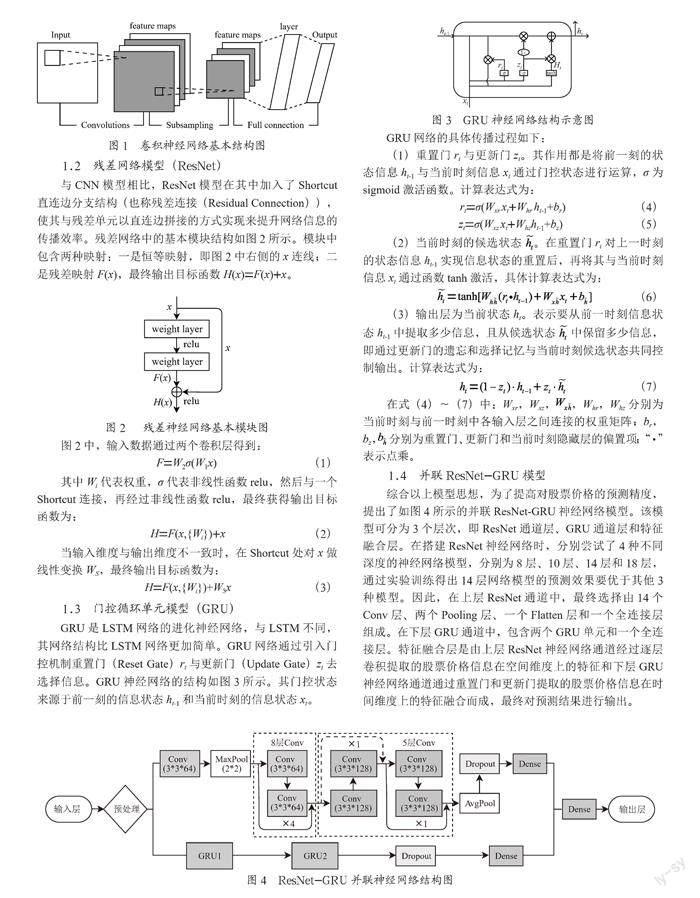
GRU是LSTM网络的进化神经网络,与LSTM不同,其网络结构比LSTM网络更加简单。GRU网络通过引入门控机制重置门(Reset Gate)rt与更新门(Update Gate)zt去选择信息。GRU神经网络的结构如图3所示。其门控状态来源于前一刻的信息状态ht-1和当前时刻的信息状态xt。
GRU网络的具体传播过程如下:
(1)重置门rt与更新门zt。其作用都是将前一刻的状态信息ht-1与当前时刻信息xt通过门控状态进行运算,σ为sigmoid激活函数。计算表达式为:
rt=σ(Wxr xt+Whr ht-1+br) (4)
zt=σ(Wxz xt+Whzht-1+bz) (5)
(2)当前时刻的候选状态 。在重置门rt对上一时刻的状态信息ht-1实现信息状态的重置后,再将其与当前时刻信息xt通过函数tanh激活,具体计算表达式为:
(6)
(3)输出层为当前状态ht。表示要从前一时刻信息状态ht-1中提取多少信息,且从候选状态 中保留多少信息,即通过更新门的遗忘和选择记忆与当前时刻候选状态共同控制输出。计算表达式为:
(7)
在式(4)~(7)中:Wxr,Wxz,,Whr,Whz分别为当前时刻与前一时刻中各输入层之间连接的权重矩阵;br,bz, 分别为重置门、更新门和当前时刻隐藏层的偏置项;“·”表示点乘。
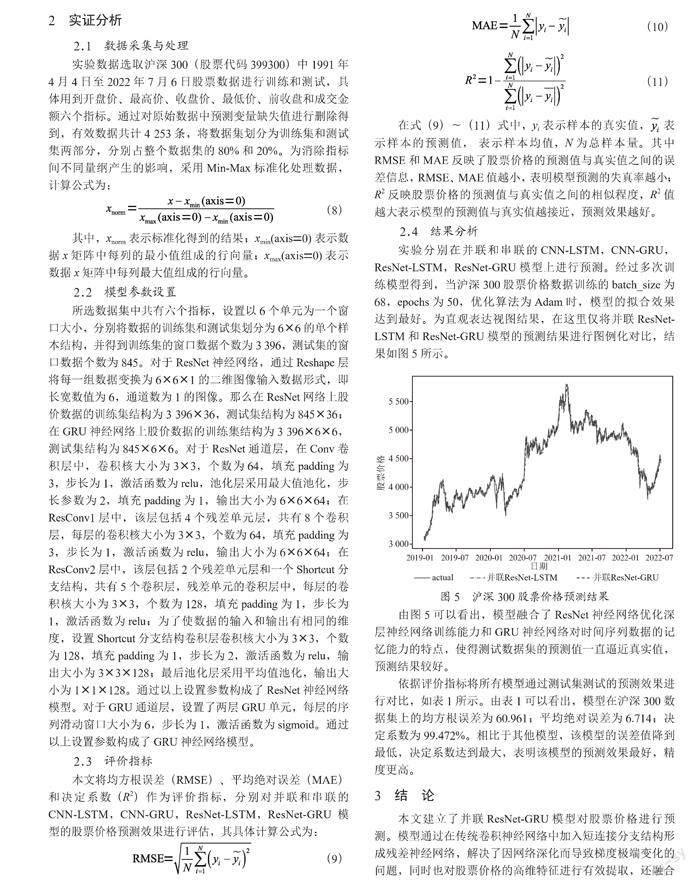
1.4 并联ResNet-GRU模型
综合以上模型思想,为了提高对股票价格的预测精度,提出了如图4所示的并联ResNet-GRU神经网络模型。该模型可分为3个层次,即ResNet通道层、GRU通道层和特征融合层。在搭建ResNet神经网络时,分别尝试了4种不同深度的神经网络模型,分别为8层、10层、14层和18层,通过实验训练得出14层网络模型的预测效果要优于其他3种模型。因此,在上层ResNet通道中,最终选择由14个Conv层、两个Pooling层、一个Flatten层和一个全连接层组成。在下层GRU通道中,包含两个GRU单元和一个全连接层。特征融合层是由上层ResNet神经网络通道经过逐层卷积提取的股票价格信息在空间维度上的特征和下层GRU神经网络通道通过重置门和更新门提取的股票价格信息在时间维度上的特征融合而成,最终对预测结果进行输出。
2 实证分析
2.1 数据采集与处理
实验数据选取沪深300(股票代码399300)中1991年4月4日至2022年7月6日股票数据进行训练和测试,具体用到开盘价、最高价、收盘价、最低价、前收盘和成交金额六个指标。通过对原始数据中预测变量缺失值进行删除得到,有效数据共计4 253条,将数据集划分为训练集和测试集两部分,分别占整个数据集的80%和20%。为消除指标间不同量纲产生的影响,采用Min-Max标准化处理数据,计算公式为:
(8)
其中,xnorm表示标准化得到的结果;xmin(axis=0)表示数据x矩阵中每列的最小值组成的行向量;xmax(axis=0)表示数据x矩阵中每列最大值组成的行向量。
2.2 模型参数设置
所选数据集中共有六个指标,设置以6个单元为一个窗口大小,分别将数据的训练集和测试集划分为6×6的单个样本结构,并得到训练集的窗口数据个数为3 396,测试集的窗口数据个数为845。对于ResNet神经网络,通过Reshape层将每一组数据变换为6×6×1的二维图像输入数据形式,即长宽数值为6,通道数为1的图像。那么在ResNet网络上股价数据的训练集结构为3 396×36,测试集结构为845×36;在GRU神经网络上股价数据的训练集结构为3 396×6×6,测试集结构为845×6×6。对于ResNet通道层,在Conv卷积层中,卷积核大小为3×3,个数为64,填充padding为3,步长为1,激活函数为relu,池化层采用最大值池化,步长参数为2,填充padding为1,输出大小为6×6×64;在ResConv1层中,该层包括4个残差单元层,共有8个卷积层,每层的卷积核大小为3×3,个数为64,填充padding为3,步长为1,激活函数为relu,输出大小为6×6×64;在ResConv2层中,该层包括2个残差单元层和一个Shortcut分支结构,共有5个卷积层,残差单元的卷积层中,每层的卷积核大小为3×3,个数为128,填充padding为1,步长为1,激活函数为relu;为了使数据的输入和输出有相同的维度,设置Shortcut分支结构卷积层卷积核大小为3×3,个数为128,填充padding为1,步长为2,激活函数为relu,输出大小为3×3×128;最后池化层采用平均值池化,输出大小为1×1×128。通过以上设置参数构成了ResNet神经网络模型。对于GRU通道层,设置了两层GRU单元,每层的序列滑动窗口大小为6,步长为1,激活函数为sigmoid。通过以上设置参数构成了GRU神经网络模型。
2.3 评价指标
本文将均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2)作为评价指标,分别对并联和串联的CNN-LSTM,CNN-GRU,ResNet-LSTM,ResNet-GRU模型的股票价格预测效果进行评估,其具体计算公式为:
(9)
(10)
(11)
在式(9)~(11)式中,yi表示样本的真实值, 表示样本的预测值, 表示样本均值,N为总样本量。其中RMSE和MAE反映了股票价格的预测值与真实值之间的误差信息,RMSE、MAE值越小,表明模型预测的失真率越小;R2反映股票价格的预测值与真实值之间的相似程度,R2值越大表示模型的预测值与真实值越接近,预测效果越好。
2.4 结果分析
实验分别在并联和串联的CNN-LSTM,CNN-GRU,ResNet-LSTM,ResNet-GRU模型上进行预测。经过多次训练模型得到,当沪深300股票价格数据训练的batch_size為68,epochs为50,优化算法为Adam时,模型的拟合效果达到最好。为直观表达视图结果,在这里仅将并联ResNet-LSTM和ResNet-GRU模型的预测结果进行图例化对比,结果如图5所示。
由图5可以看出,模型融合了ResNet神经网络优化深层神经网络训练能力和GRU神经网络对时间序列数据的记忆能力的特点,使得测试数据集的预测值一直逼近真实值,预测结果较好。
依据评价指标将所有模型通过测试集测试的预测效果进行对比,如表1所示。由表1可以看出,模型在沪深300数据集上的均方根误差为60.961;平均绝对误差为6.714;决定系数为99.472%。相比于其他模型,该模型的误差值降到最低,决定系数达到最大,表明该模型的预测效果最好,精度更高。
3 结 论
本文建立了并联ResNet-GRU模型对股票价格进行预测。模型通过在传统卷积神经网络中加入短连接分支结构形成残差神经网络,解决了因网络深化而导致梯度极端变化的问题,同时也对股票价格的高维特征进行有效提取,还融合了GRU神经网络对时序数据长期历史信息的记忆能力,并在沪深300的股票数据上进行实证分析。通过模型预测结果发现,与其他模型相比,该模型在评价指标上的效果较好,预测值与实际值的吻合度较高。这证实了残差神经网络的引入提高了模型对股价的预测性能。
参考文献:
[1] 李俊豪.基于改进多元线性回归的股票价格预测模型 [J].科技经济市场,2019(8):61-62+64.
[2] 刘松,张帅. 运用ARIMA模型对股价预测的实证研究 [J].经济研究导刊,2021(25):76-78.
[3] 齐天铧.基于灰色模型与ARIMA模型的股票价格预测 [J].计算机时代,2021(10):83-85+89.
[4] 徐浩然,许波,徐可文.机器学习在股票预测中的应用综述 [J].计算机工程与应用,2020,56(12):19-24.
[5] 张青.基于ARIMA-SVM组合模型的创业板股票价格预测分析 [J].广西质量监督导报,2019(12):131-132.
[6] 黄超斌,程希明.基于LSTM神经网络的股票价格预测研究 [J].北京信息科技大学学报:自然科学版,2021,36(1):79-83.
[7] 罗鑫,张金林.基于多时间尺度复合深度神经网络的股票价格预测 [J].武汉金融,2020(9):32-40.
[8] 张倩玉,严冬梅,韩佳彤.结合深度学习和分解算法的股票价格预测研究 [J].计算机工程与应用,2021,57(5):56-64.
[9] 赵红蕊,薛雷.基于LSTM-CNN-CBAM模型的股票预测研究 [J].计算机工程与应用,2021,57(3):203-207.
[10] HE K M,ZHANG X Y,REN S Q,et al. Deep Residual Learning for Image Recognition [C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition.Las Vegas:IEEE,2016:770-778.
作者简介:赵萌(1997—),男,汉族,河北邯郸人,硕士研究生在读,研究方向:调查与大数据分析;王倩影(1984—),女,汉族,河北保定人,副教授,博士研究生,研究方向:深度学习。
收稿日期:2022-08-03

