一种商空间理论下信息熵的属性权重确定方法

阎红灿,姚美红,郭小雨

(1. 华北理工大学 理学院,河北 唐山 063210;2. 河北省数据科学与应用重点实验室,河北 唐山 063210)

引言

现如今,评价某件事物的好坏已经不再通过单一的属性进行判断,事物的性质多由多个属性指标共同决定。因此,如何准确利用所给的多个属性数据,正确地对事物进行分类或排序问题不容小觑。属性权重体现了属性的重要程度,影响事物的排序结果,因而,准确客观地确定多属性权重的方法显得尤为重要。

自1965年查德提出模糊集合理论[1]的概念后,模糊综合评判法便越来越广泛地被应用到多属性权重确定。其中,模糊综合评判法的权重向量确定大多采用专家经验法或专家经验法与层次分析法[2](AHP)相结合的指标权重确定方法,这需要一定的背景知识,无法直接从所给数据得到想要的结果,因而在一些实际问题应用中存在一定的局限性。商空间[3]是粒计算三大主要模型与计算方法其中之一。商空间理论通过等价关系划分等价类,将等价类看成新元素,由这种新元素构成的空间就叫做商空间。不同的等价关系,可以划分不同的等价类,进而构成不同的商空间。在多属性权重的确定上,周丹晨把商空间理论与粗糙集理论结合应用于工作绩效综合评价[4]或系统日志挖掘[5]。前者不具有决策属性,通过样本之间的相似关系,利用模糊集的截集性质,建立分层递阶的商空间族,分析删除各属性后的等价类与商空间族的关系,以此得到属性的重要度。后者具有决策属性,但由于核属性集为空,无法用前者方式进行属性权重的计算与赋值,文章中采用条件熵的形式得到相对约简集,在相对约简集的基础上,进行识别规则的判断,得到不同样本的差异性。从后者可以看出,核属性集为空的状态下,无法进行多属性的权重赋值工作,只能通过置信度和覆盖度的差异得到不同样本之间的对比。

研究既无决策属性又无核属性时属性权重的计算问题。利用商空间理论下的分层递阶结构和信息熵的物理意义,在商空间基础上利用信息熵赋予属性以科学权重。提出的商空间理论上利用信息熵计算属性权重的方法,不需要背景知识,可以直接采用该方法对所给数据计算获得属性的客观权值,得到关于多目标方案的优劣排序。最后将此方法应用到油田开发的实例,将所得的油田开发排序结果与模糊综合评价法开发结果比较,验证该项研究所用方法的有效性和可靠性。

1相关理论

1.1 商空间

商空间理论用三元组(X,f,T)描述问题。X代表论域,f代表属性函数,T代表论域X的拓扑结构。按照等价关系对集合元素进行划分,把划分为同一类的元素整体看成一个新元素,由这种新元素构成的集合就是商集。通过划分,把原来的三元组(X,f,T)映射成(X1,f1,T1)。衡量构成的商空间是否符合需要解决的问题粒度时,可以借助效用函数(如近似精度与粒化程度)进行判断[6]。

不同的等价关系可以划分不同的商集。对于同一问题,可以在(X1,f1,T1)、...(Xn,fn,Tn)进行不同层次上的分析,最后对这些分析结果进行综合,得到关于问题的最佳解决方案。

定义1[7]:设R是X上的一个模糊等价关系,令Rλ={(x,y)|R(x,y)≥λ},0≤λ≤1}则Rλ是X上的一个普通等价关系,称Rλ为R的截关系。令等价关系Rλ对应的商空间为X(λ),可得到如下性质:若0≤λ2≤λ1≤1则Rλ1≥Rλ2,X(λ2)是X(λ1)的商集。于是,商空间族{X(λ)|0≤λ≤1}按照商集的包含关系构成一个有序链,称{X(λ)|0≤λ≤1}为X上的一个分层递阶结构。

1.2 信息熵

信息熵用来衡量不确定程度,即可以通过计算信息熵来判断一个事件的随机性及无序程度,也可以用来判断某个指标的离散程度[8]。熵通常被用来表述体系的混乱程度,熵越大,不确定程度越大,包含的信息量越小。

2商空间下信息熵的定义

商空间理论的思想就是从多个维度上对问题进行粒化分析,降低处理问题的复杂度。商空间理论不仅对论域进行分类,同时也对属性和结构进行分类,某种层面上体现了拓扑结构思想[10]。通过选取不同的阈值得到对应不同截集下的空间,这些空间构成了分层递阶结构的商空间。因此,在无决策属性的情况下,可以通过得到的商空间结果,作为决策分类结果。信息熵[11,12]是用来衡量系统混乱程度的指标,熵值越大分布越混乱,提供的信息量越小。因此,在对属性重要度进行分析与计算时,可以通过衡量属性的信息熵得出属性的权重。

属性权重的计算可以通过衡量删除属性前后等价类产生的变化[13],就是比较U/ind(C)与U/ind(C-ai)分类中样本所在等价类发生改变的个数。在无核属性的数据类型中,删除单个属性等价类不发生改变,考虑商空间理论下运用信息熵确定属性权重。

定义3:将阈值λ确定的商空间分类记为{X1,X2,...Xn},其中Xi代表等价类,数据的属性值类别记作sj。在阈值为λ的商空间中,属性的信息熵计算公式为:

(1)

|Xi|代表等价类中样本个数,|Xi(sj)|代表在Xi等价类下,属性的数据类别为sj的个数。通过计算Hλ,可以得到在阈值λ的空间下,属性所属类别在等价类中分布的混乱程度。Hλ越大,说明属性对该空间分类的贡献度越低,进而在该空间下的权重应越小。运用商空间下信息熵的方法计算属性权重,可以直接对等价类分析确定权重,保证方法的普适性。

3属性权重计算过程

3.1 数据的规范化处理

由于最初数据存在属性量纲不同的问题,导致属性数据之间处于不对等地位,因此在对属性重要度分析之前,首先要对数据进行规范化处理,使不同属性间的数据处于同一层面上时,才能对属性值进行操作,进而科学地得出各个属性的重要度。对于最初的数据,按属性是成本型或是效益型进行规范化处理,保证数据的整体统一性与处理便捷性。

属性值越小,对于综合评价时的样本起到正面影响的属性,称之为成本型属性,按公式(2)处理。

(2)

属性值越大,对于综合评价的样本起到正面影响的属性,称之为效益型属性,按公式(3)进行处理。

(3)

3.2 样本相似度计算

对于样本之间的相近程度,利用公式(4)余弦相似度计算每个样本之间的相似度rij(0≤rij≤1)。样本之间属性取值越接近,则样本间相似度越大。通过对样本相似度的计算,得到样本间的相似度矩阵R。

(4)

3.3 构造商空间

3.3.1构造分层递阶的商空间

对相似度矩阵进行传递闭包的计算,得到样本间的等价关系矩阵。利用样本之间的等价关系rij,取阈值λ,当rij≥λ时,将这2个样本划在一个等价类中,否则就在不同的等价类中,以此规则得到阈值为λ的商空间结构X(λ)。

取不同的λ,可以得到不同的分类,对应商空间中的不同层次,按阈值大小对层次排列,构成商空间的分层递阶结构。阈值越大,商空间中元素个数越多,λ=1时,每个样本单独一类。

3.3.2商空间多层结构下属性权重的计算

得到分层递阶结构后,利用定义的信息熵公式按3步计算属性权重。

(1)对规范化后的样本划分数据类别,即确定sj。通常按照[0,25),[25,50),[50,75),[75,100]分别对应1,2,3,4进行分类,例如xi=36则xi→2。对样本的属性空间做四分类处理,把商空间中的等价类元素由原始的x1,x2,x3,...形式,变成1,2,3,4,...形式。

(3)利用信息熵计算属性权重。属性在所有层次下的信息熵取平均值,作为属性的信息熵。信息熵越大,属性的重要度越小。对属性信息熵取倒数,作为属性重要度,为确保属性权重和为1,对属性重要度归一化处理,得到属性权重。

采用上述步骤处理可以做到直接对等价类分析确定属性的重要度,对比以往查看删除属性前后分类变化的方法,商空间下信息熵计算属性权重的方法对于无核属性的数据同样适用。

4应用算例与结果分析

为验证商空间理论下信息熵确定属性权重方法的可操作性和合理性,对某地区的8个油田,分别记为A、B、...、H,进行开发排序。油田的初始数据见表1所示。

表1 原始数据表

(1)其中:渗透率、孔隙度、含油饱和度、探明地质储量、含油面积、内部收益率属于效益型属性,采用(5)式进行计算处理。

(5)

剩余4个指标(原油黏度、产能建设投资、投资回收期、平均的单位成本)属于成本型属性,采用(6)式计算处理,得到表2。

(6)

采用上述方法处理原始数据,可以消除不同属性数据量纲的影响,为之后划分数据类别和确定等价类做基础。

将上述经过公式(5)与公式(6)计算后的数据,按照[0,25)、[25,50)、[50,75)、[75,100]分别对应1、2、3、4划分数据类别,得到表3。

表3 属性类别表

通过夹角余弦法如公式(7)计算,得到样本之间的模糊相似矩阵。

(7)

(8)

(2)利用模糊相似矩阵,建立传递闭包得到等价矩阵(9),建立分层递阶结构的商空间。

(9)

表4 样本商空间

通过计算删除各个属性后的等价类发现,分类结果不改变如式(10),因此无法使用删除属性后的分析等价类变化确定属性权重的方法。

(10)

在利用商空间理论得到分层递阶商空间结构的基础上,利用定义的信息熵公式计算属性ai在某个截集结构λ商空间下的信息熵Hλ。最后计算商空间族下的平均值,作为属性ai的信息熵H(ai),权重处理后归一化确定各属性的权重。

(11)

(12)

利用上述公式,举例属性a2在商空间λ5中的信息熵计算过程:

(1)通过表4查看商空间λ5样本聚类结果,通过表3查看属性a2的样本类别值。

商空间λ5的样本聚类结果:

λ5=X(0.803 4) {x2,x3,x4,x5,x8},{x1,x6},{x7}

样本的a2属性类别值:

x1=4,x2=4,x3=2,x4=2,x5=2,x6=2,x7=1,x8=1

(2)通过上步结果写出商空间等价类中属性的类别结果a2/λ5,利用商空间下信息熵公式计算。

商空间λ5下对属性a2的聚类结果为:a2/λ5={4,2,2,2,1},{4,2}{1}

故a2在λ5下的信息熵为:

以此方法所有属性在商空间下的信息熵,得到表5。

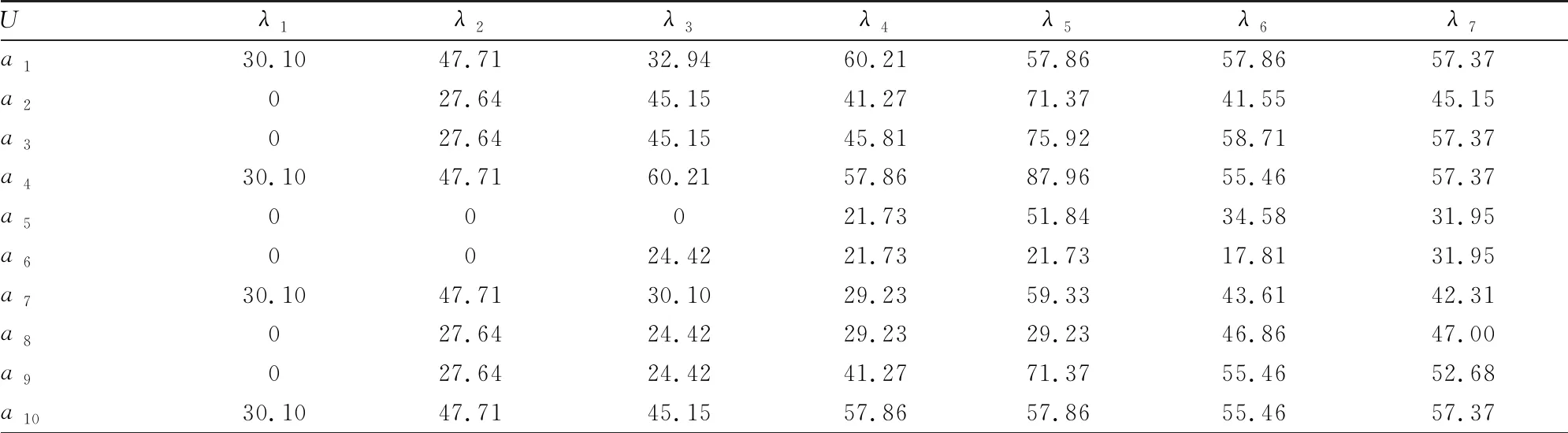
表5 属性在商空间下的信息熵/%

利用公式(11)取商空间信息熵总和的平均作为属性 在商空间下的信息熵,之后利用公式(12)进行权重处理以及归一化,得到属性的权重为:

利用属性权重对上述8个油田排序,排序结果与按照层次分析法和专家调查法综合[14]得到的排序结果相同。这进一步说明在商空间确定的分层递阶结构上通过定义信息熵计算属性权重的方法是合理科学的,并且该方法可以直接应用到客观数据上,不需要决策者有油田领域的背景知识,保证处理问题的方法具有便捷性和普适性。

5结论

提出了一种商空间理论上利用信息熵确定属性权重的方法,该方法成功地解决了多属性多目标排序问题中既无决策属性又无核属性的情况。通过将该方法应用于油田开发方案优选实例中,科学地对油田开发方案进行了排序。下一步将会在属性权重的基础上,研究属性约简。