防疫关键期公共交通供需冲突图模型研究

包渊秋，金 辉，吴特兰，杨晓光，3，徐 辉，李 晋

（1.悉地（苏州）勘察设计顾问有限公司，江苏 苏州 215123；2.苏州大学轨道交通学院，江苏 苏州 215131；3.同济大学交通运输工程学院，上海 200092）

在防疫关键期，即市域出现少量感染病例或疫情在一定范围内轻度蔓延时，具有鲜明社会公益性的大容量公共交通系统，以规范的运营和完备的防疫举措，在保障城市生活方面发挥着不可替代的作用[1]。特别为无替代出行方式的乘客，如低收入和无驾驶能力的群体，提供安全可靠的中长途出行服务。考虑到防疫关键期公交服务范围与服务策略的急剧变化，加之乘客出行行为的大幅调整，导致公交供需双方之间面临新的冲突。为此，亟须从服务供需匹配的角度，协调并确立公交供给方与需求方的策略，推进公交供需平衡，防止供需失衡导致的运营绩效、服务品质等问题，为后疫情下的交通系统有序恢复和可持续发展奠定基础。

从需求的角度看，乘客在防疫关键期会尽可能避免使用公交出行，即公交客流大幅降低[2]。新冠疫情对公交服务的冲击显著大于对私家车、自行车等出行模式的冲击，公交客流降幅达90%[3]。特别在乘客的消极心理作用下，亟须基于乘客出行需求灵活配置公交资源[4]。疫情严重程度越高，居民出行频次越低，公交分担率低至6.3%[5]。实际上，2020 年2 月新冠疫情之初，近50%的乘客停止使用轨道交通[6]。而随着疫情蔓延，90%的乘客停止轨道交通出行[7]。

从供给的角度分析，疫情防控期间，公交系统一般采用停运线路、取消站点及减少发车班次等策略，调控公交供给。新冠疫情暴发时，全国十余个城市的轨道交通线路全部或部分停运[8]；更有城市采取封城等措施，进一步减少了公交客流[9]。实际上，基于传播模型模拟病毒在公交系统内的传播过程，发现只需停运少量线路，即可在保障线路可达性的前提下，遏制疫情通过公交服务传播的风险[10]。亦可结合需求响应公交、预约乘车等精细化管理策略，提高公交服务的可用水平[11]，降低公交供给减少对乘客的负面效应[9]。预约进站及车厢拥挤监测等调节供给的措施，也可降低疫情交叉感染的风险[7]。在疫情社交距离的约束下，构筑兼顾公交运营、乘客出行及系统损失的混合整数规划模型，最优调配公交调度与发车间隔[12]，从而提高公交供给的可靠性和运营效率。

面对防疫关键期公交需求与供给的显著变化，亟须采取恰当的调控措施，协调公交供需关系，保障公交运营效率与服务吸引力。经典博弈论要求决策者须依据精确的偏好信息求解冲突均衡解。考虑不确定的外界因素及决策者态度，很难准确量化各方的偏好信息。冲突图模型则在相对偏好的基础上，对决策者的冲突行为建立数学模型，分析难以定量描述的冲突行为，解决多主体和多目标的博弈问题[13]。例如，面向公交设施建设与城市历史建筑保护的矛盾，构建冲突图模型，通过分析各方态度，确立优化公交路线达到协调多方意见的方法[14]。面向传统与网约交通服务的竞争问题，构建两阶段冲突图模型，为解决新旧交通商业模式的冲突提供理论与方法参考[15]。

采取冲突图模型，分析防疫关键期公交供需的博弈关系。基于供给方与需求方对不同策略的偏好水平，决定供需平衡状态，从而为应对防疫关键期公交供需的急剧变化和促进供需新平衡态的形成，提供理论与方法基础。

1 冲突图建模

1.1 冲突图理论与模型

冲突图模型是对冲突行为进行规范建模与分析的辅助决策方法，包括建模和分析两个步骤。建模即用图模型表示冲突，包括识别冲突、剔除不可行状态、绘制状态转移图等。分析则在稳定性定义下，获取冲突的均衡解[16-19]。

冲突图模型通常表示为[16-18]

式中：N 为冲突中所有决策者的非空有限集N={1，…，n}；S 是所有决策者策略组合的可行状态 （简称状态）S={s1，s2，…，sw}；D 为所有可行状态转移形成的集合；{≻i，∽i}i∈N是决策者偏好信息的集合，决定了对可行状态的偏好排序[20]。

对任意两个不同的可行状态sk和st，当决策者i 认为状态sk优于状态st时，记作sk≻ist；当决策者i 对状态sk和st的偏好相同时，记作sk～ist；当决策者i 对状态sk的偏好不低于状态st时，记作。可采用优序图法，简单、直接地明确冲突中决策者对策略的相对偏好。优序图法通过对策略进行两两对比，确定策略之间的相对偏好，具有操作简便、结果可靠的优点。

图1 是可行状态单边转移过程的示意图：当状态s0与另一状态有且仅有一个策略不同时，该状态仅需改变决策者i 的一个策略即可转移至另一状态，其形成的可达状态集合表示为Ri（s0）。其中，椭圆s0、s1和s2表示可行状态，有向弧表示冲突中多方决策者控制的状态转移，弧的箭尾和箭头分别表示初始状态和转移后的状态，双向弧则代表转移可逆。若s0可通过一次单边转移，实现状态优化，则称之为状态的单边改进，其形成的单边改进集可表示为（s0）[17]。相应地，除决策者i 外的其他决策者（N－i）在状态s0实现的状态单边转移和改进集合，分别表示为RN－i（s0）和。

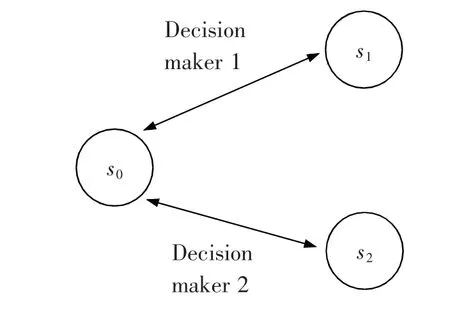
图1 可行状态单边转移图Fig.1 Diagram of unilateral of feasible states

1.2 冲突稳定性

若决策者不愿从当前状态转移到其他任意状态，说明该状态具有稳定性。结合决策者的预见力和风险态度，可构建4 种基本稳定性，分别是纳什稳定、一般超理性稳定、序列稳定和对称超理性稳定[18-19]。

从表8可知：处理1相对于处理2、处理3对苹果产量的影响显著；处理2相对于处理3对苹果产量的影响不显著。

1）纳什稳定是一步稳定，决策者理性地选择对自身最有利的状态，不考虑其他决策者的行为。若决策者无法通过改变策略而使自身转移到更优状态，则达到稳态。即（s0）=Ø。当冲突中所有决策者都达到纳什稳定时，为强稳态[17]。

2）一般超理性稳定为两步保守稳定，决策者考虑其他决策者所有可能的制裁，若当前状态s0无法改进，则达到稳态。即使s0≳is2。

3）序列稳定是两步冒险型策略，认为对手在反击时仅考虑对自己更优的状态，若当前状态s0无法改进，则达到稳态。即使得s0≳is2。

4）对称超理性稳定为三步稳定，在一般超理性稳定的基础上，决策者进一步考虑逃脱其他决策者的制裁，当回应后的状态不优于初始状态s0，则达到稳态。即∀s1∈，∃s2∈RN－i（s1），使得s0≳is2；且对∀s3∈Ri（s2），有s0≳is3。

对某种稳定性而言，若某状态使得所有决策者（∀i∈N）达到稳态，则为冲突稳态。图2 分析了4 种稳定性类型的相对关系。其中，一般超理性稳定包括了纳什稳定、序列稳定与对称超理性稳定；满足纳什稳定的可行状态一定同时满足其他稳态[16-17]。纳什稳定下的稳态是强稳态，是冲突的理想均衡解。

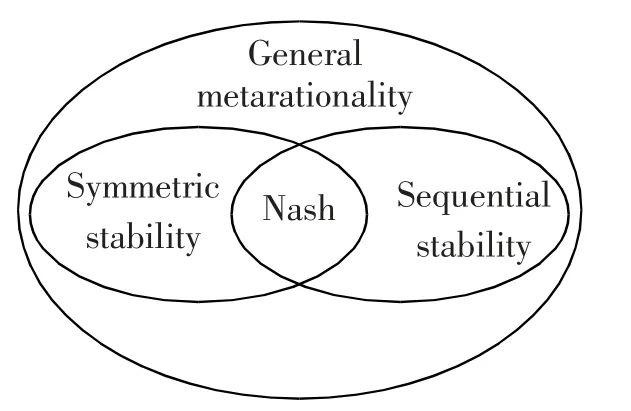
图2 4 种稳定性类型的相对关系Fig.2 Relations of 4 types of stability definition

2 公交供需策略与冲突关系

2.1 公交供需策略

防疫关键期公交供需策略急剧变化，其内在博弈关系也随之演化。为预防交叉感染并降低运营成本，公交供给方一般采用停运隔离区线路、减少发车班次等方式，导致乘客出行时间增加等负效益。相应地，为规避感染风险，出行者减少使用公交[4]，导致部分线路和站点的公交客流骤降，造成运力浪费。

图3 总结了防疫关键期公交供需双方的基本策略。其中，A1，A2 是公交供给方对全部线路进行统一调整，分别采取停运所有公交线路，将所有线路班次减少50%的措施；A3 则为针对性的局部调整，仅停运隔离区的公交线路。B1 表示公交需求的保守型出行策略，即完全不使用公交出行；B2，B3则为针对疫情态势制定的灵活出行策略，分别为停止使用隔离区的公交，在非必要的情况下不使用公交。其中，A1 和B1 可直接切断疫情传播途径，而其他策略则存在轻微的疫情感染风险，须通过行为引导（如佩戴口罩、减少接触）强化出行安全。

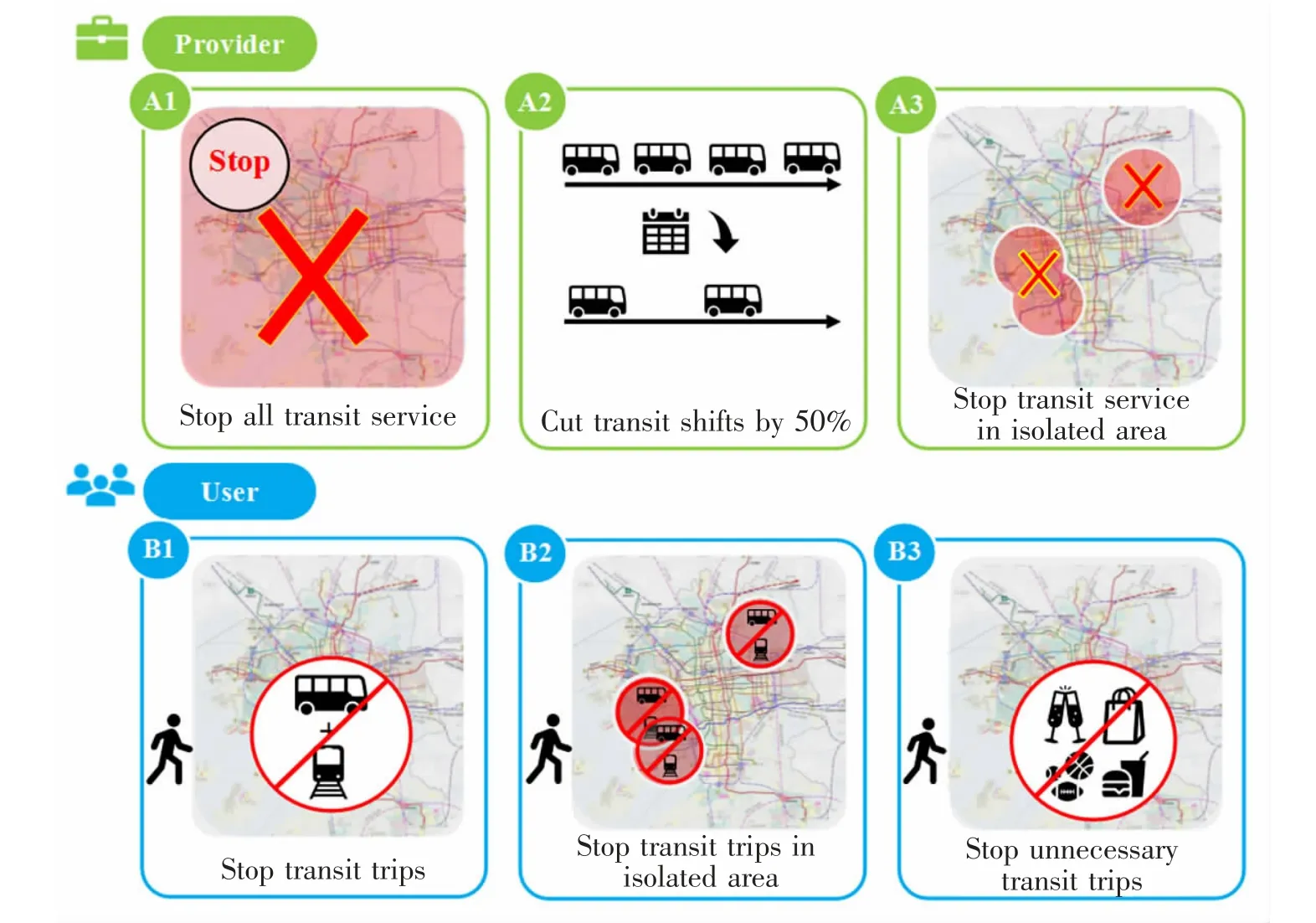
图3 防疫关键期公交供需双方的策略Fig.3 Strategies of transit provider and user in the critical period of epidemic prevention

2.2 可行状态与单边转移

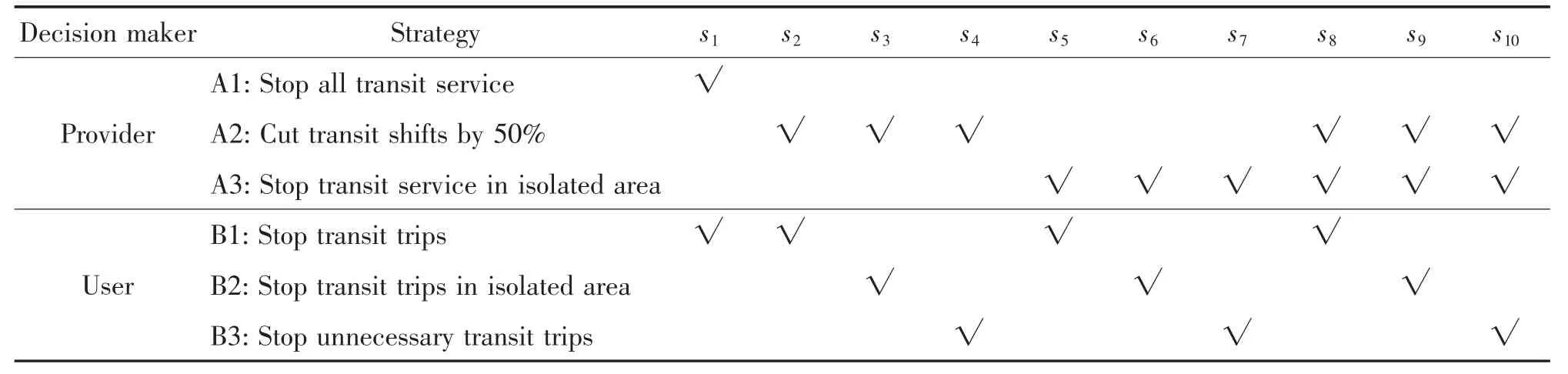
表1 防疫关键期公交供需冲突可行状态列表Tab.1 Feasible conflict states between transit provider and user in the critical period of epidemic prevention

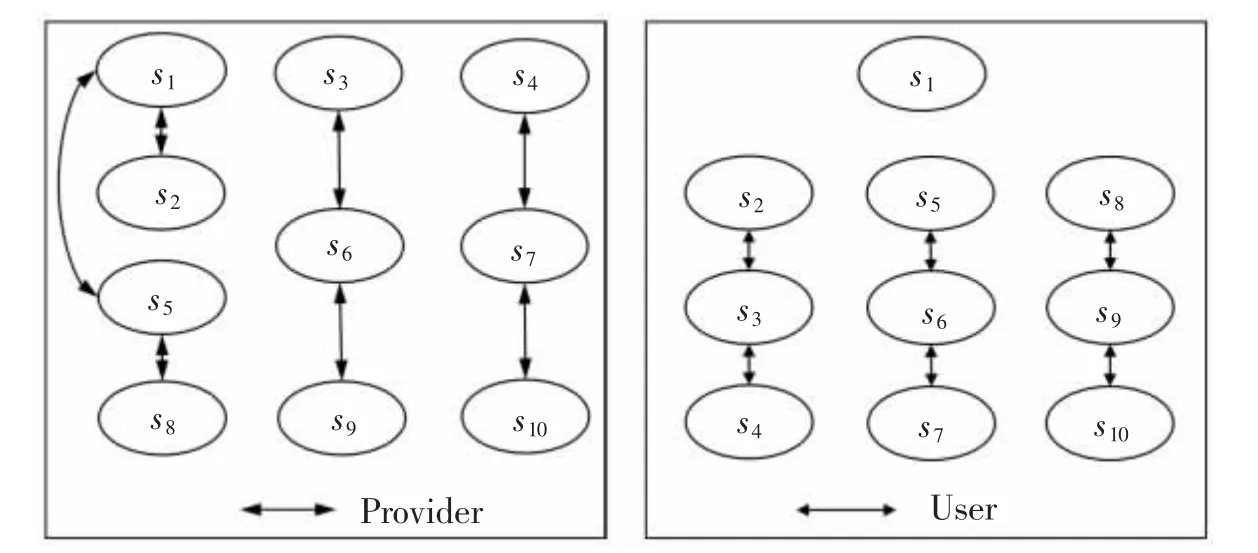
图4 防疫关键期公交供需双方的可行状态单边转移关系Fig.4 Unilateral transfer of feasible states of transit provider and user in the critical period of epidemic prevention

3 实例研究

3.1 数据调查

面向苏州公交公司管理人员与公交乘客，采取线上线下结合的问卷调查方式，采集公交供给方（公交公司管理人员）与需求方（乘客）对前述6 个策略的偏好信息。其中，1 分表示决策者“完全不赞同”，10 分表示决策者“完全赞同”。

调查获得公交供给方和需求方各36 份和688份有效问卷。为确保问卷数据的可靠性，采用克朗巴赫α 系数进行信度检验，当α≥0.7 时，数据内在一致性较好。利用SPSS 软件，分析公交供需双方对各策略的偏好数据，发现其α 系数分别为0.76 和0.87，符合上述检验要求。进一步计算供需双方各策略的平均偏好，见表2。

表2 防疫关键期公交供需双方策略的平均偏好Tab.2 Average strategy preference of transit provider and user in the critical period of epidemic prevention

3.2 相对偏好

针对前述的6 个供需策略及其偏好，建立6×6的优序图，比较左侧竖列与顶部横行策略的偏好，获得策略之间的相对偏好，如表3。其中，“1”表示竖列的策略偏好大于横行的策略，而“0”表示竖列的策略偏好较小，若两者相等则为0.5。例如，对供给方而言，策略A1 和A2 的平均偏好分别为3.8 和7.4，故行A1 和列A2 对应的相对偏好为1，而列A1和行A2 对应的相对偏好为0。

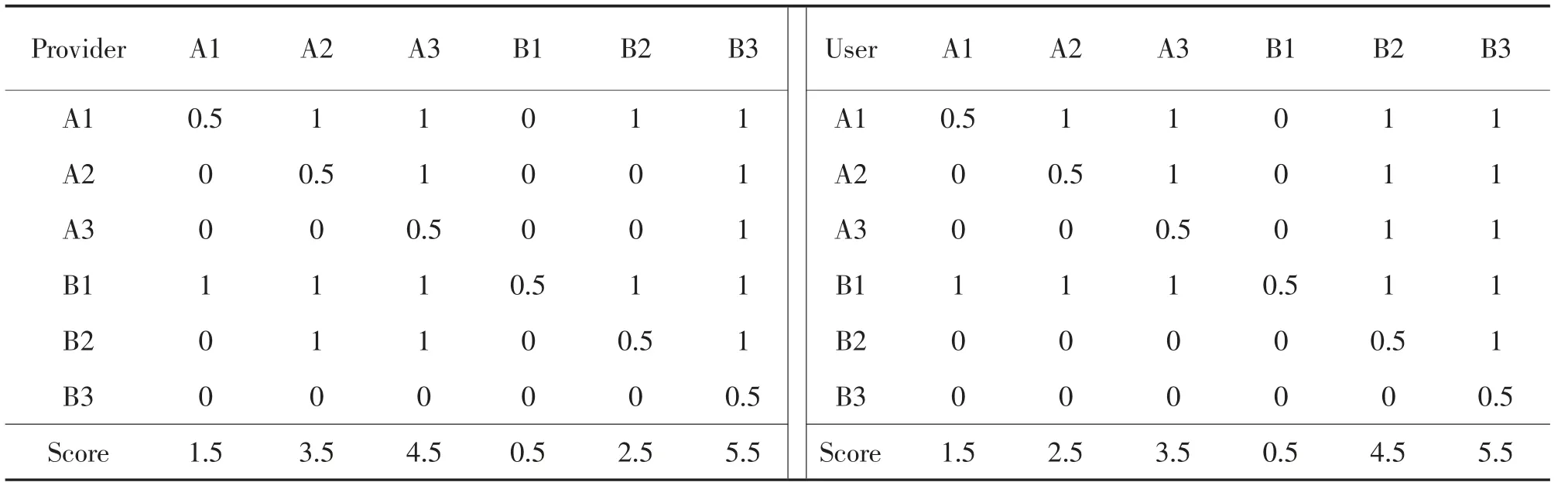
表3 防疫关键期公交供需双方策略的相对偏好Tab.3 Relative strategy preference of transit provider and user in the critical period of epidemic prevention

分别对供需双方每个策略偏好的得分进行竖向累加，得到单个策略的相对偏好。将其与供需各方所有策略偏好得分之和相除，作为该策略对各方的偏好占比，如表4 所示。将各个可行状态对应的供需方策略偏好加和，得到各状态的偏好，由此得到公交供给方与需求方对可行状态的偏好结果。各可行状态偏好的排序如表5 所示。

表4 防疫关键期公交供需双方策略的偏好占比Tab.4 Proportion of strategy preference of transit provider and user in the critical period of epidemic prevention%

表5 防疫关键期公交供需双方的可行状态偏好Tab.5 Feasible state preference of transit provider and user in the critical period of epidemic prevention

由此可得到各状态的单边改进情况，如图5 所示。其中，状态s1是公交停运且乘客停止公交出行，其对应的偏好最低。在此状态下，公交供给者停止所有服务，而需求方则被迫转向其他出行方式，导致公交服务功能完全丧失。状态s10是供给方减少所有线路一半班次并停运隔离区公交、需求方停止非必要公交出行，其对应的偏好最高。该状态的偏好显著高于其他状态，说明结果具有较好的可靠性。状态s10可有效减少防疫关键期公交出行过程的社会接触，同时保障出行者对公交服务的基本需求，可有效促进供需新平衡。表6 总结了公交供需双方的单边转移集Ri（s）和单边改进集。

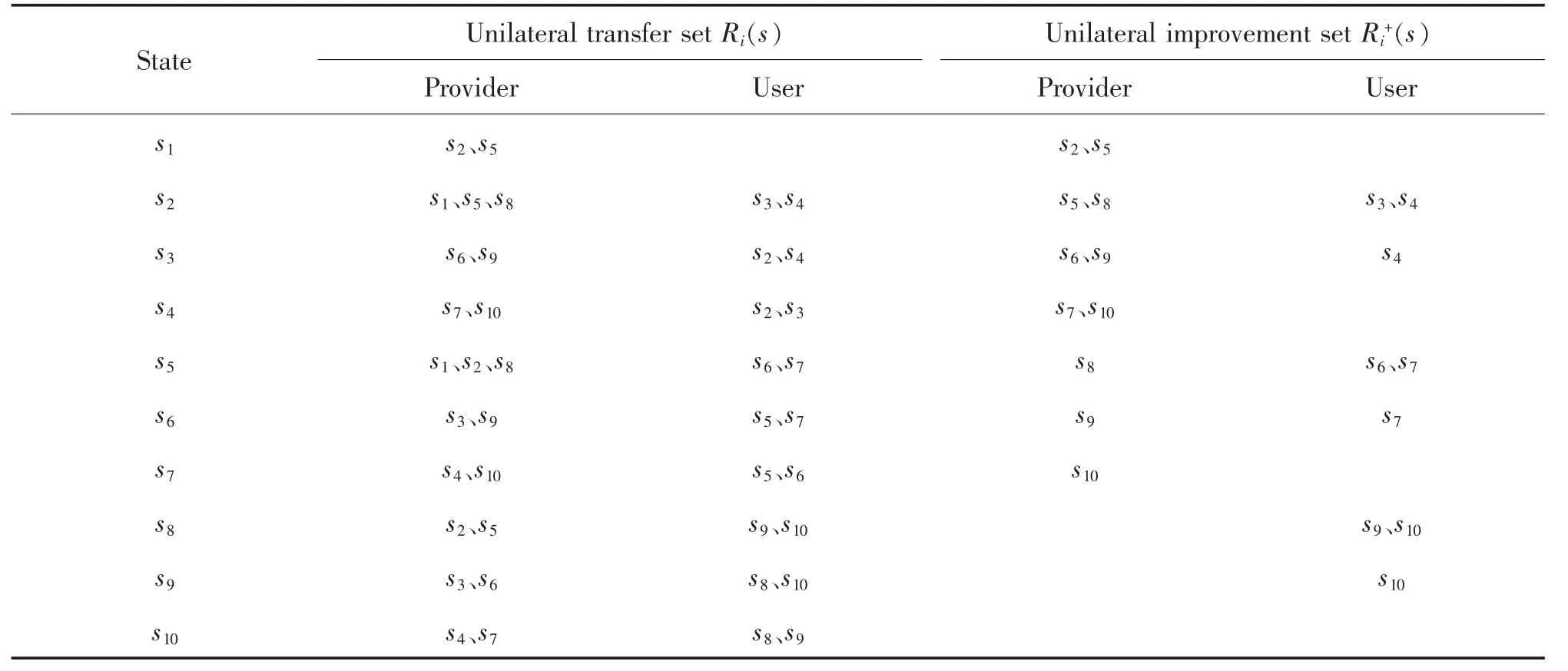
表6 供需双方的单边转移与改进集Tab.6 Unilateral transfer and improvement sets of feasible states of transit provider and user

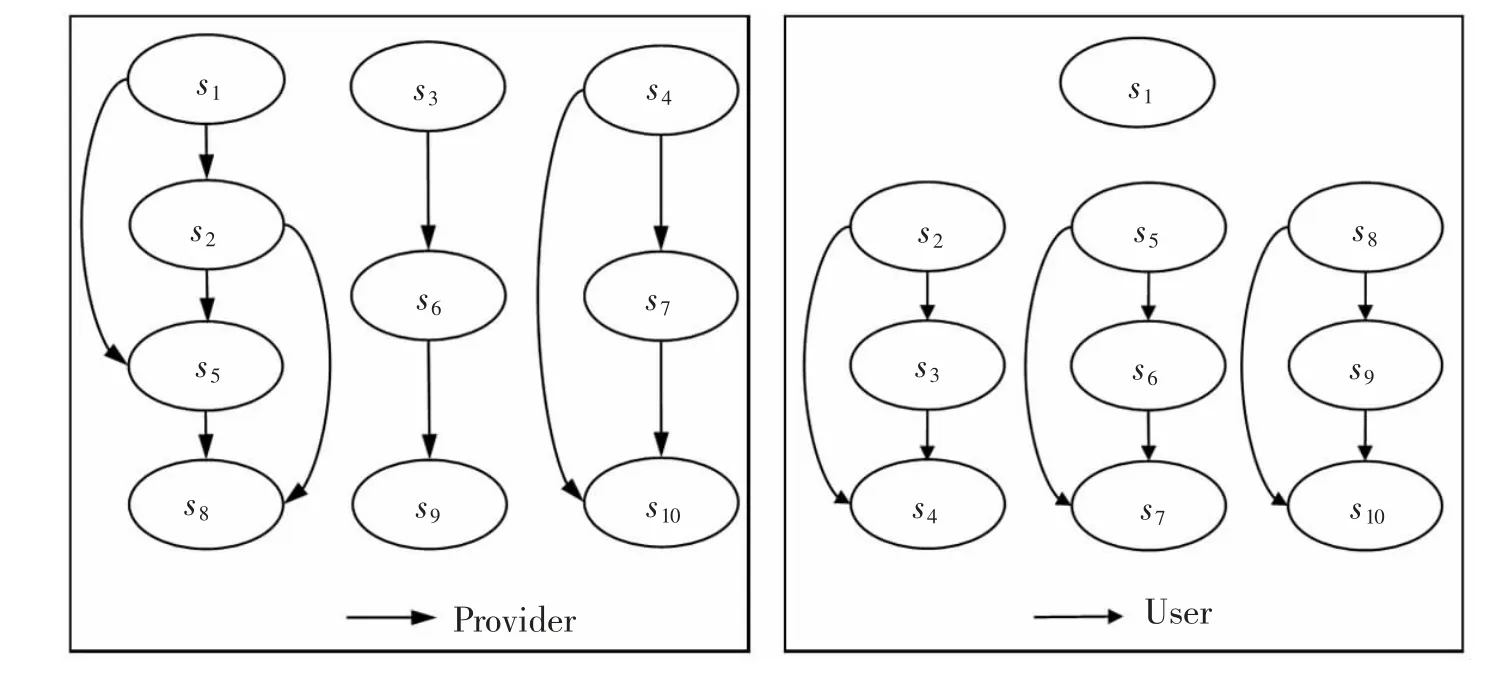
图5 防疫关键期公交供需双方可行状态的单边改进Fig.5 Unilateral state improvement of feasible states of transit provider and user in the critical period of epidemic prevention

3.3 偏好与稳态

结合前述4 种稳定性的计算方法，展开稳定性分析，如表7 所示。符号和分别表示，在某稳定性下，该状态仅对供给方或需求方稳定；符号●则表示该状态对供需双方均稳定，即稳态；符号★则表示纳什稳态，即冲突的强稳态；符号×表示未达到平衡。

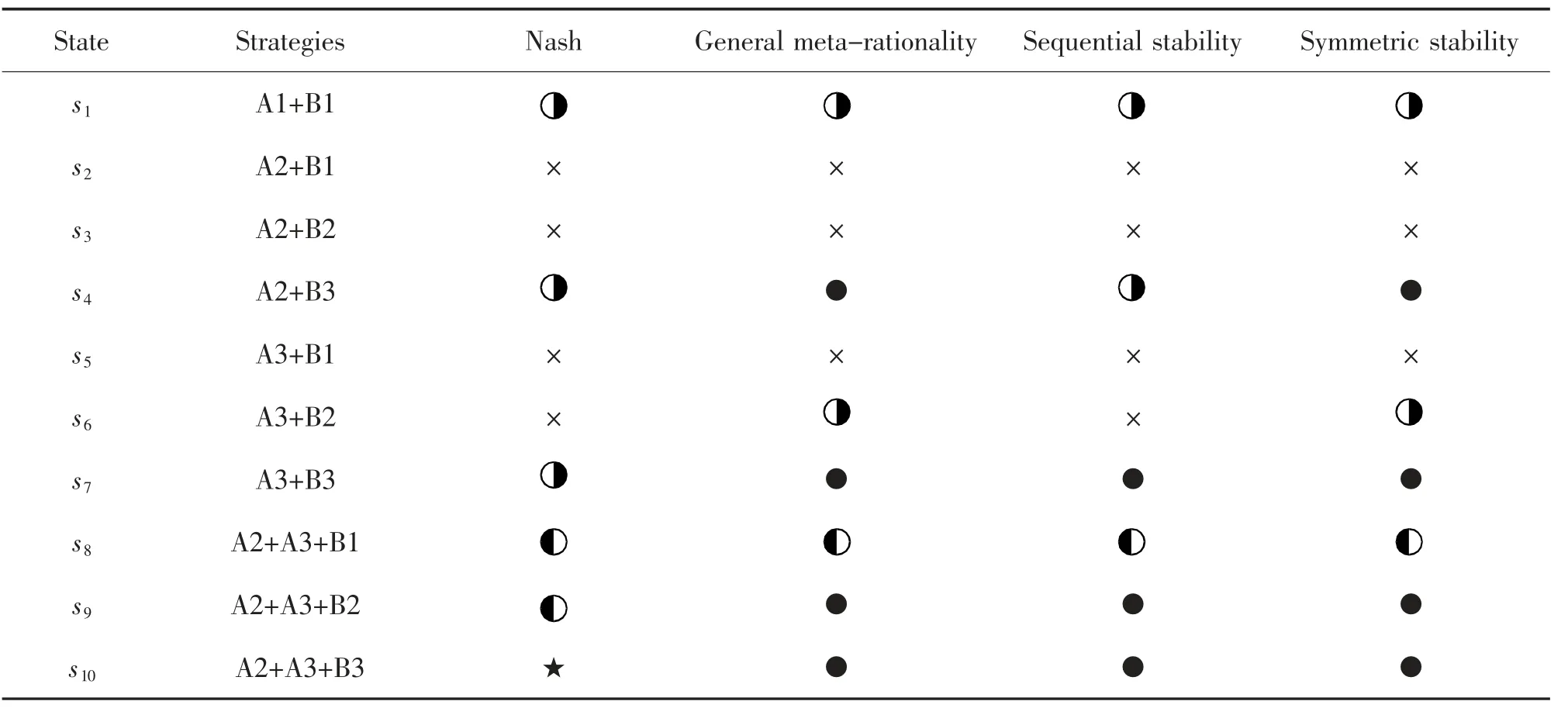
表7 防疫关键期公交供需冲突稳定性分析Tab.7 Conflict stability between transit provider and user in the critical period of epidemic prevention

图6 分析了防疫关键期公交供需冲突的稳态。其中，状态s4是一般超理性和对称超理性的稳态，通过削减一半班次和停止非必要公交出行，可有效避免防疫关键期公交运力的浪费和公交乘客的感染风险。状态s7、s9是一般超理性、对称超理性和序列稳定下的稳态。状态s7是s4状态将供给方策略由班次减半改为停运隔离区公交服务的单边改进，而状态s9则在状态s7的基础上增加了供给方同时采取班次减半的策略，可降低公交运力的浪费。将状态s9对应的需求方策略由停用隔离区公交改为非必要不使用公交，则可单边改进至状态s10，实现纳什稳定。该状态即为冲突模型的纳什均衡解，即公交供需冲突的强稳态。

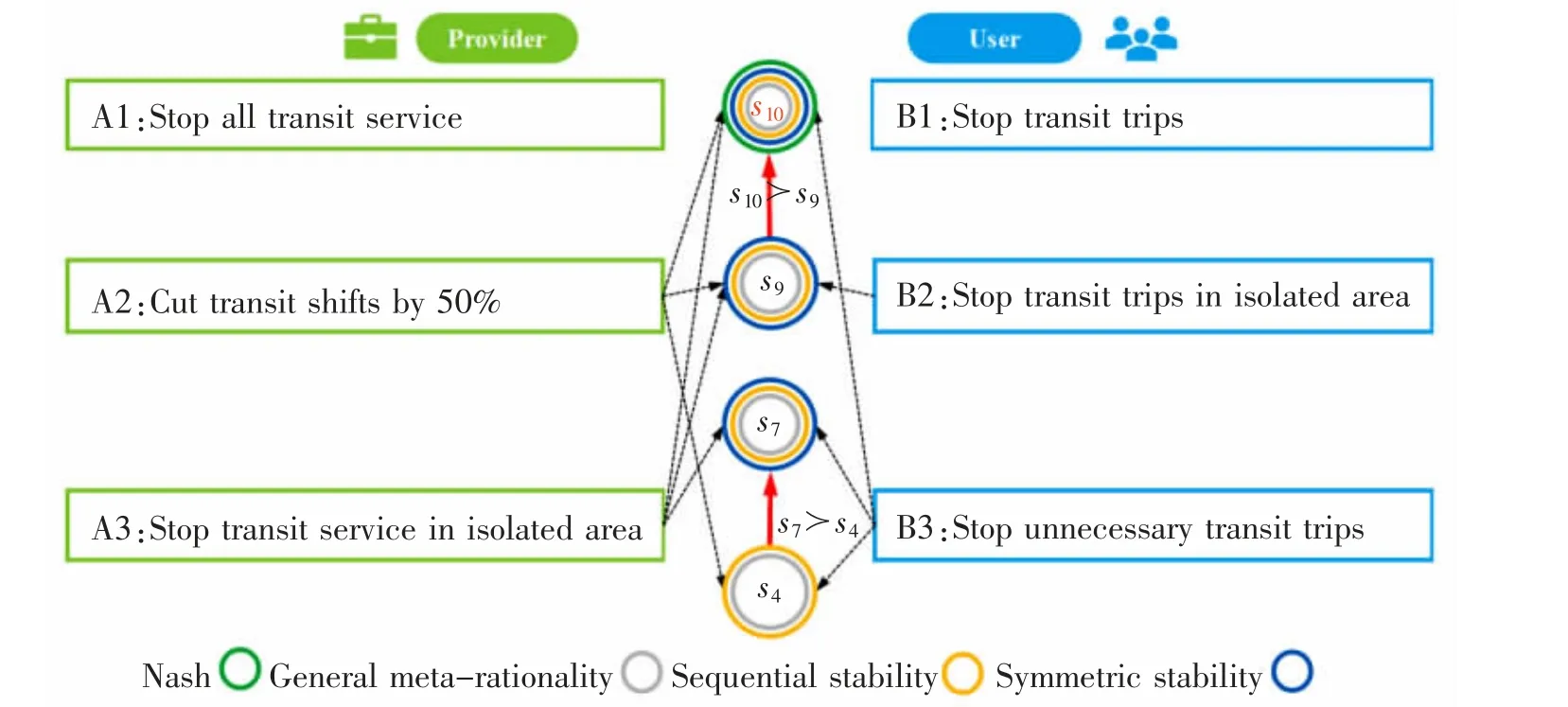
图6 防疫关键期公交供需冲突图模型稳态分析Fig.6 Analysis of stable states of conflict between public transit provider and user in the critical period of epidemic prevention

图7 示意了公交供需冲突的强稳态。该状态是防疫关键期公交供需双方偏好水平最高的策略组合，可同时减少公交服务的供给（即班次减半）与需求（即非必要不使用）。一方面减少公交供给的浪费、降低公交出行感染疫情的风险，另一方面在保障乘客出行的前提下，对乘客的出行行为起到引导与约束作用，促进供需双方在防疫关键期实现新的供需平衡。因此，该策略可充分适应防疫情况降低财政支出、减少公交服务浪费，和减少社会接触、非必要不出门的应对策略，具有较好的可靠性。为实现该稳态，应在需求为本的原则下，通过政策引导等方式，首先推动乘客出行需求的调整，即减少非必要的公交出行。待公交出行需求趋于稳定后，结合疫情分布，确定针对性的公交供给优化方案，调整公交的发车班次与服务范围。

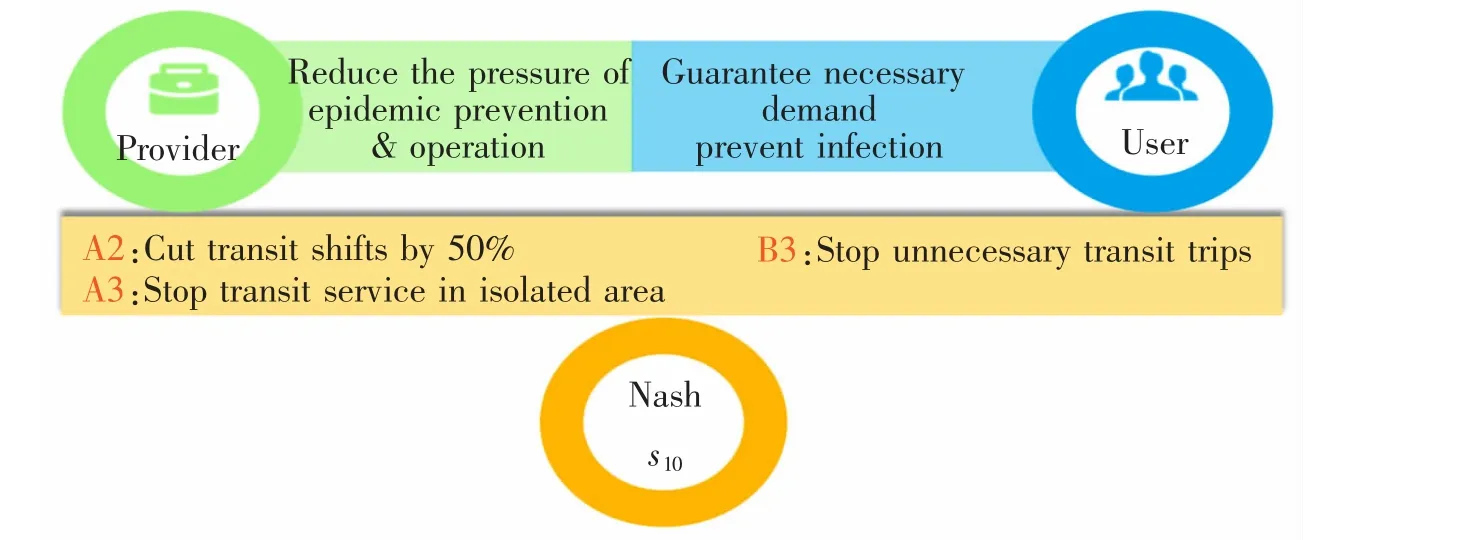
图7 防疫关键期公交供需冲突图模型纳什均衡解Fig.7 Nash equilibrium solution of conflict graph model between transit provider and user in the critical period of epidemic prevention

4 结论

1）防疫关键期公交供需状态的显著变化，导致供需之间存在冲突，亟须实现供需新平衡，而冲突图模型可清晰描绘双方的动态博弈关系。

2）当公交供给方采取班次减半和隔离区停运策略、需求方采取停用隔离区公交策略时，可达到除纳什稳定以外的三种稳定；将需求方策略进一步转为“非必要不使用公交”时，可实现冲突的纳什稳态，得到冲突的理想均衡解。

3）防疫关键期供需双方达到的强稳态可有效防控公交出行中感染疫情的风险，减少供给浪费，促进供需双方在防疫关键期实现新的供需平衡。