盾构开挖引起邻近单桩水平向变形解析研究

范秀江，冯国辉，薛芬芬，陈国平，窦炳珺，丁士龙，徐长节,4,5

（1.浙江省建投交通基础建设集团有限公司，浙江 杭州 310012；2.浙江大学滨海和城市岩土工程研究中心，浙江 杭州 310058；3.中国地质大学（武汉）海洋学院，湖北 武汉 430074；4.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013; 5.华东交通大学江西省岩土工程基础设施安全与控制重点实验室，江西 南昌 330013）

相比于前人研究的室内试验[1-2]和有限元模拟[3-4]，理论解析的方法常用来初步估算盾构开挖引起既有桩基水平向应力应变解答。大多基于两阶段分析法：第一阶段分析隧道开挖引起周边土体自由位移[5]；第二阶段通过建立桩基单元体受力平衡方程求解得到既有桩基变形响应[6-7]。梁发云等[8]基于Winkler 地基模型和最小势能原理解析获得邻近桩基在隧道开挖下的变形响应；可文海等[9]基于Winkler 地基和函数叠加法获得群桩竖向沉降解答。相比于Winkler 地基模型，Pasternak[10]地基模型能够考虑土体剪切效应，更能准确预测土与结构相互作用过程。冯国辉等[11]基于单参数Winkler 和双参数Pasternak 地基研究了隔离桩可减小盾构掘进引起既有高铁桩基水平位移；Zhang 等[12]基于Pasternak地基模型及桩侧土体影响展开了桩-土相互作用研究，并获得了两种不同情况下隧-土-桩相互作用差分解；梁发云等[13]基于欧拉梁和双参数地基得到既有桩基在邻近开挖下的应力应变响应；程康等[14]基于铁木辛科梁和Pasternak 地基模型获得了既有桩基在邻近隧道开挖下的简化计算方法。为了更加准确反映土与结构的相互作用，Zhang 等[15]和冯国辉等[16]基于Kerr 地基模型[17]获得地下空间开挖引起邻近地下构筑物变形解析。

综上所述，隧道开挖引起邻近桩基受力变形的理论解析大部分基于Winkler 和Pasternak 地基模型，较少学者采用Kerr 地基模型来模拟桩-土相互作用。本文在前人研究的基础上，采用两阶段法获得桩基水平向解析解。和既有有限元数据比对，证实了该方法的正确性。

1 解析过程

1.1 土体自由位移求解

由Loganathan 等[5]可知土体自由位移场Sx会随邻近隧道开挖的影响为

式中：ε0为地层损失比；R 为隧道半径；x 为桩-隧水平方向距离；H 为隧道埋深；z 为任意点埋深；v 为土体泊松比。

1.2 桩基水平位移解析过程

隧道开挖后，引起既有桩基的附加应力为q。此时，基于Kerr 地基的桩-土相互作用见图1。

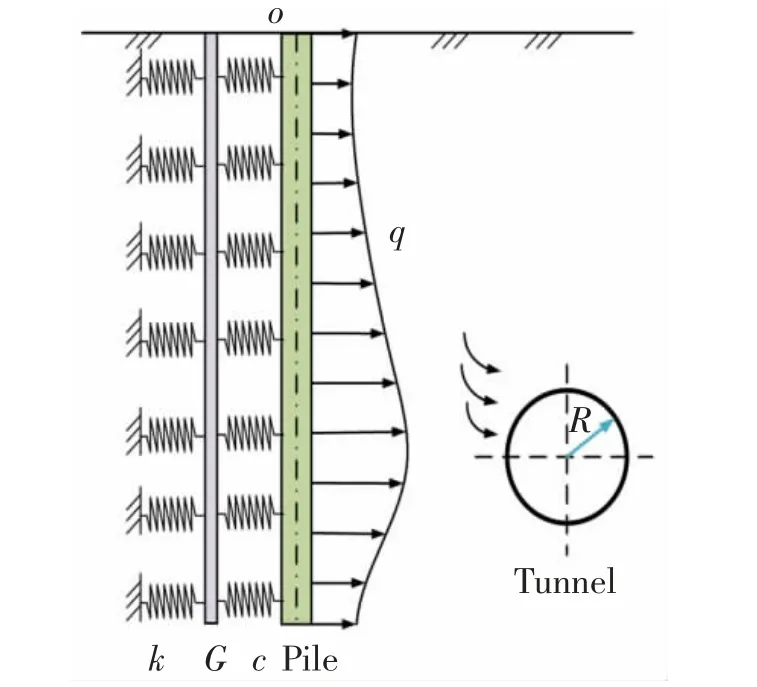
图1 Kerr 地基模型示意图Fig.1 The Kerr foundation model

1.3 计算过程

由Kerr 地基模型特性可知

式中：w1为下层弹簧的变形；w2为上层的变形。下层弹簧及剪切层下方的应力q1与q2分别为

式中：c，k 分别为上层，下层弹簧刚度。

由剪切层特性可知

结合式（3），式（5），可得

式中：G 为剪切层刚度。

桩基单元体受力平衡如图2 所示。

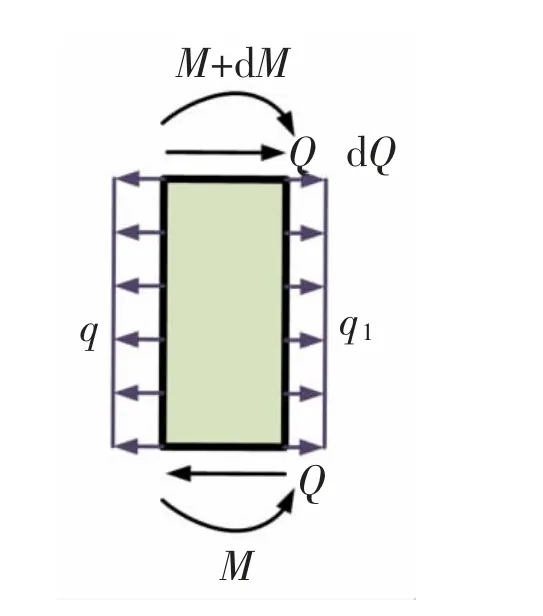
图2 桩身微单元受力示意图Fig.2 The force of pile element

力的平衡为

弯矩平衡为

式中：Q 和M 分别桩基剪力和弯矩；dx 为桩基微单元增量；dQ 和dM 分别为桩基沿纵向方向剪力及弯矩的增量。

结合式（7），式（8），可得

由材料力学可知

由桩体水平向受力平衡可知

式中：EI为桩基抗弯刚度。

结合式（5），式（6）及式（11）可得

式中：q 为桩基受到的水平外荷载，可表示为

1.4 地基参数选取

根据Tanahashi[18]和Vesic[19]提出的经验公式，弹簧刚度k 以及土体剪切刚度G 可取为

式中：Es为地基模量；υ 为土体泊松比；t 为土体剪切层厚度；I 为桩基截面模量；D 为桩基直径。

参照简化弹性空间法[20]，Kerr 的地基参数c 取3 倍地基反力模量。

1.5 桩基水平受力平衡方程求解

式（12）为6 阶微分方程，由于其较难获得解析解，本文采用差分解获得其数值解。将既有桩基离散为n+7 个点（其中两端存在6 个虚点），相邻虚点之间间距为l，且l=L/n，其中L 为既有桩基埋深。桩基离散化为图3。

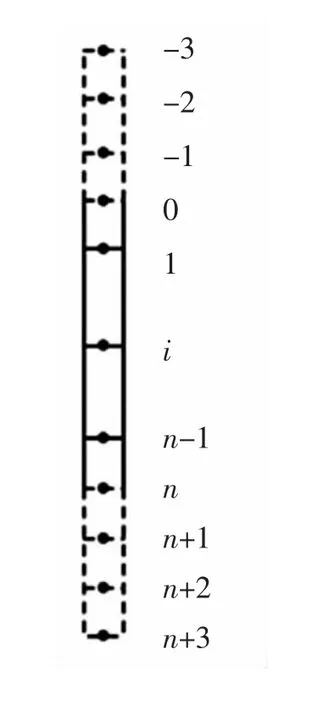
图3 桩基离散化Fig.3 The pile discretization

此时，式（12）可以简化成

此时，式（15）可以简化成：

式中：t（n）代表w2的n 阶导数；χ1，χ2，χ3，χ4分别为

根据实际两端边界条件进行简化，可将既有桩基两端简化成两个自由端[11,14,16]，这样便可消去桩基两端6 个虚拟单元，其矩阵形式为

式中t，F 表示如下

K 可表示为

此时，得到为w2（x）位移的解析解，通过式（6）即可得到桩基水平位移w（x）。同时，桩基弯矩和剪力也可通过欧拉梁特性得知。

值得注意的是，当Kerr 地基模型中参数c=0时，桩-土之间相互作用将退化成Pasternak 地基模型（E-P 模型）；当参数c=0 和剪切效应G=0 时，本文方法将退化成Winkler 地基模型 （E-W 模型）解析解。

2 算例验证

文献[21]曾采用应用有限边界元的程序GEPAN分析了多种不同的地层损失率情况下隧道开挖引起邻近桩基的变形响应，且该数据成功用于辅证既有论文解析的合理性[8]。其工况为：假设土体为均质弹性土，土体模量为24 MPa；单桩桩径为0.5 m，桩底埋深为25 m，桩基模量为30 GPa；隧道轴线埋深为25 m，隧道开挖半径为3 m，隧道轴线与桩基轴线水平净距为4.5 m，隧道与桩基相对位置如图4所示。为了验证本文方法的合理性，取其地层损失率1%的计算结果与本文计算结果进行对比。

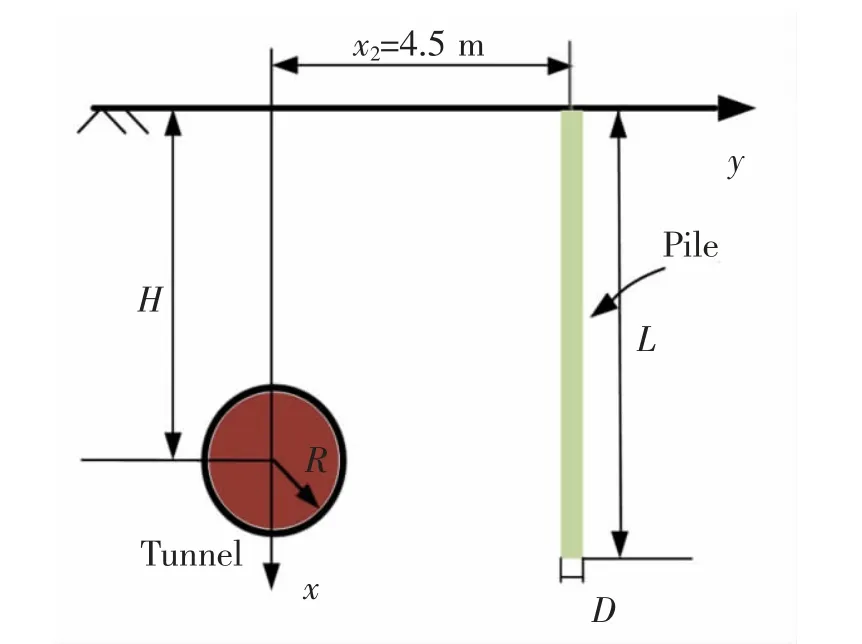
图4 隧道与桩基位置示意图Fig.4 Location diagram between tunnel and pile

本文方法位移和弯矩计算结果与GEPAN 数据对比曲线分别见图5 和图6，其GEPAN 数据来自文献[21]。由图5 和图6 可见，本文方法和本文方法退化解（E-P 模型和E-W 模型）与GEPAN 数据结果趋势一致，在隧道开挖的影响下，既有桩基会向隧道开挖的方向侧移，并且桩基最大侧移和弯矩值发生位移接近隧道开挖轴线埋置深度。采用本文方法计算得到桩基最大水平位移为9.1 mm，桩身最大弯矩值为56.9 kN·m；本文退化E-P 模型（即将既有隧道简化成Euler-Bemoulli 梁搁置在Pastemak地基模型上）计算结果稍微较小；其预测结果最大侧向位移为7.3 mm，弯矩峰值为44.0 kN·m；E-W模型（即将既有隧道简化成Euler-Bernoulli 梁搁置在Winkler 地基模型上）计算结果明显偏大，桩基峰值位移为16.4 mm，弯矩峰值为77.7 kN·m。其原因在于本文采用的Kerr 地基模型更能反映实际工程中桩-土相互作用机理；此外，Winkler 地基模型缺乏考虑土体剪切作用，其计算数值会明显偏大。与本文方法的退化解相比较，GEPAN 数据[6]的最大桩身水平位移为9.0 mm，最大弯矩为57.8 kN·m，很显然本文方法计算结果更加符合监测GEPAN数据。

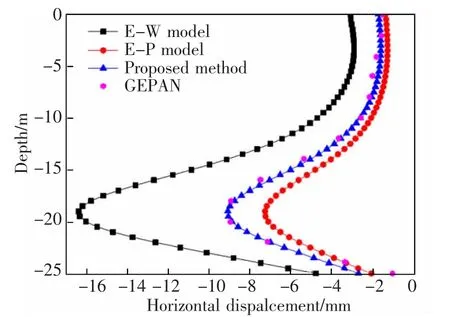
图5 桩基位移与GEPAN 数据对比图Fig.5 The comparison between calculated results of pile displacemont and GEPAN data

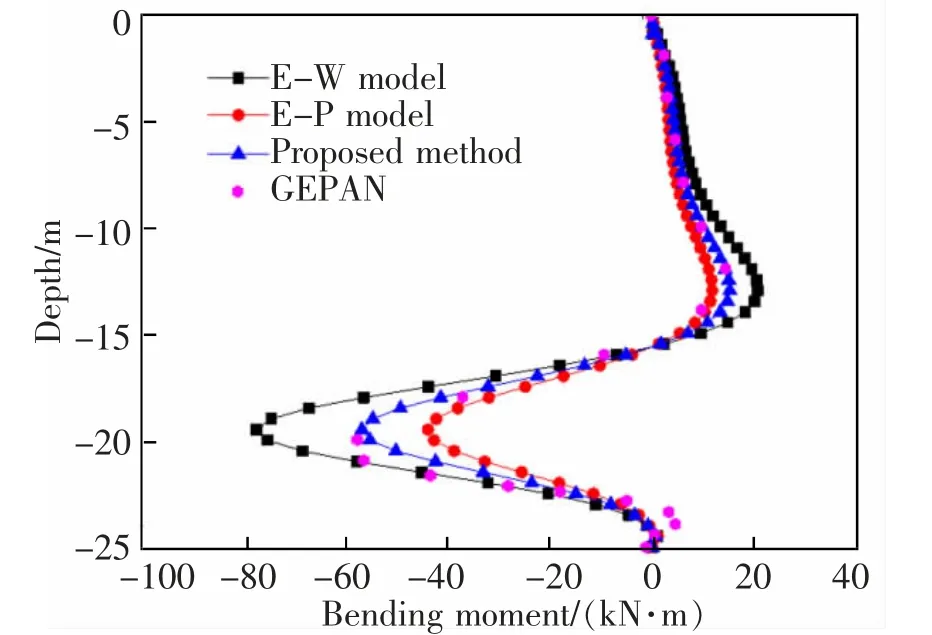
图6 桩基弯矩与GEPAN 数据对比图Fig.6 The comparison between calculated bending moment and GEPAN data

由图5 还可以看出：桩身水平位移变化曲线沿桩基深度呈现出先增大后减小的分布形式，其最大位移值出现在位于隧道开挖轴线埋深附近。图6 可以看出：桩身弯矩变化曲线沿桩基深度呈现出两道鼓肚子的分布形式，其最大负弯矩值出现在位于隧道开挖轴线埋深附近，且明显大于桩基最大正弯矩值。故桩身处和隧道埋深相当的深度应加强桩基应力变形的监测，以保证危险截面的安全性。

3 参数分析

考虑到隧道开挖引起邻近桩基水平位移与几个关键参数之间的关系，建立如下工程案例：隧道埋深H=20 m，隧道半径R=3 m，地层损失率ε0=1%；桩基的计算参数：D=1 m，L=25 m，Ep=30 GPa；桩-隧水平距离x=5 m；土体相应参数：泊松比v=0.33；模量Es=24 MPa。基于所述工程案例进行不同桩-隧相对位置关系、地层损失率、隧道埋深对桩基受力变形影响进行参数分析。

3.1 桩-隧相对位置

桩-隧位置改变时既有桩基受到盾构开挖作用后水平位移变化曲线见图7。由图7 可知，随着桩基远离既有隧道，桩身最大水平从7.23 mm 减少到3.12 mm 且呈现出非线性减小的过程，桩基水平位移峰值发生位置随桩-隧水平距离的增大越来越接近地表。这是因为桩基越远离隧道，隧道开挖对桩基的影响越小，而两者距离较大时，隧道开挖引起桩顶处的土体自由位移最大，显然桩顶处水平位移响应最大。

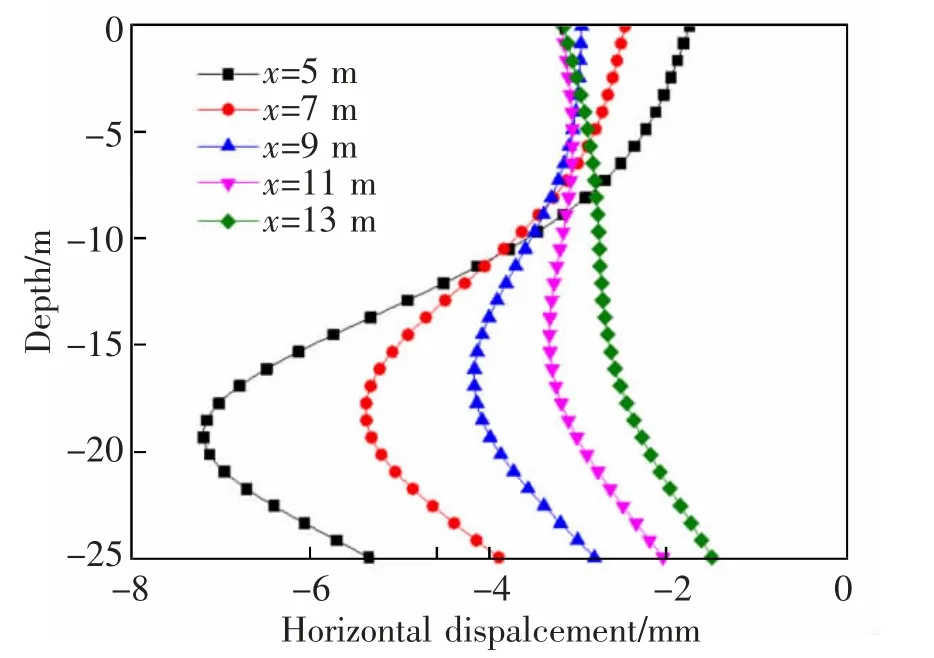
图7 桩-隧水平距离变化时桩基水平变形Fig.7 The pile horizontal deflection in different horizontal distance between pile and tunnel

3.2 地层损失比

地层损失比是指盾构施工过程挖土土体体积与建成隧道体积之比，为了进一步探求地层损失比对邻近桩基水平位移的影响，图8 为地层损失比改变时既有桩基受到盾构开挖作用后水平位移变化曲线。由图8 可知，地层损失由0.5%增加到2.5%的过程中，桩基水平位移逐渐增大，从一开始的3.60 mm线性增大至18.01 mm。由Loganathan[6]公式可知，桩基处土体自由位移随地层损失率的增大而线性增大，随后土体自由位移会被转化成附加应力施加在既有桩基上，此时土中桩基便受到线性增大的附加应力作用，最终使得桩基水平位移也会随之线性增大。

3.3 隧道轴线埋深

隧道轴线埋深改变时既有桩基受到盾构开挖作用后水平位移变化曲线见图9。由图9 可知，隧道埋深从17 m 增加到21 m 时，桩基水平位移从6.83 mm 增加到7.72 mm，可见桩基水平变形响应会随隧道埋深增大而增加。

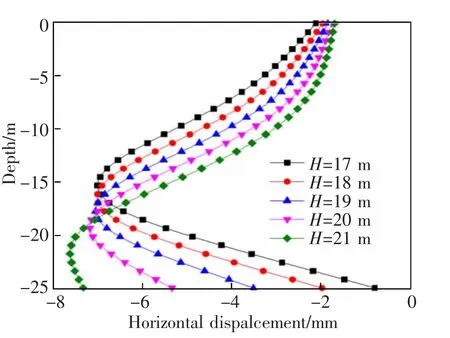
图9 隧道埋深变化时桩基水平变形Fig.9 The pile horizontal deflection in different depth of tunnel axis

4 结论

1）相比于既有理论的半解析解计算结果，本文计算方法更加符合有限元数据。

2）增大盾构隧道的埋深会引起桩基最大水平位移增大，同时会使得桩基水平向最大变形位置深度增大；增大地层损失率会造成邻近桩基水平位移线性增大；桩-隧水平距离的增大会引起桩基水平位移的减小，且会导致桩身产生最大位移埋深减小。