农用旋转机械圆度误差稳定性影响研究*

李 铮 ， 李 冰 ， 高宇星 ， 苏来博 ， 徐武彬

（1.广西科技大学机械与汽车工程学院，广西 柳州 545006；2.广西土方机械协同创新中心，广西 柳州 545006）

0 引言

由于转子系统制造误差存在的客观性，文献[4]和文献[5]使用有限差分法求解存在圆度误差的转子动力学模型，求解油膜力、轴心轨迹以及系统临界转速。考虑尺寸和形位误差及轴瓦表面弹性变形量的影响，使用三维形状误差模型取代二维模型分析误差滑动轴承性能[6-10]。

油膜力是造成轴承转子系统非线性化的主要因素，同时对转子系统动静态特性和运行稳定性产生重要影响。在求解油膜力表达式时，Yaser Bastani等[11]将修正函数应用于无限长（IL）或无限短（IS）的力模型，并通过数值方法求解二维雷诺方程逼近有限长轴承的油膜力计算表达式，预测系统在静态和不平衡载荷下的稳态行为。数值方法求解油膜力是目前研究转子动力学特性的主要方法，但其计算时间长、工作量大的缺点明显不能适应快速求解油膜特性的要求。因此，Dimitris Sfyris 等[12]将雷诺方程拆分为四个线性常微分方程，并与边界条件一起构成四个二阶非恒定系数的线性常微分方程。使用变量分离的方法将雷诺方程的解变换为一组特解和通解的加法和乘法形式进行近似解析解求解。张永芳和黑棣等[13-14]在分离变量的基础上结合变分原理将有限长和无限长径向滑动轴承油膜压力用其轴向和周向分离函数的乘积表示，求得油膜力近似解析解来提高计算效率。

本文利用无限短轴承模型假设建立误差滑动轴承模型，采用分形理论分离误差曲面各阶弦波特征，对其误差特征进行频域范围内的重构，建立三维误差模型。根据计入误差后的油膜厚度表达式进行油膜润滑特性近似解析解计算，研究了制造误差对油膜厚度、油膜压力和承载力的影响。

1 误差转子模型

考虑制造误差状态下的径向滑动轴承模型如图1 所示。其中，R为轴承半径，r为轴颈半径，C为轴承半径间隙，Ob为轴承中心，Oj为轴颈中心，e为偏心距，θ为周向位置角，ω为转子角速度，W为稳定载荷，δ为轴颈中心偏位角，h为实际油膜厚度。

图1 误差滑动轴承模型

在稳定载荷作用和无限短轴承模型假设下，假设油液为不可压缩的层流状态，并忽略温度变化所引起的油液黏度变化，则Reynolds方程可简化为：

为便于计算，引入无量纲变量对公式进行无量纲化：

式中，θ为无量纲周向坐标，λ为无量纲轴向坐标，H为无量纲油膜厚度，p为油膜压力，τ为无量纲时间。

共享经济最早于1978年由美国德克萨斯州立大学两位社会学教授率先提出，在近五年随着互联网的快速发展而逐渐兴起，其主要特点是通过由第三方创建的、以信息技术为基础的平台为最终的需求方和供给方提供服务连接。共享型人力资源是伴随互联网和共享经济的发展而生的，当前对共享型人力资源的研究都是与互联网和共享经济相关联。

代入得无量纲润滑方程：

式中，P为无量纲油膜压力。

2 误差模型建立

分形参数法将误差信息通过FT（Fourier Transform）变换分析分离误差曲面各阶弦波特征，并进行频域范围内重构[15-16]。其中，重要的假设是曲面上任意点的变动（即产生的误差）服从正态分布。在假设情况下对误差曲面使用FT 变换，提取其前N阶主要曲面误差成分建立三维制造误差模型，然后对FT 变换进行逆变换，重构包含误差成分的曲面信息。将其引入到误差轴承转子模型得到轴承转子系统三维制造误差模型表达式：

式中，Ai为第i阶频率曲面幅值（i=1,2,...,N），N为公差数量级内包含的曲面数，fθ,i和fz,i分别为第i阶曲面沿周向方向和轴向方向的频率，φi为第i阶曲面成分初始相位角。

在无限短轴承假设情况下，轴向方向的误差对几何特征的影响可忽略不计，故三维制造误差模型表达式可进一步简化：

根据轴承几何结构图，普通油膜厚度表达式为：h0=C+ecosθ。当仅考虑轴颈形位误差对油膜压力影响的情况时，需要计入轴颈误差值h1。因此，考虑误差影响的油膜厚度表达式为：

代入公式（5）得：

则存在误差时油膜厚度无量纲表达式为：

将油膜厚度表达式代入到短轴承假设条件下的Reynolds 方程（1）中，得到含有制造误差的Reynolds方程表达式：）

将式（8）的等式两端二次积分得到误差轴承转子系统油膜压力表达式：

油膜承载力作为判别滑动轴承承载能力大小的重要参数，其计算方法主要是对轴承周向和轴向油膜压力分布的积分，通过上述油膜压力分布曲线，将油膜压力分布代入油膜承载力表达式，求得周向和轴向油膜承载力Fx和Fy：

式中，L/D为轴承结构长径比，θ1和θ2分别为油膜起始角和终止角。

3 误差对静态特性参数的影响

根据以上对于转子轴承系统的误差模型，对基于短轴承假设的相关轴承几何参数进行求解运算，误差轴承几何参数如表1所示。

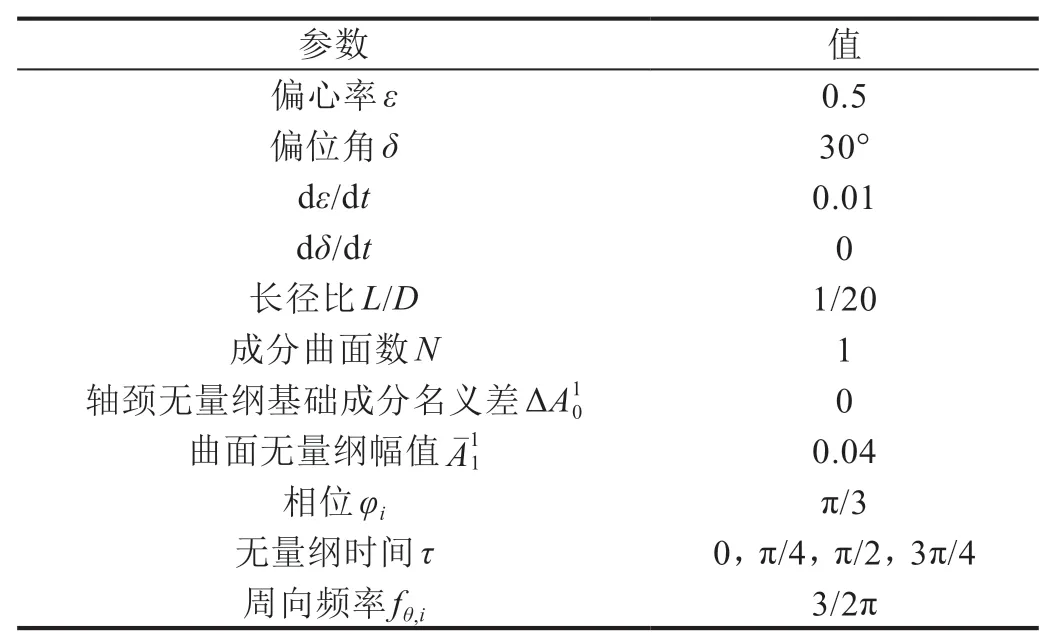
表1 误差轴承几何参数

按照表1 中的几何参数进行误差轴承的油膜压力求解，将其代入考虑存在轴颈误差时的油膜厚度无量纲表达式（7）及误差轴承转子系统油膜压力表达式（9）中，取得在误差影响下不同运行时间的油膜厚度变化图和油膜压力变化曲线。为探究误差对于油膜厚度的影响，对比分析理想轴承油膜厚度H0、油膜压力P0与存在制造误差情况下的油膜厚度H、油膜压力P在不同无量纲运行时间的变化曲线。

对比发现，油膜厚度在误差存在时整体曲线变化趋势具有一致性，但在制造误差影响下的油膜厚度值会随着理想油膜厚度值发生小范围波动，特别是当达到油膜压力的较大值时油膜厚度产生的变化更明显，油膜厚度变化曲线如图2 所示。

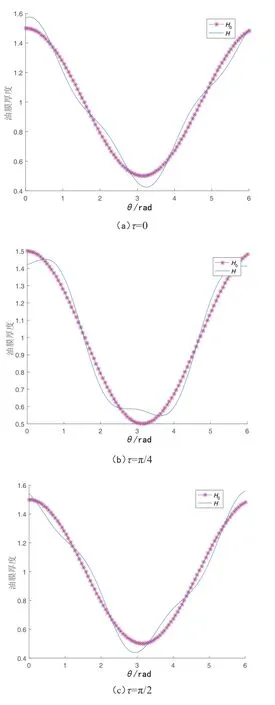
图2 有无误差情况下无量纲油膜厚度随θ 变化曲线

同时，曲线呈现周期性变化，符合轴颈旋转运行时的周期运转特征。通过将受误差影响的承载力Fx和Fy与无误差影响的承载力F0x和F0y进行对比发现，无限短轴承假设模型情况下，轴颈误差对x方向的承载力影响强于y方向。

此外，随着转子系统运行过程中产生新的油膜力、外载荷作用及磨损等因素，轴颈在运行过程中会产生新的偏心率和偏位角。将不同偏心率代入上述考虑圆度误差的油膜润滑理论公式计算相关油膜厚度、油膜压力和承载力等转子运行稳定因素，结果发现当偏心率从0.1 变化到0.5 时，带有误差的油膜压力相较于理想轮廓轴承在运行时间范围内会产生较大的压力波动变化。同时，随着偏心率的增大，压力幅值变化增大。

4 结论

1）建立了考虑制造误差状态的径向滑动轴承模型，并利用短轴承理论建立存在轴颈制造误差情况下的润滑Reynolds 方程。

2）通过分形理论，将扫描得到的轴颈三维误差进行FT（Fourier Transform）变换分析，分离误差曲面各阶弦波特征，并进行频域范围内重构，将其引入到误差轴承转子模型中建立轴承转子系统三维制造误差模型表达式。

3）结合循环边界条件，研究并分析轴颈制造误差对油膜厚度和油膜压力变化的影响。在误差轴颈运行位置角变化范围内，油膜厚度在油膜压力较大值时会产生明显波动，并呈周期性变化；制造误差对油膜压力波动和方向承载力影响较大，且随着偏心率的增大，油膜压力幅值变化增大。