一种基于改进布谷鸟算法的极值搜索控制方法及应用*

黄政雨 ， 白玉婷

（1.杭州电子科技大学经济学院，浙江 杭州 310018；2.黔南民族师范学院计算机与信息学院，贵州 黔南州 558000）

0 引言

化石燃料的减少和环境污染的加剧是当今世界面临的重要发展问题[1]。太阳能的利用具有成本低、环境友好、零碳排放和自然资源丰富等优点，受到广大科研人员的青睐[2]。由于不确定的环境影响，太阳能电池功率-电压（P-V）曲线是非线性的，需要一个最大功率点跟踪（MPPT）控制器确保在任何环境下太阳能电池都保持最大功率工作[3]。

极值搜索控制方法（ESC）一般针对不确定复杂动力学模型，通过动态调整动力学参数和反馈控制实现这些系统的最优控制[4]。太阳能光伏系统所处外界环境复杂，最优稳态模型不确定，传统最优控制难以应用，因此可采用极值搜索控制方法实现动态环境下的最大功率点跟踪（MPPT）控制[5]。

传统MPPT 控制技术，例如增量电导法（INC）、扰动和观测方法（P&O）基于梯度下降原理，无法区分局部最优和全局最优值[6]。基于智能优化的MPPT控制技术，例如蚁群算法（ACO）、灰狼算法（GWO）等由于其随机性的特点，动态性能参差不齐且系统振荡过多，工业应用困难[7]。课题组研究了一种基于改进布谷鸟算法（CS）的极值搜索控制方法，并进行了仿真实验以验证方法性能。首先，介绍控制系统动力学模型；其次，介绍基于改进布谷鸟算法的极值搜索控制方法；再次，进行实验测试；最后，对全文进行总结。

1 太阳能光伏系统动力学模型

一般的太阳能光伏系统由三个部分组成，即太阳能电池、DC-DC 转换电路和MPPT 控制器。太阳能电池可以通过电流源、二极管和电阻进行建模[8]，数学模型如式（1）所示：

式中，Iph(t)为太阳能电池发电产生的动态电流，Is为二极管饱和电流，V(t)为太阳能电池输出电压，Rs为串联电阻，A、Vt为电路理想系数，可视为常数。DC-DC 斩波电路数学模型已有研究人员研究，如式（2）所示[9]：

综上，可得太阳能光伏系统动力学模型，如式（3）所示：

式中，f、J均为系统状态变量、输出变量的平滑映射函数，其中J为不确定函数。而且由于能量守恒定律限制，该系统为自稳定系统且对于任意的J皆存在u*，使得y=y*，y*≥y(t)。

2 基于改进布谷鸟算法的极值搜索控制方法（ICS）

布谷鸟搜索算法通过模拟布谷鸟的寄生育雏习性有效求解优化问题[10]。布谷鸟采用一种迭代方式由一个巢随机飞向另一个巢，寻找安全孵化幼崽概率最高的巢穴。如果宿主发现了布谷鸟蛋，则会将其扔掉或者弃巢。布谷鸟算法利用Levy 飞行实现布谷鸟由一个巢飞向另一个巢的迭代，如式（4）所示：

式中，i是迭代次数，k=1,2,…,ss是当前搜寻群体中的个体排序，ss是搜索群体大小，α是搜索步长，u和v是基于均匀分布的随机矩阵，如式（5）所示：

其中，u和v的方差如式（6）所示：

每一次迭代后布谷鸟蛋均有被宿主发现的危险，被发现概率为p。若被发现，则布谷鸟会飞向随机巢并重新迭代。为加快算法收敛速度，改进布谷鸟蛋被发现后的迭代算法，布谷鸟不飞向随机位置而继续向当前全局最优dbest迭代，如式（7）所示：

这样就使得算法向当前最优值更快速移动，提升了算法的收敛速度。假设系统扰动响应速度慢于系统控制器输入调整速度，系统输入调整速度慢于系统输出响应速度，则在调节时间内，可认为系统外界扰动为常值，在该时间尺度下系统模型为定长确定模型。以该时间尺度为采样和控制调节时间，在该时间尺度利用改进布谷鸟算法实现优化控制，则可得到系统离散控制率u(k)。

由于物理系统为连续系统，而改进布谷鸟算法为离散算法，因此需将离散的布谷鸟算法转变为连续系统的控制器。基于零阶保持器的原理，在采样的两个时刻之间，控制输入保持不变，则可得离散-连续的极值搜索控制方法，如式（8）所示：

3 数值仿真

本文利用MATLAB 建立了太阳能光伏系统动力学模型，该模型模拟环境温度为20 ℃，PWM 频率设置为100 kHz，采样频率为0.001 s，模拟失配条件下的光伏发电系统输入PWM 信号占空比到输出功率的平滑映射函数。该函数呈现多峰特性，具有4 个极点且最大输出功率为570 W。本文利用Runge-Kutta 方法求该仿真模型的数值解。

实验测试了在相同情况下传统CS 算法和本文提出的ICS 算法的性能，算法仿真结果如图1 所示。传统CS 算法和本文提出的ICS 算法均能找到全局最优值，但本文提出的ICS 算法找到的全局最优值为559.74 W，传统CS 算法找到的全局最优值为522.04 W，且在稳定后传统CS 算法存在小幅度振荡，而本文提出的ICS 算法不存在稳态振荡，因此本文提出的ICS 算法稳态性能远优于传统CS 算法。传统CS 算法在0.078 3 s 后收敛，而本文提出的ICS 算法在0.025 5 s 处实现收敛，本文提出的ICS 算法调节时间三倍优于传统CS 算法。传统CS 算法存在大幅振荡10 余次，小幅振荡20 余次，而本文提出的ICS 算法仅存在大幅振荡两次，小幅振荡一次，算法动态性能远优于传统CS算法。

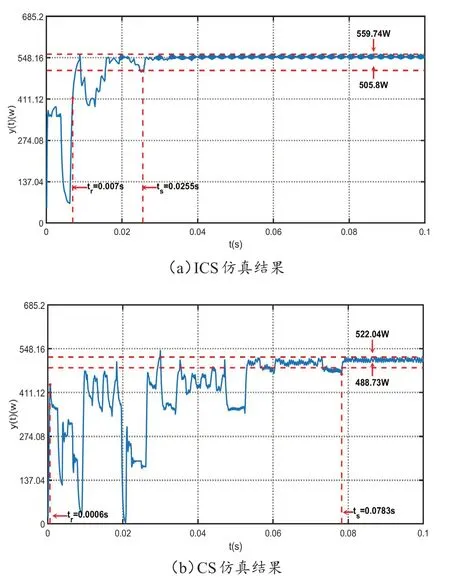
图1 算法仿真结果

综上所述，本文所提出的ICS 算法在仿真研究中动态性能和稳态性能远优于传统CS 算法，其在调节时间、振荡水平和极值搜索能力等方面均性能优越。

4 结论

首先，基于太阳能光伏系统的物理机理和控制电路，课题组提出了一种动力学模型以解释和概括太阳能光伏系统；基于极值搜索控制机理，课题组提出了基于时间尺度的假设，并验证了太阳能光伏系统极值搜索的可能性。

其次，课题组提出了一种基于改进布谷鸟算法的极值搜索控制方法，在采样时间内完成系统的最优控制，并基于离散-连续控制方法实现连续动态太阳能光伏系统的最优控制。该方法结构简单，动态性能和稳态性能卓越，且实现了离散-连续控制转换，可用于数字控制电路。

最后，课题组通过数值仿真将提出的算法在失配条件下与传统CS 算法进行比较，以验证算法追踪全局最大功率点（GMPP）的能力。结果显示，课题组提出的ICS 算法可以非常精准地找到和追踪GMPP，其动态性能和稳态性能均远优于传统CS 算法，其中算法稳态振荡全部消除，算法找到的极值输出功率也大于传统CS 算法，算法调节速度提升了约两倍，算法振荡水平大幅降低。