静态混合器内分散相混合性能数值模拟

祝鑫 吕汪洋 王刚强

摘要：为了解决熔体纺丝过程中由于在线添加颗粒引起的熔体品质降低与混合性能变差的问题，采用有限元法针对不同结构与工艺参数的静态混合器进行了建模与求解，得到了后处理结果。同时，为了定量表征其混合性能，采用示踪粒子技术求解了分离尺度、停留时间分布以及最大剪切应力的累积概率函数并对其进行统计学分析。结果表明：长径比由1升高到1.75时，管道内压力降由0.52 MPa上升至0.62 MPa，分离尺度差异不大，停留时间峰值逐渐减小，最大剪切应力大于5 kPa的概率提升到78%。进口流量从2×10-5 m3/s提升到8×10-5 m3/s，熔体的压力降从0.52 MPa上升至2.00 MPa，分离尺度变化较小，停留时间的峰值变高，最大剪切应力大于10 kPa的概率达到83%。

关键词：静态混合器；熔体纺丝；有限元法；示踪粒子技术；长径比；进口流量；最剪切应力

中图分类号：TQ342+.2

文献标志码：A

文章编号：1009-265X（2023）02-0063-09

化纤在进行纺丝前，通常需要将已经熔融的聚合物熔体输送进入纺丝箱里。而在实际的纺丝过程中通常不是直接将单一的聚合物熔体进行纺丝，需要加入含有功能性的颗粒物，用于制备功能性纤维，但由于加入颗粒产生的团聚现象使得颗粒无法在纤维上均匀分布［1］。针对实际化纤工业生产中改善颗粒物分散的需求，需要使用静态混合器作为用来改善熔体与分散相颗粒的混合性能。静态混合器内的分散相在熔体内的分布与分散直接决定纤维的功能性好坏。

国内外学者对静态混合器进行了大量研究，早期主要以实验为主。Middleman等［2］使用Pentax相机对静态混合器进行拍照，并用Sauter平均直径来表示液滴粒径的变化情况，但是这种方法存在一定的缺陷，它無法反映由于液滴重合产生的测量误差。随着技术的发展，各种先进的测量技术被应用于静态混合器测量中。Karoui等［3］利用激光诱导荧光技术研究了在Sulzer SMV静态混合器出口处的浓度，并利用统计学原理分析其平均值和均方根，其结果表明两种流体的速度比、元件的数量等参数均会影响流体的混合均匀程度。Jegatheeswaran等［4］根据两种不同流体电导率的差异，运用电阻层析成像技术做出层析图，与CFD中压力降、分散相流体的浓度分布、混合指数云图对比来验证流体的混沌性能，揭示了由于少组分流体速度增加使得流体变形程度增加，扩散能力增强的机理。

但是，由于静态混合器几何形状的复杂性，使得静态混合器的实验测量存在较大的测量误差。随着有限元计算方法的出现，不少学者开始用数值模拟的方法来替代传统的实验测量，减少由于混合器结构形状的复杂性导致测量的偏差。王宗勇等［5］利用Fluent软件与群体平衡模型（PBM）耦合的方法，对工艺参数修改，发现液滴破碎主要原因是由静态混合器的分流和改向引起，而且液滴粒径的大小是由元件数与流体本身的性质共同决定，具有互补作用。张春梅等［6］应用Fluent软件模拟了不同排列方式的元件的浓度场及压力降大小，研究发现异旋交叉排列的方式能获得最大程度的混合，并考虑压力降的影响，得出同旋叉排，长径比为2的静态混合器综合性能更好。Haddadi等［7］设计了一种新型的静态混合器，与Kenics、SMX、Komax3种混合器进行对比，并用Fluent软件计算这4种静态混合器的内部流场及混合评价指标，最终CFD表明，新型的静态混合器具有更好分布混合性能与分散混合性能。Meijer等［8］模拟了不同静态混合器的浓度场，并总结了不同静态混合器出口处的条纹分布图像。

基于前者对静态混合器的理论与实验的探究，发现在化纤工业领域对静态混合器的研究较少，而静态混合器作为在纺丝线路中的重要元件，探索静态混合器内熔体与分散相的混合性能能很好地保证纺丝过程中分散相在纤维上均匀分布与分散，使纤维获得更好的功能性。研究过程中主要改变静态混合器的结构参数和物料的输送速率，探讨工艺参数对熔体流动和混合性能的影响，得到具有更好的混合性能的工艺参数组合。

1数值模拟

1.1前处理

本文模拟的静态混合器为企业实际使用的混合设备。根据相关研究结果，静态混合器在旋转角为120°时具有更好的混合性能以及良好的流动性能［9］。因此，本文使用120°的旋转角元件的静态混合器进行分析，通过改变长径比和进口流量来观察模拟结果的差异。静态混合器尺寸如表1所示。

静态混合器的几何模型主要在Solidworks软件中完成，如图1（a）所示。在建立好静态混合器的几何模型之后，需要进行抽取流体域，流体域是需要去计算求解的部分，因此，在获得了流体域模型之后，对流体域进行网格划分，网格划分使用ANSYS Meshing完成，网格划分模型的三维图如图1（b）所示。

1.2数值求解

对于静态混合器内的熔体流动性能，可以用熔体的连续性方程和本构方程描述，如式（1）－式（3）：

Δ·v=0（1）

-Δp+Δ·τ=0（2）

τ =2ηD（3）

式中：v为速度矢量，p为压力，τ为应力张量，η为表观黏度，D为形变速率张量。在该模型中，需作出如下假设：

a）整个流动系统为定常流动状态，且熔体不可压缩。

b）熔体的流动填充整个型腔，且熔体内部是连续的，即不存在气泡等。

c）熔体受到的黏性力要远大于惯性力与重力，因此不考虑惯性力与重力。

由于模拟的材料为聚合物的熔体，其黏度与剪切速率并非线性，因此该材料为非牛顿流体，黏度模型用Bird-carreau模型来描述，如式（4）：

η =η∞+（η0-η∞）（1+（λγ）2）n-12（4）

式中：η∞为剪切速率无穷大时的黏度；η0为表观黏度；λ为松弛时间；n为非牛顿系数；γ为剪切速率；材料参数的设置参考文献［9］。

选择入口为流量入口，入口流量将作为控制变量，这里只给出在改变长径比时的流量，其大小为2×10-5m3/s；管道的出口为压力出口，出口处压力为0（这个出口是整个管道的出口）；其余的面均设置为壁面，壁面处无滑移。本文使用Polyflow软件来完成计算求解，利用有限元方法，求解连续性方程和本构方程，残差设置为10-3。

1.3示踪粒子技术

采用示踪粒子的方法对其分布与分散性能进行表征，示踪粒子数量为3000，示踪粒子在三维流场内速度场可表示为式（5）：

u=u（x，t）（5）

式中：x表示示踪粒子的位置信息，t表示时间，所以示踪粒子的轨迹可表示为式（6）：

dxdt=u（x，t）（6）

示踪粒子的轨迹的求解算法为四阶Runge-Kutta法，在给定初始位置x=x（x0，y0，z0）的情况下，通过对速度积分，获得一个比较精确的示踪粒子的下一个信息，以此往复。

1.4网格无关性验证

为了保证模拟结果的准确性，需要对模拟的结果进行网格无关性检验，在保持几何模型相同，网格划分的方式一致的情况下，修改静态混合器的网格尺寸，得到不同数量的网格模型。取点（0.01，0，0.01）和（0.01，0.24，0.01）连接两点做参考线a-a′，计算轴向距离与速度的关系。由图2可知，这些网格模型的曲线总体趋势是大致相同的，但3万的网格模型的模拟结果与其他的网格模型结果有一定的差异，而34万，153万，198万这些网格模型的模

拟结果差异较小，模拟结果之间的误差均小于10-3 m/s，而网格數量的增多会导致计算量的增大，计算时间变长。参考线a-a′上轴向距离与速度的关系如图2所示，由图2可以看出，当网格数量达到34万以上后，模拟结果的数值将不再发生大的变化。因此，在保证模拟结果没有太大差异的情况下，选择34万及以上数量网格比较合适。

2结果与讨论

2.1流动性能

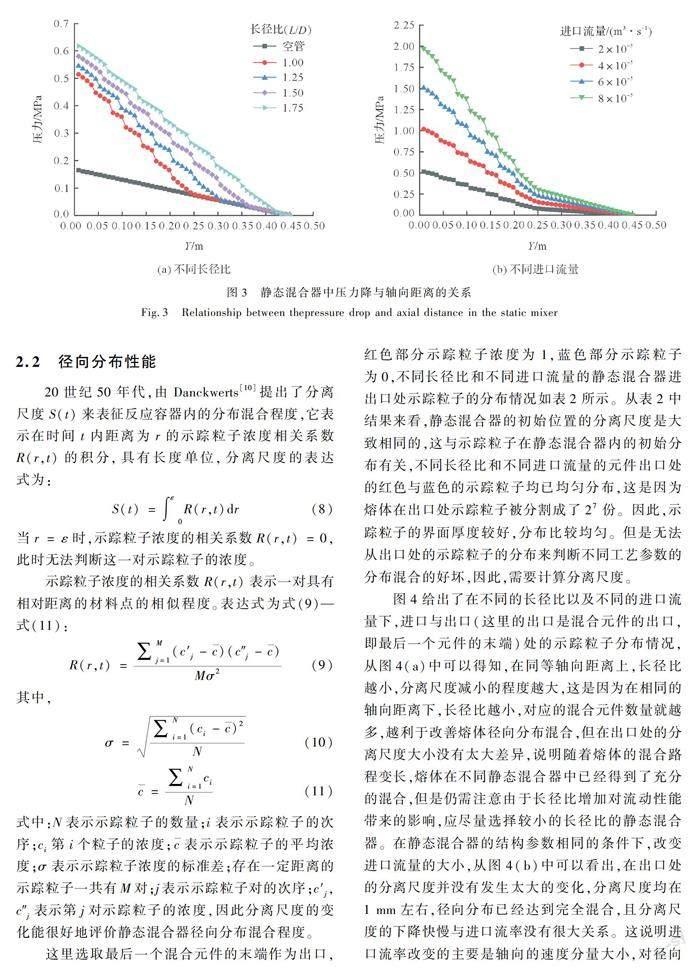
在模拟熔体压力降过程中，取点（0.01，0，0.01），（0.01，0.45，0.01）并连接成线段，选取该线段作为参考线c-c′，选取了空管与不同长径比（1.00，1.25，1.50，1.75）的静态混合器作对比，参考线上的压力降如图3所示，不同的混合元件的压力降有一定的差异，长径比大的静态混合器的混合段压力降会更大。先定义阻力系数Z，如式（7）：

Z=ΔpΔp0（7）

式中：Δp为静态混合器的压力降大小，Δp0为空管压力降大小。阻力系数的大小反映了该混合器对熔体流动性能的影响程度。参考线上的压力降曲线如图3所示，发现管道内的阻力系数为3～4左右。不同的静态混合器的压力降差异在0.2 MPa以内，这是因为在改变长径比的过程中，由于管径不变，增大长径比即增长混合元件的长度。增加混合元件的长度即增大了熔体的流动阻力，压力降随之增大。

在静态混合器的各个结构参数相同的情况下，控制物料流量的大小，不同的体积流率的压力降也有所不同。随着体积流率的增加，静态混合器的压力降开始上升，根据压力降的计算公式：ΔP=f′·La·ρu22，u=4Vπd2，以及其他条件一定的情况下，可以得知ΔP∝V2，进口体积流率的增大会使得压力降迅速上升，其对压力降的影响效果要大于长径比对压力降的影响效果。

在图3中，不同工艺参数的静态混合器的压力降曲线出现了阶梯式下降，这是由于混合元件的阻力作用，使熔体在经过混合元件时产生了能量的损耗，而空管由于没有混合叶片的阻力作用，因此不存在压力骤降，其压力曲线表现为一条平直下降的直线。不同工艺参数的压力骤降的程度也有差别，这主要是因为，不同的工艺参数的静态混合器产生的能量损耗也是有差异的。

2.2径向分布性能

20世纪50年代，由Danckwerts［10］提出了分离尺度S（t）来表征反应容器内的分布混合程度，它表示在时间t内距离为r的示踪粒子浓度相关系数R（r，t）的积分，具有长度单位，分离尺度的表达式为：

S（t）=∫ε0R（r，t）dr（8）

当r=ε时，示踪粒子浓度的相关系数R（r，t）=0，此时无法判断这一对示踪粒子的浓度。

示踪粒子浓度的相关系数R（r，t）表示一对具有相对距离的材料点的相似程度。表达式为式（9）—式（11）：

R（r，t）=∑Mj=1（c′j-c）（c″j-c）Mσ2（9）

其中，

σ=∑Ni=1（ci-c）2N（10）

c=∑Ni=1ciN（11）

式中：N表示示踪粒子的数量；i表示示踪粒子的次序；ci第i个粒子的浓度；c表示示踪粒子的平均浓度；σ表示示踪粒子浓度的标准差；存在一定距离的示踪粒子一共有M对；j表示示踪粒子对的次序；c′j，c″j表示第j对示踪粒子的浓度，因此分离尺度的变化能很好地评价静态混合器径向分布混合程度。

这里选取最后一个混合元件的末端作为出口，红色部分示踪粒子浓度为1，蓝色部分示踪粒子为0，不同长径比和不同进口流量的静态混合器进出口处示踪粒子的分布情况如表2所示。从表2中结果来看，静态混合器的初始位置的分离尺度是大致相同的，这与示踪粒子在静态混合器内的初始分布有关，不同长径比和不同进口流量的元件出口处的红色与蓝色的示踪粒子均已均匀分布，这是因为熔体在出口处示踪粒子被分割成了27份。因此，示踪粒子的界面厚度较好，分布比较均匀。但是无法从出口处的示踪粒子的分布来判断不同工艺参数的分布混合的好坏，因此，需要计算分离尺度。

图4给出了在不同的长径比以及不同的进口流量下，进口与出口（这里的出口是混合元件的出口，即最后一个元件的末端）处的示踪粒子分布情况，从图4（a）中可以得知，在同等轴向距离上，长径比越小，分离尺度减小的程度越大，这是因为在相同的轴向距离下，长径比越小，对应的混合元件数量就越多，越利于改善熔体径向分布混合，但在出口处的分离尺度大小没有太大差异，说明随着熔体的混合路程变长，熔体在不同静态混合器中已经得到了充分的混合，但是仍需注意由于长径比增加对流动性能带来的影响，应尽量选择较小的长径比的静态混合器。在静态混合器的结构参数相同的条件下，改变进口流量的大小，从图4（b）中可以看出，在出口处的分离尺度并没有发生太大的变化，分离尺度均在1 mm左右，径向分布已经达到完全混合，且分离尺度的下降快慢与进口流率没有很大关系。这说明进口流率改变的主要是轴向的速度分量大小，对径向速度分量的大小影响不大，因此对径向分布混合的影响是较小的。此外还可以看出，分离尺度的下降主要发生在前两个混合元件，在后面4个元件中分离尺度的变化并没有那么大。这主要是因为流体在低雷诺数下运动时，前面两个元件中流体的速度场变化较大，熔体内的示踪粒子在流场中的分布更加均匀，而到第3个元件时，速度场趋于稳定，因此分离尺度的变化较小［11］。

2.3轴向分布性能

停留时间分布是由于在结构设计时的缺陷，以及物料的回流，返混等等因素，使得熔体在流动的过程中微小的熔体单元产生了不同的速度分布，则形成了停留时间的差异。其定义为，在定常连续流动系统中，由t=0时刻流入反应容器中的流体，在出口位置示踪粒子停留了t到t+Δt的流体质点所占的分率为E（t）dt，对其进行积分，则∫t0E（t）dt表示流体质点停留时间的密度函数。密度函数有如下性质，如式（12）：

∫+∞0E（t）dt=1（12）

停留时间分布是示踪粒子沿管道流动产生的差异，它很好地反应了管道内的流体沿轴向的分布程度。

选取不同长径比的静态混合器，并计算其混合元件出口处的停留时间分布，出口处的停留时间分布图如图5（a）所示。由图5（a）可以看出，随着长径比的增大，停留时间分布的峰值逐渐向时间轴正方向偏移，停留时间分布的峰宽逐渐变大，峰值逐渐变小，即物料在管道的停留时间变长，这说明有更多的物料的流出的时间更长了，这有利于熔体在轴向上的分布混合，因此应当考虑增大静态混合器的长径比，来改善静态混合器的轴向分布混合性能，提升熔体的品质。而由图5（b）可知，随着体积流率的减小，峰值向右偏移，停留时间分布曲线的峰宽变得更宽，峰值更小，出峰的时间更长了，因此减小进口流量能很好地改善轴向混合性能。这主要是因为进口流量的方向与进口流量的平面垂直，熔体的流动主要影响的是熔体在轴向上的速度分量，即对轴向的分布影响更大，而且，体积流率为2×10-5m3/s与8×10-5m3/s的峰值相差是较大的，这说明体积流率对停留时间的影响更大。因此，较小的体积流率能更好地改善轴向分布混合。

2.4分散性能

20世纪90年代由Rwei等［12-13］提出，炭黑在聚合物基材料中的分散过程中，其分散机理主要为团聚体在剪切流场中发生剥蚀和破碎，而剥蚀与破碎的机理主要是由于团聚体在流场中受到的应力达到临界值，团聚体产生小粒径颗粒的脱落和团聚体自身破碎形成小团聚体而产生。因此，所受到的剪切应力越大，分散效果越好。判断熔体的分散混合程度主要是判断示踪粒子所受到的最大剪切应力，这里引用了概率密度函数与累积概率函数来描述示踪受到剪切应力的概率，如式（13）、式（14）所示：

F（x）=P（|x≤a|）（13）

f（x）=F（x）x（14）

式中：x为自变量，P（|x≤a|）表示x≤a当时的概率，f（x）是F（x）对x求偏导的结果。

不同长径比和不同进口流量的静态混合器剪切速率的分布情况分别如图6、图7所示。

由图6中可以看出，对于不同长径比的静态混合器，长径比越小，其对应的剪切速率越大，這是因为长径比的减小使混合器叶片的扭曲程度变大了，因此在叶片边缘处径向速度分量变大，剪切速率变大，不过，从数值上看，最大剪切速率变大的程度比较，从长径比1.75到1.00，最大剪切速率只增大了0.12 s-1，但是，由于长径比的增大，混合段长度变

长，长径比更大的混合器将有更多的熔体获得更大的剪切速率，这将使得熔体内的分散相得到更好的分散效果。

从图7中剪切速率云图可以看出，不同体积流率的剪切速度云图的分布没有太大的差异，这主要是因为由于静态混合器的结构是相同的，而熔体的剪切速率的分布是由静态混合器的结构所决定。但是，不同体积流率的剪切速率的大小是有差异的，随着体积流率的增大，熔体的剪切速率也随之增大，熔体的分散性能更好。

最大剪切应力的累积概率函数如图8所示，由图8中可知，长径比为1.75的混合器更靠近内侧，这将有更多的示踪粒子受到更大的剪切应力。取最大剪切应力为5 kPa，不同长径比（1.00，1.25，1.50，1.75）的静态混合器对应的概率值分别为54%，44%，32%，22%，则分别有46%，56%，68%，78%的示踪粒子受到剪切应力大于5 kPa，因此，长径比为1.75的静态混合器有更多的示踪粒子受到了更大的剪切应力，那么它的分散效果也会更好。当最大剪切应力为10 kPa时，体积流率为2×10-5，4×10-5，6×10-5，8×10-5m3/s的静态混合器内的示踪粒子的概率分别为86%，56%，30%，17%，因此，体积流率为2×10-5，4×10-5，6×10-5，8×10-5m3/s的静态混合器内的示踪粒子受到的剪切应力大于10 kPa的概率分别为14%，44%，70%，83%。所以体积流率越大，静态混合器内更多的示踪粒子受到更大的剪切应力的概率越大，熔体处于高剪切的流动状态，因此，熔体内的分散相由于处在高剪切的流场中，使得颗粒团聚体发生剥蚀和破碎的自发性更强。

3结 论

通过对静态混合器进行了数值求解同时还改变了静态混合器的结构参数和进口流量的大小，来讨论工艺参数对聚合物流体流动与混合的影响。在模拟过程中，得出如下结论：

a）在改变叶片长径比的过程中，叶片长径比越大，轴向分布混合性能更好，熔体的分散混合性能好，但压力降变大使得熔体流动性能变差，可以考虑适中的长径比的静态混合器，或者通过增加叶片数量来调整分布混合与分散混合。

b）进口流量减小，熔体的压力降下降，流动性能越好，分离尺度没有发生太大变化，轴向混合性能得到提升，但分散效果变差。因为压力降过高，熔体的品质会下降，结合上述的数据，在能够保证在流动性能不是太差的情况下提升熔体的进口流量，使熔体受到较高的剪切应力可以使熔体具有比较好的分散性能。

c）改变长径比主要是改善静态混合器的分散性能与分布混合性能，改变进口流量主要是改善流动性能与分布混合性能，可以根据这些结论结合实际情况来控制工艺参数，同时，改变进口流量对熔体的流动与混合性能的影响要比改变静态混合器的结构参数影响更大，因此，在实际生产中应更着重关注进口流量的影响。

参考文献：

［1］姜兆辉，李志迎，王婧，等.纳米无机粒子/聚合物共混体系分散机理研究进展［J］.化工新型材料，2015，43（2）：27-29.

JIANG Zhaohui， LI Zhiying， WANG Jing， et al. Research progress on dispersion mechanism of nanopar-ticles/polymer system［J］. New Chemical Materials， 2015， 43（2）： 27-29.

［2］MIDDLEMAN S. Drop size distributions produced by turbulent pipe flow of immiscible fluids through a static mixer［J］. Industrial & Engineering Chemistry Process Design and Development， 1974， 13（1）： 78-83.

［3］KAROUI A， HAKENHOLZ F， LESAUZE N， et al. Deter-mination of the mixing performance of sulzer SMV static mixers by laser induced fluorescence［J］. The Canadian Journal of Chemical Engineering， 1998， 76（3）： 522-526.

［4］JEGATHEESWARAN S， EIN-MOZAFFARI F， WU J. Process intensification in a chaotic SMX static mixer to achieve an energy-efficient mixing operation of non-newtonian fluids［J］. Chemical Engineering and Processing-Process Intensification， 2018， 124： 1-10.

［5］王宗勇，王亮，孟輝波.Kenics型静态混合器内分散相液滴破碎和聚结过程的CFD-PBM数值模拟［J］.过程工程学报，2021，21（8）：935-943.

WANG Zongyong， WANG Liang， MENG Huibo. CFD-PBM numerical simulation on the breakup and coalescence process of dispersed phase droplet in Kenics static mixer［J］. Journal of Process Engineering， 2021，21（8）：935-943.

［6］张春梅，陈豪杰，刘建.元件排列方式对液液静态混合的影响［J］.沈阳化工大学学报，2017，31（4）：360-365.

ZHANG Chunmei， CHEN Haojie， LIU Jian. Influence of element arrangement on liquid-liquid mixing in a static mixer［J］. Journal of Shenyang University of Chemical Technology， 2017，31（4）： 360-365.

［7］HADDADI M M， HOSSEINI S H， RASHTCHIAN D， et al.Comparative analysis of different static mixers performance by CFD technique： An innovative mixer［J］.Chinese Journal of Chemical Engineering， 2020， 28（3）： 672-684.

［8］MEIJER H E H， SINGH M K， ANDERSON P D. On the performance of static mixers： A quantitative comparison［J］. Progress in Polymer Science， 2012， 37（10）： 1333-1349.

［9］赵月，马建平，陈世昌，等.Kenics型静态混合器的结构优化与数值模拟［J］.合成纤维工业，2019，42（2）：74-80.

ZHAO Yue，MA Jianping， CHEN Shichang， et al.Numerical simulation and structure optimization of Kenics static mixers［J］. Synthetic Fiber Industry， 2019， 42（2）： 74-80.

［10］DANCKWERTS P V. The definition and measurement of some characteristics of mixtures［J］. Applied Scientific Research， Section A， 1952， 3（4）： 279-296.

［11］HOBBS D M， SWANSON P D， MUZZIO F J. Numerical characterization of low reynolds number flow in the Kenics static mixer［J］. Chemical Engineering Science， 1998， 53（8）： 1565-1584.

［12］RWEI S P， MANAS-ZLOCZOWER I， FEKE D L. Observation of carbon black agglomerate dispersion in simple shear flows［J］. Polymer Engineering & Science， 1990， 30（12）： 701-706.

［13］RWEI S P， MANAS-ZLOCZOWER I， FEKE D L. Charac-terization of agglomerate dispersion by erosion in simple shear flows［J］. Polymer Engineering & Science， 1991， 31（8）： 558-562.

Numerical simulation of mixing performance of dispersed phase in a static mixer

ZHU Xin， L Wangyang， WANG Gangqiang

（State-Locality Joint Engineering Laboratory of Textile Fiber Material and Processing Technology， Zhejiang Sci-Tech University， Hangzhou 310018， China）

Abstract： Spinning is a process in which polymers are extruded in a certain form to form chemical fibers， which are then processed to make textiles commonly used in daily life. In the process of melt spinning， it is usually necessary to add functional granules into the melted polymer melt， and use a static mixer to improve the mixing effect between the melt quality and dispersed phase particles， so as to prepare functional fiber materials. However， in the actual production process， the dispersion mixing of functional particulate matter is always a difficult problem， particulate matter tends to agglomerate within the polymer melt， and the measurement process of the experiment is complex. Therefore， improving the spinnability of the polymer melt during the spinning process and reducing the agglomeration of particles within the fiber can effectively improve the functionality of the fiber material. In order to solve the problem of melt quality degradation and mixing performance deterioration caused by online particle addition during melt spinning， the finite element method （FEM） was used to model the geometry， mesh， set material parameters and boundary conditions， and calculate the solution for static mixers with different structures and process parameters， and the post-processing results and the pressure drop curve in the flow direction were obtained. Meanwhile， in order to quantitatively characterize its mixing performance， the tracer particle technique was used for analysis， and the cumulative probability functions of separation scale， residence time distribution， and maximum shear stress were obtained by solving the fourth-order Runge-Kutta algorithm， and they were statistically analyzed. The analysis results show that when the aspect ratio is increased from 1 to 1.75， the pressure drop in the pipe rises from 0.52 MPa to 0.62 Mpa， the flow resistance increases， the decreasing speed of the separation scale becomes smaller， but the difference at the outlet is not significant， the peak of residence time gradually decreases， the axial mixing effect is better， the probability of the maximum shear stress greater than 5 kPa is raised to 78%， and the degree of agglomeration of the dispersed phase is reduced. The inlet flow rate is increased from 2×10-5 m3/s to 8×10-5 m3/s， the pressure drop of the melt increases from 0.52 MPa to 2.00 MPa， the flow resistance increases， the separation scale changes little， the peak of the residence time becomes higher， the axial mixing effect is worse， the probability of the maximum shear stress greater than 10 kPa reaches 83%， and the degree of agglomeration of the dispersed phase decreases. The innovation is reflected in the use of finite element method instead of experimental process， which significantly reduces the measurement difficulties and human errors due to the complexity of the experiment， reduces its cost and cycle， and can play a guiding role in the actual production process.

Keywords： kenics static mixer; melt spinning; finite element method （FEM）; tracer particle technology; aspect ratio; inlet flow rate; max shear stress

收稿日期：20220513

網络出版日期：20220708

基金项目：浙江省重点研发计划项目（2022C01226）

作者简介：祝鑫（1999—），男，湖北荆州人，硕士研究生，主要从事聚合物材料加工数值模拟方面的研究。

通信作者：吕汪洋，E-mail：luwy@zstu.edu.cn