小数和分数不可混为一谈

唐启科

【摘 要】“数的认识”整理与复习，是对小学阶段所学“数的知识”进行整理归纳。对于小数和分数，有争议也有认识误区，本文从“分数的意义是什么？小数的意义是什么？小数是分数的另一种形式吗？”这三个问题出发，分析提升，得出：由于小学阶段没有学习除π以外的无理数，因此，学生认为分数和小数是一致的，但实际上学了无理数后，学生知道有限小数和无限循环小数能用分数表示，无限不循环小数，如π不能用分数表示。

【关键词】数的分类 小数 分数

一、缘起

每到六年级第二学期，数学教师就开始准备进行小学阶段总复习的备课了，复习的第一项内容就是“数的认识整理与复习”，这是对小学阶段所学“数的知识”进行系统的归纳整理，对中学学习也有一定的铺垫作用。通过系统整理复习，教师不仅要引导学生对数的认识和分类进行回顾，而且要引发学生新的思考。但每次进行集体备课时，教师们都有很多争议，也存在认识误区。争议主要集中在以下几方面：

1.小数是分数的另外一种表现形式吗？

2.数分为整数和分数两大类还是整数和小数两大类，或者分为整数、小数、分数三大类？

3.对于小数、分数意义的表述，相比较而言，学生对什么是分数理解得较好，但在复习阶段让学生说小数的意义，学生几乎难以表达清楚。

在复习阶段，教师应以什么方式让学生对数的意义有系统理解和归纳？很多教师匆忙中直接百度，并未对其中内容进行甄别就加以使用。如对数的分类，有些教师直接使用了思维导图（见图1）。

这个思维导图很容易给学生一种错觉：数分为整数、分数、小数三类。实际上我们提出数的分类时，很多学生都会脱口而出：数分为整数、分数、小数。

二、思考

在六年级毕业前，学生要对小学阶段知识进行整理复习，这是为接下来的中学学习做好知识储备。因此，在整理复习时，教师既要引导学生对小学阶段所学内容进行整体的复习，又要引导学生对中学数学内容有一个大致了解。笔者认为，要对小学阶段的“数”进行准确分类并让学生理解，首先要解决三个问题：

1.分数的意义是什么？

2.小数的意义是什么？

3.小数是分数的另一种形式吗？

三、分析

【教学片段1】

师：老师有4个苹果，平均分给两个小朋友，每个小朋友可以分多少个苹果？

生：4÷2=2，每个小朋友2个苹果。

师：如果老师有2个苹果，平均分给两个小朋友，每个小朋友可以分多少个苹果？

生：2÷2=1，每个小朋友1个苹果。

師：那如果老师只有1个苹果，要平均分给两个小朋友，每个小朋友可以分多少个苹果？

生：半个苹果。

师：你们能用喜欢的方式表示半个吗？

生1：我画了一个苹果，把它从中间分开。

师：你画得可真形象，是个小画家，这样表示一半特别直观。

生2：我就写了一个字——半。

师：你写这个“半”字，一竖下来就能体现出从中间分开。

生1：我用1/2表示。

师：同学们可真有办法，用自己喜欢的方法表示一半，不过，一半更科学的表示方法就是用表示，你们知道这是什么数吗？

生：分数。

分数的意义是什么？教材中这样描述：把单位“1”平均分成若干份，表示这样一份或几份的数，叫作分数。大部分数学教材在安排分数的意义教学时，都安排了“分数的初步认识”“分数的再认识”两部分内容，学生对“一个物体或者一个图形的几分之一、几分之几”的意义是理解的，建立了比较准确的表象，但对“一些物体或一些图形的几分之一、几分之几”的意义理解并不深刻。对于为什么要学习分数，教材交代得不是很清楚。分数与除法、比的关系，北师大版数学教材针对这一内容做了几次修订。其实学完这些内容后，很多学生对于这几种关系仍然难以理解。张奠宙先生认为：把除法和分数的模型简单化，对于解释数学教学的本质是有害的，除法有“等分除”和“包含除”之分，分数有“量的意义”和“率的意义”之分，教师和学生都要明白。的确，分数的出现是人类文明史上具有里程碑意义的一件事，从多角度来研究分数的教学也是一个值得研究的课题。也就是说，目前学生对于分数概念的建构，基本是建立在“分苹果”等简单模型上，理解得并不是很深入。

小数的意义是什么？这个问题如果在六年级的复习课上提出，几乎没有学生能回答出来。学生四年级时学习了小数意义，但对这个概念的理解还是比较浅的。对于小数的意义，教材是这样描述的：把单位“1”平均分成10份、100份、1000份……这样的1份或几份是十分之几，百分之几，千分之几……像这样的分数可以用小数表示。北师大版数学教材从人民币的元、角、分来引进小数，然后引导学生将抽象的数“1”进行十等分，主要通过数的改写来认识小数。小数和整数在形式上是统一的，小数的出现也使得十进制计数法从整数扩展到分数，数的内涵更加丰富了。数的表现形式改变了，但其中不变的是相邻两个计数单位之间的进率还是10。

小数是分数的另一种形式吗？其实小数并不是将分数改写而成的，而是自然数的十进位值计数规则进行扩展的结果，0.1是1/10的一种新的表述方法，但是为什么要将1/10写为0.1呢？实际上，这是为了与自然数的写法匹配。针对小数的教学，一些教材是先讲一部分分数内容，再讲小数，便于学生更好地理解小数的意义。北师大版数学教材先讲分数再讲小数，讲小数时不强求概念的严密准确，而是结合学生的生活经验采用描述性定义的方法讲小数，符合小学生的认知规律。因为在小学阶段学生没有学习无理数，所以在有理数的范畴内分数和小数是一致的，因此教师并不能简单地告诉学生小数是分数的另一种形式。

那么在小学阶段，数应该怎么分类呢？

【教学片段2】

师：在小学阶段，我们学过哪些数？谁来说一说？

生1：我们学过整数、分数、小数、自然数、负数。

师：还有吗？

生2：正数、0、百分数、奇数、合数。

师：你们能用思维导图把小学阶段学过的数进行整理吗？

生3：我们小组通过整理，把数分为整数、小数、分数三类。

师：与这一小组同学想法一样的同学请举手。（占了班级半数以上）还有其他想法吗？

生4：我们小组把数分为正数、0、负数三类。

生5：我们小组把数分为整数、分数……

生6：我们小组把数分为整数、小数……

师：请大家看老师整理的思维导图（出示教材思维导图），你们有什么想法？

生7：我发现，数分为整数和分数，但是小數为什么没有出现？

师：你这个问题提得真好，大家请看，我把小数添加在分数里了。在小学阶段，因为我们没有学习除π以外的无理数，所以我们认为分数和小数是一致的，因此在图中用“分数（小数）”表示（见图2）。

数学新课标指出，整体把握教学内容，在小学阶段要重视对数与运算主题的整体理解，重视数的抽象性，通过打通不同数集之间的关联，体会计数的规律，感受十进制数的意义，把握整数、小数和分数的一致性。在数的认识结构上，教师应该整体把握数集内部的一致性和数集间的一致性，数内部的一致性即数的意义、表示方式、大小等，其核心是数的意义。整体把握不仅有助于深刻理解数的概念的本质，还能迁移到数的运算过程中。学生在感悟数的一致性过程中，学会用整体的、联系的、发展的眼光看问题，培养了科学精神和理性思维。

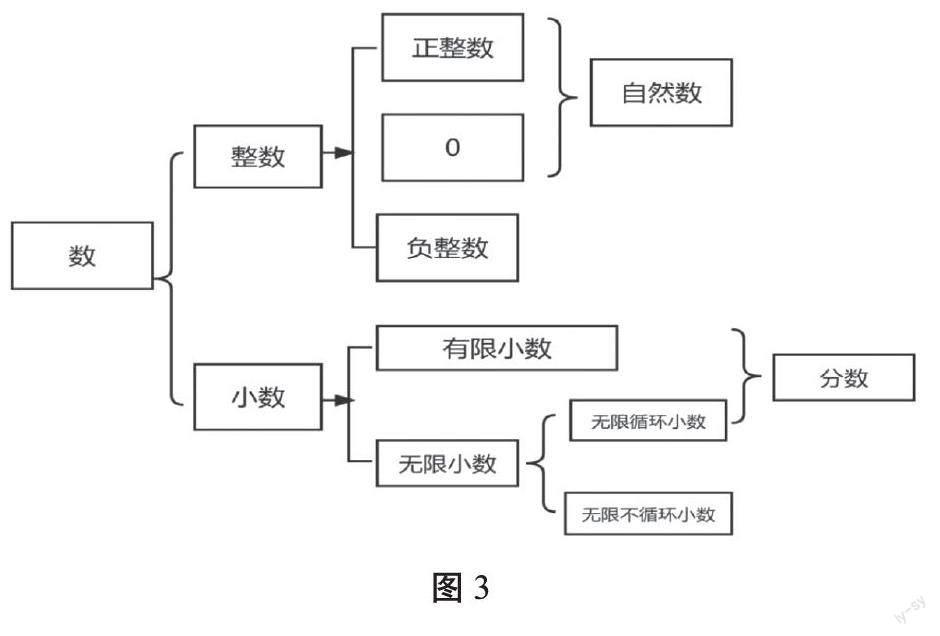
北师大版数学教材是按图2的思维导图进行整理的，将数分成整数和分数两个维度，强调在小学阶段因为学生没有学习除π以外的无理数，所以在有理数范畴内分数和小数是一致的，因此在图中用“分数（小数）”来表示。实际上分数和小数是有区别的，有限小数和无限循环小数能用分数表示，无限不循环小数，如π不能用分数表示，分数多是有理数，而小数中，有限小数和无限循环小数是有理数，无限不循环小数是无理数。那么还可以怎么分类呢？笔者在教学中出示了教材中的思维导图，并结合接下来七年级学习的实际情况，给学生整理出了思维导图（见图3）：

【教学片段3】

师：同学们，你们很快就将步入中学学习，老师根据中学数学内容，给大家整理出了思维导图，你们有什么想法？

生1：为什么要将分数括在有限小数和无限循环小数后？

生2：不能直接把有限小数、无限小数括在一起吗？

师：为什么要将分数括在有限小数和无限循环小数后，而分数又不包括无限不循环小数？这个问题你们到了中学后就能明白了，老师期待到时候同学们能想起老师的这种分法，并进行解释。

教师应让学生带着问题去探究，带着问题进入下一阶段的学习，学会用整体的、发展的眼光去探究问题，这样学生才能获得全面的发展。