引水隧洞围岩参数反演模型及蠕变特性研究
李 涛
(甘肃水利机械化工程有限责任公司,甘肃 兰州 730000)
0 引言
我国地形情况负载复杂,水资源分布严重不均,导致我国水资源调配工作很受地形条件的限制[1-2]。为解决水资源调配过程中的效率问题,引水隧洞工程是实现水资源运输的有效方式。地下通道能跨越多种地形环境实现直线资源运输,并排除地形障碍物对资源调配的负面影响[3-4]。但是引水隧洞工程往往处于地下较深处,深埋隧洞的施工难度和复杂程度较高,建设风险相对较大[5-6],且隧洞岩体挤压和衬砌作用力等因素也可能导致隧道结构稳定性降低,出现蠕变变形等问题[7-8]。因此,为探究引水隧洞围岩的参数特性,该文利用多智能学习算法构建引水隧洞参数反演组合模型,为维护引水隧洞工程的稳定提供助力。
1 引水隧洞围岩参数反演及蠕变特性分析
1.1 引水隧洞围岩参数反演组合模型设计
软岩是岩土工程中的常见岩体类型之一,软岩具有流变性强、地应力偏高等特点,在具体施工环境中容易引发隧洞衬砌变形等多种问题。随着我国对地下水资源的进一步开发利用,引水隧洞的利用率也逐渐攀升,引水隧洞修建围岩的环境条件也各有不同。部分引水隧洞在软弱围岩环境下修建,对引水隧洞围岩环境参数进行反演分析能为引水隧洞的修建提供技术支撑,对提升引水隧洞安全性和稳定性具有重要价值。因此,该文针对引水隧洞围岩参数反演问题,以引水隧洞围岩弹性模量、黏聚力、泊松比和内摩擦角指标为切入点,提出了基于多种机器学习算法的参数反演组合模型,组合模型运行框架如图1 所示。
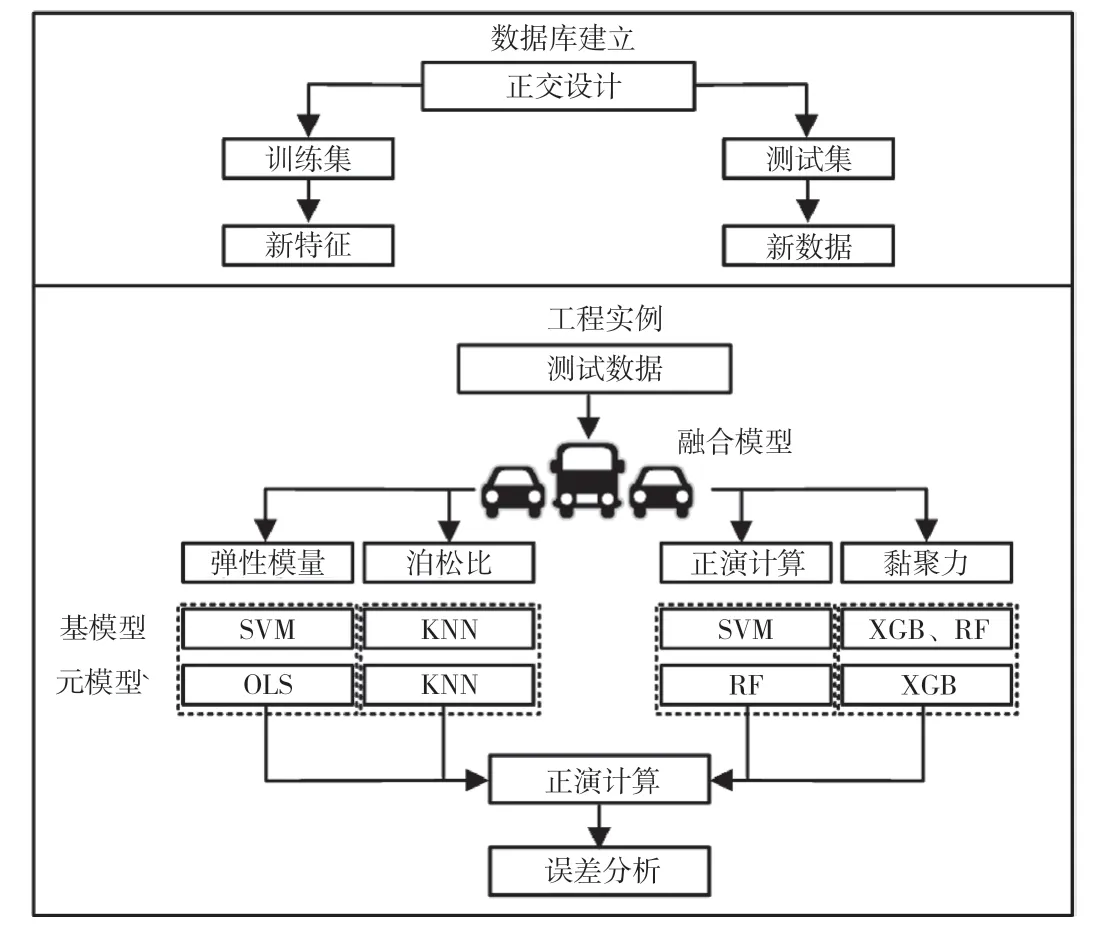
图1 参数反演组合模型运行框架
该文将支持向量机(Support Vector Machine,SVM)、最小二乘法(Ordinary Least Squares,OLS)、k-近邻算法、随机森林(Random Forest,RF)以及XGBoost 算法作为组合模型的基础算法,为4 个围岩参数反演提供不同的算法组合,并通过数值模拟和正交试验相结合的方式建立模型数据集。组合模型函数如公式(1)所示。
式中:A(x)和B(x)分别为最小二乘法函数和XGBoost 函数;b为回归因子;xi和yi为数据属性;ω为权重;l为损失函数;θ为叶节点分数;λ为正则化参数;γ为节点分裂评价参数;i为数据数量,i=1,2,…,n;C(x)为随机森林预测函数;Ti(x)为预测值;D(x)为支持向量机回归公式;ai和ai*为拉格朗日乘子;H(xi,x)为核函数;e为惩罚系数;E(x)为k-近邻算法距离求解函数,X和Y为数据矩阵;d为欧氏距离。
1.2 引水隧洞蠕变分析
岩石蠕变是岩土工程中的常见现象,软岩环境下蠕变变形的出现概率相对较大。受到高地应力的影响,硬岩地层工程完成后仍然会出现一定蠕变现象,严重的蠕变变形可能会引发倾倒坍塌等重大工程灾害。为了对引水隧洞蠕变特性做进一步分析,该文使用FLAC 3D 软件进行引水隧洞的三维数字模拟计算,通过有限差分的方式对引水隧洞围岩性态进行模拟分析。在有限差分模拟分析过程中,根据平衡动量方程对有限差分网格节点进行模拟,结合高斯定律获取围岩应变率,构建岩体应力应变关系的本构模型,然后结合围岩物质特性和本构关系对岩体应力特征进行分析。
根据Burgers 模型进行分析,FLAC 3D 软件计算过程中的自定义时间步长最大值函数如公式(2)所示。
式中:σK和ZK为Kelvin 体的黏性和剪切模量;σM和ZM为Maxwell 体的黏性和剪切模量。
2 引水隧洞反演计算及蠕变特性分析
2.1 参数反演模型效果分析
该文以甘肃某引水隧洞为研究对象。该引水隧洞进口和出口底板高程分别为2955.6m和2917.8m,全长22.61km,是一种无压引水隧洞。在引水隧洞进口段采用TBM 开挖,开挖直径5930mm。该引水隧洞的围岩占比超过70%,自稳时间较短。采用FLAC 3D 搭建数值模型,应用实体单元来进行数值模拟,并对引水隧洞的拱顶、拱底以及左右拱腰进行位移监测,计算围岩参数对各个位置位移的影响,结果如图2 所示。

图2 围岩参数对各个位置位移的影响
图2(a)是弹性模量对各个位置位移变化的影响,可以看出随着弹性模量不断增加,拱顶、拱底以及左右拱腰的位移逐渐减少。图2(b)是泊松比对各个位置位移变化的影响,可以看出,当泊松比不断增加,拱顶、拱底以及左右拱腰4 个位置的位移值不断减少。图2(c)是内摩擦角对各个位置位移变化的影响,可以看出,内摩擦角的增加会导致拱顶、拱底以及左右拱腰的位移值减少。图2(d)是黏聚力对拱顶、拱底以及左右拱腰4 个位置位移量的影响结果,可以看出,黏聚力增加会导致各位置的位移减少。从以上结果可知,引水隧洞的围岩参数对各位置的位移具有显著影响,其中弹性模量对各位置唯一值的影响最大,泊松比的影响最小。
通过重复性试验来计算数值模拟结果,将计算得出的结果数据作为测试数据集,并将数据集中的80%设置为训练集,将剩余的20%设置为预测集。利用测试数据集来评价该文所选择的模型的预测效果,如果平均绝对误差(Mean Absolute Error,MAE)小于4 则满足精度要求。计算结果见表1。

表1 模型平均误差测试
在表1 中,该文共设置5 组试验来比较反演模型预测值与实际值之间的误差,评价反演模型的准确率。结果显示,反演模型在泊松比和黏聚力预测中的预测值与实际值之间的MAE 均小于0.5,其中泊松比的MAE 仅为0.06。在弹性模量与内摩擦角的预测中,该文提出的反演模型的预测MAE 分别为1.3 和1.7。以上结果表明,该文所提出的反演模型能够在围岩参数预测中表现出较高的精度,能够满足基本的精度要求。最后,为进一步验证反演模型的有效性,设置2 组8 个监测点进行反演计算,并比较反演结果与正演结果的误差,结果见表2。

表2 反演验证结果
从表2 可以看出,在2 组8 个监测点的反演结果中,以监测点的实测值为输入值,第一组中反演得到的弹性模量、泊松比、内摩擦角以及黏聚力参数结果分别为14.4GPa、0.32、34°、1.5MPa。将第一组的反演结果作为输入,计算得出监测点的正演值。对正演结果与实测结果之间的误差进行分析可知,第一组的计算相对误差最大仅为4.46%。在第二组试验中,反演得到的弹性模量、泊松比、内摩擦角以及黏聚力参数结果分别为13.8GPa、0.35、32.5°、1.5MPa。利用反演结果来进行正演计算,得到的正演结果与实测值的最大相对误差仅为4.56%。以上结果表明,该文提出的组合参数反演模型计算结果与实际值之间的相对误差较小,即组合参数反演模型在围岩参数反演中具有较高的准确度。
2.2 蠕变特性分析验证
采用FLAC3D 建立蠕变特性分析模型,以六面体网格来进行模型计算。在模型建立过程中,设置围岩蠕变参数,包括剪切模量和黏性模量。为探究引水隧洞的蠕变特性,对围岩蠕变位移进行分析,结果如图3 所示。

图3 围岩长期蠕变位移分析
图3 中模拟了引水隧洞洞顶、洞底的竖向位移和洞腰位置的水平位移累计100 年后的变化。由图3 可以看出,在长时间的累积变化中,引水隧洞的洞顶、洞底的竖向位移和洞腰位置的水平位移最大值分别为9.13mm、6.94mm、8.03mm。可以看出,最大值出现在断层内。原因是断层围岩的蠕变特性更强,断层内的围岩蠕变会影响外部围岩,导致掌子面刚进入断层时,断层内的软弱围岩就对外部围岩产生了较强的蠕变影响。不同位置的位移量存在差异的主要原因是洞顶最先接触断层,而洞底最后接触断层,因此其掌子面进入断层后的位移变化存在差异。最后,分析引水隧洞洞顶、洞底以及洞腰不同时间的位移变化,并分析引水隧洞蠕变规律,如图4 所示。

图4 引水隧洞蠕变规律
从图4 可以看出,引水隧洞洞顶、洞底以及洞腰的位移变化在前40 年的蠕变变形速率较大,在40~50 年时蠕变变形速率开始缓慢下降。50 年后,引水隧洞洞顶、洞底以及洞腰的位移稳定上升,即此时处于稳定蠕变阶段。
3 结论
为了研究引水隧洞围岩的参数特性,该文根据SVM、OLS 等多智能学习算法构建了引水隧洞参数反演组合模型,并以弹性模量等指标为切入点进行反演分析。研究结果表明,泊松比和黏聚力预测MAE 为0.06 和0.4,弹性模量与内摩擦角预测MAE 分别为1.3 和1.7,4 个指标的反演预测MAE 值均小于2。与正演结果相比,参数反演结果的最大相对误差为4.56%,证明模型参数反演精准度较高。目前,该文利用组合算法进行参数反演分析,今后还需要对智能学习算法进行进一步改进,以提高模型组合性能,并提升参数反演效果。

