面向水坝变形与应力监测的混合模型构建研究

朱全海

（甘肃水利机械化工程有限责任公司，甘肃 兰州 730000）

0 引言

水坝在使用过程中会受外力、自身结构及周围环境等因素的影响，如果发生意外，可能会产生较大的经济损失，因此保障水坝的安全是水坝建设的重中之重[1-2]，这也是在水坝正常运行期，需要对坝体进行变形、渗流和应力应变等方面进行监测的原因[3]。对观测数据进行分析和构建观测模型，可以更好地认识坝体的安全状态及发展趋势[4]。该文为解决对大坝监测数据分析中存在的精度不足问题，将传统的统计学监测模型与有限元分析技术结合起来构建预测水坝应力应变的混合模型，并对大坝的运行状态进行预测，以尽早发现数据异常，预防重大事故或灾害发生。

1 水坝应力应变监测混合模型

1.1 水坝应变监测混合模型

该文尝试综合使用有限元技术与统计学方法构建混合监测模型，提高监测模型的监测性能。混合模型中使用有限元技术计算水压分量，其他分量采用统计学方法计算。该文对选中的研究对象以每周一次的频率观测数据，大坝坝顶水平位移会受温度分量、时效分量和水位分量等影响，该文选取坝顶水平变形最大的位置进行建模分析。

混合模型中的水压分量按照物理学中的水压理论计算，考虑实例中布置的温度计数量极少，无法测量出实际的温度场，因此选择多周期谐波计算温度因子项比较合适。时效分量数据较完整，采用统计学方式获取。根据研究实例的设计院资料，项目中的混凝土与基岩的弹性模量、泊松比、容重分别取28500MPa、0.167、2500kg/m3与35000MPa、0.3、2600kg/m3。为了兼顾多种上、下游水位情况，下游水位以平均值34m 为准进行计算，上游选择8 种水位，分别是40m、41m、42m、43m、44m、45m、46m 以及49m，其中40m、44m、46m、49m 分别代表最低水位、死水位、最高水位和校核洪水位。将选中位置的坝顶断面作为研究对象，先对这一界面的细部尺寸进行简化。参考行业的计算经验，将地基深度设置为坝高的2 倍，上、下游方向长度取坝高的2.5 倍。边界条件设置如下：基岩上、下游被施加水平法向约束，基岩底部被施加竖直方向的约束，坝段纵向被施加水平约束。根据重力坝的受力和结构属性，测点所在坝段更适合采用平面的方式分析应变，这样能减少工作量并提高分析结果精度。经过多次尝试后确定将研究对象的二维平面单元划分为2712 个节点和2588 个单元最合适。根据设计出的有限元模型进行水压分析，计算结果见表1。

表1 各上游水位条件下的选定坝段水平位移模拟计算值

按照表1 数据与水位数据进行拟合计算，可得到选择位置的水压拟合回归方程，温度分量分别根据统计方法得到。根据得到的各变形分量构建水坝混合应变监测模型，再使用Python编程语言对测点位置进行回归分析，以优化混合模型，优后结果见表2。根据表2 可知，混合模型的F检验对应P值都小于0.01，可认为模型的回归方程是显著的。各分量的T检验对应P值也小于0.01，说明回归系数显著性良好，且复测定系数R2=0.885，与0.9 较接近，表示模型的拟合效果良好。

表2 基于Python 语言的混合模型回归结果

根据表2 的计算结果，可得到混合模型的回归方程，如公式（1）所示。

式中：t为监测时刻，单位为d；δ（t）为混合模型中监测时刻t的总应变，单位为mm；H为监测位置相对地基表面的高程，单位为m。

1.2 水坝应力监测混合模型

最终将研究对象的二维平面单元划分为2694 个节点和2488个单元最合适。对选定截面位置使用Python编程语言进行回归分析，以优化混合模型，优后结果见表3。根据表3 可知，混合模型的F检验对应P值小于0.01，可以认为水坝应力监测混合模型的回归方程是显著的，不需要做进一步调整。各分量的T检验对应P值也小于0.05，说明回归系数显著性良好。应力混合模型的复测定系数R2=0.945，高于0.9，表示模型的拟合效果非常好。而水压细分量的调整系数为1.518，存在一定较小的偏差，也进一步说明了混合模型的设计前提假设较合理。应力混合模型的回归系数绝对值偏大，说明温度变化对水利工程应力的影响也较大。具体来看，由于季节因素，选定大坝位置的温度也呈周期性变化规律，从而使对应的应力数据也呈周期性变化规律。时效因子在前期的变化相对更大，但随着时间的增加，时效因子变得越来越稳定，没有明显的局部暴增、暴减现象。应力数值类型为压应力，这也和重力坝的实际表现情况一致。

表3 基于Python 语言的混合模型回归结果

根据表3 的计算结果，可得到混合模型的回归方程，如公式（2）所示。

2 混合模型监测成果分析

2.1 水坝应变监测混合模型分析

该文选取甘肃地区某水利枢纽工程为研究对象，为对比模型的计算性能，将混合模型计算结果和实测资料、单一的统计模型计算结果进行对比。

首先，对比混合模型在水坝实例应变监测中的数据，如图1 所示。根据图1 可知，在训练数据对比中，混合模型的应变拟合数据与实测应变数据的差异较小，且变化趋势基本一致。在测试时间段内，混合模型回归数据与实测数据的平均绝对误差为0.57mm，绝对误差最大值为0.79mm，出现在2020 年11月30 日。而在预测时间段内，混合模型整体回归数据与实测数据的平均绝对误差为0.31mm，绝对误差最大值为0.57mm，出现在2022 年3 月22 日。

图1 混合模型计算应变与实测值的对比结果

其次，对比纯统计模型的水坝应变结果与实测值，如图2所示。图2 中使用的纯统计模型的F检验对应P值小于0.01，可认为回归方程显著。复测定系数为0.882，接近0.9，可认为方程的拟合效果良好。且自变量的T检验对应P值都小于0.01，可认为各自变量对形变因变量的影响都是显著的。根据图2 可知，纯统计模型在回归测试期间的应变数据与实测数据的平均绝对误差为0.68mm，绝对误差最大值为1.74mm，出现在2020 年12 月22 日。

图2 纯统计模型计算应变与实测值的对比结果

2.2 水坝应力监测混合模型分析

该节分析混合模型与纯统计模型对水坝应力的监测计算效果。

首先，分析混合模型在水坝实例应力监测中的数据，如图3 所示。根据图3 可知，在训练数据对比中，混合模型的应力拟合数据与实测应力数据相当接近，且变化趋势基本一致。在测试时间段内，混合模型回归数据与实测数据应力平均绝对误差为0.21MPa，绝对误差最大值为0.46MPa，出现在2021 年2 月15 日。而在预测时间段内，混合模型输出的应力预测值与实测值同样相当接近，混合模型整体回归数据与实测数据的应力平均绝对误差为0.17MPa，绝对误差最大值为0.29MPa，出现在2021 年4 月30 日。

图3 混合模型计算应力与实测值的对比结果

其次，对比纯统计模型的水坝应力结果与实测值，如图4 所示。图4 中使用的纯统计模型的F检验对应P值小于0.01，可认为回归方程显著。复测定系数为0.964，超过0.9，可认为方程的拟合效果良好。且自变量的T检验对应P值也全部小于0.01。分析图4 发现，纯统计模型在回归测试期间的应力数据与实测数据的平均绝对误差为0.60MPa，绝对误差最大值为0.86MPa，绝对误差最大值出现在2020 年10 月15 日。

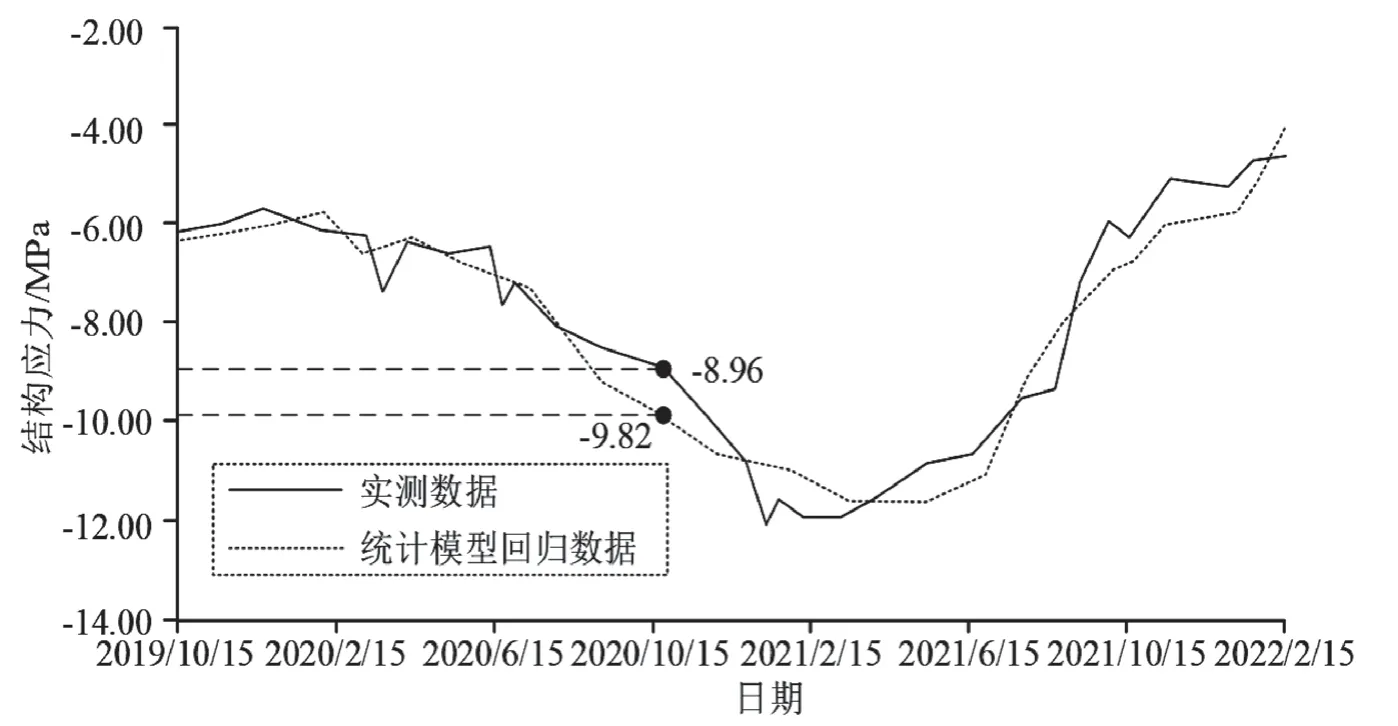
图4 纯统计模型计算应变与实测值的对比结果

3 结论

为准确地自动监测水坝的形变与应力，该文分别构建了纯统计学监测模型、混合统计学模型与有限元计算模型的混合模型。选取甘肃省某水利工程进行模型验证试验。试验结果显示，混合模型回归应变值与实测数据的平均绝对误差为0.57mm，绝对误差最大值为0.79mm，而纯统计模型的平均绝对误差为0.68mm，绝对误差最大值为1.74mm。混合模型回归应力值与实测数据的平均绝对误差为0.21MPa，绝对误差最大值为0.46MPa，而纯统计模型的平均绝对误差为0.60MPa，绝对误差最大值为0.86MPa。可见该文设计的混合模型具有更准确的监测效果，对保障水坝结构安全具有一定作用。