基于双向观测器的随机离散事件系统的不透明性
亓国照,刘富春,崔洪刚
(广东工业大学 计算机学院,广东 广州 510006)
离散事件系统是由离散事件按照一定的运行规则相互作用而导致状态演化的一类动态系统,在军事国防、交通控制、计算机集成制造系统、电子通讯网络、机器人技术等领域都有成功应用[1-5]。近年来,离散事件系统的不透明性(opacity)研究引起了国内外众多学者的广泛关注。离散事件系统的不透明性在数字签名、信息认证、数据加密等信息安全机制中有着重要应用[6-9]。
文献[10-12]研究系统的不透明性验证,并提出了多种不同类型的不透明性。文献[10]使用监督控制的方法确保系统不透明性。文献[13]中K步不透明性首先被提出。K步不透明性用来验证入侵者能否确定系统在特定时刻之后的K个状态是否存在秘密状态。文献[14]提出,当K趋于无穷时,K步不透明度变为无穷步不透明度。文献[14]提出了一种改进的方法,使用了一种称为双向观测器的结构。文献[15]在随机离散事件系统中研究无穷步不透明性和K步不透明性,并提出随机无穷步不透明性和随机K步不透明性。
本文继续文献[14-15]的工作,将文献[14]提出的双向观测器引入至随机离散事件系统,提出一种基于双向观测器的随机无穷步不透明性和随机K步不透明性验证方法。首先对随机无穷步不透明性和随机K步不透明性进行形式化定义。然后运用文献[15]中的方法,构造 (G,p) 的反向自动机GR,进而得到(G,p)的 双向观测器。通过(G,p)的双向观测器得到含有秘密状态的映射集,再以 (G,p)含有秘密状态的映射集构建验证器,得到一个基于双向观测器验证系统随机无穷步不透明性和随机K步不透明性的充分必要条件。最后提出一个基于双向观测器的随机无穷步不透明性和随机K步不透明性验证算法。
1 系统模型
经典离散事件系统表示为式(1)的不确定自动机[1]
式中:X为状态集,Σ 为事件集,δ :X×Σ →2X是状态转移函数,X0⊆X为初始状态集。用Σ∗表 示Σ 中元素的所有有限长度字符串的集合,包括空串 ϵ。语句L⊆Σ∗是有限长度字符串Σ∗的 子集。通常,Σ可划分为两个集合:可观测事件集合Σobs和不可观测事件集合Σuo。并且Σobs∩Σuo=ϕ∧Σobs∪Σuo=Σ。自然映射P:Σ∗→Σo∗bs可以递归定义为:P(ts)=P(t)P(s),t∈Σ,s∈Σ∗。当t∈Σobs时,P(t)=t;当t∈Σuo∪{ϵ} 时,P(t)=ϵ。
而随机离散事件系统[2]是在经典离散事件系统的基础上附加一个概率结构,通常用一个随机有穷自动机 (G,p)表 示,其中G=(X,Σ,δ,X0)是一个经典离散事件系统,p:X×Σ →[0,1]是概率转移函数。特别地,用p(σ|x) 来表示事件σ 在状态x发生的概率,它满足:(1) ∀x∈X:Σσ∈Σp(σ|x)=1 ;(2)∀x∈X,∀σ ∈Σ:p(σ|x)>0 ⇔δ(x,σ)!。
给定状态集q∈2X,用U R(q) 来表示可从q中的某个状态不可观测地到达的状态集,即
用N ext(q,σ)表 示当可观测事件σ ∈Σobs发生时可以立即达到的状态集,即
假设 α ∈P(L(G))是 一个可观测映射。用X︿G(α)表示映射α 发生时的当前状态估计,其定义为
当执行 β ≤α (即β 为α的前缀集合) 时,定义在已知可观映射α 的条件下β 的延迟状态估计为

给定r1,r2∈2X×X为两个状态对集合。操作◦:2X×X×2X×X→2X×X,其定义为
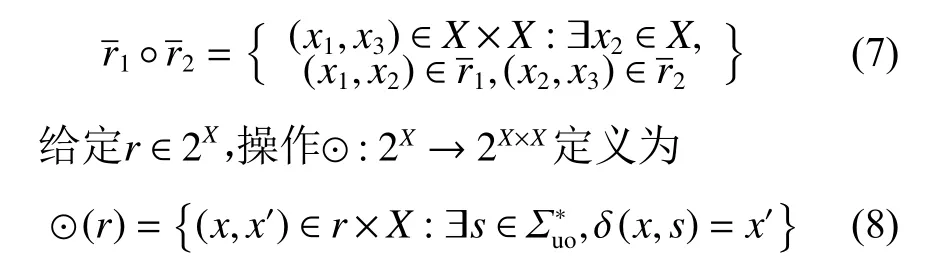
2 随机K步不透明性和随机无穷步不透明性
在实际应用中违反无穷步(或K步)不透明性的概率极其微小则可以忽略不计。定量评价无穷步(或K步)不透明性,还需考虑系统转移的概率。因此提出随机无穷步(或K步)不透明性定义。
定义1 给定一个随机离散事件系统(G,p)和秘密状态集为Xs及 阈值θ <1。记
如果Σs∈LPIFpr(s)<θ,则称(G,p)具有随机无穷步不透明性。
定义2 给定一个随机离散事件系统(G,p)和秘密状态集为Xs及 阈值θ <1。记
如果Σs∈LPKS pr(s)<θ ,则称(G,p)具有随机K步不透明性。
3 验证随机无穷步不透明性
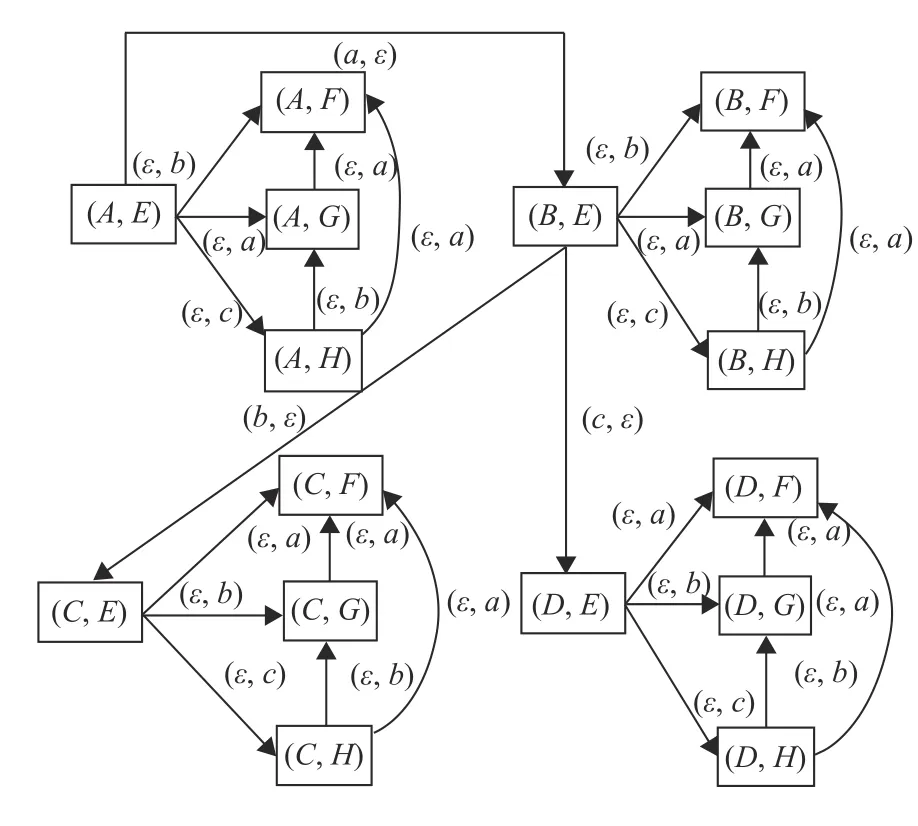
基于双向观测器 O bstw(G)[14]验证随机无穷步不透明性。
定理1 给定一个随机离散事件系统 (G,p),可观事件集为Σo,秘密状态集为Xs。给定Obstw(G)=(Qtw,Σtw,ftw,qtw,0)为 (G,p)的双向观测器,记
随机离散事件系统 (G,p)具有无穷步不透明性,当且仅当LIFS=ϕ。
证明 (充分性)设 ∃ (q1,q2)∈qtw,使q1∩q2≠ϕ并且q1∩q2⊆Xs。设s∈L(G) ,则∃t∈L(Obstw(G))使 得P(s)=τ1(t)(τ2(t))R[14]。已 知q1=fobs(x0,τ1(t))和q2=fobs,R(X,τ2(t)),那么

从而
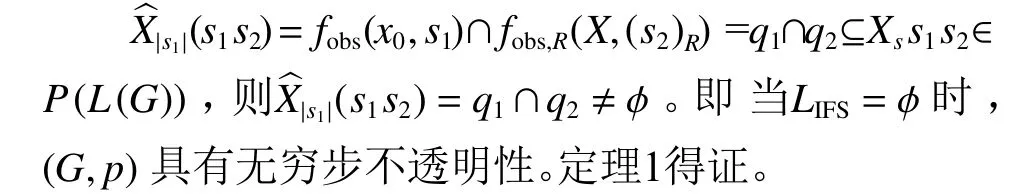
通过LIFS构建验证器VG[15]。记
对于任何ρ ∈2X×X,定义
作为 ρ的第一个分量中的状态集。对于任何R∈22X×X,定义
确定是否∃s∈LIF,就要确定QIF={(x,R)∈Q:∃ρ ∈Rs.t.l1(ρ)⊆Xs}是否为空。记
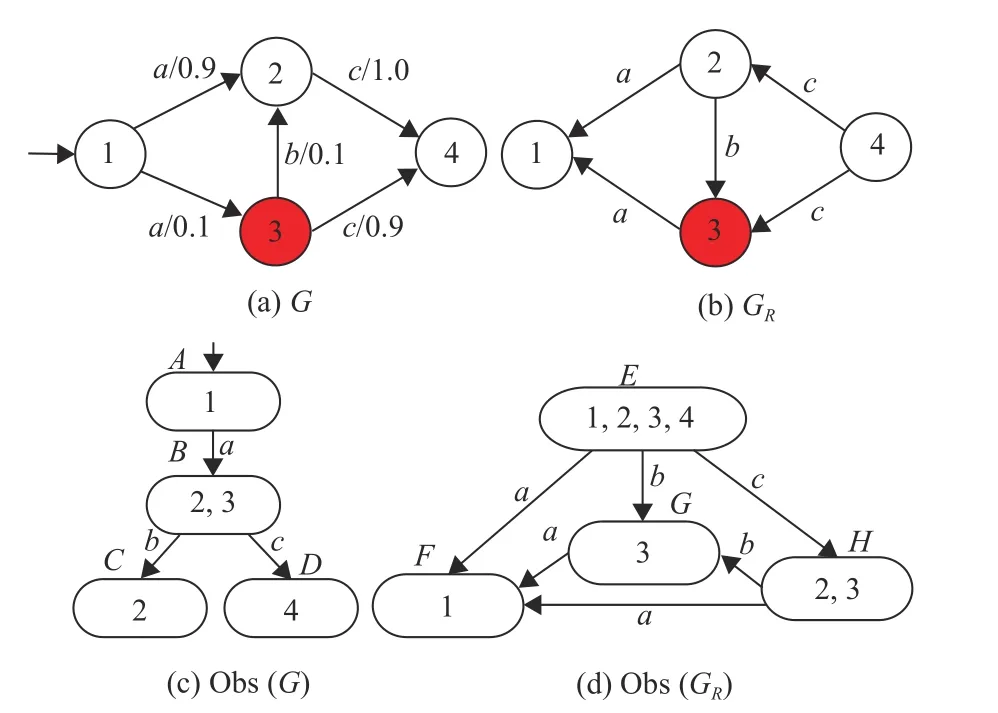
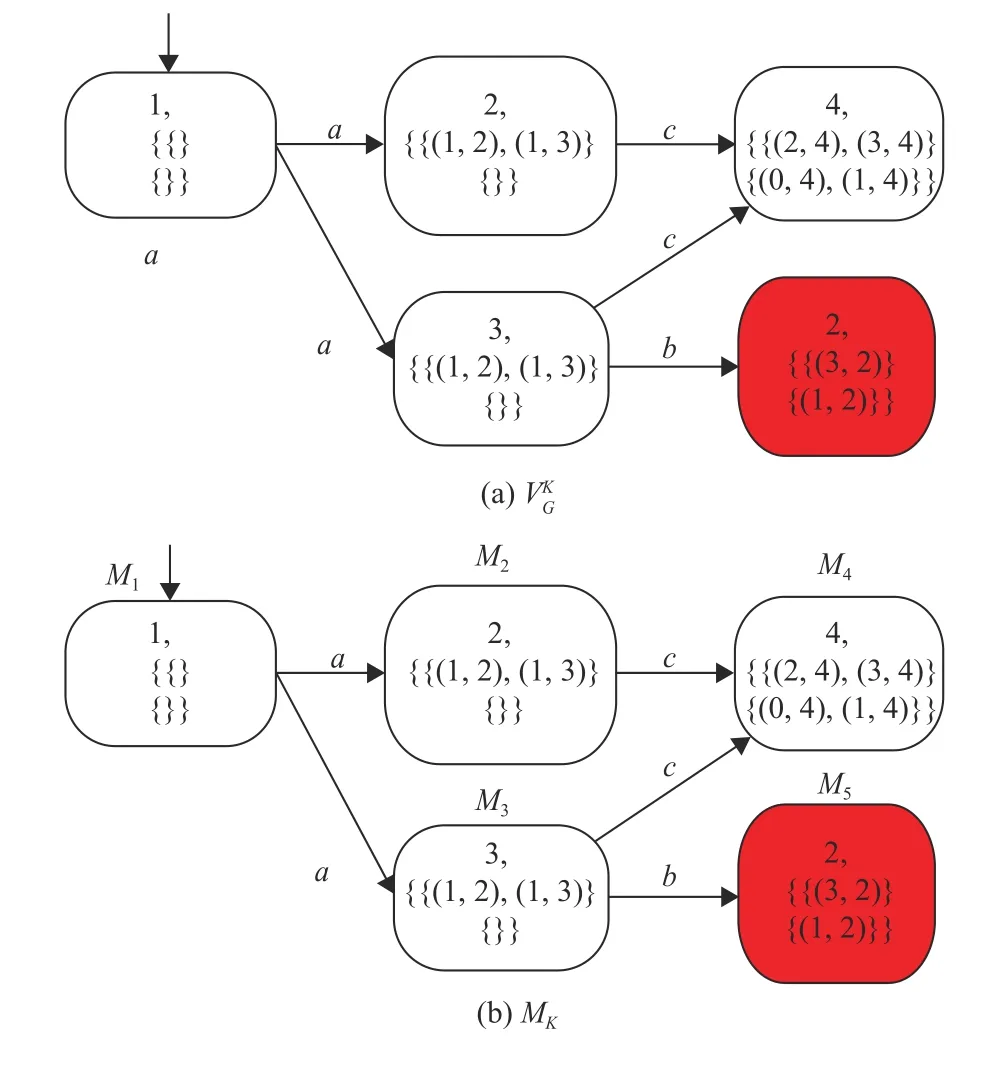
LIPF={s∈LIFS:[f(q0,s)∈QIF]∧[∀t 计算Σs∈LLPFp(s) ,首先定义VG=(Q,Σ,f,q0)[15]。然后定义马尔可夫链(MC)M=(Q,pM,π0),其中M状态空间与VG状态空间相同,转移概率函数pM:Q×Q→[0,1] 其定义为:对于任意q=(x,R),q′=(x′,R′)∈Q, 基于双向观测器 Obstw(G)[14]验证随机K步不透明性。 如果随机离散事件系统(G,p)具有随机K步不透明性,当且仅当LKS S=ϕ。 证明 (充分性)设 (G,p)具有K步不透明性,则∃(q1,q2)∈qtw,使q1∩q2≠ϕ且q1∩q2⊆Xs。 另有 则 (G,p) 具有无穷步不透明性当且仅当q1∩q2≠ϕ∧q1∩q2⊆Xs,|τ2(t)|>K[14]。即(G,p)具有K步不透明性时,LKS S=ϕ。 ( 必 要 性) 设LKS S≠ϕ ,则X︿|s1|(s1s2)⊆Xs。∃t∈L(Obstw(G)) 使 得q1∩q2≠ϕ ,并 且P(s)=τ1(t)(τ2(t))R,|τ2(t)|≤K[14]。则有 为了确定是否s∈,记 记: 在给定阈值θ 的情况下,检查 (G,p)是否具有随机无穷步不透明性和随机K步不透明性。基于上文的研究结果,提出以下算法。 算法1 输入:(G,p)=(Q,Σ,f,q0) ,可观事件集为Σo,秘密状态集为Xs,随机无穷步不透明性阈值θIF,正整数K,随机K步不透明性阈值θKS 例1 在访问服务器时,用户权限存在两种:超级用户权限和普通用户权限。用户在登入服务器后,首先要获取相应的权限。拥有超级用户权限或者普通账户权限的账号都可以访问服务器。服务器的账户系统非常严格,普通用户在做系统级别的更改时会受到用户权限的限制。用户登录服务器默认拥有普通用户权限。拥有超级用户权限的用户可以以普通用户的身份访问服务器,还可以执行普通用户无法进行的系统操作。同时,拥有超级用户权限的用户还可以授权其他用户为超级用户。超级用户权限为系统最高权限,不受安全系统限制。为防止入侵者获得超级用户权限,将“超级用户权限登入”看作是一个秘密状态。对于一个已设计的服务器系统,能否通过比较随机离散事件系统具有随机K步不透明性的阈值θ 与系统安全期望值,提前得到系统是否安全以便采取相应预防措施。 给定事件a为用户获取访问系统权限,事件b为超级用户权限转换成普通用户权限,事件c为访问系统。考虑如图1(a)所示用户访问服务器系统,其中状态1表示未登录用户,状态2表示用户以普通用户权限登入,状态3表示用户以超级用户权限登入,状态4为用户访问服务器系统。其中状态3被表示为秘密状态。当入侵者在入侵系统后可以确定用户是以超级用户权限登入(秘密状态)时,表明系统不具备随机K步不透明性。用字母A、B、C、D、E、F、H标识不同的状态集。将用户访问系统的事件看作随机离散事件系统的事件转移,投影为P:Σ∗→Σo∗,其中Σo={a,b,c},Xs={3}为秘密状态。 图1 系统G 其中的可观事件Σ obs={a,b,c} 和 秘密状态Xs={3}Fig.1 System G with Σ obs={a,b,c} 、Xs={3} 步骤1:求(G,p)的 O bstw(G),如图2所示。 图2 Obstw(G)Fig.2 Obstw(G) 步骤2:求得 (G,p)中含有秘密状态且满足K步不透明性的语言LKS S={ac,abc}。 图3 一个随机K 步不透明性的例子,其中K=1Fig.3 An example of almost K-step opacity, where K =1 由于P(M2)和P(M4)是一个自由项,所以上述方程的解不唯一。设P(M2)=P(M4)=0 ,而P(M5)=1,则P=[0.090 0.101] 。因 此π0(M1)×P(M1)=0.09。当系统安全期望值大于0.09时,此系统为随机1步不透明性。即入侵者无法在用户访问系统时确定用户是否是以超级用户权限登入。在设计这样的服务器时,可以通过算法1来判断所设计的系统是否安全。一旦所设计的系统不安全,则可以为保障拥有超级用户权限的用户不被发现而采取相应的控制手段(如提高普通用户权限使用频率、降低超级用户权限使用频率等),以规避超级用户权限被盗用的发生。 本文研究了基于状态的可观映射下随机离散事件系统是否具有随机无穷步不透明性和随机K步不透明性问题。将双向观测器引入随机离散事件系统不透明性研究,构造随机无穷步不透明性和随机K步不透明性的验证器,提出算法以验证系统是否具有随机无穷步不透明性和随机K步不透明性。

4 验证随机K步不透明性

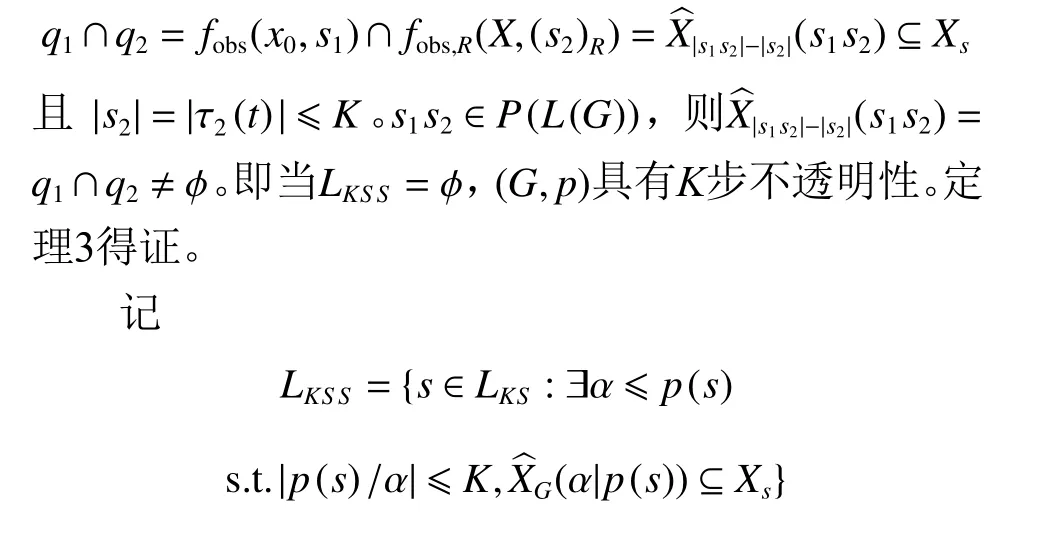


5 系统不透明性算法



6 结论

