地下工程岩体质量评判的三支决策方法

毛华,刘谦,连萌璇,王刚,张植明

(1.河北大学 数学与信息科学学院,河北 保定 071002;2.河北省机器学习与计算机智能重点实验室,河北 保定 071002;3.河北大学 生命科学学院,河北 保定 071002)

近年来,关于地下工程岩体质量给出了许多可行的科学性评判方法[1-5].对于地下工程岩体不同领域的研究也不断有新方法和新突破[6-9].这些方法都在所属领域有着优秀的指引作用,但是就广泛性而言,这些方法由于在决策时采用的是二支思维,导致存在一定的局限.

三支决策作为一种基于人类认知过程的决策方法[10-14],是通过“三分而治”思想,将人类解决问题时的思维模式进一步系统化,已成为人类处理不确定性问题代价较小的有效方法[15-22].计算机的思维方式和发展前提是已成功运用到许多领域[23-25]的人工智能信息的提取,而三支决策采用人类思维方式,现已成为信息处理和分析的有效工具之一.

1 地下工程岩体质量评判模型的建立

1.1 用模糊数学的方法对岩体进行排序

根据影响地下工程岩体质量因素的5个指标以及国家标准[26-27],设关于等级A的岩石质量最优指标为a1=RQD=95%、a2=RW=160 MPa、a3=KV=0.875、a4=Kf=0.9、a5=ω=5 L/(min·10 m),记{a1,a2,a3,a4,a5}为x.需要说明的是,在出水量定量描述中,一般以10 m洞长渗水量为统计量(单位为L/(min·10 m))代替原标准中单位渗水量。

定义1设论域U={x1,x2,…,xn}表示n个对象,其中每个xi为岩体样本,相应于国家标准中的5个指标,质量因素指标xi的实际取值记为{bi1,bi2,bi3,bi4,bi5}, 即xi={bi1,bi2,bi3,bi4,bi5}(i=1,2,…,n).

1)xi与国家标准x={a1,a2,a3,a4,a5}的接近程度定义为|xi-x|={|a1-bi1|,|a2-bi2|,…,|a5-bi5|}(i=1,2,…,n).

定义2设论域U={x1,x2,…,xn},xi与xj的二元比较级为(fj(xi),fi(xj)),称

(1)

为模糊相对比较函数.

定义3设论域U={x1,x2,…,xn},记rij=f(xi|xj),则称以rij为元素的矩阵R=(rij)n×n为模糊相及矩阵,于是,有

(2)

在模糊相及矩阵R中,对R的每行求下确界inf,以最大下确界所在行对应的xi为第1优越对象;划去第i行与第i列,得n-1阶模糊相及矩阵,类似地找出第2优越对象;此法一直做下去,就可对n个对象进行总体排序.具体算法过程如下:

算法1对岩体对象优越排序算法

输入:模糊相及矩阵R=(rij)n×n.

输出:岩体集合{x1,x2,…,xn}的最优排序{u1,u2,…,un}.

Step 1 对R的第i行求下确界

mi=inf{f(xi|x1),f(xi|x2),…,f(xi|xi-1),1,f(xi|xi+1),…,f(xi|xn)},(i=1,2,…,n).

Step 2 对Step 1中所得到的n个mi进行如下操作m=max{mi|i=1,…,n}, 由于n和mi的有限性,一定存在一个i0∈{i=1,…,n},满足mi0=m.

Step 3 对于第i0行中一定存在j0∈{i=1,…,m},使得f(xi0|xj0)=mi0=m.将f(xi0|xj0)记为第1优越对象u1.将第i0行和第j0列从R中划去,得到R的子矩阵,记为R(i,j).

Step 4 对R(i,j)重复上面的Step 1至Step 3,直至找到第n个优越对象un为止.

Step 5 输出{u1,u2,…,un}.

可以将上述过程综述如下:

首先,利用给定的岩体对象集,建立二元比较级.其次,利用算法1将得到岩体进行最优排序.

1.2 用贝叶斯最小风险准则对评判结果进行三分

设通过模糊相对比较函数对n个对象优越排序结果为U′={u1,u2,…,un},其中决策因素所组成的集合为V={v1,v2,…,vm}.

本文采用贝叶斯分类器,对得到的U′={u1,u2,…,un}进行分类,其分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类.

由于每个ui(i=1,2,…,n)均存在与国家工程岩体分级标准中的5个指标相应的数值,依次为bi1、bi2、bi3、bi4、bi5,由此,可以得到一个矩阵(bij)n×5.

具体操作过程如下,表1为文献[26-27]中的国家标准.

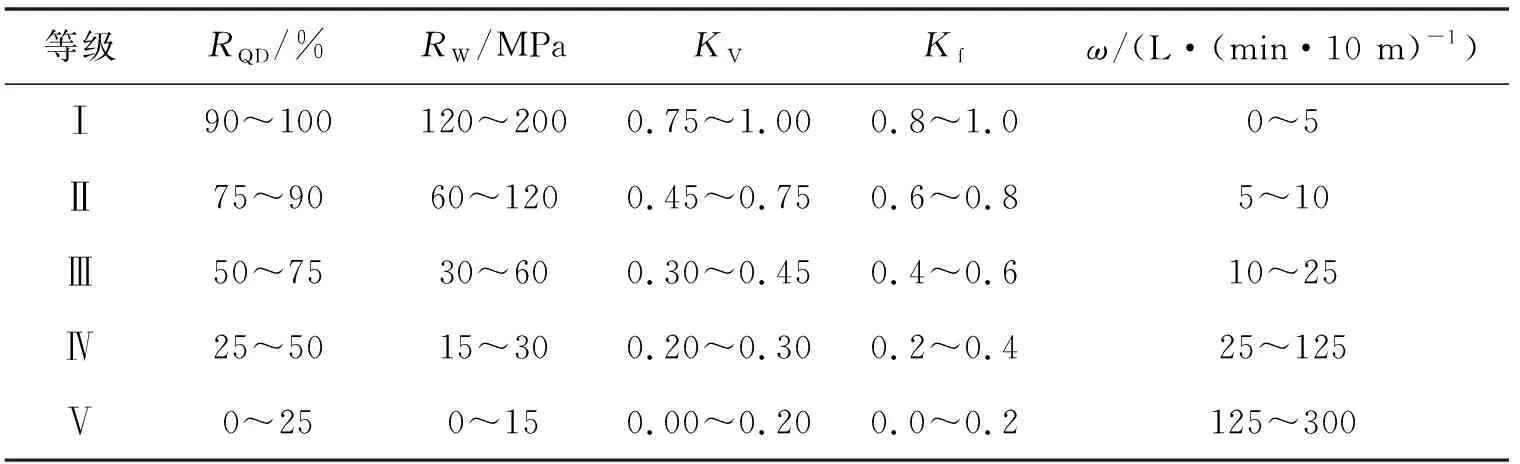
表1 地下工程岩体等级分类标准

将表1中的每个区间值取平均值得到决策表,见表2.

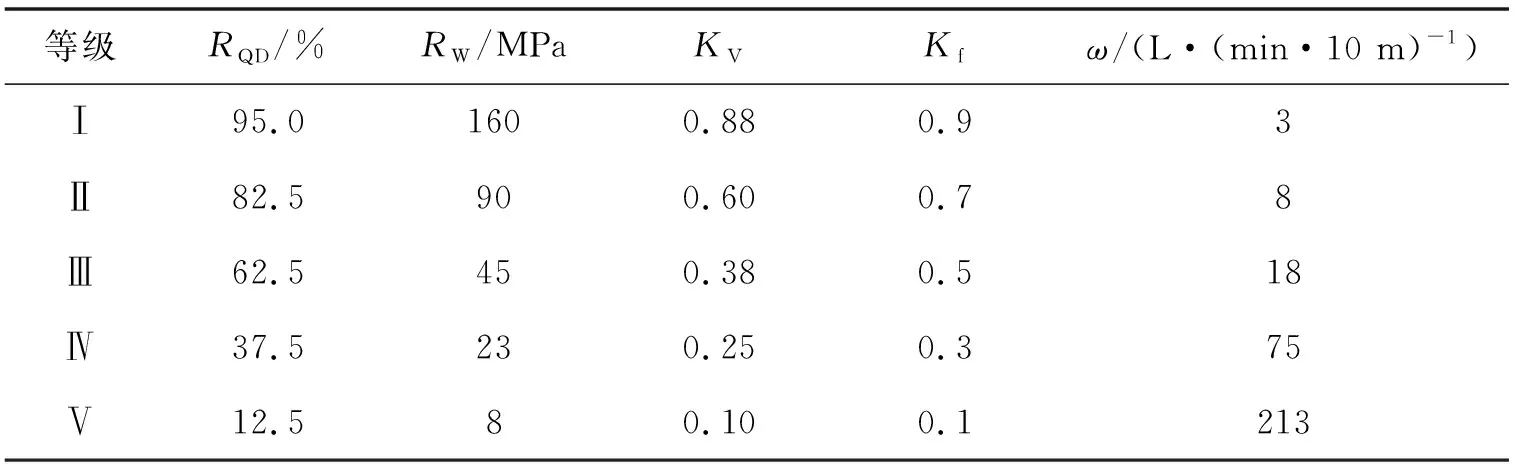
表2 决策表

将表2中的每个值记为ckj(k=1,…,5;j=1,…,5),得到如下矩阵:

(3)

将U′={u1,u2,…,un}中的任一个元ui={bk1,bk2,…,bk5},分别与R(ckj)5×5中的每一行相应的元,依据以下公式得到ui属于aj的概率(i=1,…,n;j=1,…,5).

(4)

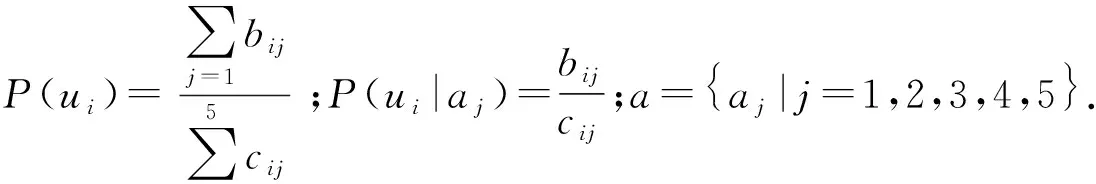
设做出正确判断的代价为0,即λPP=λNN=0,令λPP=3λBP,λPN=6λBN,λBN=2λBP,则

可以得到如下结果:

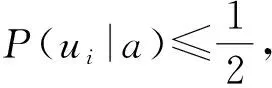
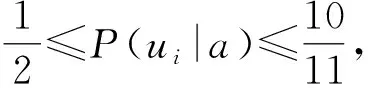
根据上述结果,可以对岩体质量的稳定性进行判断.

1)对于不稳定的岩体是不能转化为稳定的,直接建议用户不使用;

2)对于一般的岩体,可以通过分析P(ui|aj),P(ui|aj)的数据以及两者关系,找出造成岩体ui质量等级为一般的原因到底是哪个指标,再结合实际工程对不同指标的需求情况,给出是否对该工程可用岩体ui的决定.

3)对于稳定的岩体,可以直接提供给用户.

2 工程应用

例1用文献[2]中的数据,以某市抽水蓄能电站的工程岩体作为评判对象.该电站分2期建成,分别设1条引水隧道,用独立地下厂房和开关站.以2期3组真实数据为样本,见表3.

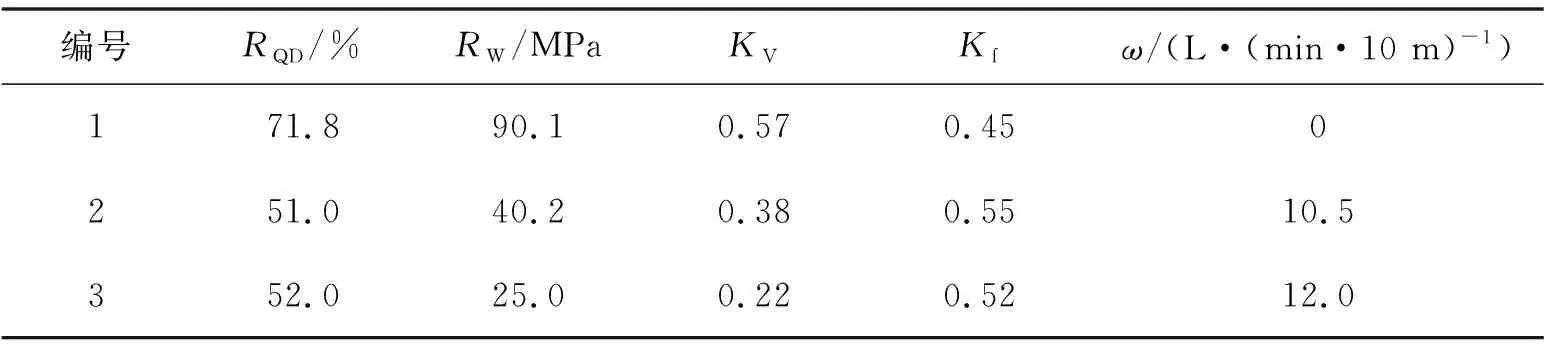
表3 地下工程岩体学习样本数据

下面将用本文的方法实现表3中地下工程岩体的质量评判.

设论域U={x1,x2,x3},其中xj为表3中的样本对象j(j=1,2,3).首先,通过算法1对3个地下工程岩体排序结果为{x1,x3,x2},得到新的排序.

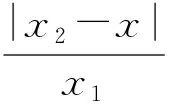
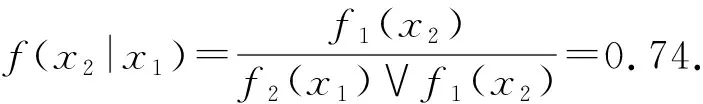
以此类推,可得论域U={x1,x2,x3}的模糊相及矩阵如下:

用算法1对R进行对象优越排序,结果如下表4.

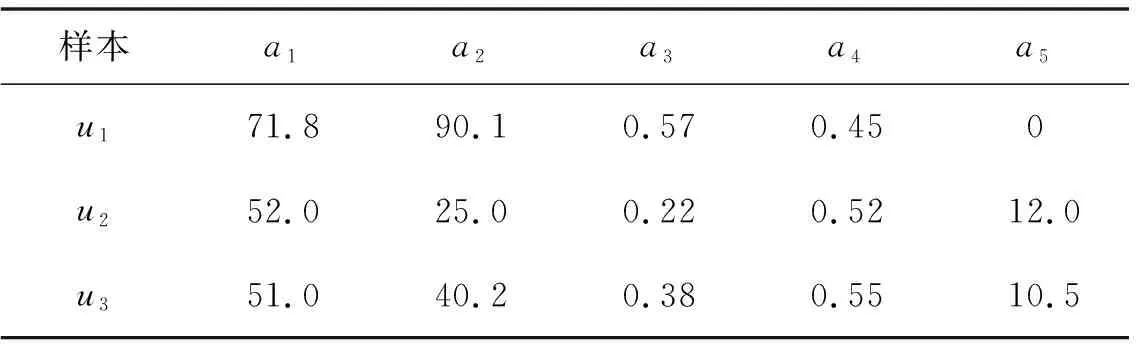
表4 用算法1对表3进行排序的结果

采用公式(4)分别计算岩体ui(i=1,2,3)属于等级Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的概率.

例如:计算u1属于等级Ⅰ的概率P(u1|a1)如下:

同样地可以算出u1属于其他等级的概率,以及其他2个样本分别属于等级Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的概率,其结果见表5.

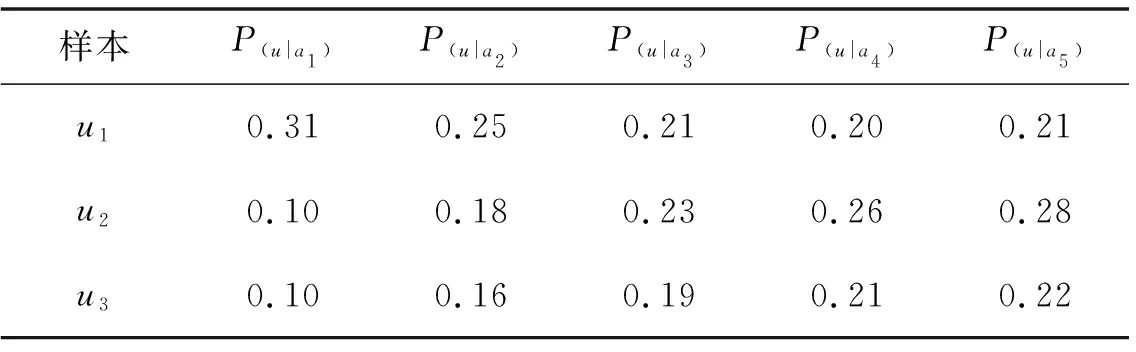
表5 岩体样本分别属于5个等级的概率

评判结果与文献[2]的评判结果相同.表明了本文给出的岩体质量评价的三支决策模型的有效性.本文中岩体质量评判指标有5个,虽然从数量上比文献[2]约简后的评判指标3个多2个,但是本文总体评判方法的复杂度为O(5n2)(由于每个对象岩体都需要考虑p个质量评判指标,本文中的p=5,所以本文总体评判方法的复杂度为O(pn2)=O(5n2)),远远小于文献[2]的O(25n).

表6为本文评判模型与文献[2]和文献[4]评判模型的比较.

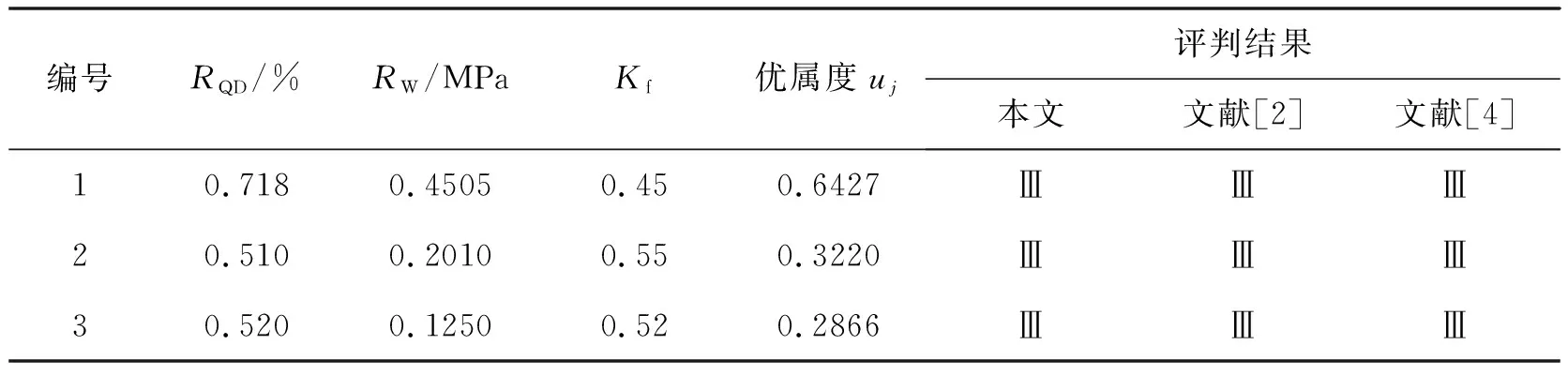
表6 某市抽水蓄能电站2期3组地下工程岩体质量评判结果

根据表6可以看出,本文三支决策评判模型与文献[2]和文献[4]评判结果相同,说明本文所给地下岩体的评判模型是有效的和可靠的.

本文方法与文献[2]和文献[4]的方法具体对比结果见表7.

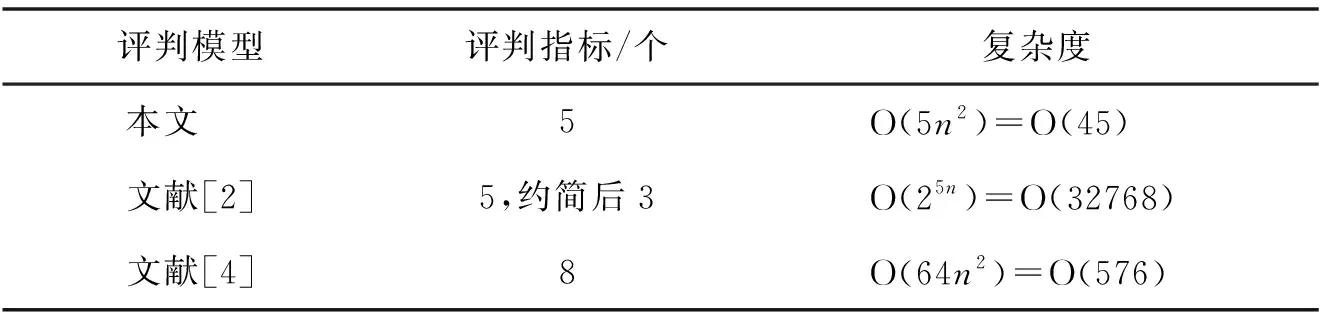
表7 本文与文献[2]和文献[4]方法数据对比结果

从表7可以看出45<576<32768,说明本文方法在复杂度方面远远优于文献[2]和文献[4]中的方法,即本文方法评判效率高.

3 结 语

本文通过三支决策的方法对地下工程岩体质量进行评判,根据贝叶斯准则对地下工程岩体样本进行三分:稳定、一般和不稳定.较国家标准工程岩体的5个等级而言,三分更加符合人类的思维模式.本文的算法过程也完全可以计算机化,算法针对对象不仅可以是地下工位岩体样品,还可以是其他对象,说明本文所建模型的方法适用范围, 除地下工程岩体外,还可以拓展到其他工程的质量评判中.