有趣的数阵图
朱 文
(江苏省常州市星辰实验学校)
小朋友,把一些数按一定的规则排成各种各样的图形,这种图形就是数阵图。填数阵图时,要仔细观察数阵图的结构,先填写关键位置(不同线的交点、封闭图形的顶点等)上的数,再通过尝试、调整,填出其他位置上的数。
例题1图1正中心圆圈内的数很特殊,每条线上都有它,我们把它叫作重叠数。你能将1~7按要求填在图1的圆圈内吗?
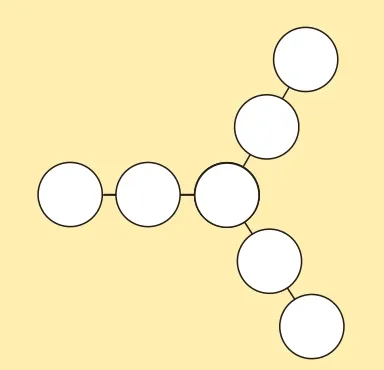
图1
(1)使每条线上3个数的和都是14;
(2)使每条线上3个数的和都相等。
(1)从图1中可以看出,在计算每条线上3 个数的和时,都要用到重叠数,确定重叠数是解题的突破口。
先算出所给7 个数的和是1+2+3+4+5+6+7=28,再思考重叠数是几。因为每条线上3 个数的和都是14,所以3 条线上各数之和是14×3=42,此时,重叠数被多加了2次,可求出重叠数是(42-28)÷2=7。
剩下的1,2,3,4,5,6,两两之和等于14-7=7 的有1 和6、2 和5、3 和4。图2是其中一种填法,通过调换数的位置(重叠数的位置不变),能得到多种填法。
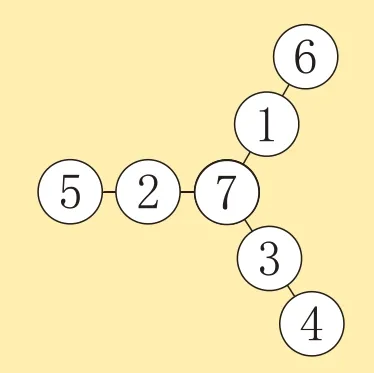
图2
(2)确定重叠数是解题的突破口。根据题意,在计算图1中3条线上的各数之和时,重叠数被多加了2次。若重叠数是a,要使每条线上各数的和相等,那么1+2+3+4+5+6+7+a+a(即28+2a)一定是3的倍数。因为a是1~7中的某一个数,逐个尝试可知,只有1,4,7符合要求。
当a=1时,每条线上的3个数之和是(28+1×2)÷3=10;
当a=4时,每条线上的3个数之和是(28+4×2)÷3=12;
当a=7时,每条线上的3个数之和是(28+7×2)÷3=14。
计算出了重叠数及相应的各条线上的数之和,再填数阵图就非常容易了,如图3、图4、图5所示,是3 种基本填法,通过调换基本填法中数的位置(重叠数的位置不变),能得到多种填法。
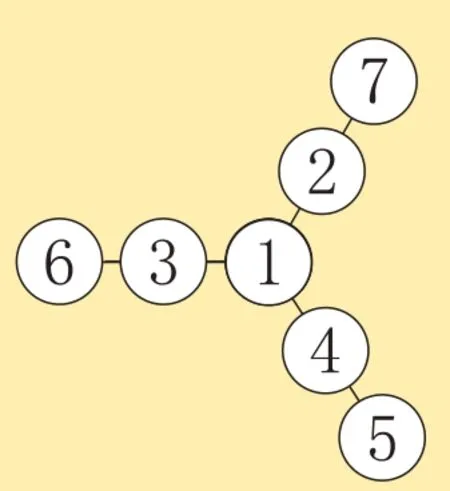
图3
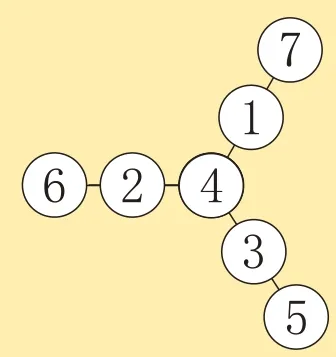
图4
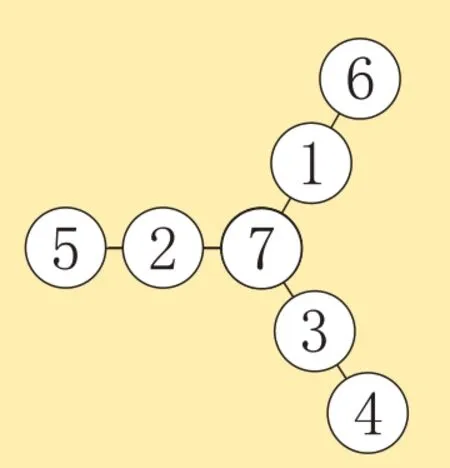
图5
像图1这样,从一个中心出发,向外作了一些线,这类的数阵图是辐射型数阵图。解题时常用的关系式:已知各数之和+重叠数×(线的条数-1)=一条线上各数之和×线的条数。
例题2图6中三角形3 个顶点处圆圈内的数很特殊,每个顶点处的数都在2 条线上,是重叠数。你能将1~6 按要求填入图6的圆圈内吗?
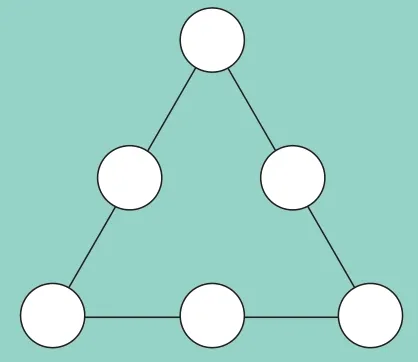
图6
(1)使每条线上3个数的和都等于9;
(2)使每条线上3个数的和都相等。
(1)从图6中可以看出,在计算每条线上3 个数的和时,都要用到重叠数,确定重叠数是解题的突破口。
先算出所给6 个数的和是1+2+3+4+5+6=21,再思考3个重叠数是几。因为每条线上3个数的和是9,所以3条线上各数之和是9×3=27,此时,3 个重叠数都被多加了1 次,可求出3 个重叠数的和是27-21=6。因为在1~6内,只有1+2+3=6,所以3个重叠数是1,2,3,再根据每条线上数的和是9,算出其他圆圈内的数,图7是其中一种填法,通过调换数的位置(3 个重叠数只能在3 个顶点处),能得到多种填法。
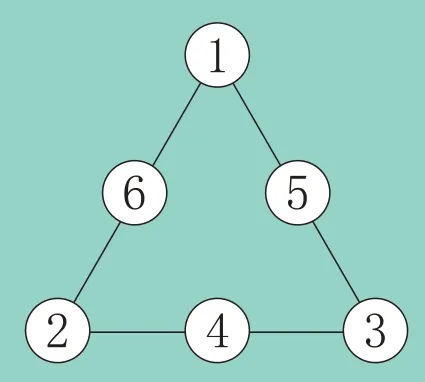
图7
(2)确定重叠数是解题的突破口。根据题意,在计算图6中3条线上的各数之和时,3个重叠数都被多加了1次。若3个重叠数是a、b、c,要使每条线上各数的和相等,那么3条线上的数之和1+2+3+4+5+6+a+b+c(即21+a+b+c)一定是3 的倍数。因为a、b、c分别是1~6中的某个数,逐个尝试可知:
当a+b+c=1+2+3=6时,3条线上各数的和是(21+6)÷3=9;
当a+b+c=1+2+6=1+3+5=2+3+4=9时,3条线上各数的和是(21+9)÷3=10;
当a+b+c=1+5+6=2+4+6=3+4+5=12时,3条线上各数的和是(21+12)÷3=11;
当a+b+c=4+5+6=15时,3条线上各数的和是(21+15)÷3=12。
即每条线上3 个数的和可以是9,10,11,12,对应的3 个重叠数的和分别是6,9,12,15。
经过尝试,只有当3 个重叠数分别是1,2,3;1,3,5;2,4,6;4,5,6时符合要求,这时每条线上3个数的和分别是9,10,11,12。
计算出了三角形顶点圆圈内的数及相应的各条线上的数之和,再填数阵图就非常容易了,如图8、图9、图10、图11 所示,是4 种基本填法。通过调换基本填法中数的位置(3个重叠数只能在3个顶点处),能得到多种填法。
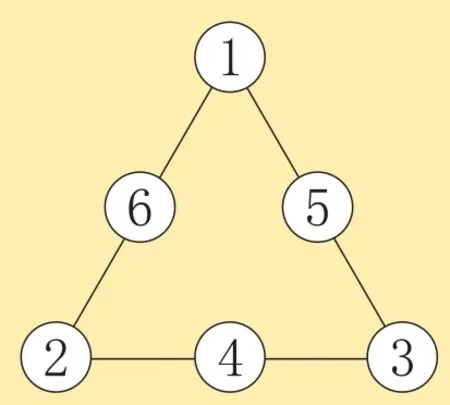
图8
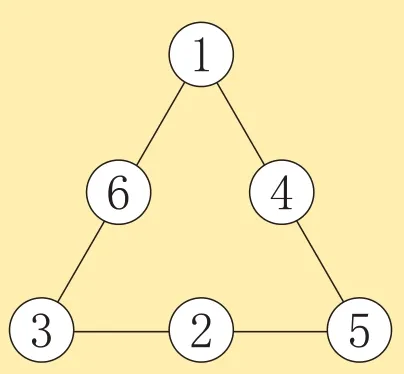
图9

图10
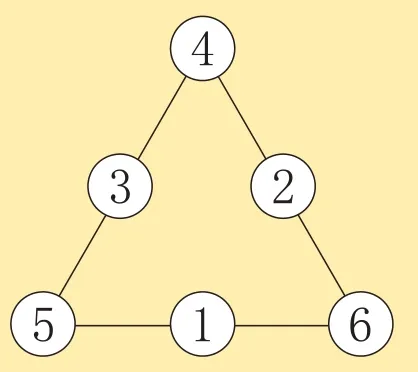
图11
像图6这样,各边之间相互连接,形成封闭的图形,这类的数阵图是封闭型数阵图。解题时常用的关系式:已知各数之和+重叠数之和=每边各数之和×边数。

