初中数学活动课跨学科融合的教学设计探索与实践

王晓娟

［摘  要］ 文章以“数学活动2”（杠杆原理）为例，谈如何进行跨学科融合教育——以杆秤平衡为背景，带领大家了解我国传统文化杆秤的历史发展，并通过收集、分析、验证数据等一系列实验活动，从数学的角度提炼出杆秤平衡中蕴含的数学关系，进而构建数学模型，让学生在实践活动中自然地实现数学与物理学科的融合.

［关键词］ 初中数学；活动课；学科融合；教学设计

引言及背景

《义务教育数学课程标准（2022年版）》（下稱《课程标准》）提出数学课程内容含数与代数、图形与几何、统计与概率、综合与实践四个学习领域［1］，而综合与实践旨在综合运用数学和其他学科的知识与方法解决问题，积累数学活动经验，发展核心素养. 教师应引导学生在数学活动课以问题和活动为载体，综合运用数学学科和其他学科的知识与方法解决问题，感受数学与其他学科的融合，体会数学的价值.

顾广林认为，数学活动课，顾名思义就是数学+活动，是指在教学过程中构建具有教育性、创造性、实践性的学生主题活动为主要形式，以激励学生主动参与、主动实践、主动思考、主动探索、主动创造为基本特征，以促进学生整体素质全面提高为目的的一种新型教学观和教学形式［2］. 一节精彩的数学活动课应该由一连串精心设计、动静结合、丰富多彩的活动组成，“学生因活动而主动，课堂因活动而扎实、高效和生机盎然”［3］.

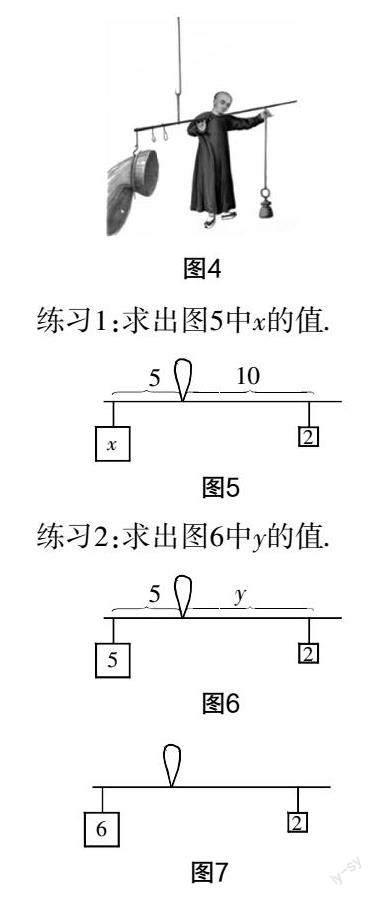
《课程标准》关注数学问题是否跨学科，这是数学教学改革中的新课题. 跨学科融合课程教学的核心意义在于，帮助学生建立知识之间的联系，以解决实际问题［4］. 在核心素养大背景下，重庆市九龙坡区教师进修学院举行了第二届“行知杯”优质课竞赛活动，笔者有幸参与并荣获区级一等奖. 笔者抽到的课题是人教版数学教材七年级上册第三章数学活动2. 这不是物理上的杠杆原理吗？学生通过实验记录并分析数据就能发现其中的规律，这有什么好讲的呢？但作为赛课，教学设计应推陈出新、独具一格，才能脱颖而出，获得佳绩. 笔者通过查阅大量的资料，与本组教师探讨商榷，发现我国的杆秤也力求质量平衡. 受此启发，笔者认为此课的教学设计可以浸润数学传统文化，促使学生积极地探索数学知识，并进行主动学习和探究. 于是，笔者将题目拟定为“一元一次方程的实际应用——杆秤平衡中的数学问题”. 现将这节课的教学设计片段和课后思考整理出来，与大家分享.

教学设计与实施

1. 教学目标的设计体现了跨学科教学的融合性

“杠杆原理”是跨学科整合课程活动之一，本活动从物理学具杠杆的认识入手，探索影响杠杆平衡的条件，其中引入“国粹”杆秤，将学科知识与技能、思想方法融合起来，能培养学生人文底蕴等核心素养，能让学生学会用数学眼光观察世界，用数学思维思考世界，用数学语言表达世界. 《课程标准》明确了活动2是动手试验与动脑分析相结合的内容，杠杆原理是基本的力学原理，学生通过简单试验就可以发现这个规律，于是这节课的教学目标可确定为：（1）学生通过实验探索和小组合作交流，分析数据，发现杆秤平衡的等量关系；（2）结合问题建立模型，进而用一元一次方程求杆秤平衡状态时的支点位置；（3）让学生得到充分动脑、动口和动手的机会，促使每一个学生自主学习，提高数学应用能力；（4）以杆秤发展的历史为背景，培养学生良好的数学思维品质，让他们充分感受学习数学的乐趣.

我们知道，学习物理等课程，推导公式时经常会采用类似的学习方法，因此，让学生以数学活动方式接触这节课，能为他们学习其他学科知识积累经验，这也是此数学活动课需达成的目标之一.

2. 教学内容的选择突出跨学科教学的整体性

“一元一次方程的实际应用——杆秤平衡中的数学问题”是笔者依据《课程标准》自主设计的课题，具体内容的设计不仅要新颖自然，还要突出跨学科教学整合的目的——巧妙地融入物理、传统文化等知识. 因此，进行教学设计时，笔者设定了如下教学内容.

（1）俗语知新——“导”

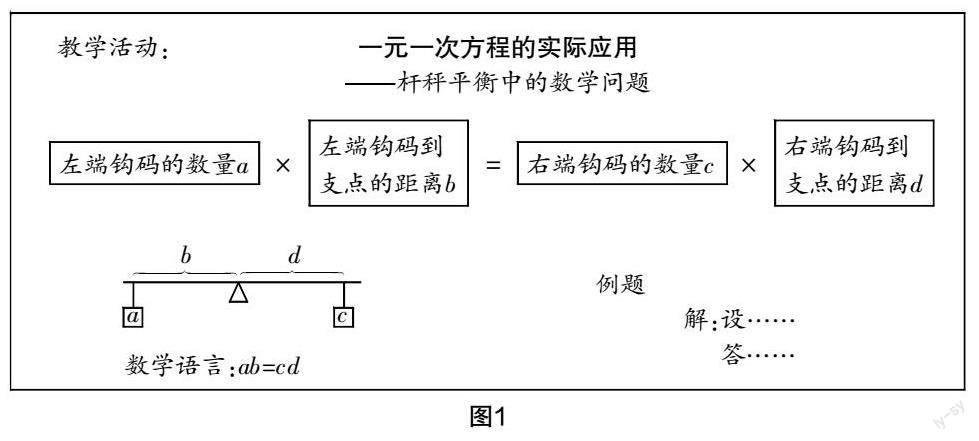
俗话说：“秤砣虽小压千斤. ”（引入课题）笔者让学生通过观看视频《天平秤》，达到介绍杠杆尺的目的，进而让学生感知水平方向上的“平衡”，并通过一步步引导，学生可以自行总结出影响平衡的4个因素，随即将影响因素用字母a，b，c，d表示. 板书设计如图1所示.

（4）总结升华——“评”

我们沿着杆秤发展的历史长河，通过观察、实验、收集数据、分析数据、验证数据，用合情推理的方法归纳出了杆秤平衡中的数量关系，在实验过程中经历了从特殊到一般的探索历程，体验了用一元一次方程解决实际问题的建模思想. 最后，请同学们通过观看视频《被数学选中的人》片段，体会数学的价值和意义. 此教学环节的板书如图8所示.

（5）作业——“再探”

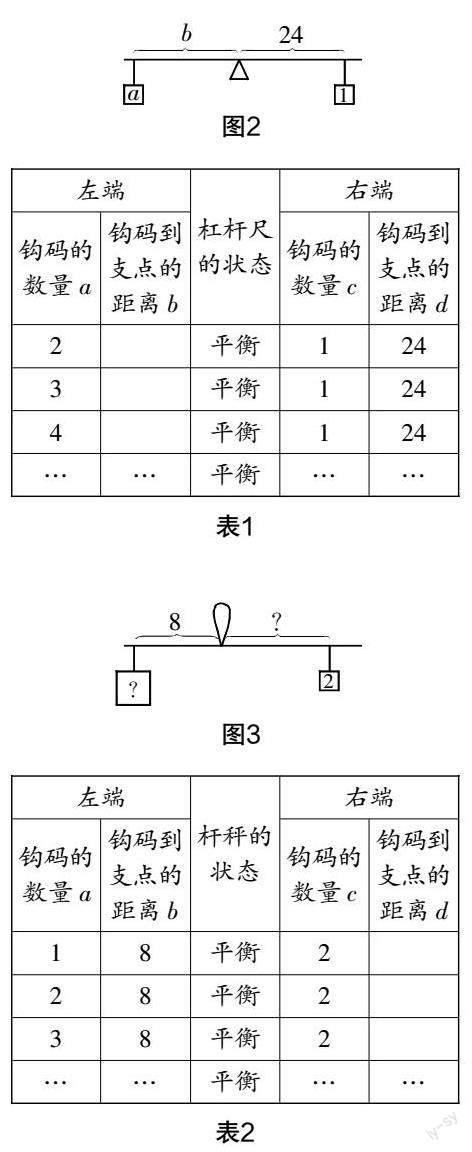
整个数学活动的探索实际上是进行了一个数量关系的推导，并让学生用实验的方法经历另一个数量关系的推导，这就为其他学科公式推导的学习奠定了坚实的基础.（比如图9）

3. 教法学法的实施强调跨学科教学的体验性

整个教学设计突出知识情境化. 杆秤经过了几千年的历史演变，我们研究它的时候，把它抽象成了数学模型，这样便于学生理解，如图10所示.

要达到良好的教学效果，教学设计的实施要注重教法学法. 跨学科整合课程的教学活动立足于学生的兴趣、需求，教师教学时要改变传统“教师教、学生学”的模式，增强知识与实际之间的联系，提高学生分析问题和解决问题的能力［5］. 实践式、互动式、体验式及小组合作等教学方法能激发学生的学习兴趣，能激活学生的思维. 弗赖登塔尔在长期的数学教学实践中总结出生活数学化和“再创造”理论，所以“数学活动课的目的之一就是让学生在活动中积累数学活动经验，经验是学生在动手操作和思维活动中获得的”［6］. 对于本课，在传统文化的背景下，学生置身于真实的学习环境去感受、去体会，从学习效果来看，既激发了学生的学习热情，又提高了学生的学习效率.

裴光亚先生概括出了数学教学的价值序列，即“知识、思想、基本能力、一般能力和更高层次的能力、人的发展和完善”［7］，这个序列可以看成课堂发展层层递进的一个顺序. 笔者正是用递进、深入的教学方式归纳整节课的逻辑顺序，学生的数学素养也在层层递进、潜移默化中渐渐养成. 这节课，学生既了解了中国传统文化知识，又亲身经历了平衡条件的探索历程，体会了数学建模思想，达到了《课程标准》提出的基本要求，经历了将知识学习过程转化为发展核心素养的过程.

几点启示

1. 找准学科知识的融合点

人教版七年级数学上册第三章的数学活动2，实际上是对杠杆平衡条件的探索和归纳. 要使杠杆保持平衡，需要满足“动力×动力臂=阻力×阻力臂”，这就是两个学科的“融合点”. 从物理学来看，它是杠杆原理；从数学来看，它是一个等式，而这个等式可以通过数学方法随意变形. 它们都指向同一个式子，所以只要教师在课程中牢牢把握“融合点”，不偏不倚，就能实现跨学科的恰当融合.

2. 立足本学科特色渗透互补，完成课堂实施的“融”

跨学科融合不是说把数学课讲成物理课，而是教学时要有数学学科特色. 众所周知，数学是其他学科的基础，是研究其他学科的有力工具. 比如物理中的很多公式和习题都需要借助数学知识来推导和演绎. 那么，在课堂教学过程中，就需要教师引导学生从数学的角度去看待杠杆原理的本质，用数学的方法去解决杠杆原理问题. 其实，很多时候物理中的方法和原理，也可以应用在数学当中. 所以，两者是相互渗透、互帮互助的，只不过教師在实施教学时要侧重本学科的特色.

3. 跨学科融合有助于培养学生的综合实践能力

《课程标准》的“综合与实践”领域明确提出，“能综合运用数学和其他学科的知识与方法”，感悟数学与其他学科的关联，发展学习能力、实践能力和创新意识. 事实上，任何一门学科的知识都不是孤立的，学科之间也不是毫无联系，它们就像一个知识系统上的各个分支，各学科之间有着千丝万缕的联系. 因此，教师在教学跨学科课题时，不仅要让学生在轻松愉悦的环境中不知不觉地达到教学目标，还要提升自身的综合素养.

结束语

本节课的教学设计推陈出新，恰到好处地实现了跨学科融合教学，达到了新、趣、活、实、美的效果. 教师引导学生用数学的眼光看待问题，用数学的方法解决问题，用数学的语言描述问题，诠释了让学生学会数学地思考世界的教育真谛！

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］顾广林. 初中数学活动课的实践与认识［J］. 数学教学通讯，2010（09）：25-27.

［3］董红锋. 活动，让数学课堂教学变得鲜活［J］. 河南教育（教师教育），2022（07）：61.

［4］张维. 基于核心素养的小学跨学科教学的课例研究——以小学英语学科教学为例［J］. 教育信息化论坛，2019，3（05）：248-249.

［5］谭梅，杨叶. 小学低段跨学科主题教学设计探究［J］. 教育与教学研究，2018，32（01）：95-100+127.

［6］吴开朗，朱茱，许梦日. 论汉斯·弗赖登塔尔的数学教育观［J］. 数学教育学报，1995（03）：17-21.

［7］裴光亚. 数学教学的价值序列［J］. 中学数学教学参考，2016（32）：1.