改进的ReliefF-BPNN分类模型

李雨沛 王新利

摘  要： 提出了一种改进的ReliefF-BPNN分类模型。该模型使用ReliefF算法和交互增益权重，来最大程度地保留相关特征与交互特征；同时在BP神经网络模型的误差函数中加入正则化项防止过拟合。实验表明，改进的ReliefF-BPNN在大多数数据集上的分类准确率高于90%，其精度相对于其他传统模型更高。

关键词： 特征选择； ReliefF算法； 交互增益； BP神經网络；分类

中图分类号：TP181          文献标识码：A     文章编号：1006-8228（2023）06-20-05

Improved ReliefF-BPNN classification model

Li Yupei， Wang Xinli

（College of Science， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： In this paper， an improved ReliefF-BPNN classification model is proposed. It uses the ReliefF algorithm and interaction gain weights to maximize the retention of correlation and interaction features. Meanwhile， a regularization term is added to the error function of BP neural network model to prevent overfitting. Experiments show that the classification accuracy of the improved ReliefF-BPNN is higher than 90% on most data sets， and its accuracy is higher than that of other traditional models.

Key words： feature selection; ReliefF algorithm; interaction gain; BP neural network; classification

0 引言

近年来，各种数据的爆发式增长，影响了数据的准确分类。面对高维的数据，特征选择是一个行之有效的方法。

特征选择有三种常用的方法，分别是包裹法、嵌入法、过滤法[1]。其中，过滤法评价准则简单、运算效率高，应用范围广[2]。ReliefF算法作为过滤法的一种，具有权重计算更简单且运行效率更高的优点，被广泛应用于特征选择[3]。另一方面，BP神经网络模型有诸多优点，如强自适应性，鲁棒性、非线性映射等，是一种使用面很广的分类模型，但是当模型的训练数据过少或数据存在噪声时会使分类模型产生过拟合现象[4]。许多研究者对BP神经网络的参数做出优化来避免这一现象[5]，例如将模拟退火算法和元启发式算法混合调整参数[6]、将自适应遗传算法应用于优化参数[7]等，但是应用不同的算法对BP神经网络进行优化往往计算复杂度高，实验难度大。

尽管ReliefF算法计算特征权重是根据特征在同类中的差异和特征在不同类中的差异来选择特征，合理考虑了特征与不同类别的相关性，但特征之间与类别还有一个不可忽视的关系，即特征的交互。一般来说，交互特征单独与类别无关，一旦将它们组合在一起，却又与类别很相关。保留交互特征是有利于分类的，而ReliefF算法忽视特征之间的交互，极大地影响特征选择的效果，进而影响分类。利用信息度量标准的互信息方法能够有效地度量特征之间的交互，许多特征选择算法是使用基于互信息的方法来度量特征的交互，最大程度地保留交互特征来优化特征选择的效果，进而提高分类准确率[8]。

本文在上述研究的基础上，提出了一种改进的ReliefF-BP神经网络分类模型。用ReliefF算法进行选择，选择出与类别相关大的特征，再使用标准化的交互增益权重，尽可能保留交互特征；然后采用加入[L1]正则化项的BP神经网络模型。与其他改进相比，该模型不仅结构简单，还能有效防止过拟合，提高分类的精度。与其他6种算法进行对比试验，结果表明，该模型的性能明显优于其他算法。

1 预备知识

1.1 ReliefF算法

ReliefF算法[9]的主要思想是，根据计算样本点的最近邻分布，计算特征权重值，选择出权重值较大的特征。从训练集[M]中随机选择样本[A]，再从和样本[A]同类的样本集中找到[k]个近邻样本，同时在每个与[A]不同类别的样本集中寻找[k]个近邻样本，然后根据以下规则更新权重：

[ωX=ωX-j=1kdiffX，Ai，Hjnk]

[+C≠ClassAPC1-PClassAi×j=1kdiffX，Ai，Mjnk] ⑴

其中，[ωX]表示特征[X]的权重，其初始值为0，[n]表示迭代次数；[Ai]表示第[i]次迭代随机选择样本；[k]表示选取的近邻个数；[Hj]表示样本[Ai]同类中的最近邻样本；[Mj]表示样本[Ai]不同类中的最近邻样本；[ClassAi]表示样本[Ai]所在的类别；[PC]表示第[C]类的先验概率；[diff（X，A1，A2）]表示样本[A1]和样本[A2]在特征X上的差别。

1.2 特征的交互

交互信息利用互信息来度量特征之间的交互，交互信息又称为交互增益（Interaction Gain， IG），指的是三方或者多方的交互作用，三方交互增益[10]的定义如下：

[IGfi;fj;C=Ifi，fj;C-Ifi;C-Ifj;C]  ⑵

其中，[Ifi，fj;C]表示特征[fi]和[fj]与类别C的联合互信息。当[IGfi;fj;C<0]或者[IGfi;fj;C=0]时，说明特征[fi]和[fj]提供了相似信息或者与类别无关；当[IGfi;fj;C>0]时，表示特征[fi]和[fj]组合提供的信息量大于特征[fi]和[fj]分别提供的信息量之和，说明特征[fi]与[fj]具有交互性。

1.3 BP神经网络模型

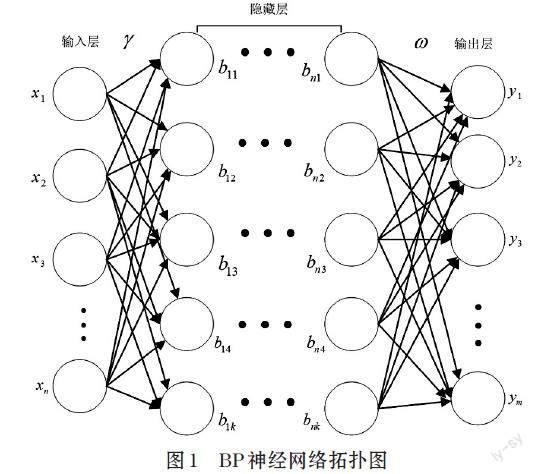
BP神经网络模型[11]的拓扑结构有三个层次，分别是输入层、隐藏层和输出层。输入层的节点由输入样本的特征个数决定，输出层的节点由分类结果决定。隐藏层的层数和节点一般由人工决定。BP神经网络模型结构如图1所示。

图1  BP神经网络拓扑图

其中，[x1，x2，…，xn]表示输入层神经元节点，即样本的特征；[y1，y2，…，ym]表示输出层神经元节点，即输出的标签；[b11，b12，…，b1k]表示第一层隐藏层的节点；[bn1，bn2，…，bnk]表示第n层隐藏层的节点；[γ]表示输入层节点到隐藏层节点的权值；[ω]表示隐藏层节点到输出层节点的权值。

2 改进的ReliefF-BPNN分类模型

2.1 基于特征交互的ReliefF算法

在⑵式的基础上引入标准化的交互增益来度量特征的交互。标准化的交互增益（Standardized Interaction Gain， SIG）定义如下：

[SIGfi;fj;C=IGfi;fj;CHfi+Hfj，SIGfi;fj;C∈0，1]  ⑶

在式⑴基础上，加入标准化后的交互增益权重，即为特征[Xi]的总权重公式为：

[ωXi=1Nj=1NSIGXi;Xj;C+ωXi]  ⑷

将式⑷作为权重更新的算法称为基于特征交互的ReliefF算法，即I-ReliefF算法，其步骤如算法1所示：

[算法1 I-ReliefF算法 输入：特征集[F=f1，f2，…，fn]，类别集[C=C1，C2，…Cm]，阈值[k]

输出：特征子集S

1. 初始化特征子集[S=?]；

2. Fori=0 to |F|

3. 根據公式⑶计算在所有F中特征之间的标准化交互增益权重

4. 根据公式⑴计算在所有F中特征的权重值

5. Endfor

6. For i=0 to |F|

7. 根据公式⑷计算保留特征的总权重值

8. Endfor

9. 对特征集S中保留的特征的总权重值进行降序排列，选择出系数值大的特征组成新的样本数据集 ]

2.2 加入正则化项的BP神经网络模型

在BP神经网络的误差函数计算公式中加入正则化项，改进后的误差函数为：

[E=1Ni=1NYi∧-Yi2+αω1]  ⑸

N表示训练样本的个数；[Yi∧]表示第i个样本的预测输出值；[Yi]表示第i个样本的实际输出值；[α]表示正则化系数；[ω]表示所有层向下层神经元传递时的权值组成的矩阵。

2.3 I-ReliefF-BPNN模型的建立

基于改进ReliefF-BP神经网络模型将简化后的数据分为70%训练样本和30%测试样本，训练样本应用于训练该模型，测试样本用于检验模型的分类精度。算法2描述了I-ReliefF-BPNN模型的基本步骤：

[算法2 I-ReliefF-BPNN模型算法 输入：数据集D，学习率[η]

输出：类别C，误差e

1.采用均值替代法对存在缺失值的数据集进行填补，接着做归一化处理。再对数据集使用I-ReliefF算法进行特征选择，将选择出的特征组成新的样本数据集。

2.创建网络

3.训练网络

Repeat for D

正向传播

反向传播

Until for 达到结束条件

4.使用网络

5.预测数据归一化 ]

3 实验

3.1 数据集与数据集的处理

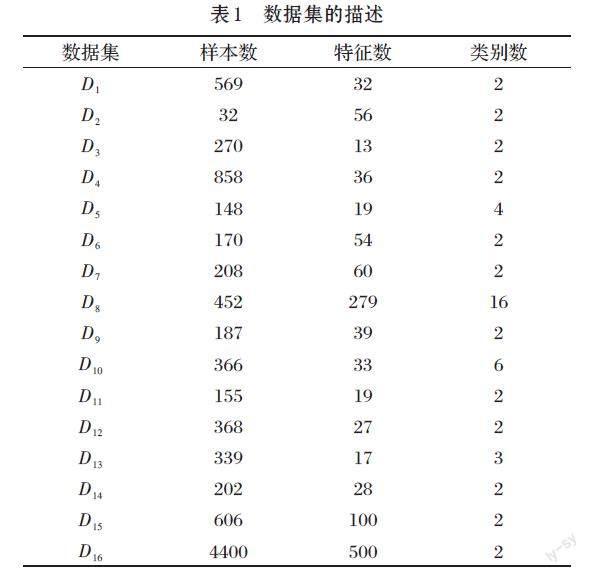
实验数据集：美国加州大学欧文分校提供的UCI数据库分别是[D1]（WDBC数据集）、[D2]（LungCancer数据集）、[D3]（HeartDisease数据集）、[D4]（Cervicalcancer数据集）、[D5]（Lymphography数据集）、[D6]（DivorcePredictors数据集）、[D7]（Sonar数据集）、[D8]（Arrhythmia 数据集）、[D9]（Bonemarrowtransplant：children数据集）、[D10]（Dermatology数据集）、[D11]（Hepatitis数据集）、[D12]（HorseColic数据集）、[D13]（PrimaryTumor数据集）、[D14]（RiskFactorprediction of Chronic Kidney Disease数据集）、[D15]（Hill-valley数据集）、[D16] （Madelon数据集）。表1介绍了16个数据集的样本个数、特征数和类别个数。

本文采用均值替代法对存在特征值缺失的数据集进行填补并做归一化处理；对于连续数据集，将连续数据集离散化。本文使用K-means算法进行聚类，k值根据类别个数确定，根据聚类的结果，将同一簇的记录并合并成一组中。

3.2 实验结果与分析

为了验证本文提出的模型的有效性，选取RF、SVM、BPNN、I-ReliefF-SVM、mRMR-BPNN、ReliefF-BPNN这6个分类模型与本文提出的I-ReliefF-BPNN模型进行对比。本实验中BP神经网络的迭代次数设置为1000，学习率设置为0.02，权值的初始化范围为-0.5到0.5之间。表2和表3表示16个数据集的分类准确率、[F1]指数。分类准确率和[F1]指数越高，分类效果越好。

如表2所示，本文提出的I-ReliefF-BPNN模型相较于6种分类模型的平均分类准确率在16组数据集上有明显提高。注意到BPNN的分类准确率相较于SVM和RF分别平均高6.25%、4.24%，表明BPNN相较于传统分类器分类精度更高；I-ReliefF-BPNN与mRMR-BPNN、ReliefF-BPNN相比，准确率分别平均高5.83%和3.48%，表明本文提出的I-ReliefF算法相比于其他特征选择算法，更有利于BP神经网络的分类。

如表3所示，本文提出的I-ReliefF-BPNN模型在16组数据集上[F1]指数较BPNN平均高0.0544，较ReliefF-BPNN平均高0.0673，较mRMR-BPNN平均高0.0911，较I-ReliefF-SVM平均高0.1078，较SVM平均高0.1206，较RF平均高0.1128，说明本文提出的模型在分类上更具优势。

4 结论与展望

本文提出了一种改进的ReliefF-BP神经网络模型，即I-ReliefF-BPNN模型。考虑到医疗诊断数据集中，许多诊断指标之间存在交互，选取关于医疗诊断方面的数据集进行实验验证。从16组数据集的实验结果来看，该模型中的I-ReliefF算法与传统的特征选择方法相比，从后续的分类中可看出此算法有效提高了分类的准确率；模型中改進的BP神经网络分类模型与其他同类型的分类方法相比，分类精度明显提高，两者结合其分类能力相比于其他分类模型在分类准确率，[F1]指数更高。

但是，I-ReliefF-BPNN模型存在一些不足之处，主要有以下两点：①I-ReliefF-BPNN模型运行时间相较于BP神经网络模型更长；②本文提出的模型在某些不平衡数据集上[F1]指数不高，分类效果并不理想。因此，未来仍需进一步优化搜索算法，缩短整个算法的运行时间；针对不平衡数据集，考虑将不平衡数据处理方法加入本模型中，提高不平衡数据集上的分类效果。

参考文献（References）：

[1] Dia S， Guilermo， Cortes L， et al. A review of algorithms to

computing irreducible testors applied to feature selection[J]. Artificial Intelligence Review，2022

[2] 李郅琴，杜建强，聂斌，等.特征选择方法综述[J].计算机工程

与应用，2019，55（24）：10-19

[3] Song Y ，Si W Y， Dai F F ， et al .Weighted reliefF with

threshold constraints of feature selection forimbalanced data classification[J]. Concurrency and computation： practice and experience，2020，32（14）

[4] 沈波，谢兆勋，林少辉，等.医药卫生领域人工神经网络研究中

文文献可视化分析[J].海峡预防医学杂志，2021，27（5）：73-76

[5] Sofian K， MOHAMAD A， AZMI A ， et al. Backpropagation

neural network optimization and software defect estimation modelling using a hybrid Salp Swarm optimizer-based Simulated Annealing Algorithm[J]. Knowledge-Based Systems，2022，244

[6] Zhang J X，Qu S R. Optimization of backpropagation

neural network under the adaptive genetic algorithm[J]. COMPLEXITY，2021

[7] Yan C R， Chen Y Z，Wan Y Q， et al. Modeling low- and

high-order feature interactions with FM and self-attention network[J]. Applied Intelligence，2020，51

[8] Chen T，Yin H Z，Zhang X L， et al.Meng. Quaternion

factorization machines： alightweight solution to intricate feature interaction modeling[J]. IEEE transactions on neural networks and learning systems，2021

[9] Fan H Y， Xue  L Y， Song Y， et al.A repetitive feature

selection method based on improved ReliefF for missing data[J]. Applied Intelligence，2022，52（14）

[10] Wang L X， Jiang S Y.A feature selection method via

analysis of relevance， redundancy，and interaction，Expert systems with applications，volume 183，2021，115365

[11] 王丽，陈基漓，谢晓兰，等.基于混沌天牛群算法优化的神经

网络分类模型[J].科学技术与工程，2022，22（12）：4854-4863