一种改进的沙丘猫优化算法求解装箱问题
段敏 代永强 刘欢

摘 要: 针对沙丘猫优化算法容易陷入局部最优的问题,提出一种改进的沙丘猫优化算法。首先通过帐篷混沌为映射模式来增强沙丘猫群体的多样性;然后采用非线性递减模型控制参数,降低了沙丘猫个体的敏感度;为增强沙丘猫的移动能力,引入了高斯随机游走策略,使算法有更强大的全局探索能力。将沙丘猫优化改进算法和其他比较算法用于装箱问题求解,结果表明,沙丘猫优化改进算法在所有算法中代价最小,收敛速度最快。
关键词: 装箱问题; 沙丘猫优化算法; Tent映射; 高斯随机游走策略
中图分类号:TP3 文献标识码:A 文章编号:1006-8228(2023)06-60-05
Improved Sand Cat Swarm Optimization to solve the bin-packing problem
Duan Min, Dai Yongqiang, Liu Huan
(College of Information Science & Technology, Gansu Agricultural University, Lanzhou, Ganshu 730070, China)
Abstract: An improved SCSO is proposed for the problem that SCSO is easy to fall into local optimum. Firstly, the diversity of the Sand Cat Swarm is enhanced by Tent chaos as a mapping model. Then, a nonlinear decreasing model is used to control the parameters, which reduces the sensitivity of individual Sand Cat. Finally, a Gaussian random wandering strategy is introduced to enhance the mobility of Sand Cats, which gives the algorithm a more powerful global exploration capability. The improved SCSO and other comparative algorithms are used to solve the bin-packing problem, and the experimental results show that the improved SCSO has the lowest cost and the fastest convergence speed among all algorithms.
Key words: bin-packing problem; Sand Cat Swarm Optimization (SCSO); Tent mapping; Gaussian randomized wandering strategy
0 引言
1831年Gauss關注到装箱问题(Bing Packing Problem,BPP)的近似算法,开始研究布局问题。上世纪八十年代后期,张国川和越民义开始研究最为经典的FFD算法[1],1991年通过权函数的改良和精准分析将FFD算法近似界的尾项从3降到1并大大缩减了证明的篇幅[8],自此行业内掀起了组合优化问题的广泛讨论[2-5]。装箱问题是计算科学领域中一个非常重要的概念,它见于日常生活中,在现代工业上也被广泛地应用,如服装行业的面料剪裁、快递行业的集装箱货物装载、现实生活中的物品包装以及印刷行业的排样等。同样在计算机科学中装箱问题也发挥了一定的作用,如文件分配、资源分配、任务调度等底层操作,甚至还应用于一些智力游戏中。
自从装箱问题问世以来,不少学者就展开了对这一问题的研究,从现有的研究成果来看,解决装箱问题的算法有两种,即精确算法与启发式算法。精确算法有分支界定法、动态规划法、线性规划法等;启发式算法有禁忌搜索、遗传算法、模拟退火、萤火虫算法等。以上算法在解决装箱问题时取得了一定的成果,但同时也显现出易早熟、后期收敛速度慢等不足。
2022年,土耳其学者Amir Seyyedabbasi和Farzad Kiani提出了沙丘猫优化算法(Sand Cat Swarm Optimization,SCSO),该算法是一种模拟
沙丘猫群沙漠生存行为的元启发式算法[6]。该算法具有参数少、收敛性和鲁棒性较好等特点。但由于该算法提出时间较晚,现在正处于该算法的研究初期阶段。目前关于SCSO的研究较少,且鲜有利用改进的SCSO算法求解离散优化问题。
针对沙丘猫优化算法收敛精度低、易陷入局部最优等问题,本文提出了一种改进的沙丘猫优化算法(ISCSO)并用该算法求解组合优化中一维装箱问题,以此验证该算法的可行性。
1 数学模型的建立
1.1 装箱问题数学模型
有m个待装货物和n个集装箱,在保证使用集装箱最少的情况下,将m个货物装入n个集装箱,同时考虑箱体(或容积)限制等限制条件。在建立模型之前,我们首先给出符号说明:ki为物品i的体积;W为任意一个集装箱的容积;N为集装箱集合,N={1,2,…,n};为集装箱d中已装箱物品集合。具体数学模型如下:
[minf=d∈Nψd] ⑴
[ψd∈0,1; ?d∈N] ⑵
[κi,d∈0,1;?d∈N,?i=1,2,…,m] ⑶
[i=1mwi×κi,d≤W;?d∈N] ⑷
[i=1mκi,d=1; ?d∈N] ⑸
[d∈Nκi,d=1;?i=1,2,???,m] ⑹
其中,式⑴为目标函数,表示使用的集装箱数量最少。式⑵中为0-1变量,表示集装箱d是否被使用,集装箱d被使用为1,反之为0;式⑶中为0-1变量,表示物品i是否会装入集装箱d中,如果物品i会被装入集装箱d,为1,反之为0。式⑷为集装箱的最大容积约束,保证了装入集装箱d的所有物品的体积之和小于集装箱的容积。式⑸、⑹则保证了任何一件物品均被装入集装箱中,且同一物品不会被装入两个集装箱。式⑺限制了下一个装箱到集装箱d的物体体积不能大于集装箱d剩余部分的容积。
1.2 装箱问题的实际约束
在实际装载过程中,物品尺寸、体积、形状、数量以及集装箱的规格等可能是不同的,这在一定程度上增加了集装箱装载的复杂性。针对以上对集装箱装载问题分类以及复杂性的讨论,我们将集装箱装载常用的约束条件和一维装箱问题的变体做如下说明[7]。
⑴ 完整性约束
物品是一个完整的不可再次切割的物体。即同一物体不允许装在不同的集装箱中,具体如式⑸所示。
⑵ 体积约束
货物在装载过程中,其集裝箱的可用体积不停缩小,货物的体积小于等于集装箱的可用体积,货物才可以装入集装箱。具体如式⑺所示。
⑶ 扩展模型
由于在现实生活中,集装箱的规格和费用可能并不相同,如冷藏式集装箱和普通集装箱等,因此,在计算目标函数时需要使集装箱的费用最低,具体如下:
[minf=d∈Nψd+d∈NPd×ψd] ⑺
其中,[ψd]为集装箱d的费用。
2 沙丘猫优化算法(SCSO)
在d维优化问题中,每个沙猫都是一个1?d阵列,每个变量值(x1,x2,…,xd)都是浮点型,且每个x都必须处于上下边界之间,算法运行时首先根据问题的规模,利用沙丘猫群来创建一个候选矩阵。此外,每次迭代都会输出相应的解。若接下来的解更好,则替换当前解决方案。若后续的迭代没有找到更好的解,则不存储本次迭代的解。
在搜索猎物的过程中,假设沙丘猫的听力灵敏范围2kHz,沙丘猫常规灵敏范围将随着迭代过程从2线性的降为0。每只沙丘猫会根据最优解、自己当前的位置和[r]来更新自己位置。位置更新公式如下:
[pos(t+1)=r×(posbc(t)- rand(0,1)×posc(t))] ⑻
其中,[posbc]为最佳候选位置,[posc]为当前位置,[posb]为最佳位置之间的距离,最优位置与当前位置可根据式⑼和式⑽计算。
[posrnd=rand(0,1)×posb(t)-posc(t)] ⑼
[post+1=posbt-r×posrnd×cos(θ)] ⑽
搜索和攻击阶段根据自适应的R和[rg]来保证,当[R≤1]时,SCSO算法强制搜索Agent进行探索,否则,搜索Agent进行探索并寻找猎物。
[Xt+1=Posbt-Posrnd×cosθ×r |R|≤1;r×Posbc(t)-rand(0,1)×Posc(t)R>1;] ⑾
3 沙丘猫优化改进算法(ISCSO)
3.1 Tent映射策略
SCSO算法在初始化的过程中,同绝大多数元启发示算法类似,通过基础语言包随机产生的数据作为种群信息,在这种情况下算法很难保证群体的多元化。在算法优化过程中,初始化物种分布在搜索空间内越均匀,越能有效提高算法的寻优结果[9]。基于以上结论,本文借助Tent映射模型进行种群初始化。Tent映射模型如下:
[xn+1=21-xn12≤xn≤12xn 0≤xn<12] ⑿
3.2 非线性递减策略
在SCSO中,沙丘猫的常规灵敏度范围[rg]不仅控制着搜索和攻击的转换,同时也决定了每只沙丘猫的灵敏度范围。研究发现,沙丘猫的敏感度与算法寻优能力相关,因此,为了提升沙丘猫优化算法跳出局部极值的能力,本文引入了非线性指数递减策略,从而改变沙丘猫灵敏度。详见式⒀、式⒁。
[rg=S-S×tctmax+δ] ⒀
[δ=rand×cosrand0,1×2π*tctmax×sinrand×2π*tctmax-1] ⒁
3.3 高斯随机游走策略
高斯随机游走模型是随机游走模型中较为典型的一种,具有较强的开发能力。在ISCSO的搜索阶段引入高斯随机游走策略,以扰动种群的最优个体[10]。通过此方法,提高了算法的收敛速度,从而使算法能跳出局部最优,弥补算法的早熟缺陷。ISCSO其位置更新策略详见式⒂、式⒃。
[pos(t+1)new=Gaussianposbct,κ+r×(posbc(t)-rand(0,1)×posc(t))] ⒂
[κ=cos(π2×tcπ2)×pos(t)-posbct] ⒃
3.4 改进算法伪代码
(a) 根据式⑿初始化种群
(b) 根据目标函数计算适应度函数
(c) 初始化r,rg,R
(d) WHILE(t<=max)
(e) FOR i in search agent
(f) 根据轮盘赌获取随机角度(0°≤[θ]≤ 360°)
(g) IF(ABS(R)<=1)
(h) 根据式⑼、式⑽获取更新代理的位置
(i) ELSE
(j) 根据式⑿获取更新代理的位置
(k) 用高斯随机游走策略(式⒂、式⒃)来获取新位置
(l) END IF
(m) END FOR
(n) t++
(o) END WHILE
4 仿真实验
4.1 实验环境
仿真实验在64bitWindows11操作系统、Intel(R) Core(TM) i9-12900H 2.50 GHz处理器、16G内存的计算机上进行,算法采用软件MATLABR2021a编译实现。
4.2 算法模拟参数
本文为了评估ISCSO算法与其他优化算法的性能,采用测试函数与求解一维装箱的寻优性能两个方面进行对比。测试函数测试时算法维度D=30,群体规模N=30,迭代次数T=500。对比算法参数选自国外学者Amir Seyyedabbas的沙丘猫优化算法。
4.3 测试函数结果分析与对比
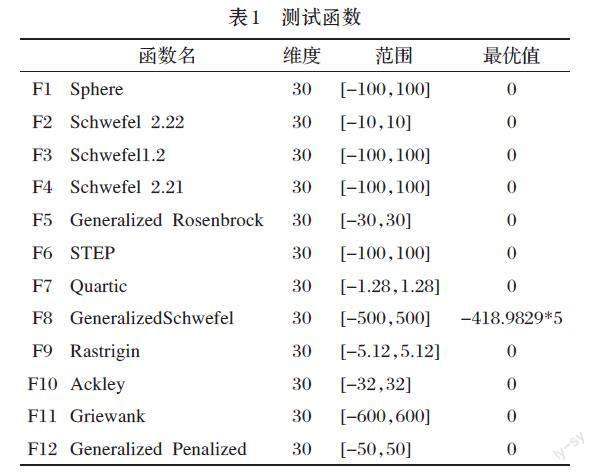
为了比较和分析ISCSO算法与另外三种算法(SCSO、PSO、GWO)的寻优性能,选取CEC2014、CEC2015共12个经典测试函数来验证所提出的优化算法的性能,其中F1~F7为单峰函数,F8~F12为双峰函数。函数表达式详见Amir Seyyedabbas学者的沙丘猫优化算法,其他参数如表1所示。
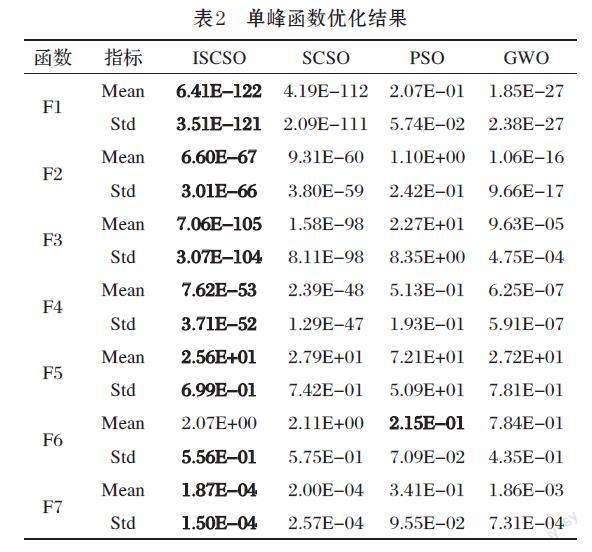
通过表2可知,在30次单独运行时,ISCSO算法在限定的函数评定次数内,较其他三种算法有更好的收敛性,F1~F5、F7的优化精度最高,其中F1函数精度最为明显。在 F5函数下SCSO、GSO和ISCSO算法收敛速度均有较大提高,但ISCSO算法收敛速度最快;针对F6函数的平均差,PSO算法具有最优的收敛性能。
同时通过表3可见 ISCSO对于五种双峰函数的优化结果,针对F8~F11函数,融合于高斯随机游走策略和非线性递减策略,ISCSO算法快速跳出局部最优,收敛于全局最佳,且在 F9、F11上寻找到了最佳值;对于F10函数而言,虽然两类算法都在寻找全局最佳,但ISCSO标准差略胜于SCSO算法。综上所述,ISCSO算法的收敛速度和收敛精度都有明显的提升。
4.4 基于ISCSO算法的装箱问题性能分析
在本节展示了ISCSO算法、FA算法、PSO算法、IWO算法以及GA算法在装箱问题中的应用。其中物品集的体积为{6,3,4,6,8,7,4,7,7,5,5,6,7,7,6,4,8,7,8,8,2,3,4,5,6,8,5,7,7,12},箱子体积为30,最佳值为7。进一步的,我们将五种算法各运行30次,图1、图2以及图3分别展示了五种算法运行30次的过程中目标函数的最优值、平均值以及最差值。
从图1可以看出,当五种算法在30次运行最佳适应度函数最佳值时,ISCSO算法的最佳迭代次数是最少的,仅在第8次迭代便获得了最佳值,与 FA、 GA、PSO和IWO算法相比分别快25%、25%、100%以及3250%。
从图2得出,当五种算法在30次运行平均适应度函数最佳值时,ISCSO算法在第154次迭代便取得了最佳值,分别比FA、GA、PSO和IWO算法快127.27%、20.78%、47.40%以及127.27%。
從图3可见,在五种算法的适应度函数最差的情况下,ISCSO算法的最佳值出现在迭代次数472次内,其余算法在500次循环中均未能找到相应的解。从而得到一个结论,无论在适应函数最优值、最差值还是平均值的情况下,ISCSO算法的求解效果均是最优异的。
5 结论
本文针对装箱问题,融合混沌映射、非线性递减系数和高斯随机游走等机制,提出了一种改进的沙丘猫优化算法(ISCSO)。CEC仿真实验结果表明,ISCSO算法相比较SCSO、PSO、GWO等算法,表现出较好的结果,ISCSO算法在求解装箱问题时相比较PSO、GWO、IWO、GA等算法,具有较好的寻优性和求解精度。在进一步研究过程中,将对一维装箱问题扩展至三维装箱问题,同时考虑物流、海运等实际场景中的约束条件,构建相应的数学模型,并提出对应的改进策略应用ISCSO算法的框架求解多约束的三维装箱问题。
参考文献(References):
[1] 张国川,越民义.TIGHT PERFORMANCE BOUND OF
AFBK BIN PACKING[J].Acta Mathematicae Applicatae Sinica(English Series),1997(4):321-331
[2] Hao X, Zheng L, Li N, et al. Integrated bin packing and lot-
sizing problem considering the configuration-dependent bin packing process[J]. European Journal of Operational Research,2022,303
[3] Dell' AmicoM, Furini F, Iori M. A branch-and-price
algorithm for the temporal bin packing problem[J]. Computers & operations research,2020,114(Feb.):104825.1-104825.16
[4] Martinez-SykoraA, Alvarez-Valdes R, Bennell J, et al.
Matheuristics for the irregular bin packing problem with free rotations[J]. European Journal of Operational Research,2017:S0377221716307950
[5] Lw D, Ml B, Al C, et al. A branch-and-price algorithm for
the two-dimensional vector packing problem[J]. European Journal of Operational Research,2020,281(1):25-35
[6] Seyyedabbasi A, Kiani F. Sand Cat swarm optimization: a
nature-inspired algorithm to solve global optimization problems. EngComput 2022. https://doi.org/10.1007/s00366-022-01604-x.
[7] 張钧,贺可太.求解三维装箱问题的混合遗传模拟退火算法[J].
计算机工程与应用,2019,55(14):32-39,47
[8] 陈婳,张国川.经典一维装箱问题近似算法的研究进展[J].
运筹学学报,2022,26(1):69-84
[9] Sneha P S,SankarS,Kumar A S.A chaotic colour image
encryption scheme combining Walsh-Hadamard transform and Arnold-Tent maps[J]. Journal of ambient intelligence and humanized computing,2020,11(3):1289-1308
[10] Sun C J, Gao F. A Tent Marine Predators Algorithm
with Estimation Distribution Algorithm and Gaussian Random Walk for Continuous Optimization Problems[J]. Computational intelligence and neuroscience,2021(Pt.14):2021

