直流接地极地表电位的切比雪夫多项式求解法
齐桓若 陈晨 闫向阳 康祎龙 王顺然 刁旭


摘要运行经验表明,直流接地极造成电网大范围直流偏磁危害,其根源在地表电位不均匀分布.针对广域深度分层的复杂大地模型关于地表电位分布求解方面的难题,利用切比雪夫多项式拟合地表电位的汉克尔变换核函数.通过切比雪夫多项式的移位运算、系数展开和截断误差判定,得到了核函数的切比雪夫多项式自适应阶数拟合方法,从而大幅降低了直流接地极造成广大区域地表电位分布的计算难度.与标准接地计算软件CDEGS的水平8层结构大地算例对比结果表明,直流接地极入地电流5 kA时,本方法在1~100 km地表范围内的地表电位偏差小于1 V.进一步分析了切比雪夫多项式阶数对地表电位的计算结果的影响,证实了20阶切比雪夫多项式的精度就可以满足一般的直流偏磁风险评估的应用需求.基于移位切比雪夫多项式的地表电位快速评估方法为直流偏磁风险评估提供了一种基础的技术手段,有助于降低电网直流偏磁风险评估的难度.
关键词直流接地极;地表电位;切比雪夫多项式;汉克尔积分;直流偏磁
中图分类号
TM12
文献标志码
A
收稿日期
2021-12-15
资助项目
国家自然科学基金(51607129)
作者简介齐桓若,女,硕士,工程师,主要从事输变电工程设计及基建数字化管理研究.lvteng320@163.com
0 引言
直流输电在单极大地返回运行方式下,高幅值的直流电流会通过直流接地极流入大地.由于大地的不良导电和广域电网的同时作用,会导致部分的直流电流入侵到交流系统,从而产生对变压器的不良影响,即直流偏磁危害.直流偏磁严重危害电力系统安全运行.变压器直流偏磁的耐受特性非常复杂[1-3],直流偏磁的治理也需要耗费大量的人力和物力[4-7].
运行经验表明,电网直流偏磁危害的根源在于直流接地极造成的地表电位不均匀分布[8-11],具体表现为:输电线路连接了相距较远的众多变电站,而变电站内高压变压器中性点多为直接接地的运行方式;大地与电力网之间形成了一个“并联”的电流通道,由于变电站之间的地表电位不同,直流输电的部分入地电流从大地中被“抽取”到电力系统内;直流电流流经变压器绕组,变压器铁芯饱和而产生励磁的半周饱和现象,从而形成直流偏磁危害.直流偏磁危害主要是变压器的振动和异响,以及局部温升和谐波等.
电网偏磁仿真评估采用的是直流电流入侵的场路耦合模型[10],即地上的电路模型与地下的电流场的耦合.该耦合直接表现为电站的地表电位,电站之间的地表电位差异越大,则偏磁的情况越严重.地表电位的求解方法与选取的大地模型有关.由于直流偏磁问题采用的大地模型是实际的地质电性结构模型,所以已有的接地分析评估方法有可能不适用[11-12].文献[13-15]系统地使用有限元方法求解复杂结构大地参数,文献[16-17]提出了考虑地形起伏的地表电位计算方法,文献[18-19]重点研究了地中断裂带分布情况下的地表电位,这些研究主要依赖商用有限元软件,暂无法应用于电网偏磁风险评估.耿山等[20]使用镜像法研究了新疆复杂地质环境下的直流接地极周边地表电位分布,马成廉[21]对模型参数进行灵敏度分析,但镜像法目前还存在计算量大和精度不高的问题,无法推广应用于复杂的地质工况.马成廉[21]较为系统地研究了特高压直流接地极近区地电位分布特征,李嘉思等[22]针对复杂土壤结构下直流接地极选址及直流偏磁风险也开展了相应的评估工作,他们仍沿用复镜像法进行直流接地极地表电位的求解.复镜像算法较为复杂,技术难度较高,不利于推广应用.此外,高速铁路的钢轨电位和地表电位问题[23]、采用地表电位进行接地网的腐蚀诊断[24],以及跨步电压的回声状态网络分析法[25]等均需要求解地表电位,但目前的研究主要依赖商用接地分析软件CDEGS,还缺少公开技术手段的支持.
综上所述,目前的研究过于依赖商用的有限元计算软件和接地计算软件,没有形成可靠的计算工具供使用.针对直流接地极造成广大区域地表电位分布的计算问题,本文提出了一种切比雪夫多项式拟合的快速算法,为直流偏磁风险评估和其他工程问题的应用场景提供了思路和新手段.
1 地表电位的切比雪夫多项式求解法
1.1 地表电位的基础理论
直流接地极造成大范围的地表电位V,可写为如下形式:
V(r)=ρ 1I2π∫∞ 0k 1J 0(λr)dλ, (1)
其中,r为地表观察点与直流接地极的距离(r远大于直流接地极的尺寸),ρ 1为首层大地的电阻率,I为直流输电系统的大地返回电流,J 0为第一类零阶贝塞尔函数,λ为积分系数,k 1为表征水平分层大地结构的等效电阻率函数,可由递推公式求解:
k n-1=1-μ n-1exp(-2λd n-1)1+μ n-1exp(-2λd n-1),μ n-1=ρ n-1-ρ nρ n-1+ρ n,…k i=1-μ iexp(-2λd n-1)1+μ iexp(-2λd n-1),μ i=ρ i-ρ i+1k i+1ρ i+ρ i+1·k i+1,…k 1=1-μ 1exp(-2λd n-1)1+μ 1exp(-2λd n-1),μ 1=ρ 1-ρ 2k 2ρ 1+ρ 2k 2,(2)
其中,水平分層大地结构示意如图1所示,d为分层的厚度,ρ为分层的电阻率,μ i为第i个分层的反射系数.
式(1)属于广义无穷积分,又称汉克尔变换,k 1为汉克尔变换的积分核函数.由于J 0随rλ的增大呈现震荡衰减的特性,所以传统的数值计算方法无法准确求解式(1).如果k 1可以进行无穷指数级数展开,那么式(1)可以运用经典镜像法求解,但无法针对分层较多的情况作求解.主要是因为分层较多时k 1的无穷指数级数理论表达过于复杂,且计算时间太长,无法用于实际.
式(1)为场源点均在地表的情况.对于场源点任意位置的情况,只需将V(r)积分式替换为实际的情况即可,具体见文献[11-12].
1.2 切比雪夫多项式求解方法
切比雪夫多项式为满足如下二阶微分方程的解:
(1-x2)d2ydx2-xdydx+n2y2=0. (3)
本文是基于第一类切比雪夫多项式开展研究的.第一类切比雪夫多项式T:
T 0(x)=1, (4)
T n(x)=2n-1∑[0.5n]k=0(-1)n(n-k-1)!k!22k(n-2k)!xn-2k, (5)
式中[0.5n]表示对0.5n向下取整.
如果f(x)为区间[-1,1]内的连续函数,则可将它转为T的无穷级数:
f(x)=0.5c 0+∑∞n=1c nT n(x), (6)
c n=2π∫0 -1f(x)T n(x)1-x2dx, (7)
式(6)又称为傅里叶-切比雪夫级数展开法.
切比雪夫多项式求解方法的基本思想是利用切比雪夫多项式将地表电位无穷积分转为有限长度切比雪夫序列求和,进而快速评估地表电位.切比雪夫多项式求解方法如下:
步骤1.设首层的衰减系数E为
E=exp(-2λd 1). (8)
对于第i层大地,其衰减系数可以改写为
Eδ i=exp(-2λd i),δ i=d id 1. (9)
步骤2.将式(8)、(9)代入式(2),可得
k n-1=1-μ n-1Eδ n-11+μ n-1Eδ n-1,μ n-1=ρ n-1-ρ nρ n-1+ρ n,…k i=1-μ iEδ i1+μ iEδ i,μ i=ρ i-ρ i+1k i+1ρ i+ρ i+1k i+1,…k 1=1-μ 1Eδ 11+μ 1Eδ 1,μ 1=ρ 1-ρ 2k 2ρ 1+ρ 2k 2, (10)
使用级数展开,式(10)可以化为
1-μ 1Eδ 11+μ 1Eδ 1≈A 0+A 1E+A 2E2+…=∑mi=0A iEi. (11)
引入移位运算、系数展开和截断误差判定等三大环节来求解式(11):
1)移位运算.切比雪夫多项式的值域范围为[-1,1],而系数k 1的取值范围为[0,1].因此切比雪夫多项式要作移位运算,移位切比雪夫多项式T j表达式取为
T 0(E)=1,T 1(E)=2E-1,T 2(E)=8E2-8E+1,T 3(E)=32E3-48E2+18E-1,T 4(E)=128E4-256E3+160E2-32E+1,…T m+1(E)=2·(2E-1)·T m(E)-T m-1(E), m≥1. (12)
2)系数展开.进行k 1的移位切比雪夫多项式展开,式(11)转化为
k 1(E)≈-0.5c 0+∑nk=0c kT k(E)→ A 0+A 1E+A 2E2+…,(13)
其中,c j为T j的系数,c j的具体表达式为
c j=2m∑mb=0k 1(ξ b)cosπjb+0.5m+1, (14)
其中,ξ b为T b系数方程的根,ξ b的具体表达式为
ξ b=0.5+0.5cosπb+0.5m+1,b=0,1,…,m. (15)
3)截断误差判定.m阶移位切比雪夫多项式表达式的误差表达式可写为
ε m(E)=∑∞b=m+1c bT b(E). (16)
式(16)近似取误差主项:
ε m(E)≈c m+1T m+1(E), (17)
E值域误差的总误差为
ε tot≈∫1 0c b+1T b+1(E)dE, (18)
式(18)积分的理论结果为
ε tot≈2m+1∑m+1b=0k 1(ξ b)cosπ(b+0.5)(m+1)m+2·
∑m+1i=0t ii+1, (19)
式中,t i为式(12)中移位切比雪夫多项式的系数.
因此可按图2所示流程确定式(13)中的最高阶数m.
步骤3.式(11)代入式(1)有
V(r)=ρ 1I2π∫∞ 0∑ni=0A iEiJ 0(λr)dλ. (20)
根據利普希茨积分公式
∫∞ 0exp(-λ|x|)J 0(λy)dλ=1x2+y2, (21)
代入式(20)有
V(r)=ρ 1I2π∫∞ 0∑ni=0A iEiJ 0(λr)dλ=
ρ 1I2π∑ni=0A i4i2d2 1+r2. (22)
输入电流I,求解式(22),输出计算结果.
切比雪夫多项式求解方法大幅降低了直流输电大地返回电流造成地表电位分布的计算难度,并有助于形成计算软件.
2 算例分析与对比
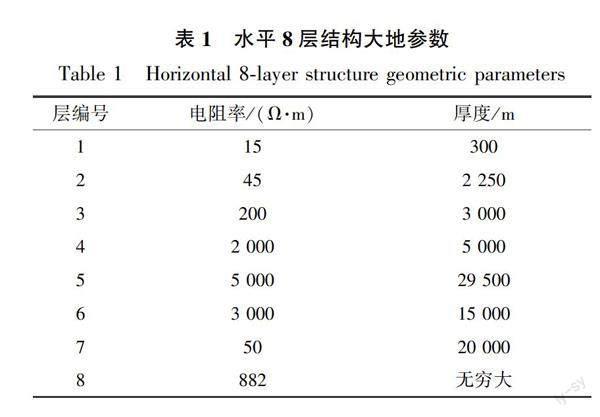
取水平8层结构大地(参数见表1)的算例,引入了标准接地计算软件CDEGS关于5 000 A点电流源在1~100 km地表范围内的电位的计算结果,并与20阶的切比雪夫多项式方法作对比.两种不同方法的地表电位分布如图3所示.本文方法与CDEGS计算结果在1 km处的偏差为0.71 V,10 km处的偏差为0.13 V,100 km处的偏差为0.04V.
由于切比雪夫多项式方法的计算精度和收敛速度与阶数紧密相关,所以表2给出了不同阶数下关于表1土壤模型的不同观测点地表电位的结果.从表2的结果可以看出,在阶数为10阶的情况下计算结果偏差较大,但阶数到达20阶及以上时,计算结果趋于稳定.在1~100 km的范围内,即使是20阶的切比雪夫多项式方法,也已经达到足够工程应用精度.
为进一步分析表2中的数值差异,本文针对表1的情况,将切比雪夫多项式拟合误差式(19)进行了更深入的计算分析,结果如表3所示.从表3可以看出,刚开始随着切比雪夫多项式阶数的增加,核函数拟合的理论偏差迅速衰减,然而当阶数达到20阶时,收敛速度趋于缓慢.本文的应用情况表明,切比雪夫多项式的阶数只要选取为误差较小的情况就可以达到比较好的工程应用效果,计算的速度也较快.盲目地提高阶数并不能够为计算的结果带来明显的精度提升,反而会浪费大量的计算时间.
3 结论
针对直流接地極造成地表电位分布求解方面的难题,本文提出了一种切比雪夫多项式拟合地表电位的汉克尔变换积分核函数的求解方法.
1)基本积分核函数的傅里叶-切比雪夫级数展开,引入移位运算、系数展开和截断误差判定等三大环节进行求解,得到核函数的切比雪夫多项式自适应阶数拟合方法,从而大幅降低了地表电位分布的计算难度.
2)通过水平8层结构大地算例分析了切比雪夫多项式阶数m对计算结果的影响.结果表明,在场点-源点距离小于10 m的情况下,切比雪夫多项式阶数需要取40阶,场点-源点距离大于1 km时,取20阶即可达到精度要求.通过与基准接地软件CDEGS的对比,验证了本文方法的准确性.
3)基于移位切比雪夫多项式的地表电位求解方法为直流偏磁风险评估提供了一种基础的技术手段,有助于降低电网直流偏磁风险评估的难度,辅助直流偏磁风险评估等相关工作,可以为电力系统接地设计和其他行业提供相关的技术支持.
参考文献
References
[1] 王泽忠,刘恪,李明洋,等.特高压变压器直流偏磁“三变”联合仿真分析[J].高电压技术,2020,46(12):4097-4105
WANG Zezhong,LIU Ke,LI Mingyang,et al.Co-simulation and analysis of “three transformers” for UHV transformer under DC-bias[J].High Voltage Engineering,2020,46(12):4097-4105
[2] 郭满生.变压器耐受直流偏磁电流数值的一点考虑[J].变压器,2021,58(3):15-21
GUO Mansheng.A consideration of allowable DC bias current of large power transformers[J].Transformer,2021,58(3):15-21
[3] 李明洋,张俊双,李海明,等.500 kV单相自耦变压器空载直流偏磁下的损耗和温升试验及分析[J].高压电器,2021,57(6):132-139
LI Mingyang,ZHANG Junshuang,LI Haiming,et al.Loss and temperature rise test and analysis on 500 kV single-phase auto-transformer under no-load DC bias[J].High Voltage Apparatus,2021,57(6):132-139
[4] 戎子睿,马书民,林湘宁,等.一种多接地极主动互联及隔直装置协同的直流偏磁治理策略[J].电网技术,2021,45(9):3453-3462
RONG Zirui,MA Shumin,LIN Xiangning,et al.Suppression strategy of DC bias based on coordination between grounding electrodes interconnecting and DC blocking devices[J].Power System Technology,2021,45(9):3453-3462
[5] Pan Z H,Wang X M,Tan B,et al.Potential compensation method for restraining the DC bias of transformers during HVDC monopolar operation[J].IEEE Transactions on Power Delivery,2016,31(1):103-111
[6] Xie Z C,Lin X N,Zhang Z Y,et al.Advanced DC bias suppression strategy based on finite DC blocking devices[J].IEEE Transactions on Power Delivery,2017,32(6):2500-2509
[7] Wang Z X,Xie Z C,Liu C,et al.Novel DC bias suppression device based on adjustable parallel resistances[J].IEEE Transactions on Power Delivery,2018,33(4):1787-1797
[8] 刘连光,马成廉.基于有限元方法的直流输电接地极多层土壤地电位分布计算[J].电力系统保护与控制,2015,43(18):1-5
LIU Lianguang,MA Chenglian.Calculation of multi-layer soil earth surface potential distribution of HVDC due to finite element method[J].Power System Protection and Control,2015,43(18):1-5
[9] 付振兴,谭捍东,刘慧芳,等.高压直流圆环形接地极电位数值模拟及影响因素分析[J].电网技术,2016,40(6):1909-1915
FU Zhenxing,TAN Handong,LIU Huifang,et al.Potential numerical simulation and analysis of influencing factors of toroidal HVDC grounding electrode[J].Power System Technology,2016,40(6):1909-1915
[10] Pan Z H,Zhang L,Wang X M,et al.HVDC ground return current modeling in AC systems considering mutual resistances[J].IEEE Transactions on Power Delivery,2016,31(1):165-173
[11] Li W,Pan Z H,Lu H L,et al.Influence of deep earth resistivity on HVDC ground-return currents distribution[J].IEEE Transactions on Power Delivery,2017,32(4):1844-1851
[12] 潘卓洪,李嘉思,刘曳君,等.分层土壤接地格林函数的多精度多分辨率计算[J].中国电机工程学报,2019,39(15):4451-4459
PAN Zhuohong,LI Jiasi,LIU Yejun,et al.Multi-precision-resolution computation of the Greens function for the grounding problems of layered soils[J].Proceedings of the CSEE,2019,39(15):4451-4459
[13] 马成廉,刘连光,王乐天,等.高压直流输电接地极地电位分布ANSYS仿真[J].电网与清洁能源,2017,33(4):19-26,33
MA Chenglian,LIU Lianguang,WANG Letian,et al.The ANSYS simulation of HVDC grounding electrode potential distribution[J].Advances of Power System & Hydroelectric Engineering,2017,33(4):19-26,33
[14] 劉连光,姜克如,李洋,等.直流接地极近区三维大地电阻率模型建立方法[J].中国电机工程学报,2018,38(6):1622-1630,1898
LIU Lianguang,JIANG Keru,LI Yang,et al.Three-dimensional earth resistivity structure modelling around DC ground electrode[J].Proceedings of the CSEE,2018,38(6):1622-1630,1898
[15] 李景丽,栗超超,冯鹏.复杂土壤结构对流入变压器直流电流的影响分析[J].电瓷避雷器,2020(3):34-42
LI Jingli,LI Chaochao,FENG Peng.Analysis of the influence of complex soil structure on DC current flowing into transformer[J].Insulators and Surge Arresters,2020(3):34-42
[16] 司马文霞,罗东辉,袁涛,等.地表垂直落差对接地网接地电阻测量的影响及改善措施[J].高电压技术,2018,44(5):1490-1498
SIMA Wenxia,LUO Donghui,YUAN Tao,et al.Influence of vertical drop of soil on grounding resistance measurement of grounding grid and the improvement measures[J].High Voltage Engineering,2018,44(5):1490-1498
[17] 熊奇,王沐雪,黄浩,等.复杂地质情况下接地极土壤模型建立及研究[J].中国电机工程学报,2020,40(7):2269-2277,2405
XIONG Qi,WANG Muxue,HUANG Hao,et al.Establishment of earth model for HVDC earth electrode in complicated terrain[J].Proceedings of the CSEE,2020,40(7):2269-2277,2405
[18] 郭名文,樊艳芳,耿山,等.特高压直流接地极周边断裂结构对地表电位分布的影响研究[J].电力系统保护与控制,2019,47(2):73-79
GUO Mingwen,FAN Yanfang,GENG Shan,et al.Study on the effect of fracture structure adjacent to ground electrodes of UHVDC power transmission lines on earth surface potential distribution[J].Power System Protection and Control,2019,47(2):73-79
[19] 李景麗,栗超超,冯鹏.异阻层状土壤对HVDC接地极散流性能的影响分析[J].电瓷避雷器,2020(2):1-9
LI Jingli,LI Chaochao,FENG Peng.Analysis of layered soil resistance effect on HVDC grounding diffuser performance[J].Insulators and Surge Arresters,2020(2):1-9
[20] 耿山,樊艳芳,巩晓玲,等.特高压直流接地极周边地表电位分布计算与敏感性参数研究[J].高压电器,2019,55(3):163-169
GENG Shan,FAN Yanfang,GONG Xiaoling,et al.Calculation of earth surface potential around UHVDC grounding electrode and analysis on sensitive parameters[J].High Voltage Apparatus,2019,55(3):163-169
[21] 马成廉.特高压直流接地极近区地电位分布特征研究[D].北京:华北电力大学(北京),2020
MA Chenglian.Research on distribution characteristics of earth potential near UHVDC grounding electrode[D].Beijing:North China Electric Power University,2020
[22] 李嘉思,刘曳君,潘卓洪,等.复杂土壤结构下直流接地极选址及直流偏磁风险评估[J].电测与仪表,2021,58(2):13-18
LI Jiasi,LIU Yejun,PAN Zhuohong,et al.Site selection of DC grounding electrodes in complex soil and risk assessment of DC bias[J].Electrical Measurement & Instrumentation,2021,58(2):13-18
[23] 熊骜寒.高速铁路不同路段综合接地系统钢轨电位与地表电位分析[D].成都:西南交通大学,2017
XIONG Aohan.Analysis of rail potential and surface potential of integrated grounding system in different sections of high speed railway[D].Chengdu:Southwest Jiaotong University,2017
[24] 王丰华,王劭菁,刘亚东,等.采用地表电位和磁感应强度进行变电站接地网故障诊断的效果对比[J].高电压技术,2016,42(7):2281-2289
WANG Fenghua,WANG Shaojing,LIU Yadong,et al.Comparison of substation grounding grid fault diagnosis results using surface potential and magnetic induction intensity[J].High Voltage Engineering,2016,42(7):2281-2289
[25] 盛青,王丰华,盛连军,等.基于回声状态网络的接地网地表电位计算[J].高压电器,2019,55(3):144-149,154
SHENG Qing,WANG Fenghua,SHENG Lianjun,et al.Calculation of surface potential distribution of grounding grid based on echo state network[J].High Voltage Apparatus,2019,55(3):144-149,154
Solving surface potential of DC grounding electrode by Chebyshev polynomial
QI Huanruo1 CHEN Chen1 YAN Xiangyang1 KANG Yilong1 WANG Shunran1 DIAO Xu1
1Economic and Technological Research Institute of State Grid Henan Electric Power Company,Zhengzhou 450052
Abstract The operation experiences have shown that the large-scale DC magnetic bias caused by DC grounding electrode can be attributed to the uneven surface potential distribution.Here,the Chebyshev polynomial is used to fit the Hankel transform kernel function in order to solve the surface potential distribution for the complex earth model of wide area depth stratification.The adaptive order fitting method of Chebyshev polynomial for kernel function is obtained via shift operation,coefficient expansion and truncation error determination,which greatly reduces the calculation difficulty of surface potential distribution in a large area caused by DC grounding electrode.Compared with the standard grounding calculation software CDEGS,the proposed Chebyshev polynomial approach achieves less than 1 V of earth surface potential deviation in range of 1-100 km when the DC grounding current is 5 000 A.Moreover,the order of the Chebyshev polynomial has influence on the solution results,and it is confirmed that the 20th-order Chebyshev polynomial can meet the accuracy requirements for general DC bias risk assessment.The proposed surface potential assessment method based on shifted Chebyshev polynomial provides a basic technical means for the risk assessment of DC bias,which is helpful to reduce the difficulty of DC bias risk assessment for power grid.
Key words DC grounding electrode;surface potential;Chebyshev polynomial;Hankel integral;DC bias

