例析几何证明中逻辑推理的典型错误

颜胤豪

【摘要】推理与证明是数学活动中的重要组成，也是培养学生推理能力的重要途径.但由于受到多种因素的制约，学生在解决几何证明题目时常面临诸多逻辑推理典型错误，阻碍学生逻辑推理能力的培养.本文结合全等三角形证明的题目，对其进行详细的探究.

【关键词】初中数学；全等三角形；几何证明

在最新的《义务教育数学课程标准》中，不仅明确了“图形与几何”这一核心目标，还明确了“培养学生逻辑推理能力”要求.在数学学习中，全等三角形的证明不仅是中学数学的重要组成部分，也是培养学生推理与证明的典型内容.但是学生在解决这些问题的过程中，还存在不少问题，不仅制约了学生的解题效率，也阻碍了学生逻辑思维能力的发展.鉴于此，本文以学生在全等三角形几何证明中逻辑推理典型错误作为课堂教学资源，分析其产生的原因，并提出相应的教学策略，旨在提升学生的解题能力，并在解题中培养和发展学生的逻辑推理能力和素养.

1 任意推理、引申定理

部分学生在“全等三角形”学习中，由于并未真正理解相关的几何概念和定理，致使在证明相关题目的时候，对教材中的定理进行任意引申、推广，进而得出“假判断”，并将其作为证明的根据.在这种情况下，学生在证明题目时，常常因为“虚假理由”，出现各种各样的错误.

例1 已知：如图1所示，已知△ABC，AB=AC，AD为∠BAC的平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，求证：AD为EF的垂直平分线.

学生在对这一题目进行证明时，常常出现一定的错误：因为AD为∠BAC的平分线，DE⊥AB，DF⊥AC，所以DF=DE（角平分线上的点到两边的距离相等），因此得出AD为线段EF的中垂线.从表面上来说，这一证明过程中则存在一定的错误，结合所学的定理，只能证明D仅仅是EF垂直平分线上的一个点，而过点D则可做出无数条直线.因此，从这一方面上来说，根本无法证明AD就是EF的垂直平分线.

在具体解题实践中，这种错误尤为常见.其主要原因就是学生在证明题目时，无法跨越虚假命题的现象.鉴于此，在日常教学中，必须要引导学生关注几何概念、定理解读，真正将其“吃透、弄懂”，最大限度避免解题中出现的错误.

2 未挖掘题目中蕴含的条件

学生在对“全等三角形”相关题目进行证明时，常常会陷入到循环论证中.在这种证明模式下，学生常常是利用需要证明的命题本身，或者等价命题作为证明的根据，但在证明中并未对命题进行证明.

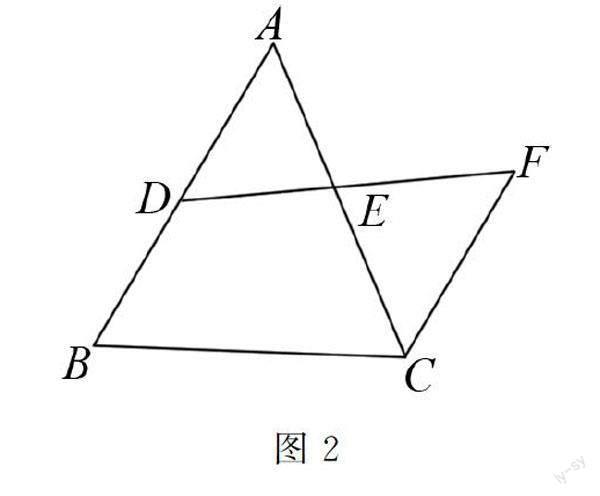
例2 如图2所示，已知△ABC中，D是AB边上的一点，且DF交AC于点E，DE=FE，AE=CE，AB与CF存在什么样的位置关系？对其进行判断且证明.

学生在证明这一问题时，常常会进入到循环论证中：因为DE=FE，AE=CE，所以AD=CF，学生直接将其作为命题的已知条件；又因为AD=CF，DE=FE，AE=CE，所以△AED≌△CEF；又因为∠AED与∠CEF为对顶角，所以AD∥CF，AB∥CF.这一证明题目虽然非常简单，并且证明的思路比较清晰，但部分学生在证明时，依然会进入到上述的“循环论证”中，错误地将AD=CF作为已知条件，将其作为证明的根据，忽视了题目中∠AED与∠CEF是对顶角的隐含条件.在这种情况下，学生在证明的时候，难免会出现错误.

在日常证明教学中，为了避免这一错误，教师可充分发挥自身的引导作用，使学生在日常做题时逐渐养成认真审题的习惯，并结合典型的例题引导学生充分挖掘其中的隐含条件，进而顺利解决几何证明题目，降低错误的发生率.

3 偷换命题，运用特殊代替一般

部分学生在证明“全等三角形”时，为了降低证明的难度，常常会将“一般”进行转化，使其成为“特殊”.但这就等于偷换了命题，违反了逻辑上的关系，致使学生在证明的时候，常常出现相关的错误.

例3 求证：三角形一边上的中线小于其他两边之和的一半.

部分學生在证明时，如图3所示，△ABC与△A′BC是全等三角形.在这一过程中，学生就偷换了概念，将题目中的三角形进行了转化，使其成为全等三角形.之后，连接AA′，与BC相交于D点，则AA′=2AD.在这一步骤中，就将AA′和BC的交点D视为中点；之后，证明出△ABC≌△A′BC，所以AC=A′B.又因为AA′＜AB+A′B，则AA′＜AB+AC，所以2AD＜AB+AC，即AD＜1／2（AB+AC）.学生在证明这一命题的过程中，虽然明确了运用“三角形第三边小于两边之和”的定理，但在具体证明的过程中，则出现了“偷换命题”的现象，即将三角形偷换为全等三角形，将AA′和BC的交点错误地当作中点.在这种情况下，由于学生运用特殊代替了一般情况，致使其在证明的过程中，极容易出现各种各样的错误.

鉴于此，教师在日常几何证明题教学时，就可充分借助一些典型的例题，使得学生在典型例题分析中，认识到“偷换命题”的问题，使其在日后做题训练中，能够有效避免这一类的错误.

4 结语

综上所述，在“全等三角形”的证明题中，学生在做题训练过程中，常常会因为肆意引申定理、忽视题目中的隐含条件、偷换命题等，致使解题中出现各种各样的错误.鉴于此，在日常解题训练中，教师应通过日常教学引导、典型例题分析，使得学生逐渐掌握相关的解题技巧，并在解题训练的过程中，发展自身的逻辑推理能力和素养.