基于ERWOA 的多输出MPRM 电路面积优化
何俊才,何振学,*,王福顺,霍志胜,肖利民
(1.河北农业大学 智能农业装备研究院,保定 071001;2.河北农业大学 河北省农业大数据重点实验室,保定 071001;
3.北京航空航天大学 高性能计算平台,北京 100191;4.北京航空航天大学 软件学院,北京 100191;5.北京航空航天大学 计算机学院,北京 100191)
逻辑函数可以使用Boolean 逻辑表示或使用(Reed-Muller, RM)逻 辑 表 示[1]。Boolean 逻 辑 表 达式是以AND/OR/NOT 为运算基础,而RM 逻辑表达式是以AND/XOR 为运算基础[2]。对部分电路来说,RM 逻辑电路在面积、功耗、可测试性等方面比Boolean 逻辑电路更有优势[3-4]。混合极性Reed-Muller(mixed polarity Reed-Muller, MPRM)逻辑电路优化得到了广泛关注,并已成为集成电路设计领域的研究热点[5-6]。
n输入变量的Boolean 逻辑电路有 3n个MPRM电路表达式[7],对应着 3n个不同极性。表达式所含与项个数多少决定了MPRM 电路的面积大小[8]。因此,在 3n个MPRM 表达式中寻找一个与项个数最少的MPRM 表达式属于组合优化问题[9]。李辉等[9-10]利用模拟退火遗传算法和枚举法求解多输出MPRM电路面积。卜登立等[11]利用遗传算法解决多输出MPRM 电路面积与SER 折中优化,用混合多值离散粒子群算法解决多输出MPRM 电路面积优化问题[12],得到了较好的效果,但是还存在收敛速度较慢的问题。实际电路大多都是多输出电路,而现有多输出MPRM 电路面积优化研究较少。因此,研究多输出MPRM 电路面积优化具有重要意义和应用价值。
澳大利亚学者Mirjalili 于2016 年提出了一种新的启发式群体智能算法—鲸鱼优化算法(whale optimization algorithm, WOA)[13]。鲸鱼优化算法具有原理简单、易于计算机编程实现和参数较少的优点[14]。鲸鱼优化算法已成功应用于大规模函数优化[14]、0-1 背包[15]、云计算资源调度[16]、噪声图像边缘检测[17]等问题。然而,传统鲸鱼优化算法无法直接用于求解多输出MPRM 面积优化这样的三值组合优化问题。
针对上述问题,本文提出一种多输出MPRM 电路面积优化方法。与现有多输出MPRM 电路面积优化方法相比,本文的主要创新点如下:
1)提出一种基于爆炸机制和重启机制的鲸鱼优化算法(explosion strategy and restart strategy based whale optimization algorithm, ERWOA)。爆炸机制提高了鲸鱼优化算法的收敛速度,重启机制提高了算法的稳定性。
2)提出一种基于二叉树的极性转换算法。因为二叉树的查找效率较高,所以本文基于二叉树来描述多输出MPRM 电路,以提高多输出MPRM 电路的极性转换效率。
3)提出一种多输出MPRM 电路面积优化方法。该方法基于改进的鲸鱼优化算法和改进的极性转换算法来搜索含与项个数最少的多输出MPRM电路,以实现多输出MPRM 电路面积优化。
1 基础知识
1.1 多输出MPRM 表达式
一个输入变量位数为n和输出变量位数为m的Boolean 函 数 系 统F={0,1}n→{0,1}m[18]由m个(1)[8]所示的n输入变量位的Boolean 函数对应的乘积和的标准形表示。
式中:Xi为 最小项表达式;ai为 第i个最小项是否存在,1 为存在,0 为不存在。
任意输入变量位数为n的单输出Boolean 逻辑函数都可以由基于AND/XOR 的MPRM 展开式表示,即[8]
式中:P为MPRM 表达式的极性;πi为与项。
因此,一个输入变量位数为n且输出变量位数为m的MPRM 表达式可表示为
式中:f tp(xn−1,xn−2,xn−3,···,x0)[8]为第t位输出变量的MPRM 表达式。
1.2 极 性
在 多 输 出MPRM 表 达 式 中,πi可 以 展 开 为x˙n−1,x˙n−2,x˙n−3,···,x˙0,极性和式(2)中的下标i共同决定了x˙k的 表现形式。当 (pk,ik) (0 ≤k 例如,给定一个3 输入和2 输出的Boolean 逻辑函数表达式,如下: 其对应极性为0(000)3的MPRM 表达式为 其对应极性为26(222)3的MPRM 表达式为 可以看出,极性为 0(000)3的MPRM 表达式含有6 个与项,极性为 26(222)3的MPRM 表达式含有5 个与项。因此,对于同一电路来说,极性不同,对应的MPRM 表达式所含有的与项个数也不同。多输出MPRM 电路面积优化是在极性优化空间中搜索对应电路面积最小的最佳极性,故多输出MPRM电路面积优化属于组合优化问题。 基于列表技术的混合极性转换算法[8],本文提出一种基于二叉树的极性转换算法,该算法的主要步骤如下: 步骤 1将n个输入变量和m个输出变量的Boolean 逻辑函数展开成最小项表达式,并将最小项表达式存放在2 棵二叉树中,分别记为A-Ⅰ树和A-Ⅱ树。令i=0,目标极性为P。 步骤 2若Pi=2,则跳转到步骤6。否则根据Pi的 值在A-Ⅰ树的第i层 节点中找到和Pi相等的权值边,并将这条边的权值取反。 步骤 3记录A-Ⅰ树中从根节点到叶节点的路径中权值改变过的路径(最小项),在A-Ⅱ树中查找A-Ⅰ树中新生成的最小项是否存在于A-Ⅱ树中。如果A-Ⅱ树中不存在,则将新生成的最小项加入A-Ⅱ树。否则将A-Ⅰ树中新生成的最小项的输出项和A-Ⅱ树中相同的最小项的输出项按位异或,如果异或值为0,则将A-Ⅱ树中对应的最小项删除,否则用异或结果替换A-Ⅱ树中对应最小项的输出项。 步骤 4如果Pi= 1,则将A-Ⅱ树中第i层节点的所有权值取反。否则不进行任何处理。 步骤 5释放A-Ⅰ树。如果i+1 步骤 6i+ +,如果i 基于列表技术的极性间转换算法[8],本文提出一种基于二叉树的极性间转换算法,该算法主要步骤如下: 步骤 1将n个输入变量和m个输出变量且极性为P的MPRM 表达式以二叉树的形式表示出来,分别存放在A-Ⅰ树和A-Ⅱ树上。令i=0,目标极性为T。 步骤 2Xi=Pi⊕Ti。如果Xi=0,转步骤6。如果Xi= 1 或者当Xi= 3 时Pi= 2,将A-Ⅰ树第i层节点中权值为1 的边的权值修改为0。如果Xi=2 或者当Xi= 3 时Pi= 1,将A-Ⅰ树第i层节点中权值为0 的边的权值修改为1。 步骤 3判断A-Ⅰ树中新生成的与项在A-Ⅱ树中是否存在。如果不存在,将与项存进A-Ⅱ树,否则将A-Ⅰ树中新生成的与项的输出项和A-Ⅱ树中相同与项的输出项按位异或。如果异或值为0,则将A-Ⅱ树中对应的与项删除,否则用异或值把A-Ⅱ树中对应与项的输出项替换掉。 步骤 4如果Xi= 3,把A-Ⅱ树中第i层节点的所有权值取反。 步骤 5释放A-Ⅰ树,如果i+1 步骤 6i++,如果i 多输出MPRM 电路面积优化属于组合优化问题。现有多输出MPRM 电路面积优化方法存在收敛速度较慢的问题。因此,在鲸鱼优化算法的基础上,提出一种基于爆炸机制和重启机制的鲸鱼优化算法。此外,提出一种多输出MPRM 电路面积优化方法,该方法使用鲸鱼优化算法搜索面积最小的最佳极性,以实现多输出MPRM 电路面积优化。 鲸鱼优化算法是针对连续问题提出的,不能直接处理像多输出MPRM 电路优化这样的三值组合优化问题。因此,本节提出一种基于爆炸机制和重启机制的鲸鱼优化算法。引入爆炸机制以提高算法的收敛速度,引入重启机制提升算法的稳定性。 3.1.1 编码方案 根据多输出MPRM 表达式的特点,将极性作为鲸鱼个体,并且编码为三进制。若逻辑电路的输入变量位数为n,则解空间的维度为n。 3.1.2 面积模型和适应度函数 以多输出MPRM 表达式含有的与项个数作为面积模型[8]。适应度函数的值等于通过面积模型得到的值。 3.1.3 包围猎物 在包围猎物阶段,由于个体位置更新以后的位置可以在目标猎物和个体位置之间的任何一个位置,因此,在包围猎物阶段只需保证个体和猎物之间的距离不再扩大即可。具体的操作如下: 式中:randInt(0,2)表示随机生成一个属于集合{0,1,2}的数;Xid(t)为 第i个 体第d维的位置;X∗d(t)为猎物第d维的位置。 3.1.4 螺旋泡沫网攻击 在螺旋泡沫网阶段,鲸鱼个体需要不断地向猎物靠近。随机选择一个猎物和个体维度值不相同的维度d,使个体和猎物第d维的值保持一致。 式中:r为一个随机数,表示在鲸鱼个体Xi(t)和猎物X∗(t)的所有值不相同的维度上随机产生的一个数。 流言:前不久,网上流传了一篇文章《咬破舌头1个月得癌!医生的提醒为所有人敲响警钟》,说的是在某大学附属医院的口腔医疗中心,收治了一位65岁的男性舌癌病人,其病因竟然是吃饭咬破了舌头引起的。 3.1.5 随机搜索 在随机搜索阶段,随机选择一个个体作为猎物并靠近。具体操作如下: 在大量实验中发现,鲸鱼优化算法针对中大规模电路优化存在如下现象:从当前最优解搜索到下一个解往往只需要在当前最优解的基础上变换几个维度就能找到一个更优的解。因此,只要在最优解的附近进行大量的搜索,就有可能找到比当前最优解更优的解,进而提高算法的收敛速度。但是鲸鱼优化算法存在从当前最优解搜索到下一个更优解收敛速度不快的问题。由于烟花算法[19]的爆炸机制有很强的局部爆发能力[20],将烟花算法的爆炸思想引入鲸鱼优化算法,以提升算法的局部搜索能力。主要操作如下:假设爆炸半径为r2,需要生成的火花数为n。生成一个火花时,以最优解为基准,随机选择r维,然后在r维上随机生成属于集合{0,1,2}的随机数,重复执行n次,直到生成n个火花。最后评估生成的n个火花的适应度值。图1 为爆炸半径为2,生成一个火花的过程。 图1 爆炸过程Fig.1 Explosion process 在传统鲸鱼优化算法中,存在2 个问题:①在种群质量极差的情况下,经过离散后的原始鲸鱼优化算法可能存在不迭代的情况,导致算法在20 次的重复运行过程中可能存在鲸鱼优化算法最终找到的最优值相差较大的情况。②原始鲸鱼优化算法容易陷入局部最优。以图1 为例,假设极性B是理论上的最佳极性,鲸鱼优化算法要从极性A搜索到极性B需要将极性A中的第1 位的1 变为2,第2 位的2 变为1。当维数较低时,鲸鱼优化算法很容易从极性A搜索到极性B。如果极性A和极性B的维数增加,且从极性A到极性B需要改变的维数越多,鲸鱼优化算法很难在有限次的迭代过程中从极性A搜索到极性B。因此,受文献[21]的启发引入重启机制,当鲸鱼优化算法陷入局部最优以后,重新生成种群,并重新执行鲸鱼优化算法。由于在重启的过程中,鲸鱼优化算法可能会找到在前面的重启过程中找到的最优值,为了避免鲸鱼优化算法陷入相同的局部最优,引入三叉树存放在整个过程中搜索到的最优值。主要操作如下: 步骤 1 将鲸鱼优化算法每次迭代找到的最优值存储在三叉树中。当最优值连续n代不变时,重新生成新的种群并重新执行鲸鱼优化算法。 步骤 2 在执行重启机制的过程中,如果生成的最优解在三叉树中存在,判断三叉树中存在的解是不是在本次重启过程中生成的。如果是本次重启过程中生成的,继续执行重启机制,否则执行一次爆炸机制,判断是否可以找到一个更优且未在三叉树中储存的解。如果不能找到一个满足条件的解,本次重启结束,执行下次重启。否则继续执行本次重启操作。 本节提出一种多输出MPRM 电路面积优化方法,该方法使用提出的鲸鱼优化算法搜索对应电路面积最小的最佳极性。方法流程如图2 所示,其实现步骤如下: 图2 方法流程Fig.2 Algorithm flowchart 步骤 2 将生成的最小项存储在2 棵二叉树中,通过基于二叉树的混合极性转换算法转换到0 极性。 步骤 3 设置算法的最大迭代次数Iter,历史迭代次数history_iter=0,种群规模N。 步骤 4 初始化鲸鱼优化算法参数和种群,设置当前迭代次数now_iter=0,记录种群的最优值。 步骤 5 更新鲸鱼算法参数的值。如果L≥0.5则根据式(8)更新位置,如果p<0.5且F<1则根据式(7)更新位置,如果p<0.5且A≥1根据式(9)更新位置[13]。 步骤 6 计算种群的适应度值,确定最优值。 步骤 7 执行爆炸机制,在最优值附近搜索是否还有更优的解。如果存在更优的解,更新最优解的相关信息。再判断最优解是否好于全局最优解,如果好于全局最优解,更新全局最优解的相关信息。 步骤 8如果最优值连续n代没有变化,执行步骤10,否则执行步骤9。 步骤 9now_iter++,history_iter++。如果now_iter 步骤 10history_iter++,如果history_iter 执行重启机制,返回步骤4。否则结束算法,输出全局最优值。 实验的运行环境基于windows10 64 位操作系统,Intel(R) Core(TM) i7-10700 CPU @ 2.90 GHz,32 GB RAM,visual studio community 2019×64。本文实验算法均用C 语言实现。为了充分验证方法的有效性,实验分为以下3 部分:①改进的混合极性转换算法有效性验证。②改进的极性间转换算法有效性验证。③改进的鲸鱼优化算法有效性验证。 改进的鲸鱼优化算法的参数通过引入5 因素4 水平的正交表确定。鲸鱼优化算法、遗传算法(GA)和人工蜂群算法(ABC)的参数通过大量实验获得。为了公平比较各个算法,设置评估次数4 000作为每个算法的结束条件。算法参数设置如表1所示。 表1 算法参数Table 1 Algorithm parameters 为测试改进以后的混合极性转换的效率,选取13 个标准MCNC Benchmark 电路进行测试。进行混合极性转换效率的测试时,将选择电路的最小项转换到0 极性。测试方法为:对每个电路独立运行10 次,统计每次从最小项转换到0 极性的运行时间,取10 次运行时间的平均值。算法1 表示基于列表技术的极性转换算法,算法2 表示基于二叉树的极性转换算法。为了验证算法2 的正确性,执行极性转换算法的同时计算MPRM 表达式的面积。area1 表示通过算法1 进行极性转换得到的面积,area2 表示通过算法2 进行极性转换得到的面积。I/O 分别代表电路的输入位数和输出位数。Rsave表示算法2 比算法1 节省时间的百分比,具体计算公式为 式中:TimeALGO_1为算法1 的平均运行时间;TimeALGO_2为算法2 的平均运行时间。 从表2 可以看出,13 个MCNC Benchmark 电路的area1 和area2 分别保持一致,验证了算法2 的正确性。随着电路输入位数的增多,算法2 执行极性转换所用的时间明显少于算法1,特别对table5、in2、shift、mark1 四个电路的时间节省率达到了99.60%以上。造成以上实验结果的原因可能是用二叉树表达MPRM 电路时生成新项和查找重复项的效率较高。 表2 混合极性转换实验数据Table 2 Experimental data of mixed polarity conversion 在混合极性间转换的过程中,可能会转换到任意极性。极性间的转换采取从极性0 到极性(22···22)3(n位)。所选择的电路和4.1 节中选取的电路一致。算法3 表示基于列表技术的极性间转换算法,算法4 表示基于二叉树的极性间转换算法,Rsave的计算公式和式(10)一致。 从表3 可以看出,对于电路misex1、ex1010,算法3 的运行时间和算法4 相同。对于表中的其他电路,算法3 的运行时间长于算法4 的运行时间。特别是对于电路mark1,算法3 的运行时间达到了15 102.41 s,而算法4 的运行时间只有6.42 s。出现以上实验结果的原因可能受与项个数、去除重复的与项操作、生成新与项操作的影响。 表3 极性间转换实验数据Table 3 Experimental data for conversion between different polarities 为了测试改进的鲸鱼算法的优化效果,选择WOA、GA、ABC 作比较实验。通过式(11)得到节省电路面积百分比: 式中:AVEOTHER_ALGO为WOA、GA、ABC 三个算法在每个电路上运行20 次得到的最优值的平均值;AVEERWOA为ERWOA 算法在每个电路上运行20 次得到的最优值的平均值。从表4 中可以看出,相比于WOA、GA、ABC,EROWA 的标准差为0 的个数达到了8 个。和WOA 相比,ERWOA 的平均电路面积节省为3.45%,最大平均电路面积节省为9.72%。和GA 相比,ERWOA 的平均电路面积节省为5.54%,最大平均电路面积节省为18.32%。相比于ABC,ERWOA 的平均电路面积节省为5.00%,最大平均电路面积节省为14.41%。 表4 算法实验数据Table 4 Experiment data of algorithm 通过以上数据说明,ERWOA 在稳定性和搜索能力方面均优于WOA、GA、ABC。出现上述实验结果的原因可能如下: 1)WOA、GA、ABC 容易陷入局部最优解且不容易跳出。因为ERWOA 引入了重启机制,所以可以有效跳出局部最优解,从而增强了算法的稳定性。 2)WOA、GA、ABC 搜索精度比ERWOA 低。因为ERWOA 引入了爆炸机制,所以可以在有限的迭代次数内搜索到更优解。 为了进一步说明ERWOA 算法的性能,选择4 个测试电路绘制收敛曲线。其中,横坐标代表算法前30 次的迭代次数,纵坐标代表算法运行20 次找到的面积的平均值。 从图3~图6 中可以看出,和WOA、GA、ABC三种算法相比,ERWOA 在收敛速度、找到最优值方面效果较好。 图3 newcond 电路收敛曲线Fig.3 Convergence curves of newcond circuit 图4 misex3 电路收敛曲线Fig.4 Convergence curves of misex3 circuit 图5 in0 收敛曲线Fig.5 Convergence curves of in0 circuit 图6 b2 电路收敛曲线Fig.6 Convergence curves of b2 circuit 本文提出一种基于爆炸机制和重启机制的鲸鱼优化算法用于求解基于MPRM 电路的面积优化问题,主要结论如下: 1)提出一种基于二叉树的极性转换算法。和基于列表技术的混合极性转换算法相比,转换效率最高提升99.93%,和基于列表技术的极性间转换算法相比,转换效率最高提升99.96%。 2)多输出MPRM 电路面积优化方法与GA 算法相比,节省的电路面积百分比最高为18.32%,平均为5.54%;与ABC 算法相比,节省电路面积百分比最高为14.41%,平均为5.00%;与WOA 相比,最大电路面积节省为9.72%,平均为3.45%。2 快速多输出MPRM 电路极性转换算法
2.1 快速混合极性转换算法
2.2 快速极性间转换算法
3 多输出MPRM 电路面积优化
3.1 鲸鱼优化算法

3.2 爆炸机制
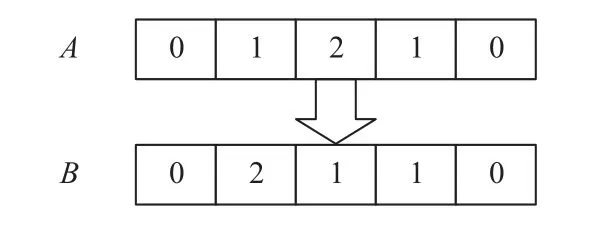
3.3 重启机制
3.4 多输出MPRM 电路面积优化方法

4 实验结果及分析

4.1 混合极性转换算法验证
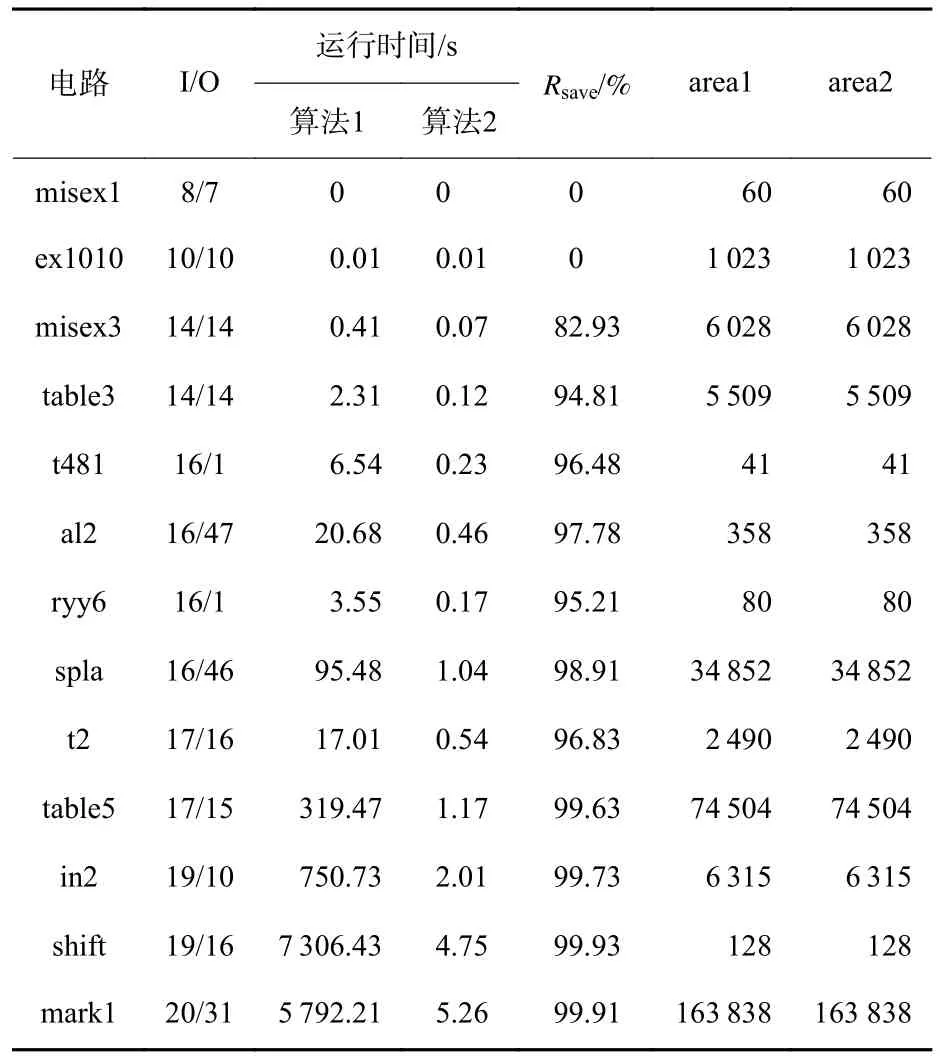
4.2 极性间转换算法验证
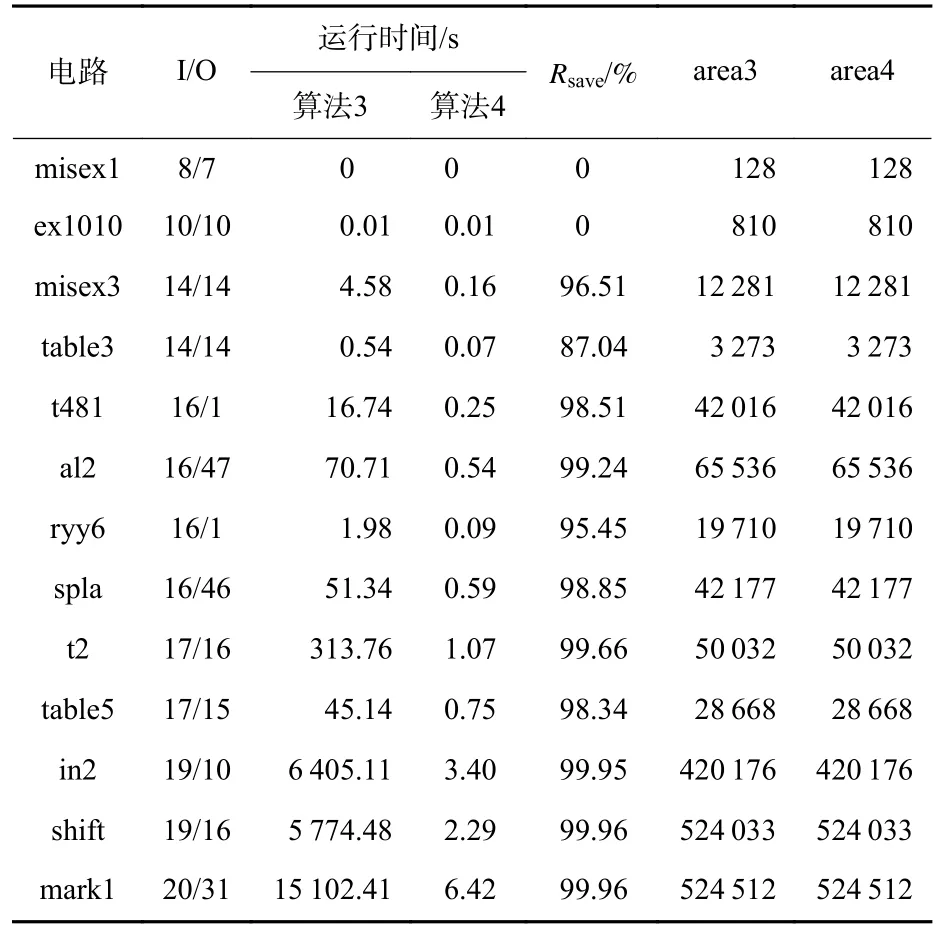
4.3 多输出MPRM 电路面积优化效果验证
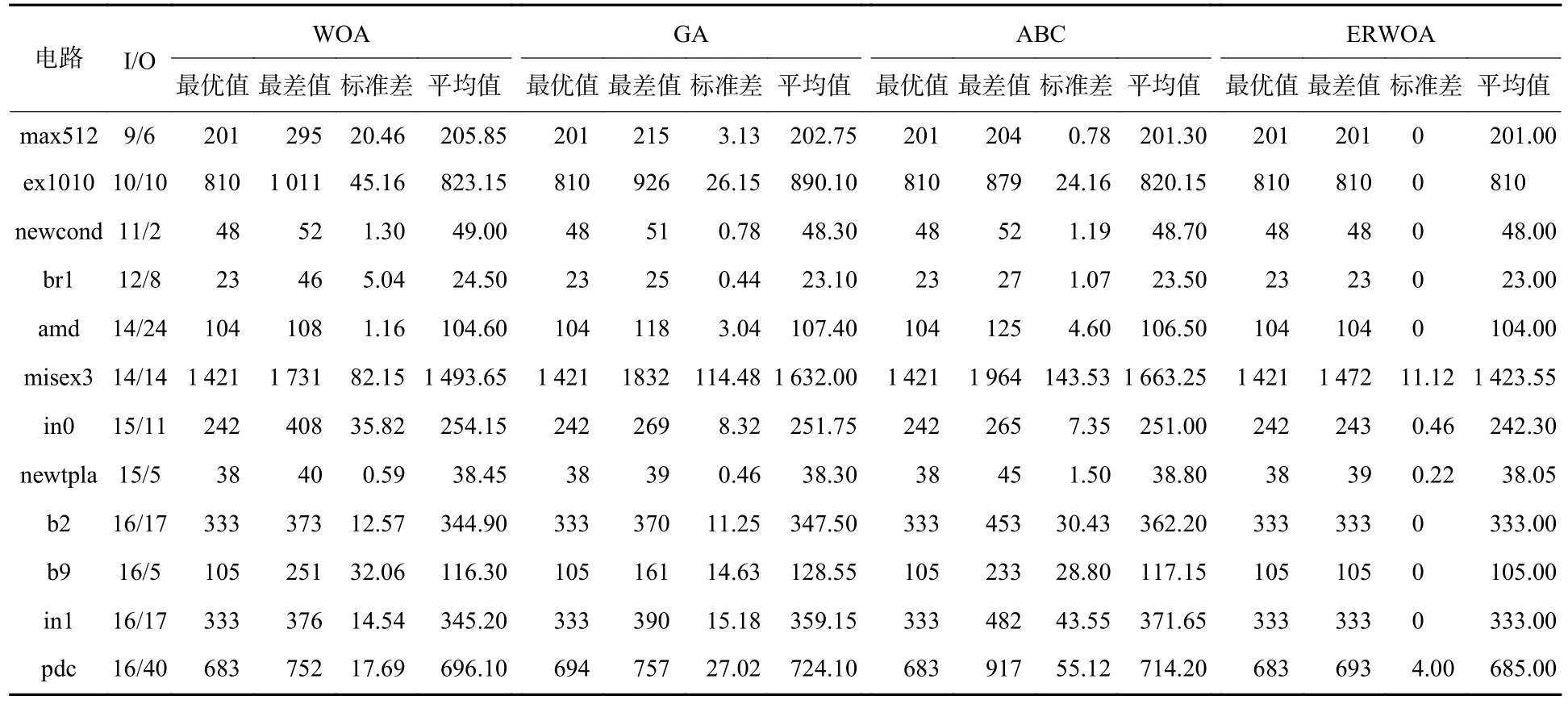
4.4 收敛性对比
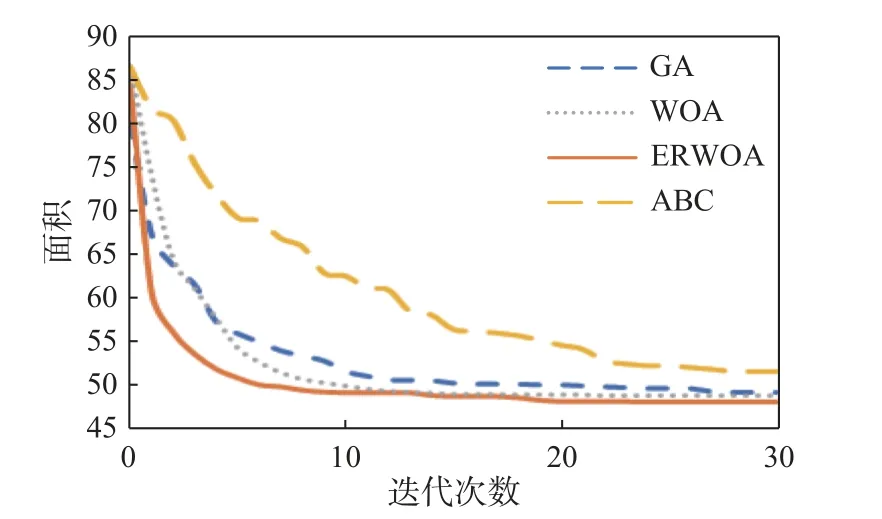
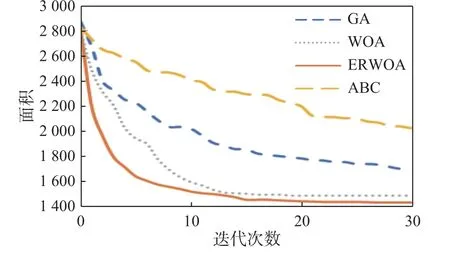
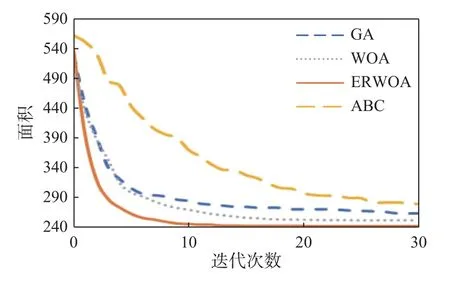
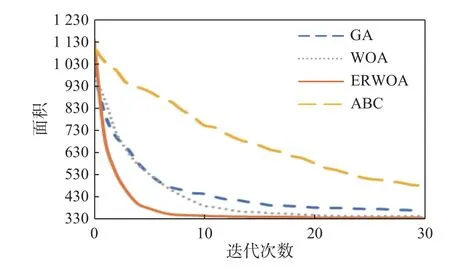
5 结 论

