基于ADRC 的电传动飞机牵引车控制系统设计

张军，文川，阳星，张新荣，贾永乐

(1.长安大学 公路养护装备国家工程实验室，西安 710064；2.长安大学 道路施工技术与装备教育部重点实验室，西安 710064；3.西安睿诺航空装备有限公司，西安 710060)

飞机牵引车是用于机场地面牵引飞机移动的地面特种车辆，包括有杆和无杆牵引车2 类[1-2]。有杆牵引车的牵引杆一端连在飞机前起落架上，另一端连在牵引车上，存在半径过大的问题，减少了停机坪内最大容纳飞机的数量；而无杆牵引车采用一套抱紧提升机构把飞机前起落架夹持住，将前起落架驮载在牵引车上行驶，具有转向灵活和转弯半径小的特点[3]，可在相同空间拖放更多飞机。现有的牵引车多为液压传动，具有牵引力矩大、启停平稳的优点，但是电传动方式具有绿色环保特点，将逐步成为主流产品。由于飞机惯性大，行驶过程中所需的牵引力矩变化大，如何提高电传动牵引车的牵引稳定性成为研究热点。

关于飞机牵引车稳定性的研究较少，本文以相关运动平台稳定性进行分析。魏延辉等[4]针对水下机器人稳定性易受海流影响的问题，采用自适应补偿的方法设计了自适应控制器，并进行多方向运动稳定性控制试验，提高了水下机器人的运动稳定性。俞建成等[5]针对水下机器人稳定性差的问题，采用模糊神经网络的方法设计控制器，发现该控制器提高了水下机器人稳定性。魏静波等[6]为提高卫星姿态运动的稳定性，采用自适应滑模变结构的控制方法，设计了姿态三轴稳定控制器，仿真发现该控制方法对提高卫星姿态运动的稳定性是有效的。殷春武和刘素兵[7]针对航天器在轨捕获目标过程中姿态快速稳定要求，采用反演和滑模控制的方法，设计了一种鲁棒姿态控制器，仿真验证了该控制器的快速稳定性和强鲁棒性。马龙等[8]针对高速运动状态下外界扰动和系统抖振会影响球形机器人运行，采用分层滑模控制方法，设计了自适应评估和补偿控制器，实验发现该控制方法能够有效提高系统稳定性和鲁棒性。Dumlu[9]采用分数阶自适应积分滑模控制方法进行六自由度机械手的轨迹跟踪控制，与经典积分滑模控制相比，该控制器具有很好的轨迹跟踪响应特性和稳定性。Yue 等[10]为改善球形机器人固有振动使控制性能恶化的问题，采用一种基于扩展状态观察器的自适应分层滑模控制方法，设计了一种扩展的状态观测器，仿真发现设计的球形机器人闭环控制系统具有强大的自适应能力和良好的稳定性。以上研究表明，良好的控制方法可提高运动平台的稳定性，但现有的研究对象都是基于轻型设备，难以为负载较重的电传动飞机牵引车提供参考，缺乏专门针对电传动牵引特性分析及其控制策略的研究。

由于飞机大惯性和牵引地面不平整的原因，电传动飞机牵引车在实际运行中存在较多不可预测的因素，增加了控制系统的扰动，传统的PID 控制算法难以解决牵引车系统扰动性问题[11]。李锦英等[12]针对运动平台上光电跟踪系统应有强的抗扰动性能需求，采用自抗扰控制（active disturbance rejection control，ADRC）的方法，设计了稳定平台的自抗扰控制器，实验发现，与采用PI 控制相比，自抗扰控制器的稳定跟踪能力和扰动抑制能力都有一定的提高。孙明玮等[13]为改善风载荷干扰对深空探测天线跟踪精度和寿命的影响，采用ADRC 方法设计了位置环线性自抗扰控制器，实验发现，设计的自抗扰控制器提高了系统抗风干扰的能力。朱进权等[14]针对高速磁悬浮列车负载在换步过程中变化剧烈的问题，采用ADRC 和负载功率前馈的控制方法，设计了高速磁悬浮列车控制器，提高了列车的抗负载扰动能力和系统动态稳定性。周新力和李醒飞[15]针对光电跟踪系统存在的时变摩擦力、外界扰动等非线性因素引起的控制精度降低问题，采用积分反步自抗扰控制方法，有效抑制时变摩擦及外界扰动，实现了光电跟踪系统的高精度位置控制与快速动态响应。姚芳等[16]针对汽车防抱死制动系统存在非线性、时变性及参数不确定性等问题，采用ADRC方法设计了基于滑移率的二阶非线性自抗扰控制器，仿真和实验发现，相比PID 控制器防抱死制动系统，二阶非线性自抗扰控制器防抱死制动系统的稳定性更好。现有研究表明，自抗扰技术能较好地提高系统稳定性，为飞机牵引车稳定性控制提供参考，以减少大惯性飞机带来的转矩扰动。

针对飞机牵引过程的时变摩擦力及飞机的大惯性扰动引起平稳性低的问题，本文根据飞机牵引运动的数学模型建立了牵引车的动力学模型，分别采用ADRC 和PID 算法设计牵引车控制器，仿真对比牵引车变速行驶过程中的稳定性和抗扰能力，并通过实车试验验证仿真模型及结果的正确性和ADRC的优越性，为高稳定性的牵引车研发提供依据。

1 飞机牵引车数学建模

1.1 运动学建模

根据飞机牵引车的运动特征，通过牵引系统的转向对整车动力学进行建模分析。图1 为飞机牵引车运动分析。在笛卡儿直角坐标系xOy中，定义了牵引车后轴中心M1，飞机后轴中心M2，飞机转动中心O1，牵引车转动中心O2，牵引车体的转向角β，牵引车和飞机的夹角θ，飞机的转向角λ，牵引车前轮转向角α。

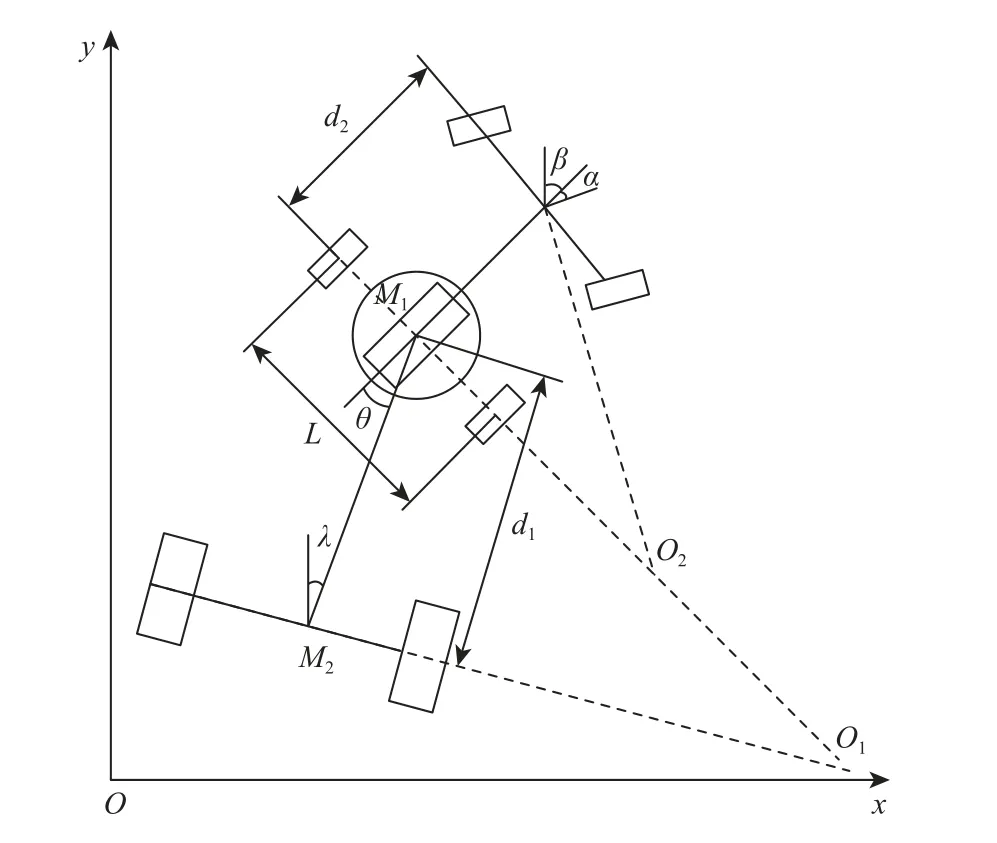
图1 飞机牵引车运动学分析示意图Fig.1 Schematic diagram of kinematic analysis of aircraft tug

由图1 可知，电传动飞机牵引车的系统运动学方程可表示为

式中：x、y为牵引车后轴中点M1的坐标；v为牵引车后轴中点M1的速度；d1为飞机轴距；d2为牵引车轴距。

式(1)可用矩阵表示为

定义Fxi、Fyi(i=1,2)为路面通过各轮胎沿坐标轴方向加在牵引车上的力。牵引车在水平面内的动力学方程可表示为

式中：i为驱动车轮编号(i=1,2)；M为牵引车总质量；Ff为轮胎滚动阻力，计算式为

其中：V(C)long为轮胎中心向前的速度；Cf为滚动阻力系数；Fnorm为正向力。

Fyi=0，则Fxi可由式（6）计算：

式中：Jxi为各驱动轮的转动惯量；TL′为负载轴上的驱动转矩；r为驱动轮半径。

1.2 电机系统建模

牵引车电机选用永磁同步电机，并假设永磁同步电机满足以下条件：①忽略永磁同步电机铁芯的饱和；②不计永磁同步电机中的涡流和磁滞损耗。

永磁同步电机在转子磁场定向d、q坐标系中的状态方程为

式中：ud、uq分别为定子电压矢量的d、q分量；id、iq分别为定子电流矢量的d、q分量；L为定子电感；RS为定子电阻；Pn为极对数；ω为转子机械角速度；ψf为永磁磁链；TL为负载转矩；B为黏滞摩擦系数；J为电机和负载的转动惯量。

将电机的机械运动方程改写为

2 飞机牵引车自抗扰控制器设计

ADRC 技术发扬了经典PID 控制技术的精髓，设计不依赖于对象的数学模型，不会区分系统的内扰和外扰，而是直接观测补偿系统的总扰动，适用于内外扰动共存的飞机牵引系统控制。飞机牵引系统速度控制器根据转速实测值n对当前控制给定值n∗的偏差驱动调节电流控制器参考值i∗，进而与实测电流i相差调节电机转速，控制飞机牵引车的运动。为提高飞机牵引的稳定性，设计基于转速和电流的自抗扰控制器，并将其植入到飞机牵引控制系统，最终得到如图2 所示的基于自抗扰控制器的飞机牵引车结构。

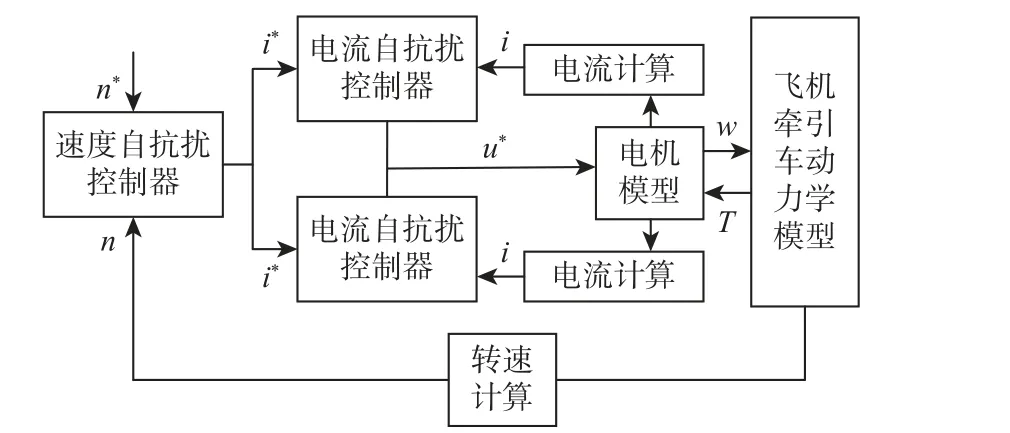
图2 基于自抗扰控制器的飞机牵引车结构Fig.2 Aircraft tug structure based on active disturbance rejection controller

2.1 飞机牵引车自抗扰转速控制系统设计

图3 为ADRC 的原理结构，包括跟踪微分器(tracking-differentiator, TD)、扩张状态观测器(extended state observer, ESO)和状态误差反馈控制率(nonlinear states error feed-back, NLSEF)。图3 中：u0和u分别为误差反馈的控制信号和经过扰动补偿后的控制信号；y∗和y分别为期待输出的信号和实际输出的信号；z11为y∗的微分跟踪值；z21和z22分别为扰动信号的观测值和输出值。转速TD 通过数值计算使TD 输出的转速n∗快速跟踪其期望的信号n，并提取其微分信号n˙，通过配置TD 的速度因子 ρ、函数幂指数α0和区间宽度 σ0，控制跟踪过程的过渡时间和跟踪效果。转速n的跟踪方程为

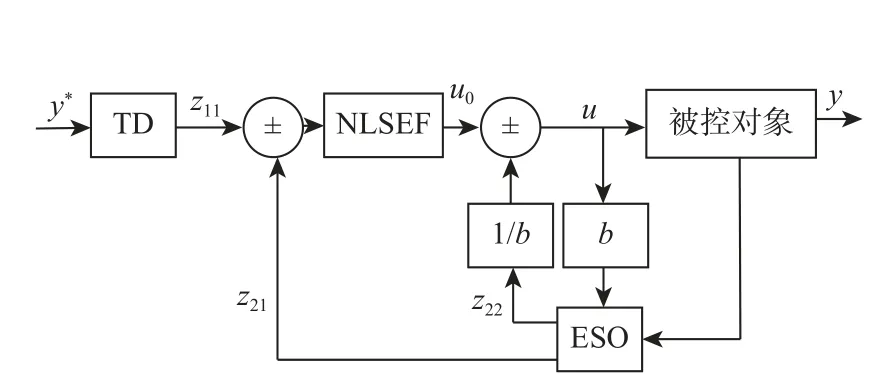
图3 ADRC 原理结构Fig.3 Principle structure of ADRC

式中：f al(e,α,σ)定义为

其中：n∗为 期望输出的转速信号；n11为n∗的跟踪信号。

为使转速ESO 的状态变量跟踪系统的状态变量，结合式（7），设计的转速ESO 如下：

式中：un为经过扰动补偿后的速度控制信号；n21、n22为速度扰动信号观测值；β01、β02为转速ESO 的增益。

转速ESO 实时得到总扰动f(ω,TL)的估计值，如果在控制率中予以补偿，则可实现主动扰动的功能。为此，设置控制量的NLSEF 方程为

式中：kp为速度NLSEF 的增益；n22/b为用于补偿速度内外扰的补偿量；un0为速度误差反馈的控制信号。

2.2 飞机牵引车自抗扰电流控制系统设计

电流TD 通过数值计算使TD 输出的电流i快速跟踪其期望的电流信号i∗，并提取其微分信号˙i，通过配置TD 的速度因子 ρ、函数幂指数α0和区间宽度σ0，控制跟踪过程的过渡时间和跟踪效果。电流i的跟踪方程为

式 中：i∗为 速 度 环 得 到 的 控 制 信 号；i11为i∗的 跟 踪信号。

为使电流ESO 的状态变量跟踪系统的状态变量，结合式(9)，设计的电流ESO 如下：

根据式(9)可知

式中：ui为经过扰动补偿后的电流控制信号；i21、i22为电流扰动信号的观测值；L为电机电感。

电流ESO 实时得到总扰动 ωq(t)的估计值，如果在控制率中予以补偿，则可实现主动扰动的功能。为此，设置控制量的NLSEF 方程为

式中：β1为 电流NLSEF 的增益；(i22+g(i21))/b为补偿电流内外扰的补偿量；ui0为电流误差反馈的控制信号。

3 飞机牵引车仿真及结果分析

考虑到飞机的贵重性，难以采用物理飞机试验，通过仿真模型可避免意外，缩短样机调试周期。为此，以影响飞机牵引稳定的变量转速和转矩为研究对象，在ADAMS 中建立动力学模型，在MATLAB/Simulink 中建立控制系统模型，通过模型联合方法建立电传动飞机牵引车联合仿真模型，可形成如图4所示的ADAMS 与MATLAB 联合仿真原理。

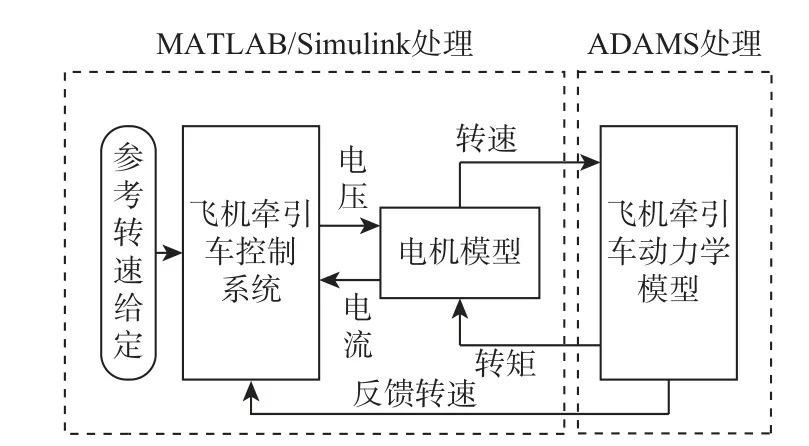
图4 ADAMS 与MATLAB/Simulink 联合仿真原理Fig.4 Co-simulation model of ADAMS and MATLAB/Simulink

联合仿真包括控制系统、电机模型和动力学模型3 部分，工作原理如下：①输入转速信号，经控制系统转化为电压信号，带动电机以输入的转速运转；②电机轴转速信号传递给ADMAS 动力学模型负载轴，牵引车运动，同时将反馈负载轴转速和转矩传递给电机轴；③电机轴转速和转矩反馈到MATLAB/Simulink 控制系统，从而形成一个闭合的控制回路。

3.1 飞机牵引车动力学仿真建模

将设计的10 t 飞机牵引车导入ADMAS，构建飞机牵引车动力学模型，得到如图5 所示的电传动无杆飞机牵引车动力学模型。

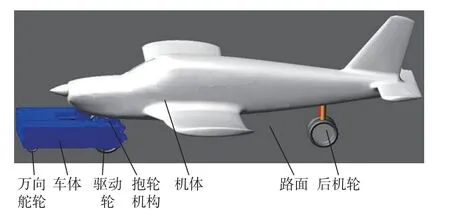
图5 电传动无杆飞机牵引车动力学模型Fig.5 Dynamic model of electric rodless aircraft tug

从图5 可知，电传动无杆飞机牵引车动力学模型主要包括车体、机体、后机轮、驱动轮、万向舵轮、路面、抱轮机构。电传动无杆飞机牵引车元件约束关系如表1 所示，飞机和牵引车参数输入数据如表2 所示。

表1 电传动无杆飞机牵引车元件约束关系Table 1 Elemental constraints of electric rodless aircraft tug

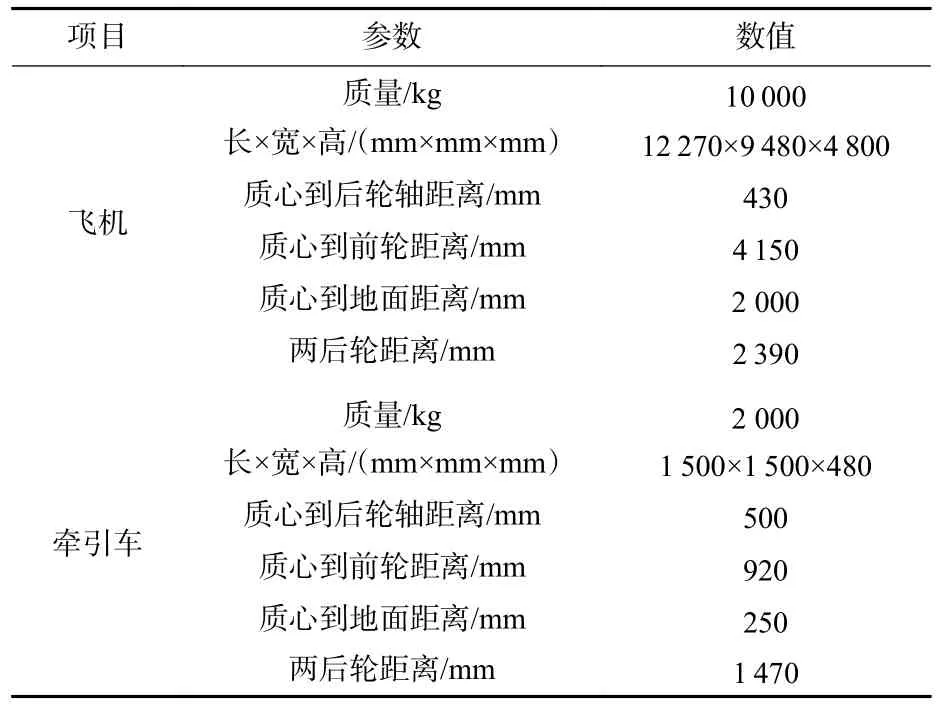
表2 飞机和牵引车参数输入数据Table 2 Input parameters of aircraft and tug

3.2 飞机牵引车控制系统仿真建模

为实现牵引车的控制性能，分别设计了基于PID 和ADRC 的控制算法，并在MATLAB/Simulink构建了电传动飞机牵引车控制系统的仿真模型，如图6 和图7 所示。图中：设定转速为牵引车运行的速度，通常根据实际需要由人为指定，输出参考转速n∗；速度PI 控制器和速度自抗扰控制器是牵引车速度控制算法，控制牵引车速度以给定转速运行，其中，速度自抗扰控制器是速度PI 控制器基础上的改进算法；电流PI 控制器和电流自抗扰控制器是牵引车电机电流控制算法，控制牵引车电机电流恒定，以减少牵引车转矩波动带来的电流扰动，其中，电流自抗扰控制器是电流PI 控制器基础上的改进算法；电机模型是牵引车电机数学模型；飞机牵引车动力学模型由3.1 节建立的ADAMS 动力学模型转换得到；电流计算和转速计算是等效换算电流和转速，使其电机输出电流换算为矢量控制电流、电机输出角度形式转速(单位为rad/s)换算为转数转速(单位为r/min)。

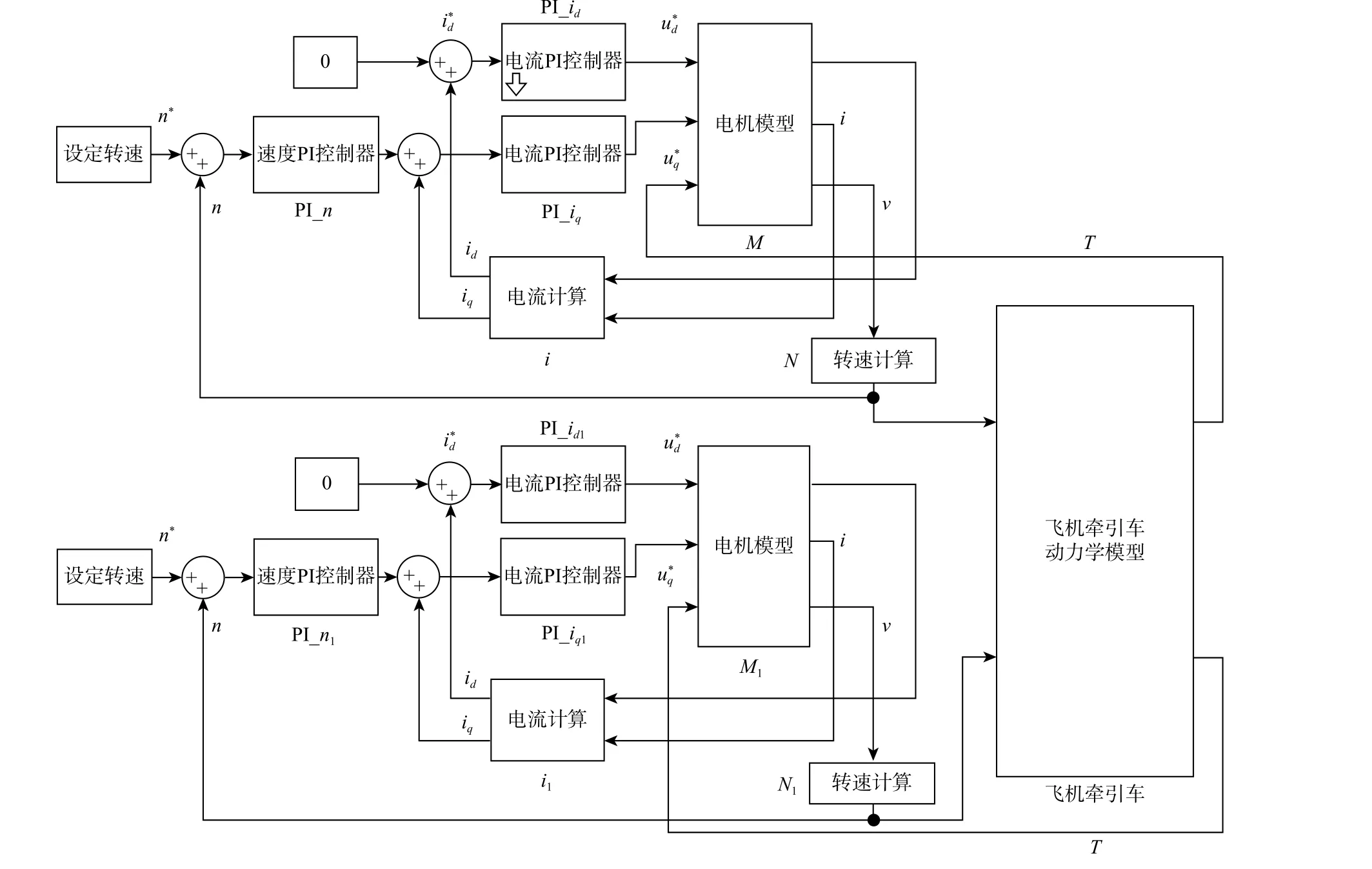
图6 PID 飞机牵引车联合仿真模型Fig.6 Co-simulation model of PID aircraft tug

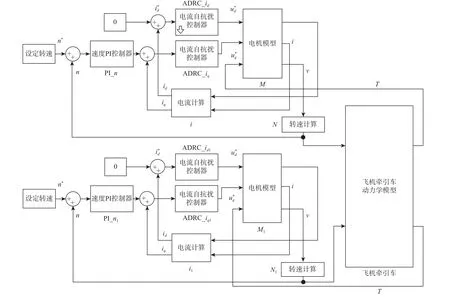
图7 ADRC 飞机牵引车联合仿真模型Fig.7 Co-simulation model of ADRC aircraft tug

3.3 飞机牵引车仿真结果分析

3.3.1 仿真条件设定

仿真时间7 s,采样间隔0.01 s,电机转速分别设定为0, 200, 650 r/min，电传动无杆飞机牵引车仿真和试验条件具体设置如表3 所示。

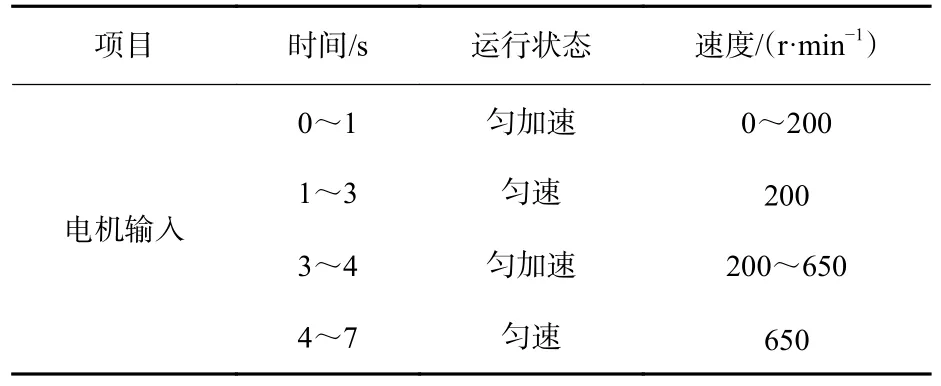
表3 电传动无杆飞机牵引车仿真和试验条件Table 3 Simulation and experimental conditions of electric rodless aircraft tug

表3 中，0～1 s 为仿真飞机牵引车第1 加速阶段，电机轴转速由0 升至200 r/min；1～3 s 为仿真飞机牵引车第1 匀速阶段，电机轴转速保持200 r/min；3～4 s 为仿真飞机牵引车第2 加速阶段，电机轴转速由200 r/min 升至650 r/min；4～6 s 为仿真飞机牵引车第2 匀速阶段，电机轴转速保持650 r/min。

3.3.2 仿真结果分析

1）PID 控制结果

采用仿真法不断调试速度环和转矩环的PI 控制参数，以较优结果的参数来构建控制系统。仿真分为加速阶段、匀速阶段和减速阶段，以电机输出端转速结果为例进行展示，如图8 所示。

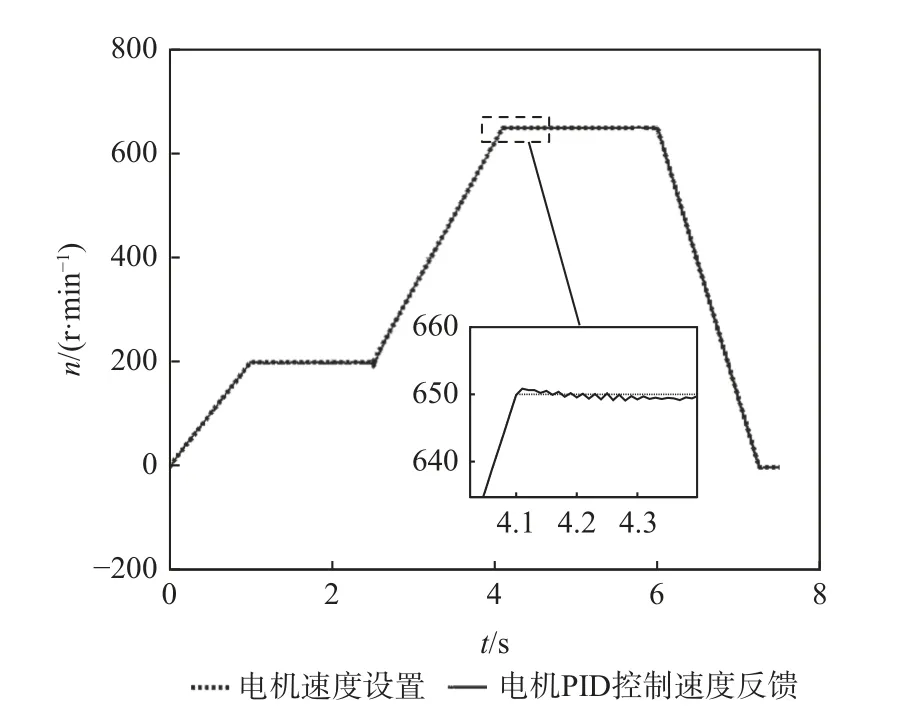
图8 PID 仿真电机轴转速特性曲线Fig.8 Motor shaft speed characteristic curves of PID method

在速度较高的第2 匀速阶段，电机轴的反馈转速有一定的振动现象。由此得出结论，采用PID 控制时，飞机牵引车在高转速时有一定速度波动，需要对控制系统进一步优化。

最终获得的PID 控制的转速环和电流环的仿真参数如表4 所示，由于仿真与试验环境的差异，仿真参数和实际试验参数也不一样。样机试验中，PID 试验参数调试取值范围为仿真参数±10%，得到样机参数的调试范围，为提升牵引车控制性能和移植复杂算法到自制的牵引车样机奠定基础。

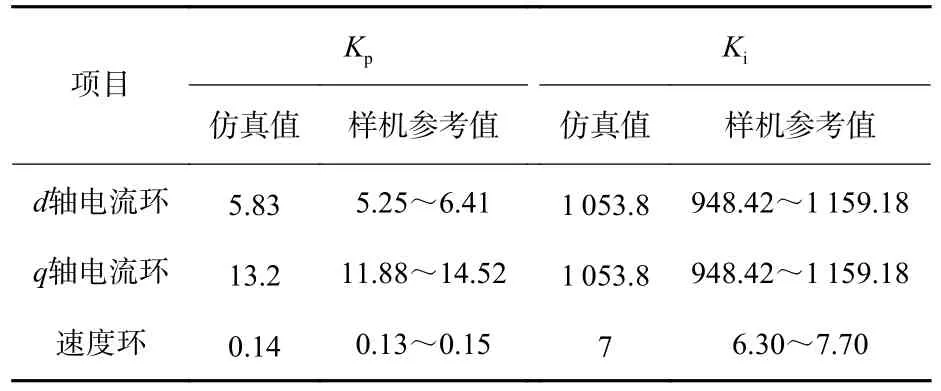
表4 电传动无杆飞机牵引车PID 试验参数Table 4 PID parameters of electric rodless aircraft tug

2）ADRC 控制结果

由于大惯性飞机和不平整路面的影响，当电机的负载扰动较大，PID 控制算法的速度波动较大，难以满足稳定性要求。开展ADRC 算法优化PID控制，不断调试速度环和转矩环的ADRC 控制参数，选取得到控制性能较好的电机轴转速特性曲线，如图9 所示。

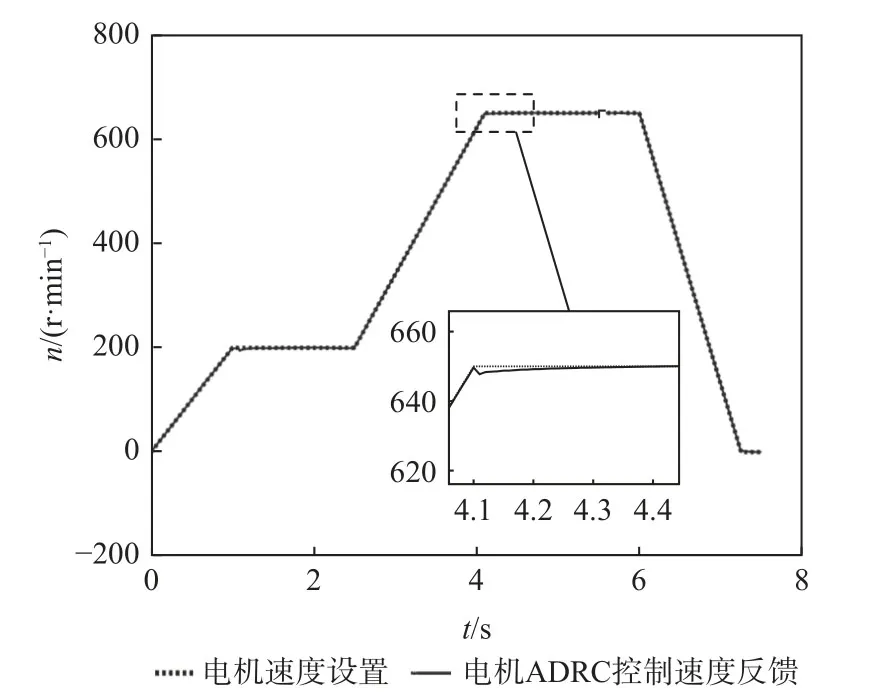
图9 ADRC 仿真电机轴转速特性曲线Fig.9 Motor shaft speed characteristic curves of ADRC method

整个阶段电机轴反馈转速中无波动现象。与PID 控制导致的波动相比，改进ADRC 控制明显提高了飞机牵引车的稳定性。

试验获得的ADRC 控制的转速环和电流环的仿真参数如表5 所示，样机试验将以ADRC 仿真试验参数±10%作为调试取值范围。

表5 电传动无杆飞机牵引车ADRC 试验参数Table 5 ADRC parameters of electric rodless aircraft tug

4 飞机牵引车样机控制试验

4.1 样机试验验证方案

为解决真实飞机拖载试验问题，根据最大10 t飞机的载荷分配，自制了模拟加载平台，如图10所示。其加载原理为：根据10 t 飞机的重心位置，进行力的分解与计算，可得出飞机前轮受力1 t，飞机后轮受力9 t，且飞机前轮将其受力直接施加在牵引车抱轮机架上，飞机后轮则将其受力直接施加与地面。

图10 电传动飞机牵引车样机试验平台Fig.10 Experiment platform of electric aircraft tug prototype

由图10 可知，飞机前轮的受力等效于1 t 质量铁块加载于牵引车抱轮机架，飞机后轮的受力等效于9 t 质量铁块加载于地面且可被牵引车进行拖拽牵引。

4.2 样机组成

根据电传动无杆飞机牵引车机构模型和控制模型，搭建样机试验平台，实现牵引车稳定性控制。搭建的电传动无杆飞机牵引车的样机试验平台由参数监控设备、控制面板、传动机构、抱轮机构、摇杆控制手柄及模拟负载刚体组成，如图11所示。

图11 电传动飞机牵引车样机试验平台Fig.11 Electric aircraft tug prototype experiment platform

摇杆控制手柄作为操作人员运动需求发出信号的元件，通过无线通信对飞机牵引车的控制器发出指令。操作人员可通过摇杆控制手柄遥控飞机牵引车的抱轮动作及行走运动，具有无极变速灵活方便的优点。参数监控设备作为设计人员调试设备时需要观察的运行参数，用于后续分析，包括电机转矩和转速。传动机构作为整个控制系统的动力来源，由电机、减速机和车轮组成。其中，电机选用3.1 kW 的永磁同步电机，减速机选用减速比51 的行星减速轮TTRA-165E。抱轮机构对飞机前轮进行固定，由液压缸、液压管道、上压板、后挡板及前挡板组成。液压泵压缩液压油，通过液压管输送至液压缸带动上压板、后挡板及前挡板执行相应的抱轮动作。

4.3 控制稳定性试验

1）PID 控制结果

基于联合仿真模型，将PID 算法移植至飞机牵引车样机系统，进行电传动飞机牵引车的稳定性分析。试验条件与仿真条件保持一致，调试获得牵引车电机轴转速特性曲线如图12 所示。

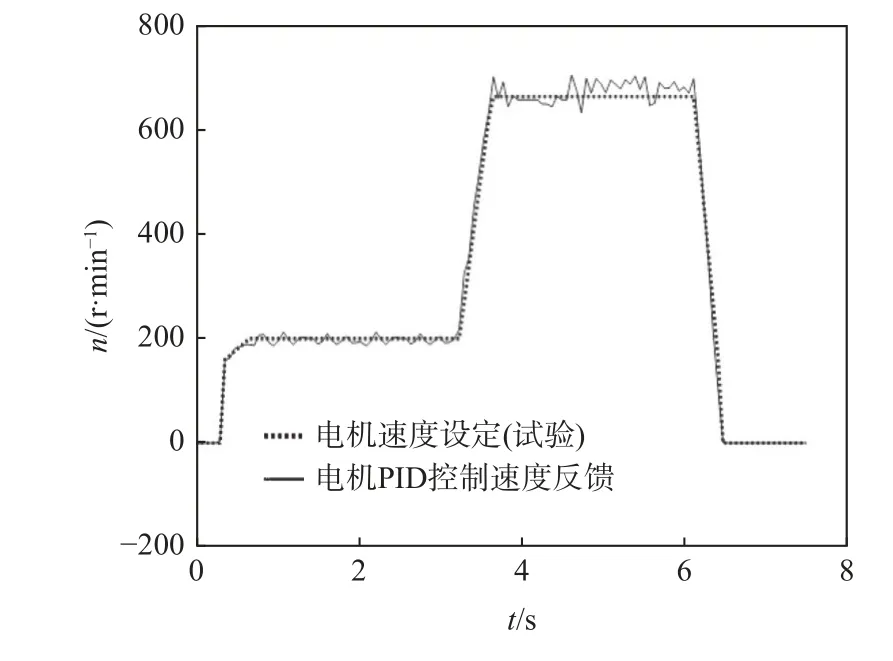
图12 电机轴转速特性曲线（PID 试验）Fig.12 Motor shaft speed characteristic curves(PID experiment)

由图12 可知，在给定的设定转速下，实际转速具有较大的波动，尤其是在3.5～6 s 转速较高的工况下，实际转速波动更为明显，达到±50 r/min，严重影响牵引作业的稳定性。试验用的PID 参数是通过仿真得到，这也验证了仿真模型及其结果的正确性。但值得注意的是，由于试验中的环境相对仿真更为复杂，且是仿真难以模拟的，如打滑、载荷分布不均和路面平整度参差不齐等，试验中的转速波动比仿真更大，平稳性更差。

2）ADRC 控制试验

基于联合仿真模型，将ADRC 算法移植至飞机牵引车样机系统，进行电传动飞机牵引车的稳定性分析。试验条件与仿真条件保持一致，调试获得牵引车电机轴转速特性曲线如图13 所示。

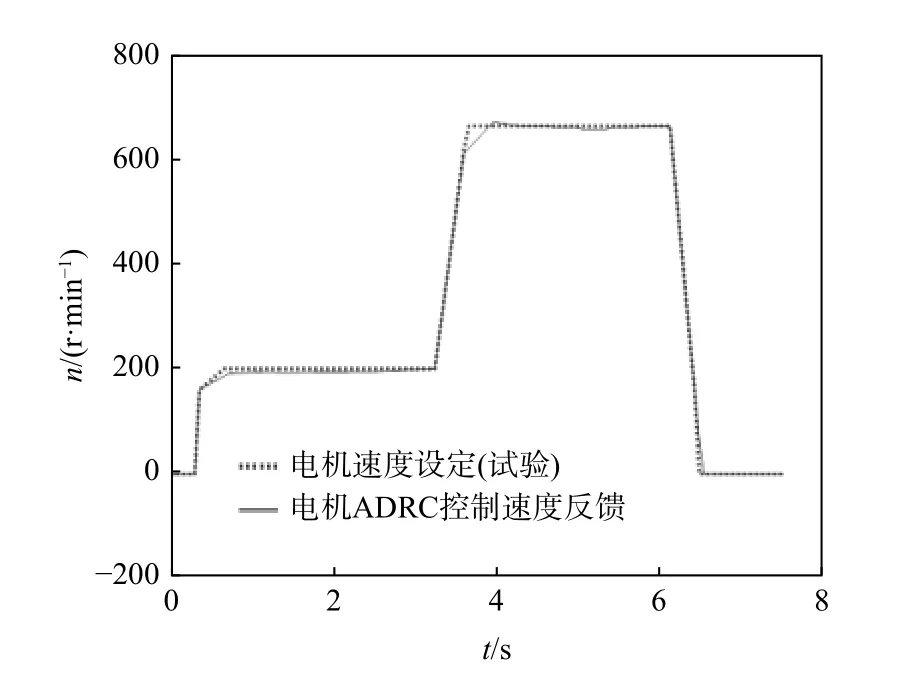
图13 电机轴转速特性曲线（ADRC 试验）Fig.13 Motor shaft speed characteristic curves(ADRC experiment)

由图13 可知，在ADRC 算法的优化下，转速具有良好的跟踪响应特性，整个工况的实际转速波动较小，提高了飞机牵引车的稳定性。此ADRC 试验算法和参数通过仿真得到，同时也验证了仿真的正确性。

3）优化前后对比

综上，基于仿真PID 控制参数和ADRC 控制参数，将其仿真模型移植到样机试验控制系统中，进行电传动飞机牵引车控制系统设计，均提高了飞机牵引运动的稳定性，验证了仿真模型的正确性和有效性。

为进一步量化稳定性优化效果，引入如下不稳定性衡量指标：

式中：nmax为匀速过程中的速度最大值，r/min；nmin为匀速过程中速度最小值，r/min；n为匀速的稳定速度值，r/min。

将图12 和图13 的转速特性曲线数据导出，可观察并计算到如表6 所示的不稳定性值。

表6 电传动无杆飞机牵引车试验数据Table 6 Experimental data analysis of electric rodless aircraft tug

由表6 可知，在1～3 s 的匀速运动过程中，ADRC 控制的不稳定性为4.4%，PID 控制的不稳定性为13.5%；在3～7 s 的匀速运动过程中，ADRC 控制的不稳定性为2.1%，PID 控制的不稳定性为11.0%。显然，在1～3 s 的匀速运动过程中，ADRC 控制的稳定性相对PID 控制的稳定性提升了9.1%；在3～7 s 的匀速运动过程中，ADRC 控制的稳定性相对PID 控制的稳定性提升了8.9%，进一步验证了采用ADRC 算法的有效性。

5 结 论

1）为解决牵引车平稳性问题，以10 t 飞机为对象，构建了基于ADAMS 和MATLAB/Simulink 的飞机牵引车联合仿真模型，并得到仿真的控制参数，为提升牵引车控制性能和移植复杂算法到自制的飞机牵引车样机奠定基础。

2）采用传统PID 算方法可实现飞机牵引车的牵引功能，但在粗糙地面存在驱动电机转速波动问题，影响牵引车的平稳性。

3）采用ADRC 算法优化PID 算法，提高了飞机牵引车的稳定性。

4）采用联合仿真获得飞机牵引车的结构参数和控制参数，减少了直接实物调试过程中出现危险牵引工况，并为实物控制系统的研发和样机试验提供理论依据。