似然函数视角下小企业信用风险最优评价指标体系的建立
白雪鹏, 赵志冲
(东北财经大学 管理科学与工程学院,辽宁 大连 116025)
0 引言
信用风险是商业银行面临的主要风险,在国民经济中具有重要影响。例如2008年金融危机,正是由于次级贷款大规模违约引起的。2021年底中国商业银行的不良贷款余额高达3万亿元,该领域的信用风险管理问题亟待解决。
小企业在国民经济中占有重要地位,但却存在融资难、融资贵的现象。小企业融资的85%以上来自于商业银行,但是银行为小企业发放的贷款占比不足30%。2019年两会的报告中提出“今年商业银行小企业贷款要增长30%以上”的要求。对商业银行而言,既要响应国家政策要求,加大小企业贷款发放力度,又要合理控制小企业贷款风险问题。因此,亟需一套合理的评价小企业的信用风险的体系。建立小企业信用评价指标体系是评价贷款小企业信用风险的前提和基础,它是由若干个信用评价指标构成的一个整体。如果信用评价指标体系不合理,更谈不上合理评价小企业的违约风险,会对银行贷款决策产生误导,造成银行损失[1]。建立合理的信用评价指标体系至少涉及到以下两个问题。一是哪一些指标可以作为信用评价指标。一个指标能否用于信用评价的本质是这个指标对判别小企业违约还是不违约具有一定的区分能力,即指标具有违约判别能力。在银行实际操作和学术研究中,用于信用评价的指标举不胜举,但是这些指标是否都具有违约鉴别能力。如何在众多的指标中,遴选出具有违约鉴别能力的指标是建立信用评价指标体系的基础。二是不同信用评价指标如何构成一个最优的信用评价指标体系。指标的不同组合方式可以构成不同的指标体系,n个指标可以构成2n-1种指标体系,如何在众多的指标体系中,遴选出一个最优的指标体系。与单个信用评价指标的遴选标准一致,最优指标体系的判别标准就是这个体系具有最强的违约判别能力。
信用评价指标选取的关键在于指标能够有效判别小企业是否违约、即指标具有违约判别能力;指标体系的构建亦然,即最优的指标体系具有最强的违约判别能力。本文首次提出了通过对数似然函数值来衡量指标及指标体系违约判别能力这一新的标准。进一步以指标体系的对数似然函数值最大为目标函数,构建0-1整数规划,通过遗传算法求解出违约鉴别能力最大的小企业信用风险评价指标体系。
1 文献综述
小企业信用评价指标体系的构建方面的研究已经取得了长足的进展,此类研究主要有四种角度:
一是通过定性方法识别哪些指标能够用于信用评价。例如5C评价标准,就是从道德、资本、能力、保证和环境5个角度遴选指标构成信用评价体系[2]。
二是通过指标数据信息、不考虑指标对违约状态的区分能力遴选指标。熊志斌基于SVM筛选影响澳大利亚个人信用的关键特征[3]。马晓君基于信息熵筛选影响信用风险的指标[4]。BENNASAR等通过联合互信息最大的方法遴选指标[5]。WEI等通过挖掘财务报表的文本风险识别风险因素[6]。YAO等通过添加指标后体系依赖度的变化量衡量指标的重要程度[7]。WANG等通过F得分等三种过滤方法对指标进行了筛选[8]。WANG等通过条件熵来剔除冗余指标[8]。
三是定量识别单一指标是否有效。例如迟国泰分别通过构建wald统计量[10]、F统计量[11]、格朗日统计量[12]等方法删除不能显著区分小企业违约状态的指标。孟斌通过方差齐性检验确定某一个指标是否有效[13]。潘明道通过Fisher判别的方法确定有、无某一指标时指标体系的判别精度变化反应该指标的违约判别能力[14]。赵志冲通过似然比检验的方法确定指标的违约判别能力[15]。
四是通过定量方法识别指标体系的违约鉴别能力。例如MALDONADO等在考虑指标获取成本的基础上通过支持向量机模型构建信用评价指标体系[16]。NIKOLIC等通过强力逻辑回归模型在5个指标构成的多种指标体系中遴选精度最大的一组建立信用评分模型[17]。ORESKI等将每个客户看作一个染色体,不同的指标看作不同的基因,将0-1标识表示指标是否被选中,通过遗传算法改变0-1标识的值,得到不同的指标组合,并通过神经网络模型遴选一个判别精度最大的指标组合[18]。本文通过0-1整数规划求解最优指标体系组合的思路也是借鉴了文献18中指标标识的优化思路。
在上述四类构建指标体系的方法中,除了文献18外都没有研究考虑指标间的组合方式,由于指标的不同组合方式将构建不同的指标体系。如何在众多的指标体系中遴选出违约鉴别能力最强的一套指标体系是本文的主要研究内容。本文与文献18的主要区别在于文献18通过神经网络判断指标组合的判别精度,而本文提出可以通过似然函数值衡量指标体系的违约鉴别精度。
2 最优信用评价指标体系的构建模型
2.1 基于显著相关性检验的指标遴选
用于评价小企业信用风险的指标纷繁复杂,在这众多的指标中并不是所有的指标有能够识别小企业是否违约,因此本文采用显著相关性检验剔除与违约状态不显著相关的指标。相关系数是对两个指标的密切程度的度量,一般而言相关系数绝对值越大、两个指标之间越相关。现有大量研究通过主观确定临界值来衡量两个指标间的相关系,这种主观确定临界值的方式是不精确地。
显著相关性检验是用来检验指标与违约状态之间是否存在显著线性相关关系的一种方法。根据式(1)可知,样本个数n也会影响到相关系数的大小。因此,显著相关性检验是通过样本数n对相关系数进行修正,构建T统计量来检验指标与违约状态之间的相关性是否显著。T统计量的绝对值越大,指标与违约状态之间的相关性越显著。
式(1)表示第j个指标向量与违约状态向量之间的相关系数,相关系数越大,反映指标与违约状态越相关,即指标越能区分违约和非违约小企业。
第j个指标与违约状态之间的T统计量tj的计算公式如(2)所示:
上述统计量服从自由度为n-2的T分布。通过T分布函数确定统计量tj对应的P值。如果P值小于给定的显著性水平α,检验通过,认为第j个指标与违约状态之间存在显著的相关关系。
2.2 基于0-1整数规划的最优指标体系的确定
2.1中筛选出的指标是与违约状态之间存在显著相关关系的指标。但是最终用来进行信用评价的并不是某一个指标,而是由多个指标构成的指标体系。如何在众多的指标中遴选出一个最优的指标组合构成指标体系?最重要的标准是建立的指标体系具有最强的违约鉴别能力。这涉及到两个科学问题,一是如何衡量指标体系的违约鉴别能力;二是如何遴选违约鉴别能力最强的指标体系。
2.2.1 指标体系违约鉴别能力的确定
通过二元Logit回归模型可以预测每一个小企业的违约概率Pi(yi=1),也就是可以确定在某一临界点下小企业是否违约。对应因变量为0、1虚拟变量的二元Logit回归模型而言,采用极大似然估计法估计其指标的系数βj,其思路是尽可能使得估计的小企业违约状态与实际小企业的违约状态的差异最小、即概率似然最大,也就是估计系数时采用的最大似然函数值,能够保证预测的小企业的违约状态最大程度的接近实际的违约状态,即最大似然函数值能够反映对小企业违约预测的精度,似然函数值越大,对小企业的违约预测越准确,也就是其违约鉴别能力越大。
设:yi-第i个小企业的违约状态,yi=1,表示小企业违约,yi=0,表示小企业不违约;n-小企业的个数,xij-第i个小企业的第j个指标,Pi(yi=1)-第i个小企业违约的概率,zi-中间变量,表达式为不同指标的线性组合,如下文式(4)所示;βj-二元Logit模型中第j个指标对应的系数,是待估计的参数,β0-常数项,m为指标体系中指标的个数。则二元Logit模型为:
其中,zi的表达式为:
zi=β1xi1+β2xi2+…+βmxim+β0
(4)
为使得估计的小企业违约状态与实际小企业的违约状态的差异最小、即概率似然最大,采用概率论中的乘法定理(假设不同小企业贷款之间是独立的),不同小企业同时发生违约或者不违约的概率等于单个小企业发生违约或不违约的概率的乘积。因此得到似然函数表达式:
(5)
对式(5)取对数,对数似然函数值LL:
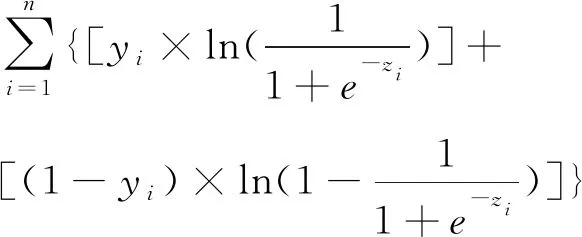
(6)
式(6)含义:式(6)是通过极大似然函数求解二元Logit模型时确定的对数似然函数值LL,通过对数似然函数值最大估计指标系数βj,能够确保估计出的小企业客户的违约状态与小企业实际的违约状态差异最小,即对数似然函数值LL反映(4)中m个指标的整体违约鉴别能力,LL越大,指标体系违约鉴别能力也就越大。
2.2.2 违约鉴别能力最强的指标体系的确定
根据2.2.1的(2)中极大似然函数值能够衡量指标体系违约鉴别能力的标准,更进一步,给定一个指标组合,就可以构造一个二元Logit回归模型,也就是可以确定一个对数似然函数值,在指标体系遴选中,有众多的指标组合,也就是对应众多的对数似然函数,从中确定最大对数似然函数对应的那个指标组合就是最优指标组合。
与违约状态显著相关、可用于信用评价的指标众多,不同指标可以构成不同的指标组合、即指标体系。例如m个指标,有2m-1种组合方式。例如下文实证中m=40,则240-1=1.1×1012,即有1.1万亿种组合方式,如何在这1.1万亿种组合方式中寻找一个违约鉴别能力最强的组合,作为小企业信用评价的指标体系。
对每一个指标都有两种状态,进入指标体系,不进入指标体系两种状态,这符合运筹学中0-1整数规划的特点,故本文采用0-1整数规划进行最优指标体系的确定。
定义:
则上文中的二元Logit模型可以写为:
该模型对应的对数似然函数值LL:
以式(9)的对数似然函数值LL最大为目标函数,建立0-1整数规划,反推出决策变量θ={θ1,θ2,…,θm},以及式(8)对应的最优系数β={β1,β2,…,βm}。此时,θj=1时对应的全部指标构成的指标体系就是违约鉴别能力最大的最优指标体系。
2.2.3 基于遗传算法的0-1整数规划的求解
由式(9)可知本文建立的0-1整数规划属于非线性整数规划,也就是属于具有指数复杂度的NP问题。2.2.2中也提到,如果通过试凑的方式需要尝试1.1万亿次才能找到最优解。
本文选取遗传算法对该问题进行求解,主要原因有三:一是遗传算法的搜索能力强,能得到一个全局效果较优的最优解;二是遗传算法借助于适应度函数即可评估最优解,本文最优指标体系的选择标准也是适应度函数、即对数似然函数值;三遗传算法在搜索最优解时不是采用确定性规则,而是采用概率的思想,从概率意义上找出最优解。
通过遗传算法求解上述非线性整数规划的步骤如下:
Step1初始化:确定迭代的次数、种群的规模以及变异概率。
Step2随机产生初始种群:种群中个体编码长度等于指标个数m。
Step3计算适应度,即计算式(9)中对数似然函数值,该值越大,指标体系越优。
Step4对Step2中的个体进行选择、交叉、变异操作,产生新的种群。
Step5计算新种群的适应度,即计算式(9)中的对数似然函数值。
Step6重复Step4~Step5,确定适应度最大时对应的染色体,即适应度收敛时的决策变量值。此时对应的指标体系,就是违约鉴别能力最大的最优信用评价指标体系。
3 实证研究
3.1 指标及数据的获取
3.1.1 基于5C标准的海选指标体系
以信用5C分析法[2]为标准,以商业银行实际中运用的指标、文献梳理中的指标、以及权威评级机构采用的指标为基础,海选指标,对客户信用风险进行定量分析。最终选择了61个指标,作为小企业信用风险评价的海选指标体系,如表1所示。

表1 基于信用5C评估标准的海选指标体系
3.1.2 数据的获取及处理
参考《巴塞尔新资本协议》第三版中认定的“债务人对于银行集团的实质性信贷债务逾期90天以上”的视为违约,本研究将在“贷款到期日+90天”时的贷款小企业,没有足额偿还的都视为该笔债务违约。选取北京、天津、大连、成都等28个地区的贷款小企业作为对象进行实证研究,数据包括3045笔小企业贷款,其中违约贷款50笔,非违约贷款2995笔。
本文中数据的处理主要包括三类:一是异常值的处理;二是缺失值的补充;三是数据的标准化。
(1)异常值处理方法:计算指标数据的均值μ和标准差σ,通过“μ±2σ”的方法替代异常值,即当指标值大于“μ+2σ”时用“μ+2σ”代替;指标值小于“μ-2σ”时用“μ-2σ”代替。上述处理方式能够保证数据自身的分布特点。
(2)缺失值的补充:本文采取指标的最差值补充缺失值。主要原因是银行更加关注将违约客户识别出来。具体填补方式为,对于值越大越好的正向指标,采用“μ-2σ”替代缺失值,对于值越小越好的负向指标,采用“μ+2σ”替代缺失值。
(3)数据的标准化:为了消除量纲的影响,将数据进行标准化处理,转化为[0,1]区间内的标准化数值。数据标准化参考文献10,本文不再赘述。
对经过上述处理的3045个小企业的61个指标进行描述性统计分析,如表2所示。
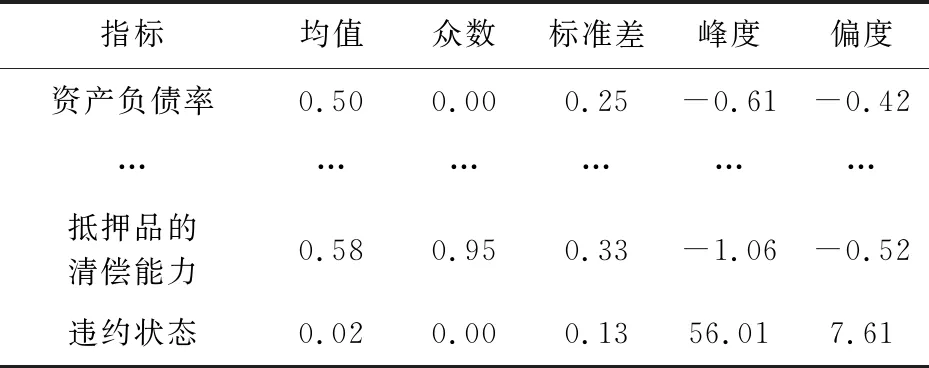
表2 61个海选指标的描述性统计分析结果
3.2 基于显著相关检验的有效指标筛选
将61个指标数据x与违约状态y带入相关系数计算公式(1),得到每一个指标与违约状态之间的相关系数,列入表3第2列。将表3第2列的相关系数r、小企业数目n=3045带入式(2),得到每一个指标与违约状态之间的T统计量的值,列入表3第3列。
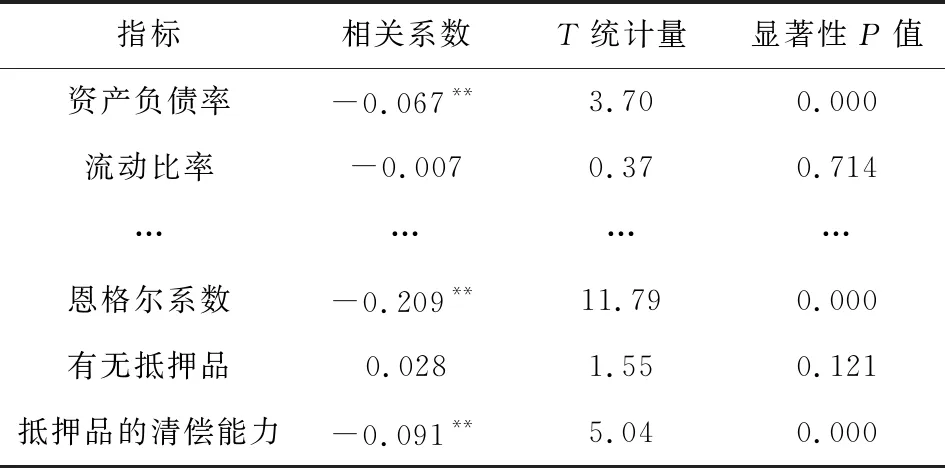
表3 61个指标相关系数及检验结果
通过查询自由度为n-2=3043的T分布表,得出在表3第3列统计量tj对应的P值,列入表3第4列。给定显著性水平α=0.05,如果表3第3列的P值小于0.05,则检验通过,认为该指标与违约状态之间存在显著的相关关系,该指标可以用来进行信用风险评价。
通过上述过程,在61个海选指标中,删除流动比率等21个指标,保留资产负债率、恩格尔系数、等40个与违约状态具著相关性的指标。
3.3 基于0-1整数规划的小企业信用风险最优评价体系
采用Matlab中的遗传算法工具箱进行优化求解。其中参数设置为最大代数为500,最大停滞代数是100,种群规模为是1000,求解以式(9)的对数似然函数值LL为目标函数,以指标系数θj=1代表入选体系,θj=0代表未入选指标体系,以θj为决策变量,建立0-1整数规划,反推一组θj值使得对数似然函数值最大。此时,θj=1对应的指标构成的指标体系就是最优指标体系。
通过上述求解,在3.2中确定的40个指标中,最终决策变量θ={θ1,θ2,…,θm}中θj=1的指标有17个,此时目标函数最大值、即最大似然函数值为13641.5。即小企业信用风险最优评价指标体系包括17个指标,具体如表4第2列所示。

表4 小企业信用风险最优评价体系
3.4 对比分析
对比模型如下:
模型1本文似然函数视角下小企业信用风险最优评价体系,将表4中的17个指标列入表5第2列。

表5 指标体系的对比分析
模型2选出最优的前m=17个指标构成体系。即指标与违约状态的显著相关性,选出与违约状态最相关、即t统计量值最大的前17个指标,列入表5第3列。
模型3向前搜索方法构建的指标体系。即先确定40个指标中每一个指标的极大似然函数值,遴选出最大的一个,并将其分别于其他39个指标组合,计算39个指标的极大似然函数值,遴选出最大的一组中的2个指标;再将这2个指标分别与剩余的38个组合,重复上述过程,直至指标体系的极大似然函数值不再继续增大为止。筛选出的指标如表5第4列模型3所示,共有8个指标。
模型4向后搜索方法构建的指标体系。即先确定全部40个指标的极大似然函数值,任意删除一个指标,计算40个含有39个指标体系的极大似然函数值,保留极大似然函数值最大的那一组,并任意删除一个指标,计算39个含有38个指标体系的极大似然函数值,重复此过程,直至指标体系的极大似然函数值不再继续增加为止。筛选出的指标如表5第5列模型4所示,共有35个指标。
虽然根据式(9)中的似然函数能够衡量指标体系的好坏,但是避免按照本文标准引起误解,以传统的违约判别精度为标准。即分别以上述四种模型构建的指标体系为基础,将其带入二元Logit回归模型中,预测小企业的违约概率,并以0.5为临界点对其是否违约进行判定,4种模型的混淆矩阵及判别精度如表6所示。

表6 4种模型对应的混淆矩阵结果
通过表6的结果可知,本文提出的模型1对违约状态的判别具有更高的精度为98.8%,模型2的精度为98.4%,模型3的精度为98.4%;前3个模型的精度都高于模型4的精度97.5%。前3个模型的精度虽然看起来相差不大,但是在对违约客户和非违约客户的分类上差别很大,具体为:
模型2和模型3中将违约客户判错为非违约客户的错判率高达50/50=100%,模型1将违约客户错判为非违约客户的错判率为34/50=68%,远远小于模型1的错判率。而银行更看重模型对违约客户的识别精度,因为一旦违约客户被识别为非违约,给银行带来的是直接损失;而将非违约判别为违约,损失的仅是一个客户。二者对银行的影响存在质的差别。因此,本文提出的指标体系比现有前项搜索算法、后项搜索算法、单一指标遴选方法构建的指标体系具有更高的整体违约判别精度。
4 结论与展望
合理评价小企业的信用风险,有利于改善小企业融资难的现状,促进金融发展和增加就业。建立小企业信用评价指标体系是评价贷款小企业信用风险的前提和基础。本文以中国某商业银行分布在28个城市的小企业贷款数据为实证样本,通过以下两个步骤构建小企业信用风险最优评价体系,一是通过显著相关性检验,删除与小企业违约与否没有显著相关的指标,解决了在众多指标中,遴选出具有违约判别能力的指标。二是在具有违约判别能力的指标具有不同的组合方式,不同的组合方式构成不同的指标体系,本文提出了通过对数似然函数值衡量指标及指标体系违约判别能力这一新的标准,以对数似然函数值最大为目标函数,构建0-1整数规划,通过遗传算法求解出违约鉴别能力最大的小企业信用风险评价指标体系。
通过上述两个步骤,最终建立了一套涵盖了“营业利润率”、“小企业授信情况”、“恩格尔系数”、“抵押品的清偿能力”等17个指标的信用风险最优评价体系。并将本文构建的指标体系,与前向搜索算法、后向搜索算法、以及单一指标筛选方法构建的指标体系进行对比,通过混淆矩阵确定的整体判别精度和第二类错误,确定本模型构建的指标体系具有更高的违约风险判别精度。
研究展望:本文通过删除与小企业违约与否没有显著相关的无效指标,在剩余指标的不同组合中遴选一个违约鉴别能力最大的指标组合构成小企业信用风险最优评价体系。在这个过程中,没有考虑单一指标无效,但是多个无效指标组合在一起未必无效,因此,下一步的研究将考虑不删除单一无效指标,而是在全部指标的不同组合中遴选最优指标体系。

