具有联盟结构的Banzhaf值
单而芳, 吕文蓉, 史纪磊,2
(1.上海大学 管理学院,上海 200444; 2.宁波财经学院 基础学院,浙江 宁波 315175)
0 引言
效用可转移合作对策[1](简称TU-对策)是描述参与者通过联盟进行合作并产生收益的一种基本模型。该模型假设任何有限参与者的集合均能形成可行联盟进行合作。在这个基本假设下,SHAPLEY[2]提出了如何公平合理地分配合作利益的分配规则,也就是著名的Shapley值。Shapley值的主要思想是利用公理化方法,根据参与者对联盟的边际贡献来决定利益的分配。此外,BANZHAF[3]依据投票对策的背景,提出了合作对策中另一个重要的分配规则—Banzhaf值。之后,OWEN将Banzhaf值推广到一般合作对策中[4]。与Shapley值相比,Banzhaf值也是考虑每个参与者对所有联盟边际贡献的期望值来决定对这个参与者的支付。不过,这两个值所考虑的参与者加入每个联盟的可能性(概率)是不同的,Banzhaf值假定参与者加入任何规模的联盟的可能性是一样的,而Shapley值仅假定参与者加入任何相同规模的联盟的可能性是相同的。
然而,在实际中,参与者之间为了达到某种目的可能会结成所谓的优先联盟。1974年,AUMANN和DRÉZE首先研究了具有联盟结构的TU-对策模型[5],每个联盟结构定义为大联盟的一个划分,划分中的每个子集称为一个优先联盟。而后,OWEN[6]假设任何优先联盟既可以与其他优先联盟也可以与其他优先联盟中的部分参与者形成更大的联盟进行合作。以此为前提并借助Shapley值,提出了相应的分配规则—Owen值。 Owen值是首先将每个优先联盟作为参与者进行Shapley值分配,然后再在每个优先联盟内利用Shapley值进行二次分配。Owen值最吸引人的性质之一是它的商对称性,该性质要求在商对策中扮演对称角色的两个联盟其获得的收益是相同的。在这一假设下,OWEN[7]进一步讨论了具有联盟结构的TU-对策的Banzhaf值,并提出了Banzhaf-Owen值。2009年,KAMIJO[8]考虑了不同于Owen假设的情况,他假设每个优先联盟的参与者只能作为整体与其他优先联盟形成更大的联盟进行合作。在此假设下,借助Shapley值,提出了该假设下TU-对策的一种新的分配规则,称为Ka值。为加以区别,他将基于Owen假设下的分配规则统称为联盟值,而该假设下的分配规则统称为集体值[9]。关于Banzhaf值和具有优先联盟结构的其他研究可以参看文献10~14。
在实际中,经常需要考虑KAMIJO假设下的集体值。例如,某公司举行股东大会进行决策,由于各个股东的持股数不同,对应的投票权力也不一样。一些理念一致或者相近的股东为了达到某种目的会组成所谓的优先联盟。由此形成的优先联盟都作为整体来参与决策,以更多股数的优势提高在决策或谈判中的议价能力来获取更多的收益,然后再在优先联盟内部分配既得利益。此时可以考虑利用集体值来估计各个股东的权力指数。为了更好估计这类问题中不同参与者的权力指数,作为起源于投票对策的Banzhaf值,定义KAMIJO假设下的Banzhaf值是十分必要的。本文的目的是在KAMIJO假设下提出具有联盟结构TU-对策的Banzhaf值,并给出它的公理化刻画。
本文的下一节将给出TU-对策的一些基本定义和记号。第三节提出具有联盟结构的Banzhaf值的表示式,并进行公理化刻画。第四节以某公司股东大会决策为例,讨论了具有联盟结构的Banzhaf值的应用,并与Banzhaf-Owen值、对称联盟Banzhaf值等做了比较分析。最后,总结了本文所做的工作。
1 预备知识
1.1 TU-对策
效用可转移合作对策可由二元组(N,v)表示,其中N={1,2,…,n}表示参与者的集合,v是定义在2N→R上的一个映射,称为特征函数,且规定v(Ø)=0。N被称为大联盟,N的每个非空子集S被称为一个联盟,而v(S)表示联盟S中成员进行合作所获得的效用。记所有N上的TU-对策集合为VN。为方便起见,通常将v({i,j,…,k})简记为v(i,j,…,k),相应的也将S∪{i}和N{i}分别简记为S∪i和Ni。
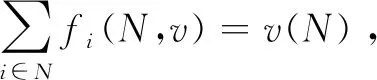
另一个被广泛应用的单值解是Banzhaf值Ba(N,v),它起源于投票对策,其定义为:
1.2 具有联盟结构的TU-对策
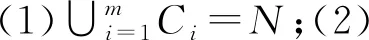
三元组(N,v,C)表示具有联盟结构的TU-对策,其中(N,v)表示TU-对策,(N,C)表示联盟结构。记所有具有联盟结构的TU-对策集合为U(N)。对于任意(N,v,C)∈U(N),且C={Cr|r∈M={1,2,…,m}},其商博弈定义为(M,vC),其中M是参与者集,且对任意的R⊆M,有vC(R)=v(∪r∈RCr)。
若对任意(N,v,C)∈U(N)都有唯一的支付向量f(N,v,C),则称f为具有联盟结构的TU-对策的一个解或者值。
对任意(N,v,C)∈U(N),Owen值Φ定义为:
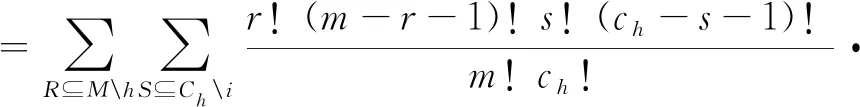
[v(Q∪S∪i)-v(Q∪S)]
(2)
其中i∈Ch∈C,Q=∪r∈RCr。
Banzhaf-Owen值Ψ以及对称联盟Banzhaf值分别定义为:
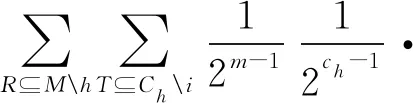
(v(Q∪T∪i)-v(Q∪T))
(3)
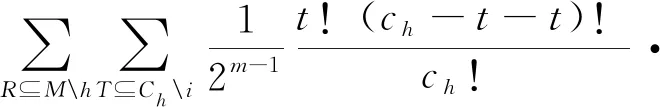
(v(Q∪T∪i)-v(Q∪T))
(4)
其中Q=∪r∈RCr。
KAMIJO[8]假设只有完整优先联盟之间才能进行充分合作而产生联盟效用。具体地,对于任意的S⊂Ck∈C和Cs∈C,且k≠s,优先联盟Ck与Cs中所有成员参与合作时,可获得收益v(Ck∪Cs);而当S与Cs合作时,仅能获得收益和v(S)+v(Cs)。在这个基础之上,对任意的分割C={Cr|r∈M={1,2,…,m}},以及任意的联盟S⊆N且S≠Ø,KAMIJO定义S/C={∪{r∈M|S∩Cr=Cr}Cr}∪{S∪Cr|S∪Cr≠Cr,r∈M}。对任意的(N,v,C)∈U(N),由联盟结构C导出的分割限制对策(N,v|C)的特征函数定义为:对任意的S⊆N,
(5)
对任意的(N,v,C)∈U(N),Ka值定义为:Ka(N,v,C)=Sh(N,v|C)。
2 具有联盟结构的Banzhaf值及其公理化刻画
2.1 具有联盟结构的Banzhaf值
根据上述理论, 结合式(1)和式(5),本文定义一种新的具有联盟结构的Banzhaf值,简称为C-Banzhaf值。
定义1(C-Banzhaf值) 对于任意的(N,v,C)∈U(N),C-Banzhaf值ξ可定义如下:对任意的i∈N,
ξi(N,v,C):=Bai(N,v|C)
(6)
2.2 C-Banzhaf值的公理化刻画
分割内合并性(Pairwise Merging of Partition)。对任意的(N,v,C)∈U(N),i,j∈Ck∈C,f∈Rn,若分配规则满足
fi(N,v,C)+fj(N,v,C)=fp(Nij,vij,Cij)
则称f具有分割内合并性,其中具有联盟结构的对策(Nij,vij,Cij)定义为:参与者集合Nij是指用p代替参与者i,j,即:Nij=(N{i,j})∪{p};联盟结构Cij定义为:若i,j∈Ck,令Ck′=(Ck{i,j})∪{p},则Cij=(CCk)∪Ck′。
对任意的T⊆Nij,
这个性质是指:同属一个优先联盟内的任意两个参与者合并后的收益,与这两个参与者的收益之和相等。与Banzhaf值的2-有效性不同之处在于2-有效性一次合并仅能发生在一对参与者之间,而联盟结构使得不同优先联盟内的合并互不干扰,即:当任意k∈M,都有|Ck|≥2时,一次合并最多可发生在m对参与者之间。
例1考虑具有联盟结构的对策(N,v,C)∈U(N),其中参与者集合为n={1,2,…,6},联盟结构为C={{1},{2,4},{3,5,6}},收益为1时的最小联盟为:{1,2},{1,3},{1,4},{1,5},{1,6},{2,3,4,5,6}。
根据式和式可计算得:ξ1(N,v,C)=10/25,ξ2(N,v,C)=ξ4(N,v,C)=8/25,ξ3(N,v,C)=ξ5(N,v,C)=ξ6(N,v,C)=4/25。现同时合并2,4为p1,合并3,5为p2,可得新联盟结构C′为:C′={{1},{p1},{p2,6}},同理可计算得:ξp1(N,v,C)=1/2=ξ2(N,v,C)+ξ4(N,v,C),ξp2(N,v,C)=1/4=ξ3(N,v,C)+ξ5(N,v,C)。显然,不同优先联盟内合并互不干扰。且对于该对策,一个合并最多可发生在两对参与者之间。
为了给出C-Banzhaf值ξ的公理化刻画,我们引入下列新的性质。
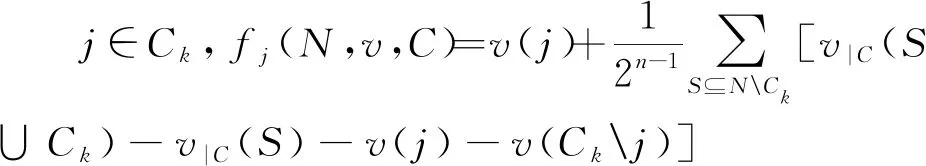
这个性质是指:对由单独参与者或者两个参与者形成的优先联盟,给其中参与者的支付等于这个参与者独自的效用加上分割限制对策下该参与者所在优先联盟对其他所有普通联盟的边际贡献再减去优先联盟中参与者的效用和的期望值。特别地,当大联盟N={i}时,则有fi(N,v,C)=v(i)。而当大联盟N={i1,i2}并且优先联盟为C={N}时,则有fi1(N,v,C)=v(i1)+1/2[v(i1,i2)-v(i1)-v(i2)]和fi2(N,v,C)=v(i2)+1/2[v(i1,i2)-v(i1)-v(i2)]。
接下来给出本文的主要结论。
引理1对任意的(N,v,C)∈U(N),C-Banzhaf值ξ(N,v,C)满足标准性。
定理1对任意的(N,v,C)∈U(N),C-Banzhaf值ξ(N,v,C)可由分割内合并性和标准性所唯一确定。
3 应用算例
股东大会是股份公司的最高权力机关,它由全体股东组成,对公司重大事项进行决策,有权选任和解除董事,并对公司的经营管理有广泛的决定权。本节以某公司举行股东大会进行决策为背景,利用C-Banzhaf值给出各个股东的权力指数,并与其他指数进行对比分析。
例2假设某公司的股东及各股东的持股数情况如下:A股东28股,B股东16 股,C股东5股,D股东4股,E股东3股以及F股东3股。当支持某候选董事的股数大于等于30时该董事的任选,且各股东间存在的优先联盟情况为:C={{A},{B,D,F},{C,E}}。现将该公司举行股东大会推选董事的过程抽象为一具有联盟结构的TU-对策作如下分析。
我们可以把上述问题归结为如下的合作对策(N,v)模型:N表示所有股东的集合,而特征函数v的取值为0或者1。在对策论中,把此类对策被称为简单对策。在简单对策中,若v(S)=1,则称联盟S为获胜联盟;否则为S失败联盟。若一个获胜联盟的所有真子集都是失败的,则称该获胜联盟为极小获胜联盟。简单对策常用于投票选举中。在简单对策中各类值均可视为一种权力指数,用来度量联盟内各成员的权力。
由假设可知,在该公司推选董事的过程中,极小获胜联盟为:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C,D,E,F}。根据式(1)和式(6),计算可得C-Banzhaf值ξ如表1所示,表中同样列出了由式(2)、式(3)和式(4)分别计算得到的Owen值(φ)、Banzhaf-Owen值ψ以及对称联盟Banzhaf值Π。
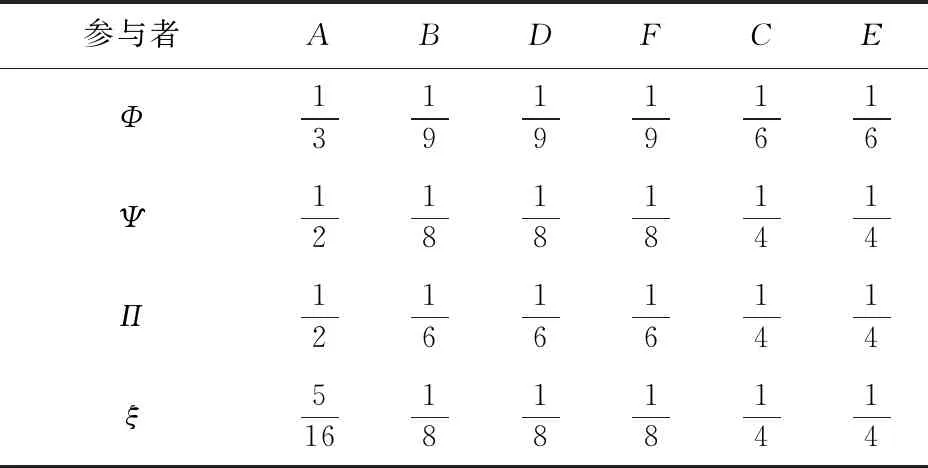
表1 各值计算结果
从表格数据可已发现,Owen值与对称联盟Banzhaf值在三个优先联盟间的分配之和是相等的,这表明三个优先联盟在决定哪个候选董事任选的过程中,发挥的作用是相同的事实上,三个优先联盟发挥的作用是不对称的。就A股东所在的优先联盟而言,该优先联盟只含A股东,但拥有的股数却比其他任何一个优先联盟中所有股东的股数之和还要多。所以,该优先联盟在决定候选董事的过程中发挥的作用远大于其他优先联盟。因而,使用Banzhaf-Owen值或C-Banzhaf值分配更具有现实意义。而对于这两个值的选择,则需考虑决策联盟中是否存在不可分割的利益共同体以及优先联盟的风险意识。若优先联盟更倾向于保守选择,确保自己有利可得,则优先考虑使用Banzhaf-Owen值;相反,若优先联盟更倾向于以自身强大的议价能力谋求更多的利益,则可优先考虑使用C-Banzhaf值。
4 结论
首先,本文定义了一种新的具有联盟结构的Banzhaf值(C-Banzhaf值),并通过分割内合并性和标准性给出了C-Banzhaf值的唯一性刻画,完善了Banzhaf值的相关理论。其次,本文考虑拥有投票权的群体中,可能存在不同性质的优先联盟结构,讨论了C-Banzhaf值的应用,并对比分析了C-Banzhaf值的适用范围。事实上,股东之间的合作行为不仅受其优先联盟结构的影响,有时还会受股东之间通讯的影响,这会产生网络(图)结构。因此可以进一步研究C-Banzhaf值在图结构下的形式和相关的公理性刻画。
致谢: 衷心感谢评审人和分区主编提出的宝贵建议。

