闭环供应链中再制品价格欺骗的均衡路径分析
杨明歌, 盛 鑫, 梁小珍
(上海大学 管理学院,上海 200444)
0 引言
制造业的快速发展使得工业产品报废率处于较高水平,废旧品的再制造问题受到极大关注。1999年,“再制造”由中国工程院院士徐滨士[1]在西安召开的“先进制造技术国际会议”上率先提出。再制造不仅可以解决环境恶化和资源短缺的问题,还可以为企业带来经济效益。近年来,再制造环节中的产品回收和产品生命周期支持过程中的逆向物流受到越来越多的重视,传统供应链纷纷向闭环供应链转变。闭环供应链是企业从采购到最终销售以及废旧品再制造、再销售的完整供应链循环。
闭环供应链中再制造相关问题已经被学者们广泛研究,目前主要集中在三个方面:第一,再制造进入决策问题。例如,郭军华等[2]在消费者支付意愿存在差异的条件下,分别研究有无竞争环境下的OEM再制造商进入决策的边界条件。石岿然等[3]运用演化博弈研究UOEM参与再制造的进入博弈,以及OEM的应对策略。第二,再制造的回收策略选择。2004年,SAVASKAN等[4]比较制造商、零售商及第三方企业负责回收的三种模式对再制造各利益相关方的策略选择的影响。2006年,SAVASKAN和VAN EISENHOWER[5]在零售商竞争环境下分析再制造的回收渠道选择问题。随后,许多学者沿着文献5的研究思路,将废旧品回收问题拓展到更复杂的情况。周永圣和汪寿阳[6]在政府监控情形下分析制造商、零售商和第三方物流回收模式对回收价格和企业利润的影响。王文宾和达庆利[7]在考虑消费者偏好变化下分别研究零售商和第三方企业回收对回收努力程度和企业利润的影响。第三,政府干预下的再制造协调机制。例如,MITRA和WEBSTER[8]建立两阶段的再制造系统中制造商和再制造商的竞争模型,分析政府补贴对系统的影响。ATASU等[9]建立政府、生产商和消费者之间的博弈模型,分析政府补贴对生产商回收再制造废弃电子产品的影响。WRIGHT等[10]讨论政府如何干预需求才能促进逆向物流环境下的废弃物回收循环。
文献2~10从进入决策、回收策略和协调机制等前向环节研究再制造,尚未有文献从再制品销售这一后向环节研究再制造。实际上,再制造的后向销售环节也存在很多问题。例如,再制品销售商为了获得更多的利润,通常会花费一定的伪装成本,将再制品伪装成新产品,并以新产品的价格出售伪装后的再制品。这种行为即再制品价格欺骗,不仅损害消费者的利益,而且阻碍再制品市场的良性发展,故本文研究闭环供应链后向销售环节的再制品价格欺骗问题,探讨其内在机制和解决方案。
已有文献主要从伪装成本的角度研究欺骗问题。陈杰等[11]在生态供应链下分析供应商将产品粉饰成绿色产品的伪装成本对供应商和制造商策略选择和利润的影响。张国兴等[12]在考虑政府节能减排政策下分析伪装成本和期望风险成本对企业和政府策略的影响。岳柳青和刘咏梅[13]针对“公司+农户”组织模式中农户发生机会主义行为的现象,研究农户隐瞒生产信息所产生的伪装成本对不同市场均衡的影响。文献11~13中的伪装成本均为伪装主体粉饰原始商品的成本,即狭义的伪装成本。此时,伪装成本主要与伪装主体的伪装能力有关,通常是常数,难以调控。若将伪装成本理解为伪装主体为其伪装行为付出的全部代价,不仅包括交易之前的粉饰成本,还包括事后被追责的代价,即广义的伪装成本,则伪装成本就是变量,可以调控。考虑到再制品市场的价格欺骗事件层出不穷,亟需政府干预,故本文在研究再制品价格欺骗时,先考虑狭义的伪装成本,再考虑广义的伪装成本,并对两种结果进行比较。政府的奖励或惩罚措施可以影响销售商事后被追责的代价,进而调控伪装成本。
文献11~13运用信号博弈研究欺骗问题,信号博弈要求博弈方是完全理性的,且博弈是不完全信息的。然而,在真实的市场环境中,参与者做到完全理性只是理想状态。演化博弈不要求博弈方是完全理性的,也不要求博弈是完全信息的,更符合实际情况,故本文运用演化博弈研究闭环供应链中的再制品价格欺骗问题。首先,建立销售商和消费者的双方演化博弈模型,研究销售商和消费者的行为演化规律;其次,考虑政府的奖励和惩罚措施对再制品市场的影响,建立销售商、消费者和政府的三方演化博弈模型,研究销售商、消费者和政府的行为演化规律;最后,通过数值分析验证相关模型结论的正确性,为政府提供相关建议。
1 符号说明和模型假设
本文研究一个由销售商和消费者构成的再制品市场。在这个市场中,销售商的产品来源全为再制品,且销售商具有将再制品伪装成新产品进行售卖的能力;消费者并不知道市场中产品的来源情况,但销售商清楚地知道产品的来源情况。基于利益驱动,销售商会进行再制品价格欺骗。
1.1 符号说明
Pn:新产品零售价;
Pr:再制品零售价;
Vn:消费者对新产品的支付意愿;
Vr:消费者对再制品的支付意愿;
Wr:单位再制品的生产成本(或批发成本);
C0:销售商将单位再制品粉饰成新产品的成本;
C1:政府检查单位产品的成本;
S:政府检查且销售商不伪装时政府对销售商的单位产品给予的奖金;
T:政府检查且销售商伪装时政府对销售商的单位产品收取的罚金。
1.2 模型假设
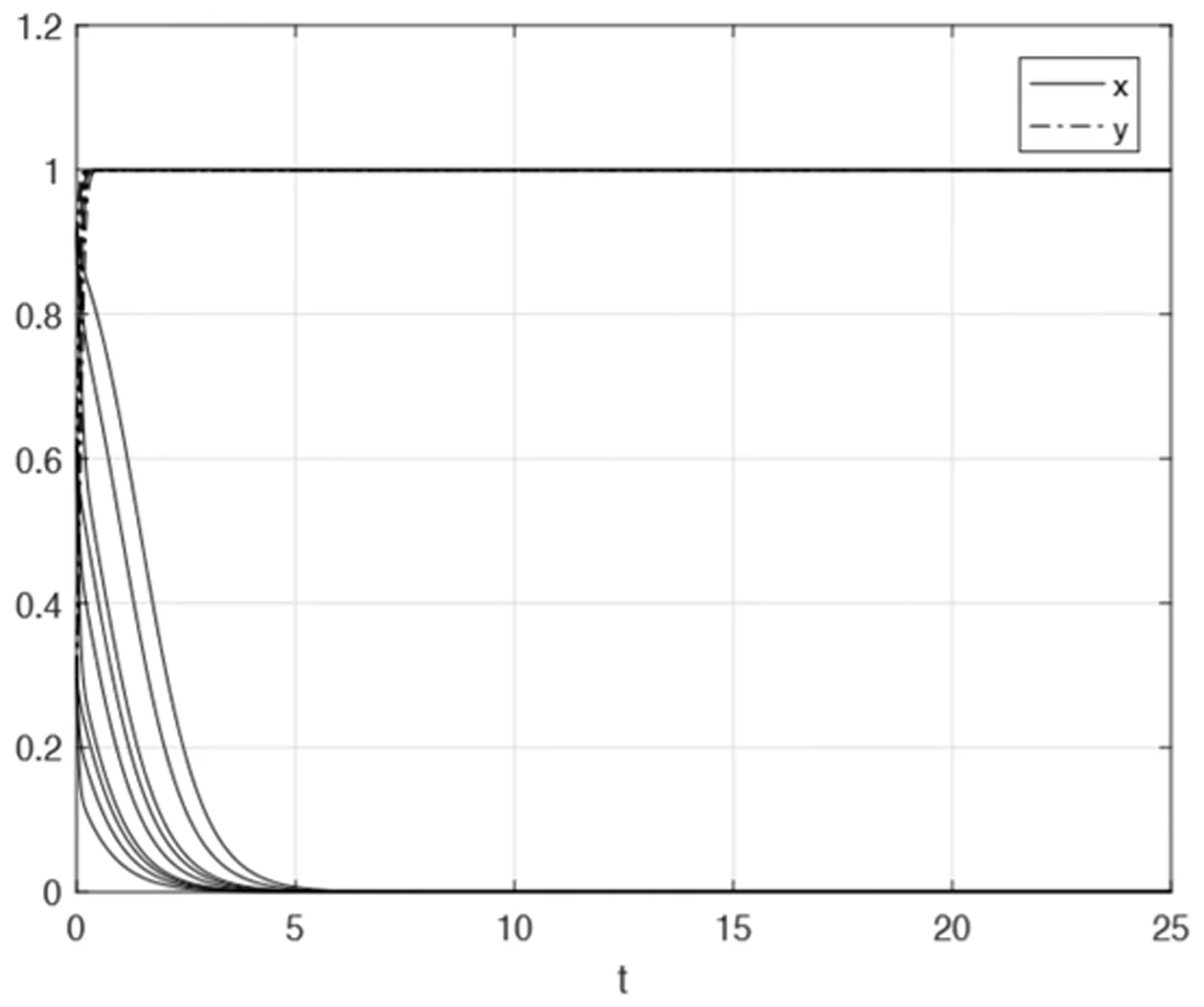
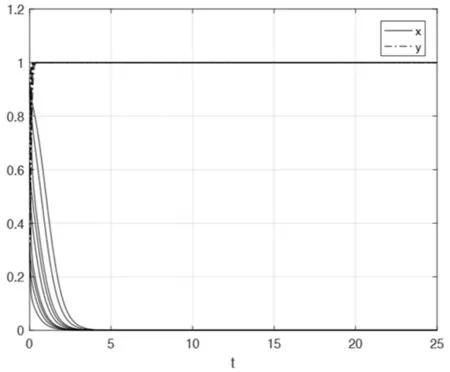
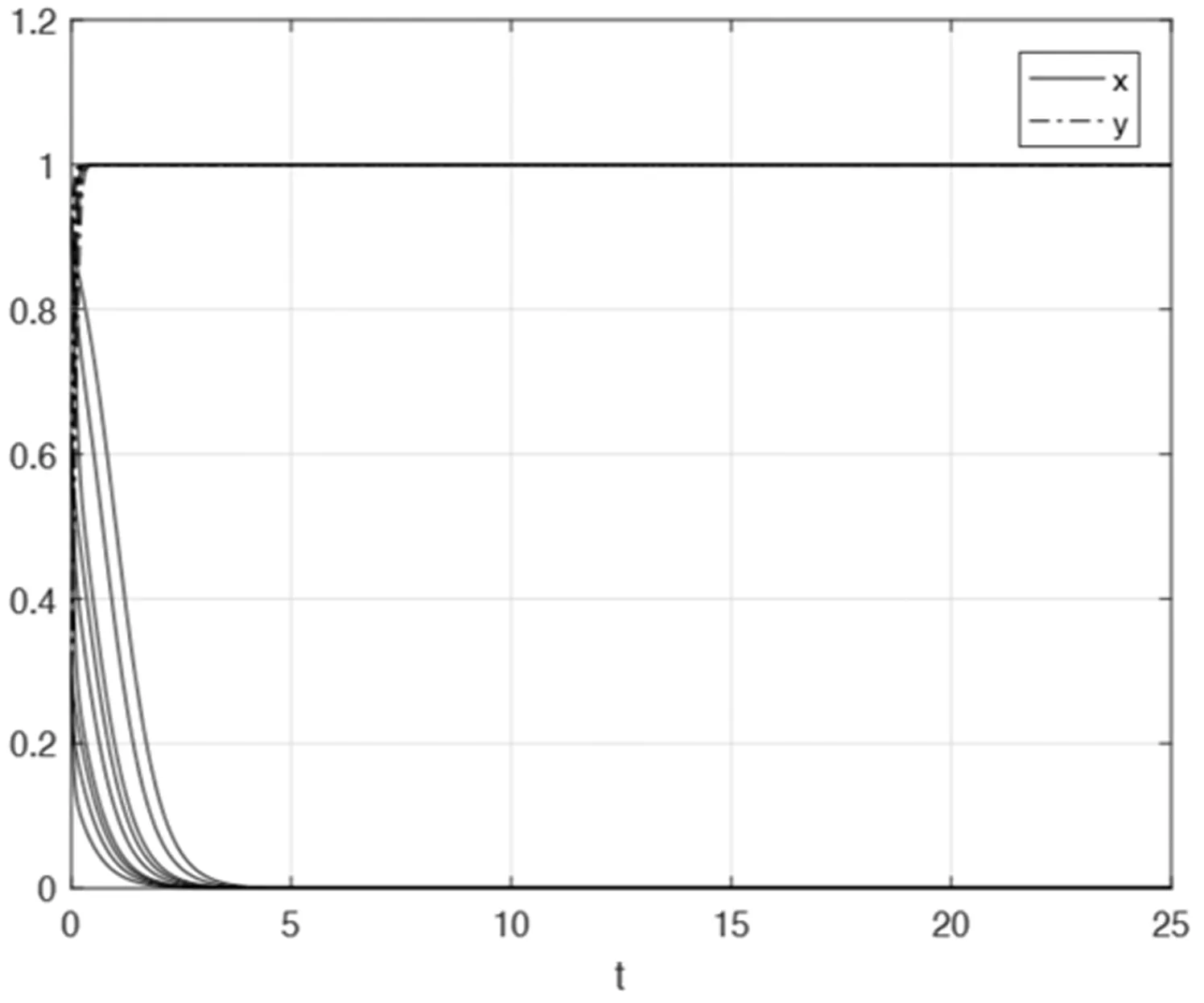
假设1再制品与新产品不同质,且消费者对再制品的接受程度较低,故再制品的价格低于新产品的价格,即0 假设2再制品的生产成本低于新产品的生产成本,再制品的批发成本低于新产品的批发成本。 假设3消费者对新产品的支付意愿大于新产品的零售价,即Vn>Pn。同理,消费者对再制品的支付意愿大于再制品的零售价,即Vr>Pr。 假设4当政府检查再制品市场时,完全可以分辨出销售商是否存在伪装售卖再制品的行为。 假设5销售商、消费者和政府均为风险中性。 本节构建一个由销售商和消费者组成的双方博弈G1。记N={1,2}表示参与该博弈的博弈方集合,其中,1代表销售商,2代表消费者。销售商的策略集S1={伪装,不伪装},消费者的策略集S2={购买,不购买},博弈G1的策略空间S为所有博弈方策略集的笛卡尔乘积,即S=S1×S2={(伪装,购买),(伪装,不购买),(不伪装,购买),(不伪装,不购买)}。任意的i∈N,设博弈方的效用函数为Ui,则该博弈可以记为G1=[N,S,{Ui}i∈N]。 博弈中的效用函数可以用收益函数来代替,这里消费者的收益指的是消费者剩余,故销售商和消费者双方博弈的收益矩阵为 假设在销售商和消费者的演化博弈过程中,销售商选择“伪装”的概率为x,选择“不伪装”的概率为1-x;消费者选择“购买”的概率为y,选择“不购买”的概率为1-y。结合表1中的收益矩阵,得到销售商“伪装”的期望收益为 表1 双方博弈的收益矩阵 E1Y=y(Pn-Wr-C0)+(1-y)(-C0) =y(Pn-Wr)-C0 (1) 销售商“不伪装”的期望收益为 E1N=y(Pr-Wr)+(1-y)·0=y(Pr-Wr) 故销售商的期望收益为 =xy(Pn-Pr)-xC0+y(Pr-Wr) (2) 根据Malthus方程[14],得到销售商的复制动态方程为 将(1)和(2)代入(3)得 (4) 同理,可得消费者的复制动态方程为 (5) Jacobi矩阵局部分析法最早出现在文献15中,它是一种利用状态方程解的特性来判断系统稳定性的方法。FRIEDMAN[16]采用该方法求解博弈微分方程的演化稳定策略。下面使用Jacobi矩阵局部分析法求解系统的演化稳定策略。 由方程组(6)求出系统的Jacobi矩阵为 表2 矩阵J在各均衡点处的行列式和迹 命题1(1)当Pn-C0>Pr且Vr>Pn时,(1,1)为系统的演化稳定策略;(2)当Pn-C0 命题1给出销售商和消费者在不同条件下的演化稳定策略,下面进一步分析演化结果并作出经济管理意义上的解释。 当Pn-C0>Pr且Vr>Pn时,(1,1)为演化稳定策略。在再制品市场中,对于销售商而言,是否选择伪装售卖再制品,要受再制品的伪装成本、再制品零售价、新产品零售价和消费者是否购买等因素的影响;对于消费者而言,是否选择购买,要受消费者对再制品的支付意愿、再制品零售价和新产品零售价等因素的影响。在再制造技术不断发展的今天,再制品的质量得到了很大提高,销售商将再制品粉饰成新产品的伪装成本就会降低。由于再制品质量的不断提高,且再制品具有节能环保的特点,故消费者越来越关注和支持再制品,导致消费者对再制品的支付意愿越来越高。当再制品伪装之后的销售价格与伪装成本的差大于再制品不伪装时的销售价格(Pn-C0>Pr)时,销售商选择伪装并成功出售的收益大于选择不伪装并成功出售的收益。当消费者对再制品的支付意愿大于再制品伪装之后的销售价格(Vr>Pn)时,消费者无论选择购买没有伪装的再制品还是选择购买伪装之后的再制品均有利可图。此时,双方的演化稳定策略为(1,1),即销售商选择伪装策略,消费者选择购买策略,同时,再制品市场达到有效状态。 当Pn-C0 当Pn-C0>Pr且Vr 当Pn-C0 综上可知,当Pn-C0 考虑到再制品市场发展初期价格欺骗频频出现,亟需政府管控,故将政府作为博弈第三方考虑进来。在销售商和消费者的双方演化博弈中,再制品的伪装成本仅取决于销售商。一旦政府进行干预,伪装成本就不仅包括销售商将再制品粉饰成新产品的成本C0,还包括政府对销售商诚实出售再制品的奖励,以及对销售商伪装售卖再制品的惩罚,故三方演化博弈中再制品的伪装成本由销售商和政府共同决定。 本节构建一个由销售商、消费者和政府组成的三方博弈G2。记N={1,2,3}表示参与该博弈的博弈方集合,其中,1代表销售商,2代表消费者,3代表政府。销售商的策略集S1={伪装,不伪装},消费者的策略集S2={购买,不购买},政府的策略集S3={检查,不检查},博弈G2的策略空间S为所有博弈方策略集的笛卡尔乘积,即S=S1×S2×S3={(伪装,购买,检查),(伪装,购买,不检查),(伪装,不购买,检查),(伪装,不购买,不检查),(不伪装,购买,检查),(不伪装,购买,不检查),(不伪装,不购买,检查),(不伪装,不购买,不检查)}。任意的i∈N,设博弈方的效用函数为Ui,则该博弈可以记为G2=[N,S,{Ui}i∈N]。 博弈G2中的效用函数可以用收益函数来代替,这里消费者的收益指的是消费者剩余。当销售商选择伪装策略且消费者选择购买策略时,销售商侵犯了消费者的商品知情权,原本消费者支付Pn的价格是为了购买新产品,实际上却购买了再制品,此时消费者的损失为(Vn-Pn)-(Vr-Pn),即Vn-Vr。在计算政府的收益函数时,考虑消费者的这一部分损失。当政府检查时,三方博弈G2的收益矩阵见表3;当政府不检查时,三方博弈G2的收益矩阵见表4。 表3 政府检查时三方博弈的收益矩阵 表4 政府不检查时三方博弈的收益矩阵 假设在销售商、消费者和政府的三方演化博弈过程中,销售商选择“伪装”的概率为x,选择“不伪装”的概率为1-x;消费者选择“购买”的概率为y,选择“不购买”的概率为1-y;政府选择“检查”的概率为z,选择“不检查”的概率为1-z。结合表3和表4中的收益矩阵,得到销售商“伪装”的期望收益为 E1Y=(1-y)z(-C0-T)+(1-y)(1-z) (-C0)+yz(Pn-Wr-C0-T)+ y(1-z)(Pn-Wr-C0) =y(Pn-Wr)-zT-C0 (7) 销售商“不伪装”的期望收益为 E1N=(1-y)zS+y(1-z)(Pr-Wr)+ yz(Pr-Wr+S) =y(Pr-Wr)+zS 故销售商的期望收益为 =xy(Pn-Pr)-xz(T+S)+y(Pr-Wr)-xC0+zS (8) 根据Malthus方程,得到销售商的复制动态方程为 将(7)和(8)代入(9)得 同理,可得消费者的复制动态方程为 政府的复制动态方程为 文献17、18采用分步分析法求解三方演化博弈,该方法实际上是将三方博弈转化为两个双方博弈,运用Jacobi矩阵局部分析法进行求解。本节使用分步分析法求解三方演化博弈,详细探究两两博弈方的演化结果。首先,将变量z看作常量,分析销售商和消费者之间的演化稳定策略;其次,将变量y看作常量,分析销售商和政府之间的演化稳定策略;最后,综合分析整个三方博弈系统的演化稳定策略。 由方程组(13)求出销售商和消费者双方演化系统的Jacobi矩阵为 表5 矩阵J在各均衡点处的行列式和迹 由命题2可得销售商和消费者双方均衡策略的稳定性分析结果,见表6。 表6 销售商和消费者均衡策略稳定性分析结果 由方程组(13)求出销售商和政府双方演化系统的Jacobi矩阵为 表7 矩阵在各均衡点处的行列式和迹 由命题3可得销售商和政府双方均衡策略的稳定性分析结果,见表8。 表8 销售商和政府均衡策略稳定性分析结果 命题2和命题3给出了销售商、消费者和政府在不同条件下的演化稳定策略,下面进一步分析相应演化结果并作出经济管理意义上的解释。 综上可知,当C0>Pn-Pr-z(T+S)且C0>y(Pn-Pr)时,三方博弈系统最终演化到(0,1,0),演化稳定策略为(不伪装,购买,不检查),即销售商选择不伪装策略,消费者选择购买策略,政府选择不检查策略。此时,市场达到有效配置,销售商、消费者和政府选择Nash均衡策略,保证了三方的收益。注意到y和z是变量,要使三方系统最终演化到(0,1,0),需满足C0>max{Pn-Pr-0·(T+S),1·(Pn-Pr)}即C0>Pn-Pr。这与未考虑政府干预时的销售商和消费者双方博弈的结果相同,即只能通过影响销售商伪装成本C0来促进市场向有效状态发展,政府并没有发挥作用。 结合命题2和命题3可知,(0,1,1)在任何条件下都不是演化稳定策略,即策略组合(不伪装,购买,检查)在任何条件下都不是三方博弈的演化稳定策略。在不考虑政府收益的情形下,观察销售商和消费者双方博弈的演化稳定策略可得,当C0>Pn-Pr-z(T+S)时,销售商选择不伪装策略且消费者选择购买策略,市场达到有效状态,故如果政府想要推进再制品市场向有效状态发展,就必须牺牲自身的利益。由于新产品零售价Pn和再制品零售价Pr是由市场决定的,难以改变其大小,而伪装成本C0属于不可控参数,故可以提高z,T和S以满足C0>Pn-Pr-z(T+S),使得市场向有效状态发展。在再制品市场发展的初期,存在的主要问题是市场经济发展和道德建设之间的矛盾,此时政府的规制措施显得尤为重要。所以,政府应该大范围大概率地检查再制品市场,并提高奖励和惩罚力度,这样有利于推动市场向有效状态发展。近年来,国家高度重视再制造产业发展,只有解决后端销售环节的价格欺骗问题,才可以为再制造产业保驾护航,实现再制造产业的良性发展。 在三方演化博弈模型中,为了说明政府的调控作用,下面采用数值算例来分析不同参数设置对演化结果的影响。 (1)设Pn=80,Pr=60,Vr=90,C0=19,T=2,C1=2,S=2,z=0.5。易知,C0>Pn-Pr-z(T+S)且C0 图1 C0>Pn-Pr-z(T+S)且C0 故不考虑政府收益时,销售商和消费者的演化稳定策略为(不伪装,购买),与3.4节中的结论一致。 (2)改变(1)中z的值,令z=0.6,其他参数保持不变。易知C0>Pn-Pr-z(T+S)且C0 图2 z增大时x和y的演化路径 改变(1)中S的值,令S=3,其他参数保持不变。易知,C0>Pn-Pr-z(T+S)且C0 图3 S增大时x和y的演化路径 改变(1)中T的值,令T=3,其他参数保持不变。易知,C0>Pn-Pr-z(T+S)且C0 图4 T增大时x和y的演化路径 综上可知,政府提高检查再制品市场的概率,加大对销售商的奖励和惩罚力度,都会加速促进销售商选择不伪装策略。事实上,这是因为政府的检查和奖惩措施会直接影响销售商的收益。而消费者的收益取决于Vr和Pn的大小关系以及Vr和Pr的大小关系,与其他因素无关。由于参数设置中Vr>Pn,又由假设3知Vr>Pr,所以无论销售商是否选择伪装售卖再制品,消费者均选择购买策略。因此,改变参数z,T和S的值,不会影响y的收敛速度。 本文针对再制品市场中的价格欺骗问题,首先,建立由销售商和消费者组成的双方演化博弈,探讨双方行为策略选择的制约因素,以及市场向有效状态演化的路径依赖。其次,考虑到政府作为市场的监督者,可以对销售商采取奖励或惩罚措施,建立由销售商、消费者和政府组成的三方演化博弈,利用分步分析法求解并进行演化结果分析。最后,通过数值仿真分析不同参数对系统演化结果的影响,剖析市场向有效状态演化的机理,得出以下结论: 结论1在销售商和消费者的双方演化博弈中,可以通过提高伪装成本来促使系统演化到(不伪装,购买)。事实上,伪装成本的提高会导致销售商伪装售卖再制品的收益下降,若下降到低于售卖再制品的收益,销售商就没有伪装的必要,从而选择不伪装策略;而销售商选择不伪装策略,会促使消费者选择购买策略。最终双方演化到(不伪装,购买),市场达到有效状态,形成良性发展。 结论2在销售商、消费者和政府的三方演化博弈中,由于新产品和再制品的零售价是由市场决定的,而伪装成本C0属于不可控参数,所以只有通过提高政府检查再制品市场的概率,以及加大政府对销售商的奖励和惩罚力度,才能推动市场向有效状态发展。当政府的干预措施对市场的有效配置起到积极促进作用时,政府无法达到Nash均衡,说明政府为促进再制品市场的良性发展需要付出一定的代价。 本文对再制品市场中的销售商、消费者和政府进行演化博弈的建模、分析和数值验证,得出再制品市场向有效状态发展的条件,为政府的决策制定提供相关参考,也为再制品市场的发展提供重要指导。另外,本文的研究存在一些需要改进的地方。例如,数值分析是在纯模拟的情形下进行的,没有结合再制品市场的实际数据,可能会与现实场景有所出入。未来可以收集再制品市场的大数据,利用计量经济学和数据挖掘等方法进行实证分析,完善再制品市场相关参与者行为的研究。2 双方演化博弈模型的建立及分析
2.1 收益矩阵
2.2 双方演化博弈模型的建立

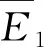
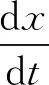
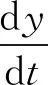
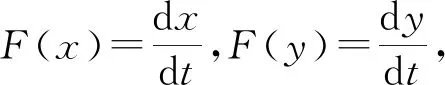
2.3 双方博弈演化稳定策略的求解
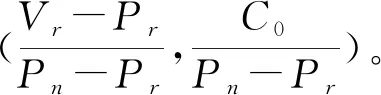

2.4 演化结果分析
3 三方演化博弈模型的建立及分析
3.1 收益矩阵


3.2 三方演化博弈模型的建立
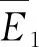
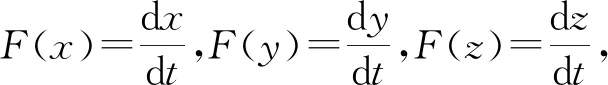
3.3 三方博弈演化稳定策略的求解
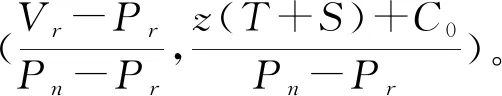

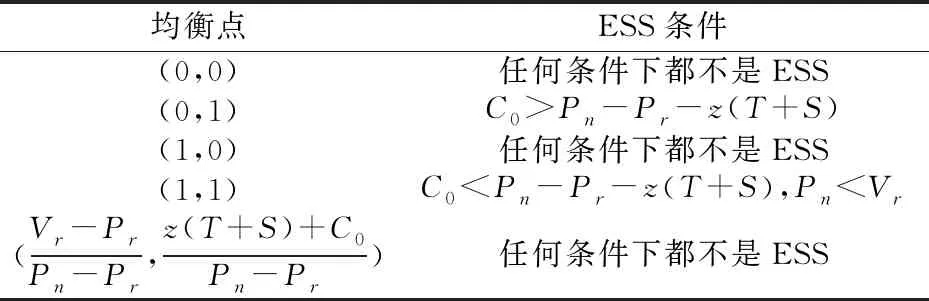
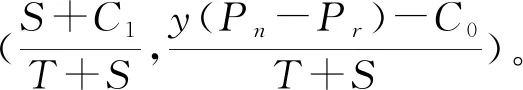
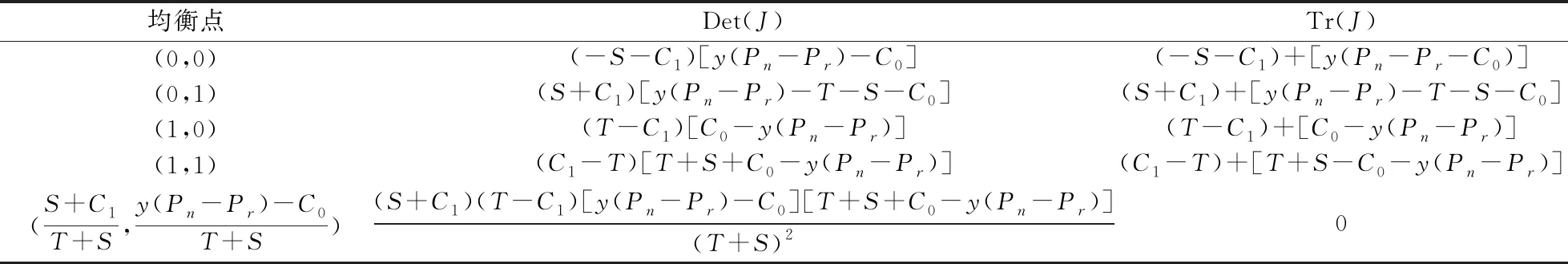
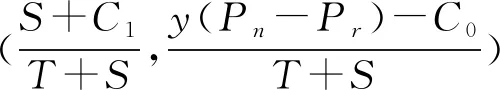
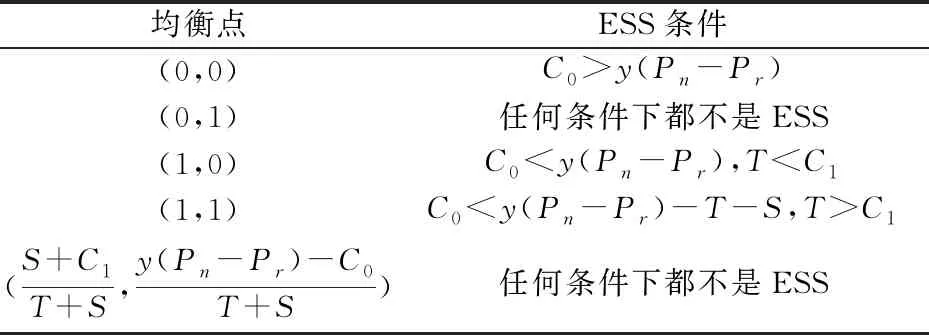
3.4 演化结果分析
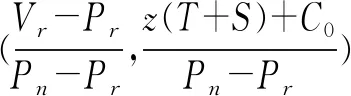
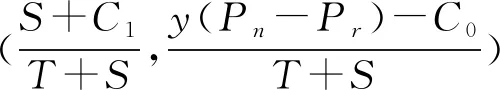
4 数值分析
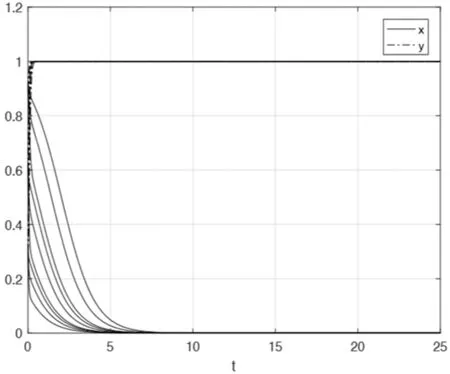
5 结论及建议

