数学焦虑影响数学概念知识加工的脑机制：静息态功能磁共振研究*

崔 芳 廖心明 杨嘉望 刘 洁

数学焦虑影响数学概念知识加工的脑机制：静息态功能磁共振研究*

崔 芳1廖心明2杨嘉望1刘 洁1

(1深圳大学心理学院, 深圳 518060) (2深圳市光明区玉律学校, 深圳 518107)

数学焦虑是一种对数学感到紧张焦虑的情绪反应。以往研究发现, 个体的数学焦虑水平越高, 在包括数学概念知识在内的不同类型数学任务中的表现就越差。本研究旨在探讨数学焦虑影响数学概念知识加工的脑机制。在控制广泛性焦虑的影响后, 筛选出92名健康成年人, 对其数学焦虑水平、语言理解能力、智力及其在数学概念知识任务中的表现进行了测量和分析。结果发现, 在控制了语言理解能力和智力的影响后, 个体的数学焦虑水平与其在数学概念知识任务中的成绩呈现显著负相关。对静息态功能磁共振数据的分析发现, 个体右侧水平段顶内沟与右侧脑岛之间的功能连接强度可以显著预测其数学概念知识成绩, 且该功能连接完全中介了数学焦虑水平与数学概念知识成绩之间的相关。这一结果表明, 数学/计算相关脑区(顶内沟)与焦虑相关脑区(脑岛)之间的相互作用可能是数学焦虑干扰数学概念知识任务的神经基础。

数学焦虑, 数学概念知识, 静息态功能磁共振, 顶内沟, 脑岛

1 引言

数学焦虑指个体在面对数字或与数学相关的情境时所体验到的恐惧、紧张、不安等负性情绪, 是一种有别于广泛性焦虑的特质水平的焦虑(Ashcraft, 2002; Ashcraft & Moore, 2009)。数学焦虑严重制约着个体发展。在生理层面, 当高数学焦虑个体准备进行数学任务时, 与威胁觉察(如扣带回皮层)和疼痛(如脑岛)相关的脑区活动显著增加(Lyons & Beilock, 2012); 在心理层面, 高数学焦虑人群对数学的感受与恐惧症类似, 这一强烈的负性情绪会侵占认知资源, 大大降低其在数学任务中的表现(Ashcraft et al., 1992; Lefevre et al., 2004)。为了避免再次体验这种负性情绪, 个体会出现行为上的回避倾向, 主动逃避数学相关情景(Pizzie & Kraemer, 2017), 如拒绝进行数学活动(如数字游戏、算术测验等) (Choe et al., 2019), 甚至可能影响其职业选择(Daker et al., 2021)。

高数学焦虑个体在预期或执行数学相关任务时表现出显著的神经活动异常。先前研究发现, 在高数学焦虑个体的大脑中, 与处理负性情绪相关的杏仁核(amygdala)激活会增强(Young et al., 2012); 与觉察威胁相关的扣带回皮层(cingulate cortex)和与疼痛感受相关的脑岛(insula)激活也会增强(Lyons & Beilock, 2012)。在负性情绪脑网络过度激活的同时, 与情绪调控相关的腹内侧前额叶(ventromedial prefrontal cortex, vMPFC)与杏仁核之间的连接在也显著增强(Young et al., 2012)。来自神经心理学及神经影像学的多项研究表明, 不同类型的数学加工任务均会激活双侧水平段顶内沟(horizontal intraparietal sulcus, HIPS) (Dehaene et al., 1999; Piazza et al., 2007; Santens et al., 2010)。而高数学焦虑个体在这些与数学加工相关的脑区, 如大脑双侧顶叶沟(Intraparietal Sulcus, IPS)和背外侧前额叶皮层(dorsal lateral prefrontal cortex, DLPFC)中的激活则显著减弱(Pizzie et al., 2020)。Young等人(2012)的研究也发现, 在进行数字计算时, 高数学焦虑儿童在IPS上的激活强度显著弱于对照组。

数学概念知识指数学领域内隐含或明确的原理或相互关系。关于计算关系的准则(包括加法、乘法交换律、结合律等)的算术原理就是一种数学概念知识。算术原理对儿童早期掌握基础运算起着至关重要的作用(Rittle-Johnson & Siegler, 1998; Rittle-Johnson et al., 2001)。数学概念知识本身具有抽象性及高度逻辑化的特征, 只有在理解并高度精炼的基础上才能形成概念知识结构。计算能力是指在熟练掌握各种数学概念知识的基础上所习得的数字操作能力(Maclellan, 2001)。概念知识是学习的基础, 也是知识的本质。只有在掌握基础的原理和定义后, 个体才能有效地进行数学运算。因此, 研究数学概念知识对理解数学认知加工具有重要意义。

先前研究表明, 数学焦虑水平与个体在数学概念知识任务中的表现存在显著负相关(Barroso et al., 2021; Hembree, 1990)。一项研究对中国香港316名6岁儿童进行了为期8个月的两次评估, 发现数学概念知识得分与数学焦虑水平呈显著负相关(Ching et al., 2020)。此外, 有研究指出, 对学生进行针对数学概念知识的补习够有效降低其数学焦虑水平(Khoule et al., 2017)。

尽管现有行为研究发现了数学焦虑与数学概念知识表现之间的关系, 而针对其神经机制的研究仍相对空白。神经机制层面的探讨能够帮助我们进一步理解数学焦虑影响数学表现的原因, 并为针对性地建立神经干预方案提供思路和证据。本研究拟采用静息态功能磁共振成像技术(resting-state functional Magnetic Resonance Imaging, rs-fMRI)探讨数学焦虑影响数学概念知识加工的神经机制。数学焦虑是一种领域特异性焦虑, 也是一种有别于广泛性焦虑的特质性焦虑(Kazelskis et al., 2001)。也就是说, 通过问卷测量的数学焦虑水平随着时间的推移相对稳定。大量研究指出, 静息状态下的血氧依赖性水平(blood oxygen level-dependent, BOLD)信号中的低频波动(< 0.1 Hz)与健康个体人格特征的变异性(di Martino et al., 2009; Oathes et al., 2015)和认知加工能力(如一般语义处理)相关(Xu et al., 2016)。据此, 本研究将利用rs-fMRI揭示数学焦虑与数学概念知识表现之间存在的神经关联。关于数学概念知识的神经影像学研究发现, 数学概念知识加工不仅激活了数学/视空间相关的脑区, 也激活了与一般语义加工相关的脑区, 如左侧额下回(Inferior frontal gyrus, IFG)和左侧颞中回(middle temporal gyrus, MTG) (Liu, 2017; 2019; Zhang et al., 2012)。本研究也将同时关注数学/视空间加工脑区和一般语义加工脑区在数学概念知识水平和数学焦虑的关系中所起的作用。

本研究将采用语言描述的算术原理测验任务来评估个体的数学概念知识掌握水平, 同时记录静息态下被试的大脑功能连接情况, 并分析其数学焦虑水平与数学概念知识任务表现之间的关系及其神经机制。研究假设为：行为层面上, 在控制广泛性焦虑水平、智力与语义理解能力的影响后, 数学焦虑仍然能够负向预测个体在数学概念知识任务中的表现; 神经层面上, 数学焦虑与数学概念知识加工的核心脑区及/或二者之间的功能连接可能与行为效应之间存在相关。

2 方法

2.1 被试

采用G-power软件(Faul et al., 2009)计算可知, 达到中等效应量(0.3)需要111个样本。计划样本量为111人。采用数学焦虑量表(shortened Mathematics Anxiety Rating Scale, sMARS, Alexander & Martray, 1989)及特质−状态焦虑量表(State-Trait Anxiety Inventory, STAI, Spielberger et al., 1983) 测量所招募人员的数学焦虑水平和广泛性焦虑水平。排除特质焦虑及状态焦虑异常(STAI总分 ≥ 100分)的11名个体后, 100名健康成年人被试参与了后续实验。根据rs-fMRI预处理结果, 排除8名头部旋转角度> 1.5°或平移距离 > 1.5 mm的被试后, 共92名被试数据纳入后续分析。年龄为18～23岁(= 20.91岁,= 2.33, 女性43人)。视力与矫正视力正常, 均为右利手, 无神经或精神障碍史。本研究依据《赫尔辛基宣言》的道德准则和原则进行, 经深圳大学医学院医学伦理委员会(伦理审核号：CBDCS202112140035)批准, 所有被试均签署知情同意书。

2.2 认知行为测验

本实验采用言语表达的算术原理测验评估个体的数学概念知识水平, 采用词汇语义测验和非语言矩阵推理测试测量个体的语义理解及智力水平。

2.2.1 算术原理测验

该测验用于评估个体对数学概念知识的理解与掌握, 主要包括5种基础的算术原理(交换律、结合律、减数法则、除法法则以及分步运算中去括号法则)。为避免由于数字呈现引起的数学焦虑带来额外影响, 采用言语表达的算术原理进行测验。例如, 呈现“交换加数的位置和不变”, 被试需要判断该句子是否正确, 若正确则按“Q”键, 错误则按“P”键(见图1A)。共40个试次, 被试需在3分钟内又快又准地作答。完成率及正确率越高, 得分越高。

2.2.2 词汇语义测验

该测验用于评估被试的语言理解能力, 以排除这一无关变量。每个试次中, 屏幕中会呈现一个不完整的句子, 被试需要从多个备选答案中选择合适的词填补语句空缺, 选择屏幕左侧的词按“Q”键, 选择右侧的词按“P”键(见图1B)。共120个试次, 被试需在5分钟内又快又准地作答。

2.2.3 非言语矩阵推理测验

该测验在瑞文标准渐进矩阵测验(1998)基础上改编而成, 用于评估个体的一般智力, 以排除这一无关变量。每个试次中, 屏幕中会呈现一个不完整的图片, 被试需要根据图片的内在规则, 在6～8个选项中选择适宜的图形来填补缺失的部分, 用鼠标进行点击选择(见图1C)。被试需在10分钟内又快又准地作答。

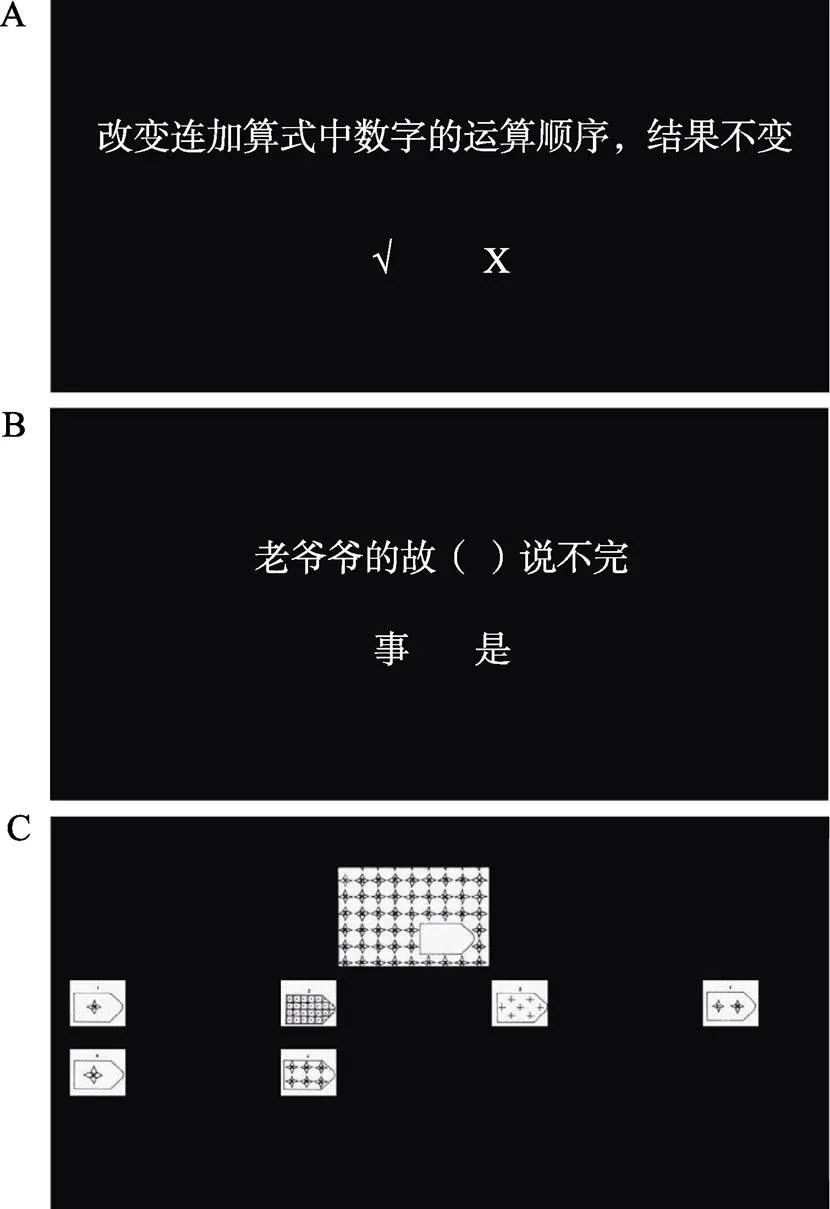
图1 认知行为测验示意图 (A)算术原理测验; (B)词汇语义测验; (C)非语言矩阵推理测验

2.3 实验流程

实验前, 被试在线上完成数学焦虑量表(sMARS)及特质−状态焦虑量表(STAI)。STAI得分不超过100分的被试参加认知行为测验和静息态磁共振扫描。认知行为测验包括言语表达的算术原理测验、词汇语义测试和非语言矩阵推理。行为测验由一名主试在安静的房间内监测被试在电脑上完成。被试的答案和反应时通过“在线心理实验系统(Online Psychological Experiment System, OPES)” (www.dweipsy.com/lattice)自动记录。在确保被试身体健康并符合核磁实验安全标准后, 被试在经过专业培训的扫描员陪同下, 进入核磁操作间闭眼完成静息态扫描。全程保持身体, 特别是头部静止。扫描时长约8分钟。

2.4 功能磁共振数据采集

静息态磁共振数据使用西门子Prisma 3.0T核磁共振仪器进行数据采集。采用梯度回波序列, 通过三维矢状T1加权磁化强度快速采集, 获得高分辨率结构图像, 参数为：重复时间(Repetition time, TR) = 2300 ms, 回波时间(Echo time, TE) = 2.26 ms,翻转角(flip angle) = 8°, 视场(field of view) = 232 mm × 256 mm, 获得矩阵(acquisition matrix) = 232 mm × 256 mm, 层厚(slice thickness) = 1 mm, 体素大小(voxel size) = 1 mm × 1 mm × 1 mm。采用梯度回波T2加权回波平面成像序列采集静息态功能图像, 具体参数为：重复时间 = 1500 ms, 回波时间 = 30 ms, 翻转角 = 70°, 视场 = 192 mm × 192 mm, 获得矩阵 = 94 mm × 94 mm。整个大脑划分为46层, 层厚3 mm, 体素大小 = 2.04 mm × 2.04 mm × 3 mm。

2.5 fMRI数据预处理

静息态fMRI数据使用DPABI软件(http://www. restfmri.net/forum/DPABI)进行预处理(Yan et al., 2016)。先将所有原始DICOM数据转换为NIFTI格式。结构像采用DARTEL方法分割为灰质、白质和脑积液。随后, 功能像采用如下步骤处理：1)删除前10个时间点的数据; 2)进行时间层校正(slice timing); 3)将结构像与功能像对齐; 4)进行空间标准化(spatial normalization), 空间标准化后体素为3 mm × 3 mm × 3 mm, 将图像配准到标准MNI (montreal neurological institute); 5)高斯平滑(smoothing) (平滑核[FWHW] = 6 mm); 6)进行去信号线性漂移(detrend); 7)去头动, 回归掉常用的混淆参数, 包括白质信号、脑积液信号(Fox et al., 2005)和24个头动参数(当前时间点的6个头动参数、前一个时间点的6个头动参数以及12个相应的平方项) (Friston et al., 1996; Yan et al., 2013); 8)带通滤波(band filter), 滤波范围为0.01～0.1 Hz。

2.6 数据分析

2.6.1 定义感兴趣脑区(Regions of Interest, ROI)

关于数学概念的脑成像研究发现, 相对于数字计算, 数学概念知识(如算术原理、数学术语)加工更依赖于语义/概念加工脑区(如左侧MTG和左侧眶部IFG); 而相对于一般语义加工, 数学概念知识加工则更依赖于视空间加工脑区(如IPS) (Liu et al., 2017; Zhang et al., 2012)。基于这些前期研究, 把语义的认知加工定位在左侧MTG和左侧眶部IFG, 空间/数量加工的脑区则选自一项视空间加工的元分析研究中显著激活的双侧水平段顶内沟(lHIPS与rHIPS) (Boccia et al., 2014)作为本研究的感兴趣区(坐标点及选取来源见表1与图2)。

表1 感兴趣脑区(ROI)信息

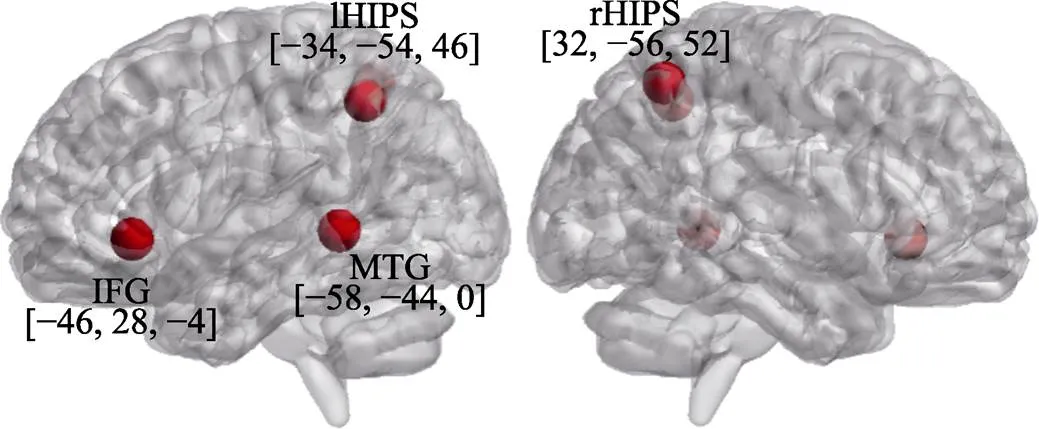
图2 四个感兴趣脑区(ROI)坐标位置示意图

2.6.2 基于种子点(Seed)的功能连接与行为数据的相关分析

以选定的4个ROI为功能网络分析的种子点, 绘制以种子点的MNI坐标为中心, 半径为6 mm的球体, 并计算每个被试的种子区和整个大脑之间其他区域的静息状态功能连接(Resting state functional imaging, rsFC)。控制一般智力得分和语言技能表现后, 对静息态影像与算术原理测验得分之间做偏相关分析。分别对每个ROI分别进行相同的分析。结果使用高斯随机场(Gaussian Random Field, GRF), 体素水平< 0.005, 且cluster水平< 0.0125 (校正前< 0.05)的阈值进行校正。

2.6.3 中介分析

为了探讨与算术原理加工相关的大脑功能连接在数学焦虑与算术原理任务表现之间关系中的作用, 将数学焦虑水平作为自变量, 算术原理表现为因变量。选择前述分析中rsFC与种子点的功能连接与算术原理表现显著相关的脑区, 并提取这些脑区的平均估计参数作为中介变量。Bootstrap方法不需要假设抽样的正态分布, 而是通过反复抽样来估计间接效应及其抽样分布, 并据此分布特征来估计间接效应的置信区间(CI)。本研究沿用了这一方法(Preacher & Hayes, 2008), 将Bootstrap再抽样设定为5000次运行中介效应检验。

3 结果

3.1 行为结果

三项认知测验得分结果, 包括各项测验的均值和标准差及每次测验的内部一致性(α)评分系数见表2。每项测验的内部一致性均在可接受范围(0.71～ 0.84)。数学焦虑与特质焦虑得分分别为67.39 ± 32.39和39.29 ± 8.41 [均值 ± 标准差]。从偏度、峰度及正态性检验(K-S检验)结果可知, 三项认知测验的得分服从正态分布。皮尔逊相关检验表明, 算术原理的表现与数学焦虑水平呈显著负相关(= −0.26,= 0.008), 在控制特质焦虑水平, 语言技能表现及一般智力得分后, 二者仍有显著负相关(= −0.29,= 0.004)。

3.2 fMRI结果

3.2.1 ROI选取的合理性验证

分别提取了每个ROI与另外的3个ROI之间的功能连接, 得到每个被试在4对ROI之间功能连接的值(共16条连接)。然后以平均框架方向位移(frame-wise displacement, FD)为控制变量, 将16条连接值分别与算术原理成绩做相关, 发现右侧HIPS与左侧MTG之间的功能连接强度与算术原理呈显著正相关(未校正< 0.001)。具体来说, 当以HIPS为种子点时, 二者之间的FC与算术原理成绩相关显著(= 0.35,< 0.001); 以左侧MTG为种子点时, 二者之间的FC与算术原理成绩的相关显著(= 0.34,< 0.001)。上述结果经过FDR校正后仍显著。这一结果表明, 本研究所选取的ROI与算术原理的加工之间的确存在关联。

表2 认知测验的描述性统计

3.2.2 基于种子点的功能连接性预测行为表现

在控制一般智力测验和语言理解成绩的情况下, 分别计算双侧HIPS、左侧IFG和左侧MTG为种子区的功能连接图与算术原理得分之间的偏相关图。Cluster水平校正后, 仅发现以右侧HIPS为种子点时, 右侧脑岛(峰值点MNI [45, 3, −12],= −0.41, cluster size = 368)与算术原理成绩呈显著负相关。对4个ROI结果采用了体素水平< 0.005, cluster水平< 0.0125 (< 0.05未校正)的阈值进行多重比较校正。结果保持一致：即仅有以右侧HIPS为种子点进行相关时, 得到一个显著的cluster (峰值点MNI [45, 3, −12],= −0.41, cluster size = 368) (见图3)。

此外, 分别计算了双侧HIPS、左侧IFG和左侧MTG为种子区的功能连接图与数学焦虑水平之间的相关图。结果发现：在以双侧HIPS、左侧MTG为种子点的功能连接图与数学焦虑均无显著相关, 以左侧眶部IFG与右侧顶枕交界处(峰值MNI [33, −66, 45],= 0.43, cluster size = 230)的功能连接强度与数学焦虑水平呈显著正相关。对四个ROI的结果采用体素水平< 0.005, cluster水平< 0.0125 (< 0.05未校正)的阈值进行多重比较校正, 校正后结果仍一致。

3.2.3 中介分析

在右侧HIPS为种子点的功能连接图中, 提取每个被试右脑岛的平均估计参数, 并将其作为中介变量。结果表明, 右脑岛与右侧HIPS之间功能连接强度在数学焦虑水平与算术原理的表现之间具有显著的中介作用。正态理论检验显示a路径显著(= 2.18,= 0.032), b路径显著(= −4.75,< 0.001)。当加入中介变量后, 显著的c路径(= −2.63,= 0.009)变得不显著(= −1.79,= 0.076)。即使在控制了平均框架方向位移(frame-wise displacement, FD)后, 中介效应仍然显著：正态理论检验显示a路径显著(= 2.03,= 0.046), b路径显著(= −4.28,< 0.001)。加入中介变量后, 之前显著的c路径(= −2.47,= 0.015)不再显著(= −1.74,= 0.085) (见图4)。

为了消除重复验证的影响, 尝试进行了全脑voxel水平的中介分析。使用Wager等(2008, 2009)开发的工具包“Mediation toolbox”, 以数学焦虑水平为自变量X, 算术原理的成绩为因变量Y, 右侧HIPS为种子点的功能连接图为中介变量M, 做单水平中介分析(Single level mediation analysis)。FDR校正的阈限下未发现显著的结果。将阈限降低为未校正< 0.01时, 发现一个位于右侧脑岛的cluster (峰值MNI坐标[45, 0, 3], cluster size = 297, 统计量 = 6.91)。该结果虽然未在全脑水平达到较强的统计显著性, 但也从另一方面验证和补充了研究的可信度。此外, 为了进一步探究该作用来自于数学焦虑还是广泛性焦虑, 将特质焦虑作为自变量放入了中介模型, 结果发现c路径不显著(= −0.071,= 0.481)。表明特质焦虑与算术原理之间不存在显著负相关。

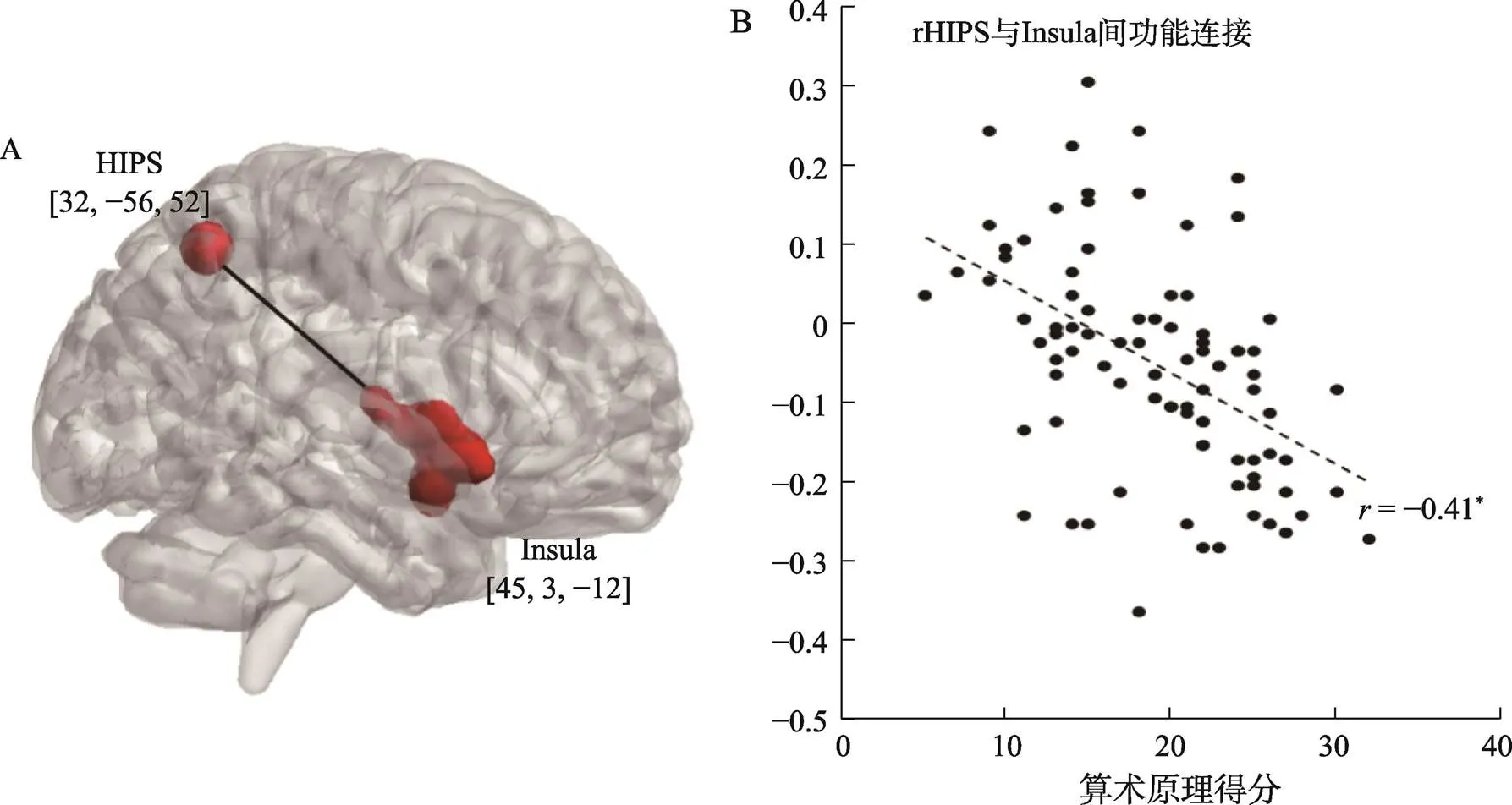
图3 fMRI结果示意图(A)右侧脑岛与右侧HIPS存在显著功能连接; (B)脑岛与右侧HIPS之间的功能连接与算术原理得分相关

图4 中介分析结果

由于在功能连接图与数学焦虑水平的相关分析中发现了以左侧眶部IFG为种子点到顶枕交界处的功能连接与数学焦虑水平存在显著相关, 因而我们进一步验证了这条功能连接是否能作为中介变量。在左侧眶部IFG为种子点的功能连接图中, 提取每个被试顶枕交界处的平均估计参数, 并将其作为中介变量, 以数学焦虑水平为自变量, 以算术原理表现为因变量进行中介效应分析。结果表明, 左侧眶额下回IFG与右侧顶枕交界处之间的功能连接强度在数学焦虑水平与算术原理之间的中介作用不显著。

4 讨论

本研究采用言语表达的算术原理测验考察了不同数学焦虑个体的数学概念知识掌握情况, 并结合静息态功能磁共振探讨了数学焦虑与数学概念知识表现之间的关系及其相关的神经机制, 以帮助我们更好地理解了数学焦虑与数学任务表现之间的关系。行为层面上的结果与前人的研究一致, 证实了数学焦虑能够负向预测个体在数学概念知识任务中的表现。在神经层面上, 发现负责数学/视空间加工的右侧HIPS与焦虑情绪相关的脑区右侧脑岛之间的功能连接强度完全中介了数学焦虑水平与数学概念知识表现之间的关系。表明数学/计算脑区(HIPS)与焦虑脑区构成的神经回路可能是数学焦虑影响数学概念知识表征的重要神经通路。本研究还发现, 在数学概念知识任务的加工中, 负责一般语义加工的脑区与算术原理成绩之间不存在相关性, 与数学焦虑得分也不相关。右侧HIPS为种子点的功能连接图中未发现与数学焦虑水平在全脑水平上的相关, 这可能是由于数学焦虑水平对静息态功能连接来说特异性较高, 而全脑水平的校正对信号强度的要求高, 因此难以在全脑水平出现阳性结果, 这一推测在全脑水平中介分析的结果中进一步得到了验证, 即中介效应在FDR校正的阈限下未达到显著, 而未校正< 0.01的阈限下可以在全脑水平验证HIPS-脑岛通路与数学焦虑水平的相关关系, 及其在算术原理成绩与数学焦虑之间的中介作用。

以往关于对于数学焦虑情绪唤醒的研究通常关注杏仁核。例如, 有研究发现高数学焦虑个体在完成数字计算任务时, 杏仁核被异常激活, 且杏仁核与背外侧前额叶(DLPFC)之间的功能连接也显著降低(Pizzie et al., 2020; Young et al., 2012)。值得注意的是, 脑岛也被普遍认为是焦虑情绪的关键脑区(Bishop, 2007; Paulus & Stein, 2006; Somerville et al., 2013)。焦虑包含两个重要的组成成分, 一是交感神经被过度激活导致强烈的生理反应, 二是担忧带来的持续增加的心理负担。先前研究提出, 情绪可能需要通过脑岛对身体内在生理感受的觉知来获得并维持焦虑, 从而增强焦虑体验(Hartley & Phelps, 2012; Paulus & Stein, 2006)。同时, 焦虑障碍中过度或不恰当的情绪反应可能是源于脑岛——前额叶系统的调节失败导致的(Bishop, 2009; Kim & Whalen, 2009)。本研究中发现的高数学焦虑个体右侧脑岛与HIPS之间的功能连接异常, 可能是由于脑岛对强烈的焦虑感知异常以及过度担忧占据了个体完成算术原理任务的认知资源。

大脑顶内沟(IPS)被广泛认为是具有核心数量感知表征系统, 并涉及数值与数学问题的解决的重要脑区(Ansari et al., 2006; Cohen Kadosh et al., 2005; Eger et al., 2003; Nieder & Dehaene, 2009; Pinel et al., 2001), 以往的研究也印证了数值处理与数学概念知识的处理都将激活双侧的HIPS (Liu et al., 2017)。本研究采用的言语表达的数学概念知识测验虽然不直接涉及数字, 但是与数字计算后的数量关系有关, 被试需要运算描述的计算公式并判断是否正确, 这可能是大脑在HIPS的自发神经活动的功能连接与算术原理存在相关的原因, 我们推测高数学焦虑人群在算术原理加工是HIPS的激活可能会减弱。先前一项任务态fMRI研究也发现, 数学焦虑水平较高个体的HIPS激活水平显著较低数学焦虑个体相比更低, 且杏仁核与HIPS之间的功能连接较弱(Young et al., 2012), 这与本研究的发现具有一致性。表明数学焦虑程度高的人在加工数学知识时在数学特异性的功能脑区上存在缺陷。此外, 由于前人研究中左侧额下回和左侧颞中回也参与了算术原理的加工(Liu et al., 2017, 2019)。当种子区位于这两个区域时, 我们的结果没有发现任何相关性, 这意味着数学焦虑人群受损的脑功能局限于数字加工领域, 而不涉及一般语义加工的脑功能。

关于HIPS的作用, 还有一种解释是其主要负责自上而下的注意力控制, 而不是数学/视空间加工相关的脑区。IPS是额顶神经网络中负责认知控制的一个关键的脑区(Dosenbach et al., 2008; Sylvester et al., 2012)。fMRI研究表明, 高特质焦虑的个体在额顶网络中的激活减弱(Bishop, 2009), 并且其相关的功能连通性也存在异常(Basten et al., 2011)。Etkin等人在2009年的一项研究中发现, 广泛性焦虑障碍患者的额顶叶网络与杏仁核区域之间的功能连接显著增强(Etkin et al., 2009)。对于数学焦虑水平较高的人群而言, HIPS与脑岛之间功能连接的变化可能是由于自上而下的注意力控制异常导致的, 而不是由于他们在数学方面存在缺陷。然而, 关于这一解释的合理性与有效性还需要后续更深一步的研究探讨。目前两种可能的研究解释都印证了数学焦虑水平与数学概念知识表现会导致脑岛与HIPS之间功能连接强度变化存在一致性。

除了考察数学焦虑分别作用于脑岛以及双侧HIPS影响之外, 本研究还计算出右脑岛与右侧HIPS之间功能连接强度大小, 并以此为中介再次分析语言算术原理测验的表现与数学焦虑的关系。结果发现右侧脑岛与右侧HIPS之间的功能连接随着数学概念知识表现的提高而降低, 这表明两个脑区之间的功能连接可能会影响数学的加工效率。除此之外, 随着数学焦虑水平的增高, 两者之间的功能连接强度也随之加强, 说明更高的数学焦虑可能会导致右侧脑岛与右侧HIPS之间的过度联系。因此未来可以以脑岛与HIPS之间功能连接这一方向进行进一步的探究, 以解释数学焦虑与数学表现之间的因果关系。

本研究存在几点局限性。首先, 除了脑岛, 杏仁核也被认为是焦虑回路中关键的大脑区域。先前两项任务态功能核磁共振成像研究发现, 高水平数学焦虑被试在执行算数任务时, 杏仁核的激活增加(Pizzie et al., 2020; Young et al., 2012)。然而, 我们未能在本数据中发现这一区域的活动变化。研究者应谨慎考虑当前结果, 并在将来的研究中进一步验证杏仁核的作用。其次, 本研究仅考察了不同数学焦虑被试在静息态功能成像时的功能连接, 而任务态的功能核磁成像实验则是未来研究关注的方向之一。第三, 对于HIPS的功能解释并不单一。例如, HIPS的异常激活可能与自上而下的注意控制障碍有关(Dosenbach et al., 2008; Sylvester et al., 2012)。因此, 未来需要考虑一种新的设计来排除由焦虑引起的注意缺陷的可能性, 以进一步探讨和澄清当前结果。

随着脑神经科学的发展与应用, 探查大脑神经机制可以为人们的行为表现提供实证证据, 在应用层面上也可以考虑采用脑神经科学的方法精准干预相关脑区, 以达到缓解数学焦虑或矫治数学学习障碍的作用。先前一项经颅直流电刺激(transcranial direct current stimulation, tDCS)研究对负责情绪调节的左背外侧前额叶皮层进行兴奋性刺激, 成功地提高了数学焦虑被试在进行简单算术决策时的反应时间, 并大大降低了代表个体生理应激唤醒的皮质醇的浓度(Sarkar et al., 2014), 为干预数学焦虑提供了新的方向与方案。基于当前发现, 即数学焦虑水平越高的个体, 其右侧HIPS和同侧脑岛之间的功能连接越强。我们有理由推测, 通过对位于皮层上的右侧HIPS区域施加神经调控(如经颅电刺激、经颅磁刺激等), 可能通过这条神经通路降低右侧脑岛的激活程度, 从而减轻数学焦虑, 提高数学表现。近年来, 国家布局了系列重大脑科学项目, 青少年脑智开发是其中重要的需求; 二十大又提出教育强国的战略目标。本研究揭示了数学焦虑对算术原理表现影响的脑机制, 提示情绪对学科成绩的影响可能通过大脑中数学加工脑区HIPS与负性情绪加工脑区脑岛通路起作用, 为高数学焦虑的青少年在数学学习相关的脑智发育中提供了神经调控的思路, 也为帮助儿童青少年解决学习困难问题提供了新的干预靶点。

Alexander, L., & Martray, C. (1989). The development of an abbreviated version of the mathematics anxiety rating scale.t,(3), 143−150.

Ansari, D., Fugelsang, J. A., Dhital, B., & Venkatraman, V. (2006). Dissociating response conflict from numerical magnitude processing in the brain: An event-related fMRI study.,(2), 799−805.

Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences.(5), 181−185.

Ashcraft, M. H., Donley, R. D., Halas, M. A., & Vakali, M. (1992). Working memory, automaticity, and problem difficulty.InJ. I. D. Campbell (Ed.),(pp. 301–329). North-Holland.

Ashcraft, M. H., & Moore, A. M. (2009). Mathematics anxiety and the affective drop in performance.,(3), 197−205.

Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A., & Daucourt, M. C. (2021). A meta-analysis of the relation between math anxiety and math achievement.,(2), 134−168.

Basten, U., Stelzel, C., & Fiebach, C. J. (2011). Trait anxiety modulates the neural efficiency of inhibitory control.(10), 3132−3145.

Binder, J. R., Desai, R. H., Graves, W. W., & Conant, L. L. (2009). Where is the semantic system? A critical review and meta-analysis of 120 functional neuroimaging studies.,(12), 2767−2796.

Bishop, S. J. (2007). Neurocognitive mechanisms of anxiety: An integrative account.,(7), 307−316.

Bishop, S. J. (2009). Trait anxiety and impoverished prefrontal control of attention.,(1), 92−98.

Boccia, M., Nemmi, F., & Guariglia, C. (2014). Neuropsychology of environmental navigation in humans: Review and meta-analysis of FMRI studies in healthy participants.,(2), 236−251.

Ching, B. H. H., Kong, K. H. C., Wu, H. X., & Chen, T. T. (2020). Examining the reciprocal relations of mathematics anxiety to quantitative reasoning and number knowledge in Chinese children.,, 101919.

Choe, K. W., Jenifer, J. B., Rozek, C. S., Berman, M. G., & Beilock, S. L. (2019). Calculated avoidance: Math anxiety predicts math avoidance in effort-based decision-making.,(11), eaay1062.

Cohen Kadosh, R., Henik, A., Rubinsten, O., Mohr, H., Dori, H., van de Ven, V., … Linden, D. E. (2005). Are numbers special?: The comparison systems of the human brain investigated by fMRI.(9), 1238−1248.

Daker, R. J., Gattas, S. U., Sokolowski, H. M., Green, A. E., & Lyons, I. M. (2021). First-year students’ math anxiety predicts STEM avoidance and underperformance throughoutuniversity, independently of math ability.(1), 1−13.

Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., & Tsivkin, S. (1999). Sources of mathematical thinking: Behavioral and brain-imaging evidence.,(5416), 970−974.

di Martino, A., Ross, K., Uddin, L. Q., Sklar, A. B., Castellanos, F. X., & Milham, M. P. (2009). Functional brain correlates of social and nonsocial processes in autism spectrum disorders: An activation likelihood estimation meta-analysis.y,(1), 63−74.

Dosenbach, N. U., Fair, D. A., Cohen, A. L., Schlaggar, B. L., & Petersen, S. E. (2008). A dual-networks architecture of top-down control.,(3), 99−105.

Eger, E., Sterzer, P., Russ, M. O., Giraud, A. L., & Kleinschmidt, A. (2003). A supramodal number representation in human intraparietal cortex.,(4), 719−726.

Etkin, A., Prater, K. E., Schatzberg, A. F., Menon, V., & Greicius, M. D. (2009). Disrupted amygdalar subregion functional connectivity and evidence of a compensatory network in generalized anxiety disorder.,(12), 1361−1372.

Faul, F., Erdfelder, E., Buchner, A., & Lang, A. G. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses.,(4), 1149−1160.

Friston, K. J., Williams, S., Howard, R., Frackowiak, R. S., & Turner, R. (1996). Movement-related effects in fMRI time- series.,(3), 346−355.

Hartley, C. A., & Phelps, E. A. (2012). Anxiety and decision- making.,(2), 113−118.

Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety.,(1), 33−46

Kazelskis, R., Reeves, C., Kersh, M. E., Bailey, G., Cole, K., Larmon, M., Hall, L., & Holliday, D. C. (2001). Mathematics anxiety and test anxiety: Separate constructs?,(2), 137−146.

Khoule, A., Bonsu, N. O., & El Houari, H. (2017). Impact of conceptual and procedural knowledge on students mathematics anxiety.,(1), 8−17.

Kim, M. J., & Whalen, P. J. (2009). The structural integrity of an amygdala-prefrontal pathway predicts trait anxiety.(37), 11614−11618.

LeFevre, J. A., DeStefano, D., Coleman, B., & Shanahan, T. (2004). Mathematical cognition and working memory. InJ. I. D. Campbell (Ed.),(pp. 361–377). Psychology Press, New York.

Liu, J., Yuan, L., Chen, C., Cui, J., Zhang, H., & Zhou, X. (2019). The semantic system supports the processing of mathematical principles.,, 102−118.

Liu, J., Zhang, H., Chen, C., Chen, H., Cui, J., & Zhou, X. (2017). The neural circuits for arithmetic principles.,, 432−446.

Lyons, I. M., & Beilock, S. L. (2012). When math hurts: Math anxiety predicts pain network activation in anticipation of doing math.,(10), e48076.

Maclellan, E. (2001). Mental calculation: Its place in the development of numeracy.,(2), 145−154.

Nieder, A., & Dehaene, S. (2009). Representation of number in the brain.,185−208.

Oathes, D. J., Patenaude, B., Schatzberg, A. F., & Etkin, A. (2015). Neurobiological signatures of anxiety and depression in resting-state functional magnetic resonance imaging.,(4), 385−393.

Paulus, M. P., & Stein, M. B. (2006). An insular view of anxiety.,(4), 383−387.

Piazza, M., Pinel, P., Le Bihan, D., & Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex.,(2), 293−305.

Pinel, P., Dehaene, S., Riviere, D., & LeBihan, D. (2001). Modulation of parietal activation by semantic distance in a number comparison task.,(5), 1013−1026.

Pizzie, R. G., & Kraemer, D. J. (2017). Avoiding math on a rapid timescale: Emotional responsivity and anxious attention in math anxiety.,, 100−107.

Pizzie, R. G., Raman, N., & Kraemer, D. J. (2020). Math anxiety and executive function: Neural influences of task switching on arithmetic processing.,(2), 309−325.

Preacher, K. J., & Hayes, A. F. (2008). Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models.,(3), 879−891.

Rittle-Johnson, B., & Siegler, R. S. (1998). The relation between conceptual and procedural knowledge in learning mathematics: A review. In C. Donlan (Ed.),(pp. 75−110). Psychology Press/Taylor & Francis (UK).

Rittle-Johnson, B., Siegler, R. S., & Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: An iterative process.,(2), 346−362.

Santens, S., Roggeman, C., Fias, W., & Verguts, T. (2010). Number processing pathways in human parietal cortex.,(1), 77−88.

Sarkar, A., Dowker, A., & Kadosh, R. C. (2014). Cognitive enhancement or cognitive cost: Trait-specific outcomes of brain stimulation in the case of mathematics anxiety.,(50), 16605−16610.

Somerville, L. H., Wagner, D. D., Wig, G. S., Moran, J. M., Whalen, P. J., & Kelley, W. M. (2013). Interactions between transient and sustained neural signals support the generation and regulation of anxious emotion.,(1), 49−60.

Spielberger, C. D., Gorsuch, R. L., Lushene, R., Vagg, P. R., & Jacobs, G. A. (1983).. Palo Alto, CA: Consulting Psychologists Press.

Sylvester, C. M., Corbetta, M., Raichle, M. E., Rodebaugh, T. L., Schlaggar, B. L., Sheline, Y. I., ... Lenze, E. J. (2012). Functional network dysfunction in anxiety and anxiety disorders.,(9), 527−535.

Wager, T. D., Davidson, M. L., Hughes, B. L., Lindquist, M. A., & Ochsner, K. N. (2008). Prefrontal-subcortical pathways mediating successful emotion regulation.,(6), 1037−1050.

Wager, T. D., Waugh, C. E., Lindquist, M., Noll, D. C., Fredrickson, B. L., & Taylor, S. F. (2009). Brain mediators of cardiovascular responses to social threat: Part I: Reciprocal dorsal and ventral sub-regions of the medial prefrontal cortex and heart-rate reactivity.,(3), 821−835.

Wu, C. Y., Ho, M. H. R., & Chen, S. H. A. (2012). A meta-analysis of fMRI studies on Chinese orthographic, phonological, and semantic processing.,(1), 381−391.

Xu, Y., Lin, Q., Han, Z., He, Y., & Bi, Y. (2016). Intrinsic functional network architecture of human semantic processing: Modules and hubs.e,, 542−555.

Yan, C. G., Craddock, R. C., Zuo, X. N., Zang, Y. F., & Milham, M. P. (2013). Standardizing the intrinsic brain: Towards robust measurement of inter-individual variation in 1000 functional connectomes.,, 246−262.

Yan, C. G., Wang, X. D., Zuo, X. N., & Zang, Y. F. (2016). DPABI: Data processing & analysis for (resting-state) brain imaging.s,(3), 339−351.

Young, C. B., Wu, S. S., & Menon, V. (2012). The neurodevelopmental basis of math anxiety.,(5), 492−501.

Zhang, H., Chen, C., & Zhou, X. (2012). Neural correlates of numbers and mathematical terms.,(1), 230−240.

The neural mechanism of the impact of mathematical anxiety on the math conceptual knowledge: Evidence from a resting-state fMRI study

CUI Fang1, LIAO Xinming2, YANG Jiawang1, LIU Jie1

(1School of Psychology, Shenzhen University, Shenzhen 518060, China) (2Shen Zhen Guangming Yulv School, Shenzhen 518107, China)

Math, the basic tool for technology and engineering, is fundamental to professionals in Science, Technology, Engineering, and Math (STEM) fields. Math anxiety is a negative emotional response that is characterized by avoidance and feelings of stress and anxiety in situations involving mathematical reasoning. Math anxiety in students has been suggested to dampening learning and mastering of mathematics.

Among various math skills, the ability to do conceptual knowledge of math has been confirmed to be significantly and negatively correlated with math anxiety. As an essential type of knowledge in mathematics, conceptual understanding is defined as an implicit or explicit understanding of the principles that govern a domain and of the relationships between units of knowledge in a domain. Neuroimaging studies have shown that the regions of the brain needed for processing mathematical conceptual knowledge might differ from those needed for other types of math such as calculation or basic numerical processing. Doing conceptual knowledge of math reportedly activated brain regions that are related to numerical processing, such as the bilateral intraparietal sulcus (IPS), as well as brain regions associated with general conceptual knowledge processing, such as the left inferior frontal gyrus (IFG) and left middle temporal gyrus (MTG).

Although the correlation between conceptual math skill and math anxiety has been confirmed at the behavioral level, the neural mechanism remains unknown. Previous studies found that in people with high math anxiety, brain regions related to negative emotions were found to be more active during the numerical tasks, while regions related to emotion regulation and the processing of numbers and calculations were less active. In addition to hyper-activation of the emotional network, brain regions that govern mathematical tasks, showed reduced activation in people with high math anxiety.

To address the neural mechanism that allows math anxiety to impede the processing of conceptual math, we used resting-state functional magnetic resonance imaging (fMRI) to determine how brain activity is related to the effects that math anxiety has on the performance of problems that test conceptual math knowledge. (1) we selected four regions of interest (ROIs) that were considered as important neural substrates for processing arithmetic principles in a previous fMRI study. We performed correlation analysis between the seed-based FC maps and the performance of math conceptual knowledge to construct neural pathways that process math conceptual knowledge. (2) we utilized mediation analysis to investigate the relationships between math anxiety, the performance of math conceptual knowledge, and the possible neural pathways. To avoid numerical formats that would likely induce confounding math anxiety, we used a verbalized arithmetic principles task.

After excluding trait anxiety and state anxiety abnormalities, as well as participants who exceed the criterion of head motion during scanning, 92 healthy adult university students (43 females), aged 18-23 years (= 20.91,= 2.33) were left for the data analysis. After controlling for the extraneous factors such as language and intelligence, the partial correlation results showed a significant negative correlation between mathematical anxiety and performance on conceptual knowledge of mathematics (= −0.26,= 0.008), which replicated the findings of previous studies and confirmed that mathematical anxiety did inhibit individuals' learning and acquisition of conceptual knowledge of mathematics. The functional connectivity in the resting brain of individuals was correlated with different levels of mathematical anxiety in the functional connectivity between the horizontal segment of the right intraparietal sulcus and the right insula. Furthermore, this functional connectivity fully mediated the correlation between the level of mathematical anxiety and the performance of mathematical conceptual knowledge. These results suggest that the interaction between mathematical/computation-related brain regions (e.g. the horizontal segment of the intraparietal sulcus) and anxiety circuits (e.g. the insula) may be the neural basis for the negative effect of mathematical anxiety on the performance of mathematical conceptual knowledge.

mathematical anxiety, mathematical concept knowledge, resting-state fMRI, intraparietal sulcus, insula

2022-06-16

* 深圳市稳定支持计划(20200803154243023), 国家自然科学基金(31900779, 32171013)和深港脑科学创新研究院(2023SHIBS0003)资助。

B849: G44

刘洁, E-mail: ljier06@gmail.com