旋转部件热套紧量选取及仿真验证

肖 雷

（东方电气集团东方电机有限公司，四川 德阳 618000）

1 旋转部件离心力分析

1.1 集电环套筒离心应力和位移

集电环也称滑环，是同步电机的关键部件之一，与刷架、电刷、转子绕组和轴配合完成同步电机转子电能的输入，并提供转子旋转磁场。目前的同步电机集电环普遍为集电环套筒整体套装在轴上，然后在集电环套筒上包扎、固化绝缘，加工后将集电环套装到包有绝缘的集电环套筒上。其中，集电环、绝缘套筒和转轴之间都是典型的过盈配合结构，即热套结构。

该文以某同步电动机集电环套筒为例，并在超速工况下计算、讨论旋转部件热套紧量的选取问题。其中集电环套筒材料为Q235 钢，轴材料为高质量合金钢。集电环套筒外形如图1 所示，具体尺寸见表1。

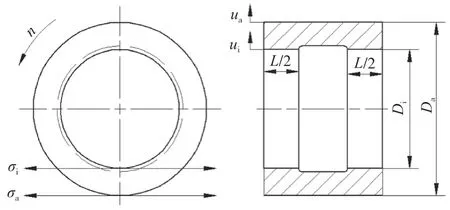
图1 集电环套筒

表1 集电环套筒数据

集电环套筒承受离心力时的计算如公式（1）～公式（3）所示。

集电环套筒外圆表面径向位移如公式（5）所示。

集电环套筒内圆表面切应力如公式（6）所示。

从公式（1）到公式（7）可以看出，旋转部件应力、位移仅与材料密度和转速有关，与热套接触长度无关，即增大热套接触尺寸不能改善集电环套筒热套强度。热套长度会影响传递力矩的大小及拆卸难度，后文将详细论述。

在集电环套筒内圆确定的情况下，k越大，内圆与外圆尺寸越相近，内外圆应力、位移也越接近，材料的利用率也就越高。考虑既要满足材料应力要求，又要提高材料利用率，一般取k＞0.6，部分大型电机甚至取k＞0.8。

由于接触尺寸长度与圆环强度无关，因此取集电环套筒部分切面进行有限元分析，计算结果见表2。

表2 集电环套计算结果与仿真结果对比

1.2 与集电环配合的轴面离心应力和位移

与集电环套筒离心力应力和位移计算方法相同。与集电环配合的轴如图2 所示。

图2 与集电环配合的轴

轴外圆表面切应力及外表面径向位移如公式（8）、公式（9）所示。

公式（8）～公式（9）的计算结果与仿真结果对比见表3。

表3 轴计算结果与仿真合应力结果对比

1.3 最小过盈量

采用温差法进行装配时，配合表面微观不平度被擦平得较少，可忽略不计，因此单边最小实际过盈量如公式（10）所示。

采用压入法进行装配时，配合表面微观不平度的波峰总会被擦伤或压平一部分，压平部分通常取两配合表面粗糙度RZ的60%，即在半径上增加0.6（Rzi+Rzo），因此单边最小实际过盈量如公式（11）所示。

该例中，集电环套筒与轴之间采用热套装配，因此最终集电环套筒配合面取ø170H7（+0.040），轴配合面取ø170r6（+0.093+0.068），单边最小过盈量δmin为（1.4×10-3）cm，单边最大过盈量δmax为（4.65×10-3）cm。

2 热套后应力分析

热套结束后，集电环套筒与轴之间的相互作用力如图3 所示，配合面为最大过盈量时的接触压力如公式（12）所示。

图3 过盈配合

该公式仅适用于转轴为实心的情况。

集电环套筒配合面切向应力如公式（13）所示。

轴配合面切向应力如公式（14）所示。

式中：负号代表压应力。

同理可求得最小过盈量切径向应力，见表4。

表4 热套后应力（单位：kg/cm2）

过盈配合仿真模型及应力结果如图4 所示。图4 的仿真是基于内应力的仿真，取的是集电环套筒及轴部分切面，仿真结果和理论结果相差不大。现实中由于边界的存在，因此结果会有所差异。

图4 过盈配合仿真模型及应力结果

在实际工程应用中，为了降低拆装难度，会采取集电环套筒与轴两端配合且中间不接触的设计。这种结构在装配完成后，在配合面和非配合面的交界处会出现应力集中的情况。配合长度越长，配合段中部的压强值越接近理论计算值。配合长度越小，应力集中峰值就越大，其变化规律近似于线性关系。配合长度越短，配合段内的接触压力平均值就越高。

该文所讲示例的最小过盈量、最大过盈量仿真结果见表5、表6。其中接触压力是作用在接触面上的作用力与反作用力，因此套筒配合面与轴配合面接触压力本应相等。由于集电环套筒中间段不与轴配合，接触面上应力分布不均，存在由接触引起的边缘应力集中，因此仿真结果中套筒配合面与轴配合面的平均接触压力出现了差别。

表5 最小过盈量仿真结果（接触面平均值）

表6 最大过盈量仿真结果（接触面平均值）

另外从有限元仿真可以看出，集电环套筒和轴的过盈联接存在边缘效应，边缘应力的值大大高于弹性力学的解。基于弹性力学理论获得的应力结果没有考虑集电环套筒接触边缘的变化引起的应力集中，具有一定的局限性，特别是寿命计算会与实际情况偏差较大。弹性力学获得的解析解只能与有限元的平均值进行比较。目前经典力学尚无法求解包容件边缘应力的变化，而边缘应力集中将直接影响联接的强度和寿命。解析法与有限元法应结合使用，才是精确分析集电环套筒的应力及疲劳的有效方法。

如果集电环套筒边缘应力集中系数较大，应采取开卸载槽的措施，减少应力集中，并提高联接的可靠性和疲劳寿命。

3 集电环套筒装配

温差装配法是利用材料热胀冷缩的性能加热包容件或冷却被包容件，或二者同时进行的方法。配合件在温差条件下失去过盈量，从而实现自由装配，待温差消失后即形成紧配合[1]。装配温度计算如公式（15）所示。

式中：t为装配时包容件加热温度；t0为环境温度；δ为实测最大过盈量；δ0为热套单边最小间隙，取0.1mm；α为包容件线涨系数；dk为包容件线内径。

4 集电环套筒拆卸

过盈联接的装配方法按原理不同可分为压入法、胀缩法和油压法[2]。不同的装压方法摩擦系数不同，导致拆装力也不同。由于影响摩擦系数的因素较多，如联接件材料、装配方式、润滑油、粗糙度和过盈量等，因此会导致摩擦系数变化范围很宽，获得精确摩擦系数的难度也较大。在非精准计算的情况下，不同材料过盈联接接触面摩擦系数见表7。

过盈联接件因本身结构特性，拆卸时存在较大困难，工作表面易被划伤，甚至因无法拆卸而只能破坏性拆除。拆卸集电环套筒时一般使用千斤顶。如果千斤顶就位，集电环套筒仍无松动迹象，需要加热集电环套筒。但加热时间不得太长，不得让热传至主轴。拆卸时需要的最大压出应力（最大过盈量）如公式（16）所示。

式中：L为有效配合面长度，单位cm。

拆卸时需要的最小压出应力（最小过盈量）如公式（17）所示。

该文所讲示例的拆卸力见表8、表9。

表8 最大过盈量时集电环套筒拆卸力

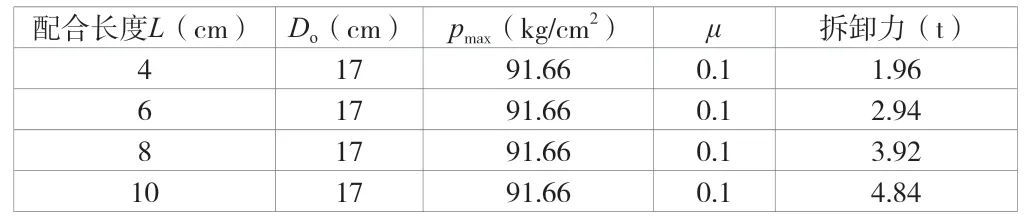
表9 最小过盈量时集电环套筒拆卸力

从表8、表9 可以看出，配合长度L虽与集电环套筒应力无关，但对集电环套筒的拆卸有极大影响。

真实模型有限元仿真结果如图5 所示。从图5 可以看出，集电环套筒及配合轴面应力主要集中在配合面边线上，两边线之间部分较小，所以配合长度L的取值不需要很大。

图5 真实模型仿真应力

5 转递载荷所需最小接触压力

过盈部件仅传递轴向力Fa时所需的最小接触压力如公式（18）所示。

过盈部件仅传递力矩M时所需的最小接触压力如公式（19）所示。

过盈部件同时传递轴向力Fa和力矩M时所需的最小接触压力如公式（20）所示。

从公式（18）～公式（20）可以看出，接触长度L在极大程度上会影响过盈部件传递力及力矩的大小。集电环套筒设计时还需要考虑所装配的集电环力矩的大小。

6 结语

该文通过解析法和有限元法，以集电环套筒热套紧量的选取为例，介绍了旋转部件离心力的计算、热套紧量的选取、配合面应力计算、拆卸力以及传递载荷等情况，为旋转部件热套尺寸的选取提出了建议。该文通过解析法和有限元法对比，得出经典力学求解的理论值只能与有限元的平局值相对应的结论，经典力学在处理边缘效应上具有一定的局限性。可以将经典力学的结果作为设计参考，同时还需要配合有限元法核算应力和疲劳。在应力集中系数较大的情况下，需要开卸载槽来缓解应力集中。另外，温度分布不均匀会影响过盈量大小，零件内部产生热应力、工作环境温度过高、装配温度间有差异、材料线弹性系数不同也会影响过盈联接的性能。该文例子中集电环套筒材料与轴材料线胀系数相差不大，因此热应力的影响可以忽略。