汽轮发电机集电环机械设计计算

李 德，李志和，兰 波，刘继慧，李海龙

(1. 哈尔滨电机厂有限责任公司，黑龙江哈尔滨 150040；2. 哈尔滨大电机研究所，黑龙江哈尔滨 150040)

0 引言

集电环也称滑环，是汽轮发电机关键部件之一，其与电刷、转子绕组配合，起到提供电机旋转磁场的作用。现今汽轮发电机集电环普遍采用通过绝缘套筒整体套装在轴上的结构方式，集电环、绝缘套筒与转轴之间为典型过盈配合。发电机运行时，集电环既承受热套过盈配合力的作用，同时又承受旋转离心力的作用，受力情形较为复杂，故准确计算集电环机械应力对其结构设计具有重要的指导意义。资料显示：熊东旭[1]对集电环的内外径、轴向尺寸与材质，绝缘套筒厚度及配合紧量，集电环螺旋沟尺寸等问题给出设计建议；王迪等[2]基于有限元理论，采用ANSYS Workbench对1 000 MW汽轮发电机集电环装配应力进行了三维仿真分析；汪耕等[3]就汽轮发电机集电环的材质、套装工艺、冷却方式、电腐蚀等问题进行过深刻讨论，在进行汽轮发电机集电环设计时还应关注和避免集电环和电刷在发电机运行过程中的各类故障；史德利等[4]曾针对300 MW汽轮发电机集电环与电刷磨损发热问题改进优化了相关结构；李贤明等[5]对发电机运行中电刷和集电环常见故障和处理方法也进行了系统的介绍。

本文基于经典弹性力学理论对汽轮发电机集电环、绝缘套筒与转轴过盈配合变形协调方程进行了推导，计算了静止、额定、超速三种工况下的集电环应力与分离转速，并与ANSYS Workbench非线性接触仿真结果进行对比，以验证本文所推导的集电环机械设计计算方法的有效性。

1 集电环装配变形协调方程推导

1.1 集电环装配结构简化

汽轮发电机典型的转轴-绝缘套筒-集电环装配结构剖面见图1。集电环包含正负两环，由高质量合金钢制成，热套在经绝缘处理的套筒上。为保证有效通风冷却和去除粉尘，集电环外表面开有螺旋形沟槽，内部开有轴向、斜向通风孔，且常在两个集电环之间的轴上安装风扇装置，以降低由励磁电流引起的温升。

图1 集电环装配结构示意

在汽轮发电机运行状态下，集电环既承受自身旋转的机械离心力、又承受过盈配合力的作用。本文对集电环机械计算进行推导时不计集电环表面螺旋沟槽与通风孔的影响，将集电环装配简化为圆筒式结构，简化后的转轴-绝缘套筒-集电环装配结构见图2。图中，Li为绝缘套筒长度，Lc为集电环长度，D0为转轴内径，Dsi为转轴与绝缘套筒配合直径，Dic为绝缘套筒与集电环配合直径，Dc为集电环外径。各部件材料属性见表1。

表1 集电环装配材料属性

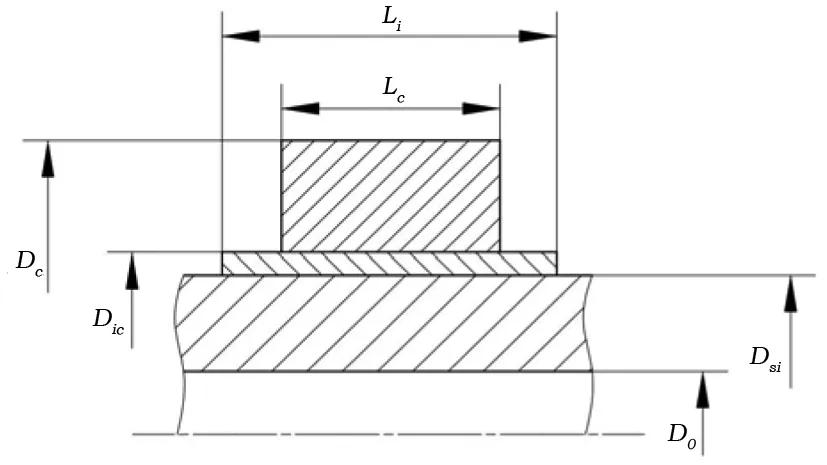
图2 集电环装配结构简化

集电环热套安装完成后，转轴可视作承受外压作用的圆筒模型，集电环可视作承受内压作用的圆筒模型，而绝缘套筒则可视作同时承受内压和外压作用的圆筒模型。基于弹性力学理论[6]，内半径为a，外半径为b的圆筒承受内压Pi和外压Pe时的位移表达式为：

(1)

内半径为a，外半径为b的等厚圆盘旋转工况下的位移表达式为：

(2)

式中：ω为角速度；a≤r≤b。

联立式(1)、式(2)可推导出转轴、绝缘套筒、集电环承受过盈配合及机械旋转作用下的变形和柔度。

1.2 集电环装配变形和柔度推导

由1.1节可知，考虑集电环承受内压P1情况，令Pi=P1，Pe=0，a=Dic/2，b=Dc/2，代入式(1)，则集电环内径变形量为：

(3)

(4)

式中：Q1为集电环与绝缘套筒配合力。

根据柔度定义，可求得集电环柔度为：

(5)

考虑集电环以角速度ω旋转时，令a=Dic/2，b=Dc/2，代入式(2)，则其内径变形量为：

(6)

同理，也可推导出转轴与绝缘套筒的变形及柔度表达式。为简化书写格式及便于计算，现引入如下无量纲系数：

(7)

(8)

令转速n=1 000 r/min，将表1材料属性代入式(5)、式(6)，整理，可求得集电环柔度为：

(9)

集电环变形系数为：

(10)

内径处配合力引起绝缘套筒内径柔度为：

(11)

外径处配合力引起绝缘套筒内径柔度为：

(12)

内径处配合力引起绝缘套筒外径柔度为：

(13)

外径处配合力引起绝缘套筒外径柔度为：

(14)

绝缘套筒外径变形系数为：

(15)

绝缘套筒内径变形系数为：

(16)

转轴柔度为：

(17)

式中：ξ为考虑转轴外伸端对柔度影响而进行修正的系数。

转轴变形系数为：

(18)

根据式(10)、(15)、(16)、(18)，可进行集电环装配配合紧量的初步计算及选取，集电环与绝缘套筒之间配合紧量初值计算公式为：

(19)

(20)

式中：np为超速转速。

在进行紧量设计时，需综合考虑集电环装配的应力及变形问题，既要保证各种工况下集电环应力满足强度要求，又要保证在超速工况下集电环装配各部件不发生脱离或松动。

1.3 集电环装配变形协调方程

综上，根据集电环装配受载及接触变形情况，获得集电环装配变形协调方程为：

(21)

式中：Q1为集电环与绝缘套筒配合力；Q2为绝缘套筒与转轴配合力；δci为集电环与绝缘套筒之间的设计紧量；δis为绝缘套筒与转轴之间的设计紧量。

方程(21)为二元一次线性方程组，其表征了集电环装配受热套过盈及旋转离心力作用下的变形关系。根据方程(21)，求解配合力Q1、Q2，从而计算集电环内径位置的环向应力为：

(22)

由式(22)可看出，式中右边第一项为热套配合作用产生的应力分量，第二项则为旋转机械作用引起的应力分量。

根据方程组(21)，亦可求得在设计紧量状态下转轴-绝缘套筒-集电环的分离转速，令Q1=0，消元，求得绝缘套筒与转轴分离转速表达式为：

同理，令Q2=0，消元，求得集电环与绝缘套筒分离转速表达式为：

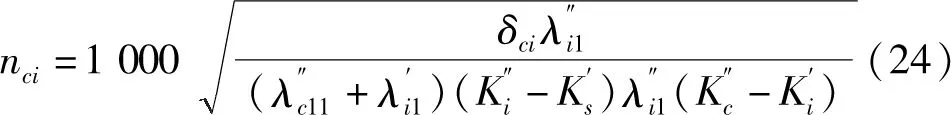
2 算例及有效性验证

基于本文推导的集电环机械设计计算方法，选取某一产品发电机集电环轴段作为算例，计算该集电环在静止、额定、超速三种工况下的最大环向应力及分离转速。为验证该计算方法的有效性，采用ANSYS Workbench建立了集电环装配二维接触轴对称模型，集电环与绝缘套筒、绝缘套筒与转轴之间施加相应的接触设计紧量，并约束转轴端面轴向位移。对于分离转速的仿真，是通过渐进式提高转速，观测模型的接触压力分布状态来判断，当接触压力接近于0时可认为接触失效，集电环装配发生分离。有限元仿真结果应力平均值为集电环内径位置的路径应力，理论计算和有限元仿真结果见表2。静止、额定、超速三种工况下集电环装配环向应力及径向位移分布见图3、图4。

图3 集电环装配环向应力分布

图4 集电环装配径向位移分布

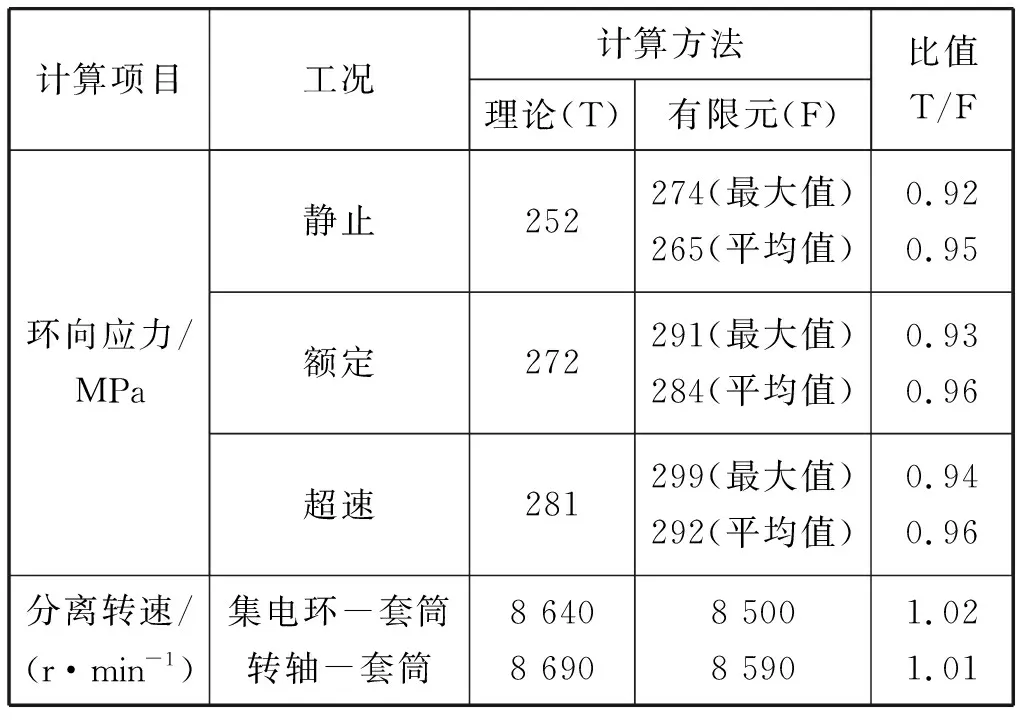
表2 集电环装配计算结果汇总

由表2可知，集电环装配理论计算与有限元仿真结果吻合较好，表明了本文推导的集电环机械设计计算方法的有效性，集电环最大环向拉应力位于集电环内径位置。有限元仿真应力普遍高于理论计算结果，其原因在于有限元仿真可有效模拟因刚度差异引起的绝缘套筒径向变形的不均匀性，这种变形不均匀性使得集电环最大环向拉应力位置出现在集电环内径端部，这是理论计算所不能计及的。与有限元方法相比，本文推导的集电环理论计算方法更为高效和便捷，特别适用于集电环结构初步设计阶段。

3 结论

基于经典弹性力学理论，本文系统地推导了汽轮发电机集电环机械设计计算过程并计算了不同工况下的集电环机械应力及分离转速。研究表明：集电环机械设计理论计算与ANSYS Workbench有限元接触非线性仿真结果吻合较好，本文推导的理论计算方法可有效用于汽轮发电机集电环的机械设计。