快速反射镜理论建模与仿真分析

谢 娜，杜言鲁，姜世洲，巩全成，王明超，徐飞飞，王新伟，齐 媛

（西安应用光学研究所，陕西 西安 710065）

引言

作为精密控制光束指向的光学器件——快速反射镜（fast steering mirror,FSM）具有体积小、响应速度快、位置精度高等优点，通常与大惯量跟踪框架构成复合轴系统，用于校正主轴系统的跟踪偏差，以及抑制由基座、大气等干扰引起的视轴抖动，广泛应用于激光通信、激光武器、自适应光学等对瞄准线有高精度指向与稳定要求的领域[1-5]。

建立包含结构特性的FSM 控制系统模型，分析结构特性与控制系统间的相互作用，对于指导FSM 设计具有重要意义。目前，FSM 设计大多采用机电分离的设计方法，无法开展结构特性和伺服控制系统共同作用下FSM 性能分析。文献[6]对FSM 柔性支承传动结构进行了介绍，并对柔顺传动单元空间构型、刚度分析以及FSM 动力学分析方法等进行了归纳；文献[7]通过运动学分析，根据约束和各个自由度间的空间关系，确定挠性支承的约束和自由度模型；文献[8～10]采用理论建模或有限元分析方法对柔性铰链结构特性进行了分析，并基于多目标优化提出了柔性铰链结构设计方法。文献[11～14]对FSM 控制系统进行建模和仿真，开展了自适应鲁棒控制、滑模动态面控制以及基于状态空间的现代控制方法研究。文献[15～18]通过动力学分析，建立了包含结构特性的控制系统仿真模型，但仅考虑了工作轴转动刚度，未能分析柔性铰链非工作轴刚度特性和负载质心偏离柔性铰链支承中心等对FSM 性能的影响。

本文结合在研的两轴快速反射镜，将柔性铰链结构简化为弹性环节，基于动力学分析建立FSM的运动微分方程，基于传递函数理论推导出被控对象和基座扰动隔离的传递函数，并以此为基础搭建包含结构特性的FSM 控制系统仿真模型，分析负载质心偏离柔性铰链支承中心、结构谐振频率等对控制系统性能的影响，从而指导FSM 设计。

1 FSM 组成及工作原理

以音圈电机驱动的两轴FSM 为例，由基座、柔性铰链、反射镜、音圈电机、角度测量传感器和驱动控制系统组成，如图1 所示。反射镜、反射镜支撑结构、音圈电机线圈部分构成负载，反射镜支撑结构与音圈电机线圈部分直接连接，音圈电机磁钢以及角度传感器安装在基座上，通过柔性铰链将负载与基座相连。通过音圈电机推拉，使反射镜发生角度偏转，采用角度测量传感器（如电涡流位移传感器）对角度进行测量，反馈给驱动控制系统，实现FSM 的闭环控制。

图1 两轴FSM 结构组成Fig.1 Structural composition diagram of two degrees of freedom FSM

2 FSM 理论建模

2.1 FSM 动力学模型

作为FSM 的关键部件，柔性铰链为反射镜负载运动分配各个方向自由度，以两轴FSM 为例，柔性铰链允许绕2 个工作轴转动，限制3 个轴平动自由度和1 个非工作轴的转动自由度。对两轴FSM进行简化，如图2 所示。图2（a）为正视图，建立坐标系o-xyz，o为柔性铰链旋转中心，x轴垂直纸面向外，通过音圈电机V1、V2 推（拉）与音圈电机V3、V4 拉（推）实现绕x轴转动，音圈电机V1、V2与音圈电机V3、V4 在y轴方向的间距为 2b，通过电涡流传感器S2、S4 差分解算得到绕x轴的旋转角度。图2（b）为左视图，y轴垂直于纸面向里，通过音圈电机V2、V3 推（拉）与音圈电机V1、V4 拉（推）实现绕y轴转动，音圈电机V2、V3 与音圈电机V1、V4 在x轴方向的间距为 2a，通过电涡流传感器S1、S3 差分解算得到绕y轴的旋转角度。

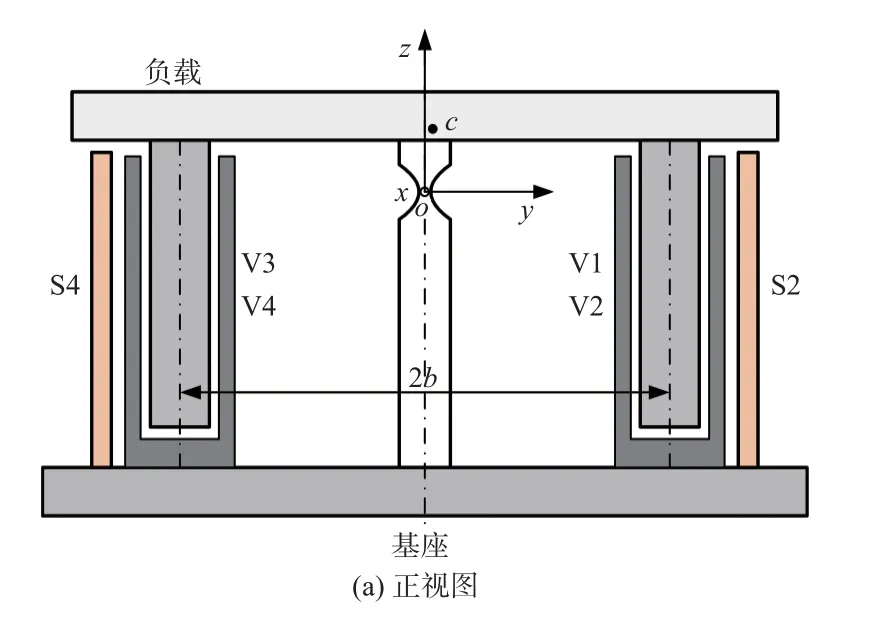
图2 两轴FSM 简化模型Fig.2 Simplified model of two degrees of freedom FSM

将柔性铰链简化为弹性环节，即等效为3 个轴平动刚度kx、ky、kz和3 个轴转动刚度kα、kβ、kγ，对应各自由度方向的结构阻尼系数分别为cx、cy、cz、cα、cβ、cγ，可描述柔性铰链的结构特性。由于结构设计、加工和安装误差等，负载质心c不可避免地偏离柔性铰链的转动中心，设偏离位移为(Δx,Δy,Δz)T。

设负载质量为m，在建立坐标系o-xyz下，负载绕x轴的转动惯量为Ixx，负载绕y轴的转动惯量为Iyy。

设基座的平动位移为(xi,yi,zi)T，基座的转动角位移为(αi,βi,γi)T，反射镜负载在柔性铰链转动中心处的平动位移为(xo,yo,zo)T，转动角位移为(αo,βo,γo)T，反射镜负载的运动可看作是平动位移(xo,yo,zo)T和转动角位移(αo,βo,γo)T的复合运动。其中负载相对基座的转动角位移为 α、β，α=αo-αi，β=βo-βi，可由角度传感器测量得到。

反射镜负载相对基座运动，柔性铰链产生的弹性力为

反射镜负载质心偏离转动中心，产生的绕转动中心的不平衡力矩为

反射镜负载相对基座转动，柔性铰链产生的转动力矩为

音圈电机动子与反射镜支撑结构直接相连，音圈电机施加到反射镜负载上的作用力、转动力矩分别为

式中：FV1、FV2、FV3、FV4为音圈电机V1～V4 在z轴方向产生的驱动力，沿z轴方向为正，反之为负。由于FSM 驱动通常采用推拉方式，各音圈电机在z轴方向的合力为零。

基于上述动力学分析，可得反射镜负载平移运动(xo,yo,zo)T的运动微分方程为

反射镜负载绕o点转动的运动微分方程为

当负载质心偏离柔性铰链转动中心的位置Δx=Δy=Δz=0时，转动的运动微分方程为

此时基座的线运动不会耦合出反射镜负载的角运动。

选用结构固有频率（平动固有频率、转动固有频率）来表征柔性铰链的结构特性。由式（6）可得柔性铰链的无阻尼平动固有频率（定义为非工作轴固有频率）为

由式（8）可得柔性铰链绕x轴、y轴的无阻尼转动固有频率（定义为工作轴固有频率）为

在柔性铰链结构设计时，允许绕2 个工作轴转动（绕x轴和绕y轴转动），即要求frx、fry较小，同时限制非工作轴方向的自由度，即要求fnx、fny、fnz远大于frx、fry，且越大越好。z轴为反射镜镜面的法线方向，绕z轴的转动不改变光束指向，但为了减少各自由度运动耦合，要求在绕z轴的转动方向上应具有大的刚度。

2.2 被控对象传递函数

音圈电机作为驱动元件，具有精度高、频率响应快等特点，音圈电机结构如图3（a）所示。线圈绕组置于永磁体磁场中，当线圈绕组中电流为i时，线圈受到的安培力为Kti（Kt为电机力矩系数），与永磁体的磁感应强度、每匝线圈在磁场中的有效长度、线圈匝数等有关。安培力的方向根据电流方向和磁场方向由左手定则确定，因此可通过改变电流的大小和方向控制音圈电机输出力的大小和方向。

图3 音圈电机简化模型Fig.3 Simplified model of voice coil motor

图3（b）为音圈电机的等效电路图。假设音圈电机的电阻为Rv、电感为Lv、反电动势系数为Ke、电机力矩系数为Kt，根据基尔霍夫定律可得各个音圈电机的电压平衡方程：

式中：k=1,2,3,4；zk为音圈电机动子的线位移。各个音圈电机的输出力为

基于极小范数法对控制解耦，各个音圈电机的控制电压Uk与两转动轴控制电压Uα、Uβ间的关系为

在不考虑基座扰动的情况下，绕x轴、绕y轴的动力学方程分别为

将式（11）～式（13）代入式（14）和式（15）中，并对方程进行拉普拉斯变化，经代数运算后得到传递函数：

考虑到音圈电机电感较小，舍去分母中的三次项，此时传递函数变为

式中：ωrα、ωrβ为增加音圈电机模型后绕x轴和绕y轴转动方向的谐振频率；ξα、ξβ分别为对应的阻尼比，即：

2.3 基座扰动隔离传递函数

在仅考虑柔性铰链结构特性，控制系统不工作（即音圈电机输出力为0）情况下，负载转动的运动微分方程为

对式（6）和式（20）进行拉普拉斯变化，经代数运算后可得对基座上线加速度扰动ax、ay、az的隔离传递函数分别为

由上式可知，基座上沿x轴的线运动不会耦合出反射镜负载绕x轴 的转动，沿y轴方向的线运动不会耦合出反射镜负载绕y轴的转动。当负载质心偏离柔性铰链转动中心时，沿y轴、z轴的线运动会耦合出反射镜负载绕x轴的转动，其特性分别与柔性铰链绕x轴 的转动固有频率、沿y轴和z轴的平动固有频率有关。沿x轴、z轴的线运动会耦合出反射镜负载绕y轴的转动，其特性分别与柔性铰链绕y轴的转动固有频率、沿x轴和z轴的平动固有频率有关。

对基座上角速率扰动 ωx、ωy、ωz的隔离传递函数分别为

由此可知，反射镜负载绕x轴的转动仅由基座上绕x轴的角扰动引起，与基座上绕y轴、z轴的角扰动无关。反射镜负载绕y轴的转动仅由基座上绕y轴的角扰动引起，与基座上绕x轴、z轴的角扰动无关。其对基座角扰动隔离特性与绕x轴和y轴的转动固有频率有关。

3 FSM 仿真分析

3.1 FSM 仿真模型

根据上述建立的FSM 动力学方程和音圈电机理论模型，并增加音圈电机驱动器、角度传感器、控制器、以及基座扰动等仿真模型，搭建了FSM的全系统 Matlab/Simulink 仿真模型，如图4 所示。

图4 FSM 仿真模型Fig.4 Simulation model of FSM

3.2 结构固有频率对被控对象特性影响分析

在音圈电机选定的情况下，分析柔性铰链不同结构固有频率对被控对象特性的影响。以绕x轴转动为例，以控制电压Uα为输入，负载相对基座绕x轴的转角 α为输出，得到被控对象的幅频特性和相频特性曲线，如图5 所示。从图5 可以看出，在音圈电机参数确定情况下，随着转动固有频率的增加，阻尼比 ξα减小；当转动固有频率较小时，系统为过阻尼系统（ξα＞1），幅频特性曲线不会出现谐振峰；当转动固有频率较大时，系统为欠阻尼系统（ξα＜1），幅频特性曲线会出现谐振峰。

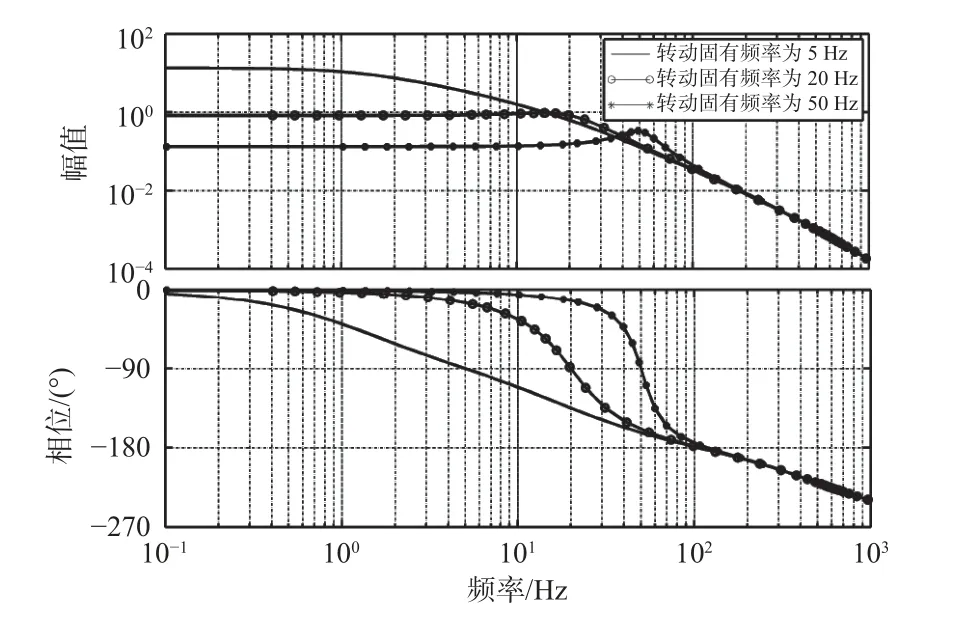
图5 被控对象伯德图Fig.5 Bode diagram of controlled object

当反射镜负载质心偏离柔性铰链支承中心时，基座上的线运动会耦合为反射镜负载的角运动，分析不同结构固有频率下，被控对象对线加速度运动的扰动隔离性能。根据实际加工的柔性铰链模态测试结果，设定工作轴固有频率为5 Hz、20 Hz和50 Hz，设定非工作轴的固有频率为300 Hz、600 Hz和900 Hz。以工作轴固有频率为5 Hz、20 Hz、50 Hz，非工作轴固有频率为300 Hz 为例，绘制了其对基座线加速度扰动的隔离曲线，如图6（a）所示。从图6（a）可以看出，随着转动固有频率（或工作轴固有频率）的增加，对基座低频区域线加速度扰动的隔离性能提升了，在转动固有频率（50 Hz）附近隔振性能稍有降低，在非工作轴固有频率处存在谐振峰，对高频区域扰动的隔离性能不变。以工作轴固有频率为20 Hz，非工作轴固有频率为300 Hz、600 Hz、900 Hz 为例，绘制了其对基座线加速度扰动的隔离曲线，如图6（b）所示。从图6（b）可以看出，对低频区域扰动的隔离性能基本一致，但随着非工作轴固有频率的增加，在非工作轴固有频率处谐振峰值下降。

快速反射镜基座上也存在角扰动，分析不同转动固有频率下，被控对象对基座角速率运动的扰动隔离性能。以工作轴固有频率为5 Hz、20 Hz、50 Hz，非工作轴固有频率为300 Hz 为例，绘制了其对基座角速率扰动的隔离曲线，如图7（a）所示。从图7（a）可以看出，随着转动固有频率的增加，对低频区域扰动的隔离性能提升了，在转动频率附近隔振性能稍有降低，对高频区域的隔离性能保持不变，且在非工作轴固有频率处未出现谐振峰。以工作轴固有频率为20 Hz，非工作轴固有频率为300 Hz、600 Hz、900 Hz 为例，绘制了其对基座角速率扰动的隔离曲线，如图7（b）所示。从图7（b）可以看出，改变非工作轴固有频率，对基座角速率扰动的隔离曲线保持不变，说明非工作轴固有频率对基座角扰动隔离性能无影响。

图7 不同结构固有频率下对角速率扰动隔离曲线Fig.7 Rejection curves for angular rate disturbance with different structural natural frequency

3.3 结构固有频率对FSM 控制性能影响分析

假定FSM 的工作轴固有频率为5 Hz，非工作轴固有频率为300 Hz，控制器采用经典PID 控制，经PID 参数整定后，控制系统的开环传递函数和闭环传递函数如图8 所示。从图8 可知，系统增益交界频率为300 Hz，相位裕度为60°；相位交界频率为421 Hz，增益裕量为40.1 dB；系统的闭环带宽(-3 dB)为480 Hz。

保持控制器参数不变，非工作轴固有频率为300 Hz，改变FSM 工作轴转动固有频率，得到系统的闭环传递函数曲线，如图9 所示。从图9 可以看出，随着转动固有频率的增加，系统的控制性能变差，转动固有频率越小，对控制性能越有利。以对10 Hz 指令信号跟踪为例，如图10 所示，工作轴固有频率为50 Hz 时，输出信号的幅值为指令信号的80%，跟踪偏差较大，主要由转动固有频率较大时系统为欠阻尼系统引起的。引入速度反馈对谐振峰值进行抑制，闭环传递函数曲线如图11 所示。从图11 可以看出，速度反馈可提升FSM 控制性能。

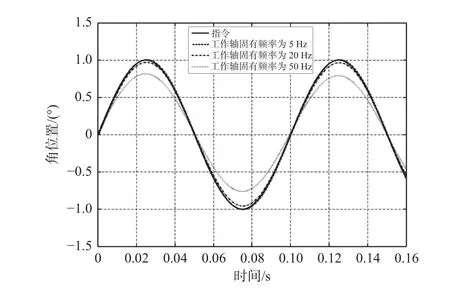
图10 对10Hz 正弦指令跟踪曲线Fig.10 Tracking curves to 10 Hz sine command

图11 含速率反馈FSM 控制系统传递曲线Fig.11 Transfer curves of FSM control system with rate feedback

在FSM 闭环控制下，分析反射镜基座线运动隔离性能。以工作轴固有频率为5 Hz、20 Hz、50 Hz，非工作轴固有频率为300 Hz 为例，绘制了FSM 闭环控制系统对基座线加速度扰动的隔离曲线，如图12（a）所示。从图12（a）可以看出，随着转动固有频率（或工作轴固有频率）的增加，对基座低频区域线加速度扰动的隔离性能有提升，在非工作轴固有频率处存在谐振峰。以工作轴固有频率为20 Hz，非工作轴固有频率为300 Hz、600 Hz、900 Hz为例，绘制了FSM 闭环控制系统对基座线加速度扰动的隔离曲线，如图12（b）所示。从图12（b）可以看出，FSM 闭环控制系统对低频区域扰动的隔离性能基本一致，随着非工作轴固有频率的增加，在非工作轴固有频率处谐振峰值下降。

图12 不同结构固有频率下FSM 闭环控制系统对线加速度扰动隔离曲线Fig.12 Rejection curves for linear acceleration disturbance of FSM closed-loop control system with different structural natural frequencies

同样在FSM 闭环控制下，分析反射镜基座角扰动的隔离性能。以工作轴固有频率为5 Hz、20 Hz、50 Hz，非工作轴固有频率为300 Hz 为例，绘制了其对基座角速率扰动的隔离曲线，如图13（a）所示。从图13（a）可以看出，随着转动固有频率的增加，FSM 闭环控制系统对低频区域扰动的隔离性能提升了，对中频区域扰动隔离性能变差，对高频区域的隔离性能保持不变，在非工作轴固有频率处未出现谐振峰。以工作轴固有频率为20 Hz，非工作轴固有频率为300 Hz、600 Hz、900 Hz 为例，绘制了其对基座角速率扰动的隔离曲线，如图13（b）所示。从图13（b）可知，非工作轴固有频率对基座角速率扰动隔离曲线无影响。

图13 不同结构固有频率下FSM 闭环控制系统对角速率扰动隔离曲线Fig.13 Rejection curves for angular rate disturbance of FSM closed-loop control system with different structural natural frequencies

4 FSM 振动试验

对在研FSM 进行模态测试，测得转动轴固有频率为25 Hz 左右，非工作轴固有频率为515 Hz左右；伺服系统调试后，开环穿越频率为293 Hz，相位裕度设置为52°。开展随机振动试验，随机振动功率谱如图14（a）所示；通过加速度计测量振动台的线加速度，如图14（b）所示。利用FSM 内电涡流传感器测量伺服使能前后FSM 的角位置信号，结果如图15 所示。对角位置信号进行功率谱分析，与振动台功率谱比较，求得FSM 对线振动的隔离度曲线，如图16 所示。从图16 可以看出，在511 Hz 附近存在谐振峰，与非工作轴固有频率接近，与仿真分析结果一致，验证了仿真模型的正确性。另外，实际系统在733 Hz 处结构谐振，可能为反射镜镜体自身的结构特性，在所建立的模型中无法表征。

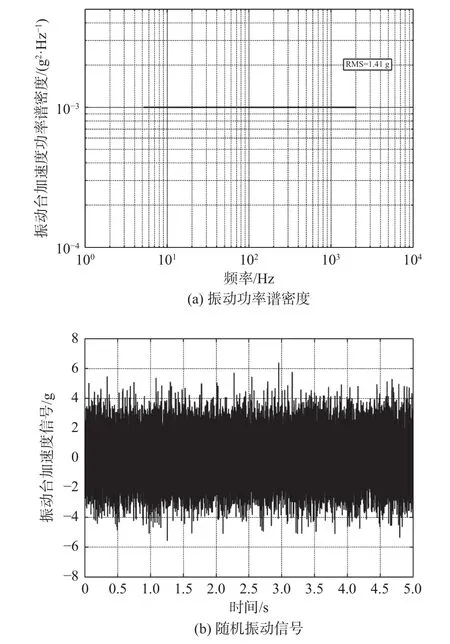
图14 振动台随机振动Fig.14 Random vibration of vibrating table

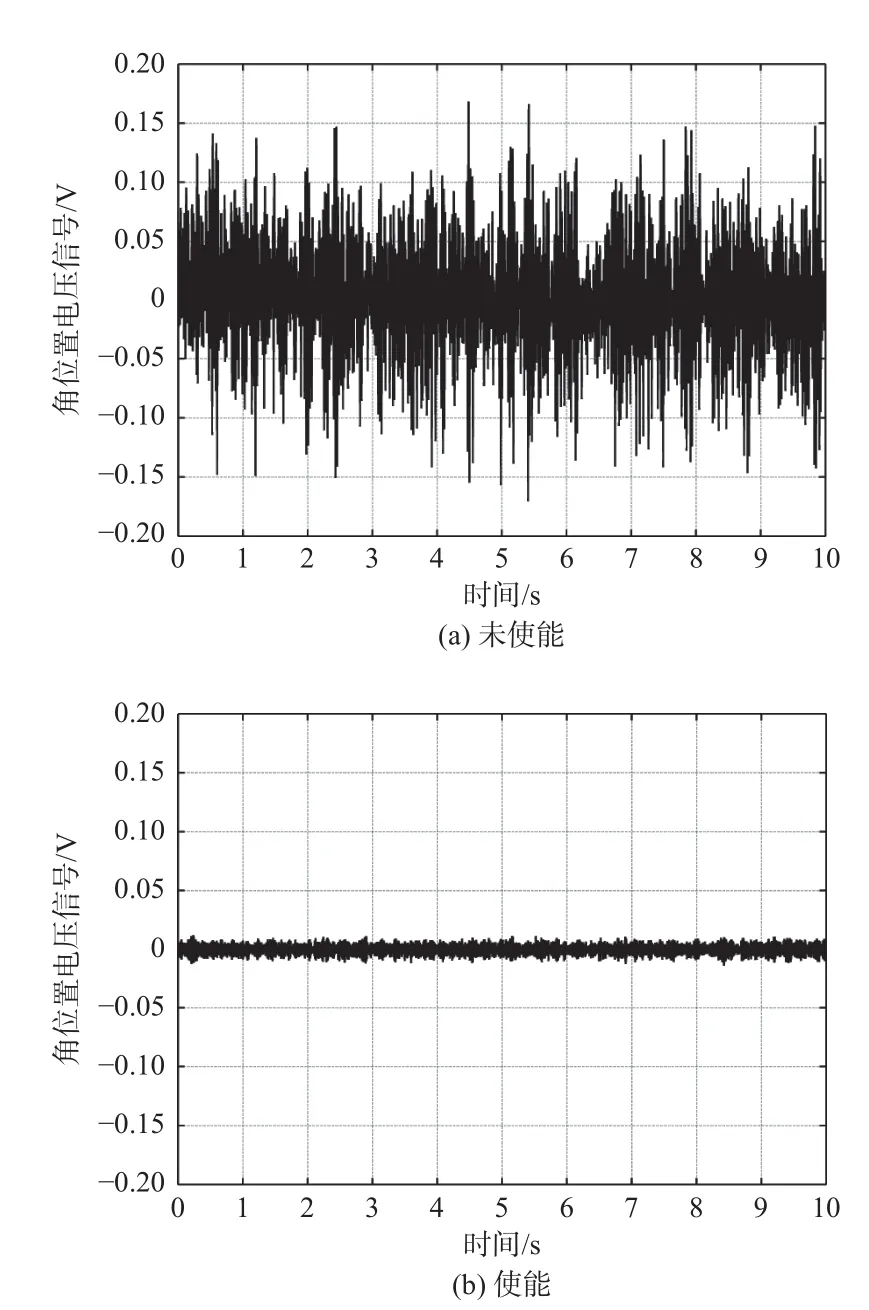
图15 随机振动下FSM 角位置信号Fig.15 Angular position signals of FSM with random vibration

5 结论

通过对FSM 理论建模与仿真分析，并通过振动试验对仿真模型进行了验证，得到以下结论：

1）被控对象特性与电机选型和转动固有频率等有关。在音圈电机选定后，转动固有频率较小时，被控对象为过阻尼系统，其传递函数曲线不会出现谐振峰；转动固有频率较大时，被控对象为欠阻尼系统，其传递函数曲线存在谐振峰，通过速率反馈，可将被控对象调整为临界阻尼系统，从而提升FSM 控制性能。

2）当负载质心偏离柔性铰链转动中心时，反射镜基座的线运动会耦合出角运动，并在平动固有频率处存在谐振峰，而且平动固有频率越高，引起的谐振幅值越小，因此FSM 结构设计时非工作轴固有频率越大越好。

3）对反射镜基座角扰动的隔离性能是：在低频区域转动固有频率增加，对角扰动的隔离性能越好；在中频区域转动固有频率增加，对角扰动的隔离性能变差；在高频区域对角扰动的隔离性能基本保持不变。随着转动固有频率的增大，为了克服柔性铰链弹性力，对音圈电机输出力要求较高，但由于尺寸、重量限制，音圈电机的选择受到限制。在音圈电机选定后，转动固有频率选择过大时，被控对象会出现谐振峰，使得FSM 控制系统复杂或达不到性能要求，因此需要权衡各方面因素，对转动固有频率进行选取。