基于Brown指数平滑模型的自适应R峰探测算法*

郝子浩 张晓明，2

（1.中北大学电子测试技术国家重点实验室 太原 030051）（2.中北大学仪器科学与动态测试教育部重点实验室 太原 030051）

1 引言

心血管疾病已成为全球的头号死因。根据世界卫生组织的研究报告，2019年大约有1790 万人死于心血管疾病，占全球死亡总数的32%。因此在日常生活中及时观测心脏健康状态和及时就医具有重要的意义［1］。目前检测心脏疾病最有效的工具之一是心电图，其中R峰探测是心电图解读中的第一步，只有将R峰确定后才能对其他波形进行分析与提取［2］。

近年来，很多R 波探测算法被提出，大多数R波探测算法分为信号预处理阶段和R 峰探测阶段［3］。信号预处理阶段常用的方法是数字滤波器法［4～5］和小波变化法［6～9］等。数字滤波器法的去噪能力主要取决于滤波器的类型、阶数和截止频率。基于小波变换方法能通过选择高振幅系数来提高信号质量，但是其计算量过大。R 峰探测阶段常用的方法是阈值法［10～12］和神经网络法［13～14］。阈值法的优点在于其计算简单并且可以是自适应的。PT 算法［4］使用了具有自适应性的信号阈值和噪声阈值来探测R峰，在高信噪比心电信号上具有非常好的性能表现。但是在噪声阈值上的设置欠妥，不能充分体现噪声的大小，以至于很难从信号幅值层面找到一个合适的阈值来区分开噪声峰和R 峰。而且PT 算法在阈值更新模型中的参数是固定的，没有充分考虑当前阈值的变化情况和规律，导致更新后的阈值适应性不足。使得PT算法在低信噪比心电信号中性能大幅下降。神经网络法通过对输入和输出间的复杂关系建模以找到心电信号与对应R峰位置之间存在的关系。这种方法需要大量且有效的数据，虽然在数据集上精度高，但是模型可解释性差，且模型复杂。

本文针对可穿戴心电手环中动态强噪声干扰导致的R 峰探测难题，提出了一种基于Brown 指数平滑模型的自适应阈值R峰探测算法。首先，基于R 峰的形态特点和规律选取特征，然后根据所选择特征的变化规律，使用Brown 指数平滑模型更新阈值参数，并通过最小化预测值与观测值的相对误差平方和来得到平滑系数。最后使用回溯判断的方式剔除错检R 峰，填补漏检R 峰，最终实现在强噪声干扰下精准探测R峰的目的。

2 特征选择

2.1 噪声

预处理后的可穿戴心电信号依然存在大量的噪声干扰。由于任务目标是R 峰探测。因此，将R峰以外的信号波形（包含心电信号中的P 波、T 波）全部视为噪声。QRS 复合波持续时间通常在0.1s左右，因此将噪声区域设定为R 峰前后0.1s内的区域，在此区域中的ECG 信号都被视为噪声。噪声区域中数据的最大值就为噪声的观测值，如图1表示。

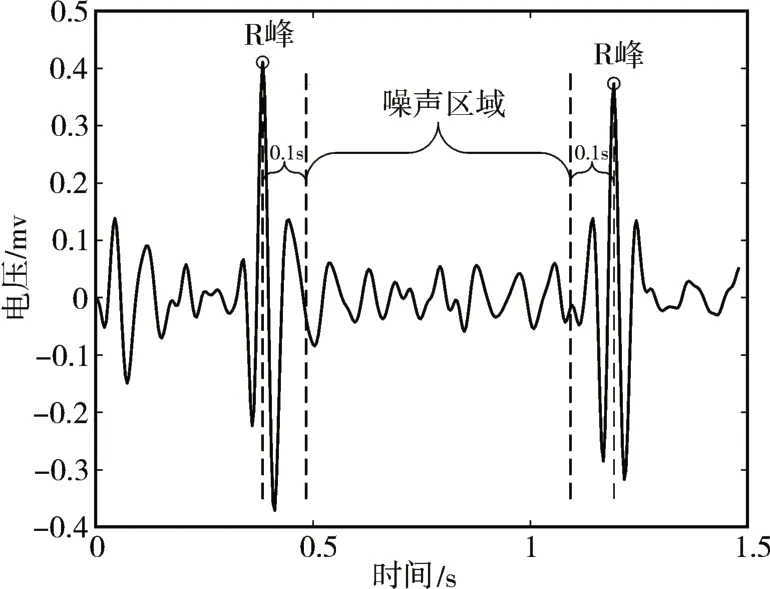
图1 设定噪声区域和当前噪声大小

2.2 R峰阈值

为了能够在信号幅值层面区分开噪声峰和R峰，R 峰阈值应位于最大噪声峰幅值和R 峰幅值之间，如图2所示。

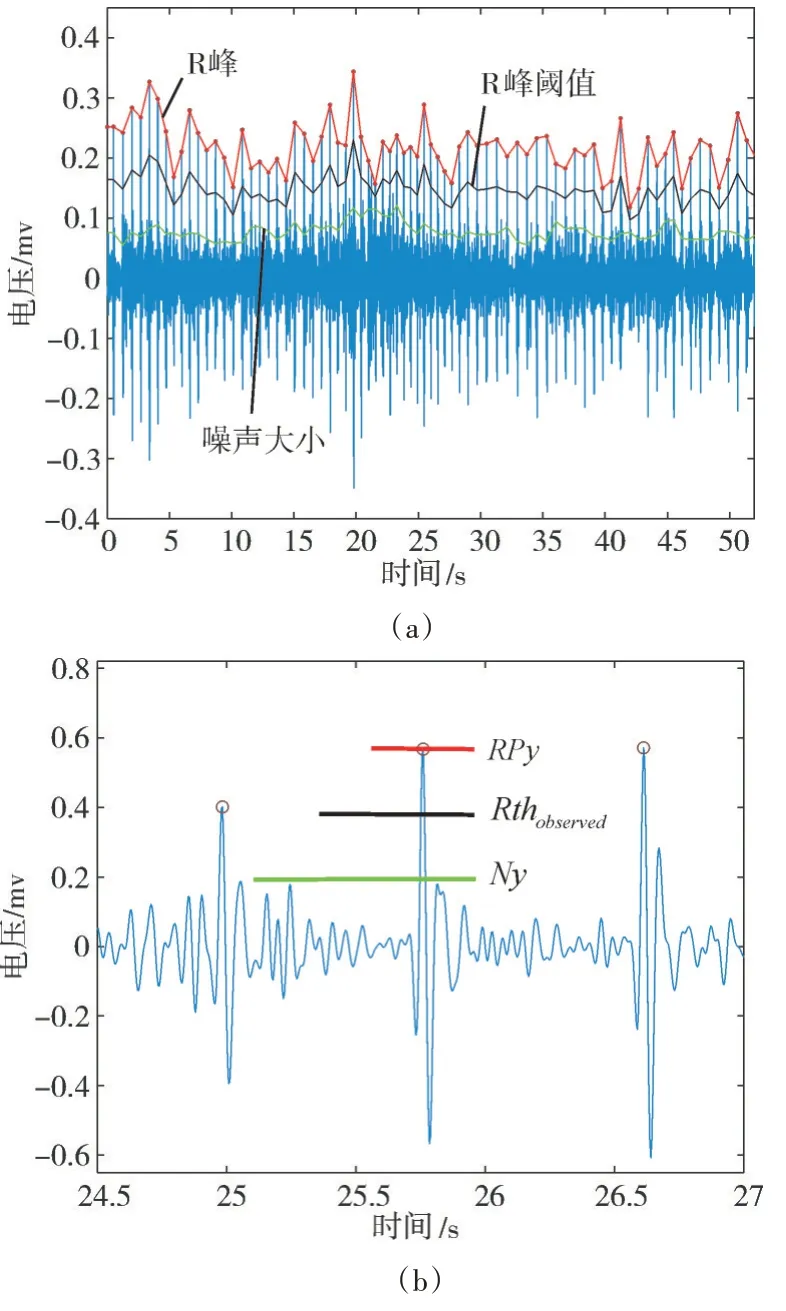
图2 （a）噪声干扰下的R峰曲线、噪声峰曲线和合适的R峰阈值曲线（b）R峰阈值的观测值在心电信号中的位置

图3 实验室自研的可穿戴心电手环

每探测一个R 峰后，可以根据此R 峰的幅值和前一刻观测到的噪声大小反推出适合探测此R 峰的R 峰阈值，将此R 峰阈值定义为R 峰阈值的观测值，其公式如下：

Rthobserved=Nyobserved+K(RPy-Nyobserved)

其中Nyobserved表示噪声的观测值，RPy表示R峰幅值，Rthobserved表示R 峰阈值的观测值，K表示R 峰幅值与噪声的观测值之间的间隔系数，为了平衡两者的影响，取0.5。

2.3 RR间隔

RR间隔表示人体的心脏搏动周期。人在静息状态下，RR间隔处于一个稳定波动的状态，即使在剧烈运动后，RR 间隔也呈现缓慢变化。根据心电信号的这个特点，可以从时间层面对所探测R峰进行异常诊断，从而辅助R峰的探测。

3 Brown指数平滑模型

Brown 指数平滑模型是一种短期预测方法，具有对观测量变化的快速反应速度和对观测误差的修匀能力［15］，因此本文使用Brown 指数平滑模型方法对阈值和参数进行更新。

设{Yi|i=0，1，2，…，k} 为观测值序列，{Si|i=1，2，…，k}为预测值序列。其计算公式如下：

在Brown 指数平滑模型中，平滑系数α表示了未来预测值对过去数据和当前数据的依赖程度。随着观测信息的久远，其对应的权重呈现指数级降低。因此，Brown 指数平滑法是从时间层面确定观测信息权重的，越临近当前的观测值，赋予更高的权重，反之赋予的权重越小。在实际预测过程中，平滑系数α具有调整模型对观测误差的修匀能力和对观测量变化的反应速度的作用。凭经验预测时，如果历史数据比较平稳，平滑系数α往往取小些，以提高对观测误差的修正能力；如果历史数据变化较大，平滑系数α则取大些，以提高对观测量变化的反应速度。

由于平滑系数α决定了对观测误差的修匀能力和对观测量变化的反应速度，所以带来了既要提高平滑系数α值以增加对观测量变化的反应速度，又要降低平滑系数α值以增加对观测误差的修匀能力的矛盾，因此平滑系数α的选择需要慎重考虑。

考虑到使用绝对误差最小二乘法拟合平滑系数α时，忽略了观测量本身的大小，因此本文使用相对误差最小二乘法来对平滑系数α进行自动调整。通过最小化预测值与观测值的相对误差平方和来得到最优的平滑系数α。

在使用相对误差最小二乘法时，需要历史数据进行拟合，因此，早期的平滑系数α依据预测对象的特性凭借经验而确定。

R 峰阈值的大小受噪声和R 峰幅值影响，虽然噪声变化较大，但是R 峰幅值是较为稳定的，且在R 峰阈值的计算公式中平衡了噪声和R 峰幅值的影响，因此其平稳性较高，所以设置较小的早期平滑系数α，αR=0.4。

噪声处于动态变化当中，其平稳性较弱，为了能够提高对噪声变化的反应速度，因此设置较大的早期平滑系数α，αR=0.8。

RR 间隔代表心脏跳动的间隔时间，其变化是较为缓慢的，即使在剧烈运动后心率也呈现缓慢的下降，因此，设置较小的平滑系数α，αR=0.3。

4 基于Brown 指数平滑方法的自适应R峰探测算法

4.1 预处理

预处理阶段的目的是提高信噪比。此阶段使用了分帧和带通滤波。心电图机可测量的最大心跳周期时间为2s，为了保证每帧信号中最少存在1个QRS 复合波，因此设置3s 为一个时间周期。ECG 信号中QRS 波的频谱范围主要在10Hz～25Hz，因此本文采用了8 阶截止频率为10Hz 和25Hz 的巴特沃斯带通滤波器来滤除噪声，消除噪声对于R峰探测的干扰。

4.2 峰值探测

4.2.1 基于R峰阈值的峰值探测

在这一阶段，首先对此帧ECG信号进行基于R峰阈值的峰值探测，R 峰间隔阈值设置为0.2s。然后按时间顺序将探测到的局部峰值与R 峰阈值比较大小，大于R 峰阈值的局部峰值点，我们将它视为R波点。

4.2.2 异常状态回溯判断

RR 间隔变化缓慢，利用这个特点来填补漏检R峰和消除错检R峰。

1）基于Brown指数平滑模型的RR间隔预测。

2）RR 间隔异常回溯判断。当目前所探测RR间隔与预测RR 间隔值的差值过大时，判定当前探测R峰可能存在异常。继而比较当前RR间隔与预测RR 间隔值的大小，当当前RR 间隔较大时，表明RR 间隔异常原因可能是R 峰漏检导致，当预测RR间隔值较大时，表明RR 间隔异常原因可能是R 峰错检导致。然后跟踪记录前后各4 个RR 间隔的大小，目的是依据RR 间隔的平稳性利用更多的前后关联信息来判定R峰异常情况，之后的步骤如下。

对于可能是R 峰漏检导致的RR 间隔异常情况，如果前三个RRI平均值和后三个RRI平均值的差值小于0.15s，判定RR 间隔异常原因确实为R 峰漏检导致，之后进行漏检填补操作，否则即为心脏异常跳动情况，而非R峰探测错误。

对于可能是R 峰错检导致的RR 间隔异常情况，如果前三个RRI平均值和后三个RRI平均值的差值小于0.15s，判定RR 间隔异常原因确实为R 峰错检导致，之后进行R 峰错检消除操作，否则即为心脏异常跳动情况，而非R峰探测错误。

4.2.3 漏检R峰填补

在判定RR 间隔异常原因为R 峰漏检导致后，开始漏检R 峰填补操作。操作具体为寻找前一个R 峰与当前R 峰之间大于所预测噪声幅值的局部峰值点，并选取其中幅值最大的峰值点作为漏检的R峰，其他情况不考虑。

4.2.4 错检R峰消除

在判定RR 间隔异常原因为R 峰错检导致后，开始错检R 峰消除操作。首先，计算异常RR 间隔的前一个RR 间隔和后一个RR 间隔与其他6个RR间隔平均值的差值。然后，比较这两个差值的大小。如果前一个差值大，则表示错检R峰是计算异常RR 间隔的起始R 峰，否则错检R 峰是计算异常RR 间隔的末尾R 峰。最后，将定位到的错检R 峰予以消除。

5 实验结果与讨论

5.1 信号数据库

本文使用的是自建的可穿戴单导联心电信号数据集。数据集中包含了80 条长达5min 的ECG信号。该数据集的采样率为250Hz，实验者年龄从19 到25 岁，男性5 人，女性5 人。分别记录了每个人在不同时间段不同环境下的心电信号。

5.2 性能评估

将本文提出的算法与Pan 等提出的R 波探测算法（PT 算法）应用于自建的数据集，通过精度、召回率和F1 分数来评价算法的性能，具体如表1所示。

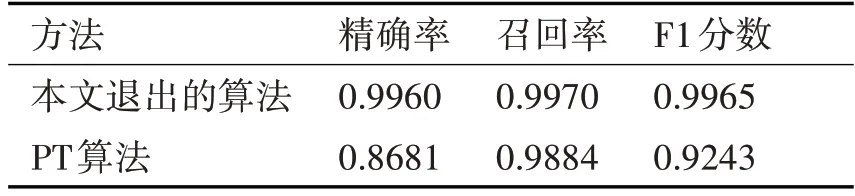
表1 提出的自适应阈值R峰探测算法与Pan等提出的算法的性能比较

本文提出的算法获得了更高的检测精度，而PT 算法表现较差的原因首先在于噪声的观测不准确，导致R 峰探测阈值不能准确区分噪声峰和R峰，第二是没有充分利用RR间隔的特性，很多错检R 峰处在真实R 峰之间，间隔较近，严重不符合正常的RR间隔范围。

5.3 不同信噪比下算法的表现

为了验证所提出算法在强噪声下的抗干扰能力，进行噪声仿真实验。向原始心电信号加入不同信噪比的高斯白噪声，然后使用本文提出的R峰探测算法和PT算法对R峰进行探测。

从图5中可以看出，在相同信噪比下，本文提出的方法获得了更高的F1 分数。并且随着信噪比的增加，相比PT 算法法本文所提出方法的F1 分数下降较为缓慢。这表示了在一定噪声干扰下，所提出的算法依然可以实现高准确率的R峰探测，体现了所提出算法对于噪声的鲁棒性。

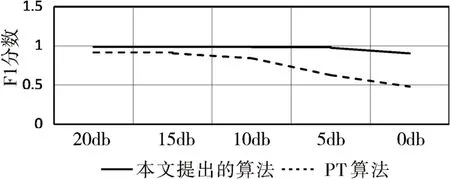
图5 不同信噪比下R峰探测结果

6 结语

本文针对可穿戴心电手环中动态强噪声干扰导致的R 峰探测难题，提出了一种基于Brown 指数平滑模型的自适应R 峰探测算法。首先，基于R 峰在可穿戴单导联心电信号中的形态特点和规律选取特征。然后根据所选择特征的变化规律，使用Brown 指数平滑模型更新阈值。最后通过回溯判断方法剔除错检R 峰，填补漏检R 峰。本文在自建数据集上对算法进行了性能评估，所提出算法在精度、召回率和F1 分数上分别达到了99.6%、99.7%和99.65%，并与PT算法进行了比较，证明了所提出算法在强噪声干扰下的鲁棒性。