基于声阵列炸点定位系统的时延判定算法研究*
王 琦 李 明 英俊杰
(西安工业大学电子与信息工程学院 西安 710021)
1 引言
炸点位置测试是常规靶场中重要的测试项目之一。利用爆炸时产生的声信号正确估计出炸点的空间位置坐标,是炸点坐标测试技术中的关键环节。被动声传感器阵列定位技术成本低、隐蔽性强且可全天候探测,根据特定的几何结构布置声传感器,采用时间差方法进行定位,即可探测到弹丸爆炸的位置信息[1]。爆炸声通过声波传播时,近地炸点的爆炸物在膨胀过程中易受地面阻挡或山体、建筑遮挡,会形成混响,从而造成炸点信号识别困难[2]。声传感阵列定位技术中一般采用无线传感器网络,将具有无线通信功能的传感器模块搭载在声传感器上作为一个传感器节点,通过信号处理方法对采集到的声源信号进行处理,结合声传感器阵列的几何结构得到目标的位置信息。并行分布式声传感器阵列利用各个声传感器所测声源的目标信号,经过信号处理的方法计算出声源的坐标[3~5],仅在每个节点采用一个声传感器,因此分布式声传感阵列的计算复杂度要求不高,利于达到定位系统的实时实现。其中王洋等[6]提出基于时间差技术的五元十字阵算法,而本文选用的立体五元声阵列较平面阵能给出更准确声源三维位置。严天峰[7]结合接收信号自相关和互相关函数的特性,提出了基于二次相关的时延估计方法,减少了噪声对互相关函数的影响。这些文献所研究的方法对测量弹丸炸点参数具有推动作用,为了进一步提升弹丸落炸点参数精度,本文提出一种基于时延判定法的分布式声传感阵列炸点位置融合算法,研究一种存在混响时的炸点位置测试方法。
2 五元声阵列探测模型的建立
本文构建的多声传感阵列弹丸炸点位置测试系统主要由五个相同的声传感器组成,其中五个声传感器呈正四棱锥分布。测试系统的工作原理为当弹丸在指定的探测区域爆炸时,会触发声传感器采集炸点爆炸的声信号。同时,根据五元声阵列的空间布置关系,结合每个声传感器输出炸点位置的时刻值,解算出弹丸炸点位置坐标为P(x,y,z)。如图1所示五个声传感器呈正四棱锥分布,声传感器N0位于正四棱锥顶点处,其余四个声传感器分别分布在底面四个顶点,声传感器N1,N2,N3和N4沿逆时针方向分别放置,各个顶点到坐标系原点的距离记为D,声传感器N0的高度记为H。其中,N0,N1,N2,N3,N4为五个声传感器,则N0,N1,N2,N3,N4的坐标分别为(0,0,H),(D,0,0),(0,D,0),(-D,0,0),(0,-D,0)。
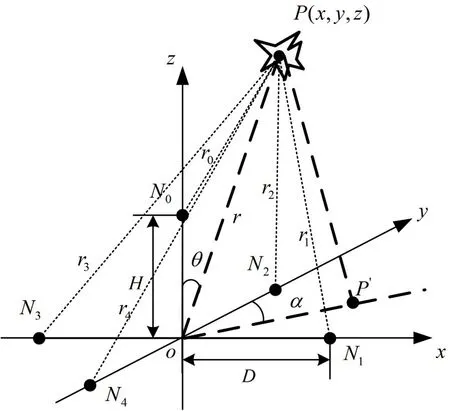
图1 五元声阵列炸点位置测试示意图
为了方便计算弹丸炸点位置,假设在坐标系oxyz中的炸点位置为点P(x,y,z),炸点P与每个声传感器的距离分别为r0~r4,每个声传感器N0、N1、N2、N3、N4捕获的弹丸爆炸声时刻分别记为t0、t1、t2、t3、t4,则爆炸声信号到达N0与到达N1的相对时延为T0i=ti-t0,其中i=1,2,3,4,可获得弹丸炸点位置与五个声传感器的时空函数,即:
式中,c为当前声速。
同时,根据图1可知,在坐标系oxyz中,炸点P相对于坐标原点O 的方位角为α,俯仰角为θ,弹丸炸点坐标P(x,y,z)的球面坐标系可表示为
结合式(1)和式(2),可以得到,方位角、俯仰角和探测距离的表达式为
将式(3)、(4)、(5)带入式(2),可以解算出炸点P在坐标系oxyz中的位置信息。由式(3)~(5)可以看出,影响坐标测试的关键因素是时延值的获取,所以能够准确识别弹丸炸点的时刻值获取到精确的时延值对系统的测试精度十分重要。
3 时延判定算法
对于任意两路声信号的时延差值可以采用广义互相关法(Generialized Cross-Correlation)来估计一个信号达到两个传感器的时间延迟。假设两个声传感器接收到的信号可以分别表示为x1(t)和x2(t),两路信号的广义互相关函数Rx1x2(τ)等于互功率谱的傅里叶变换[8~10],如下式表示:
其中,Gx1x2(ω)=x1(ω)x2*(ω)表示被测信号x1(t)、x2(t)的互功率谱密度函数;x1(ω)、x2(ω)分别表示声传感器N1,N2接收到信号x1(t)、x2(t)的傅里叶变换,*表示复共轭。
但在复杂背景的环境下,各类噪声下的干扰容易引起互相关函数峰值变宽,出现假峰值。为了抑制噪声的干扰,选择在信号中加入加权函数,提高互相关函数的抗噪声能力。在实际应用中,选择合适的加权函数对GCC 函数的性能非常重要,本文经过对比之后选择PHAT加权函数:
将PHAT 加权函数带入式(6),两信号的广义互相关函数如下:
在高信噪比(SNR)的情况下,Rx1x2(τ)会得到明显的峰值,但是存在混响以及噪声信号与目标信号相似时[11~12],PHAT 加权广义互相关函数也会出现多个峰值的情况。除了在真实时延处出现一个峰值外,还会受到相似信号的影响在其他位置出现另外的峰值,其相关程度与相似信号的幅度大小有关。针对以上情况,同时考虑到声源定位中无线传感器网络的特点,本文提出了一种时延判定算法,探讨了在有混响的情况下,采用时延判决的方法对已经得到的时延值进行二次处理,该方法通过最小均方误差准则在一组可能的TDOA 估计值中检测出真实值,从而计算目标的声源位置。
将五元立体声阵列中声传感器N0为中心节点,其余四个声传感器节点以半径为R的距离分布在中心节点四周。因为声传感器阵列有着特定的几何结构,故任意两个声传感器之间的真实时延差值与目标同传感器节点之间的距离存在着严格的对应关系,而由混响产生的时延差值则不具有这样的特性,即相关函数中虚假峰值,所以本文提出的时延判定算法如下。
根据经验得出的信噪比选定阈值H,分别搜索相关函数R01(τ)、R02(τ)、R03(τ)、R04(τ)大于这一阈值时所对应时延的值。假设通过广义互相关法每两个传感器得到的时延分别都存在n 个时延量,说明有虚假信号的出现。其R0i(τ)得到的时延分别为{ΔTi1,ΔTi2,…,ΔTin},其中i=1,2,3,4。在四个集合中分别选取一个元素进行组合一共可以得到组时延向量,分别记为
其中,将A1,A2,…,Am称为原时延向量组。
分别将以上的m组时延向量根据五元立体声阵列炸点位置定位计算方法建立方程组求解目标位置,得到m个目标位置向量P1,P2,…,Pm。
用得到的目标位置向量计算时延向量为
其中,v为声速,将τ1,τ2,…,τm称为新时延向量,计算均方误差:
其中使RMSE达到最小值时的m对应的Pm作为炸点目标的位置(x,y,z)。
本文提出的时延判定算法的流程图如图2所示,其基本思想就是只有真实的时延与目标同声传感器节点之间的距离存在严格的对应关系,而由混响和外界环境产生的相似信号得到的时延则不具有这样的特性,所以当由虚假的时延得到的定位结果反演时延前后的均方误差较大。而由真实时延得到的定位结果反演时延前后的均方误差较小。当新时延向量均方误差达到最小时的原时延向量即为真实的时延向量。因为在实际测试中,每个声传感器得到的原始声信号进行相关函数运算中由于混响产生的尖峰数目不会很多,所以A1,A2,…,Am的值不会很大,整个过程的计算量也不会很大,所以具有实用价值。
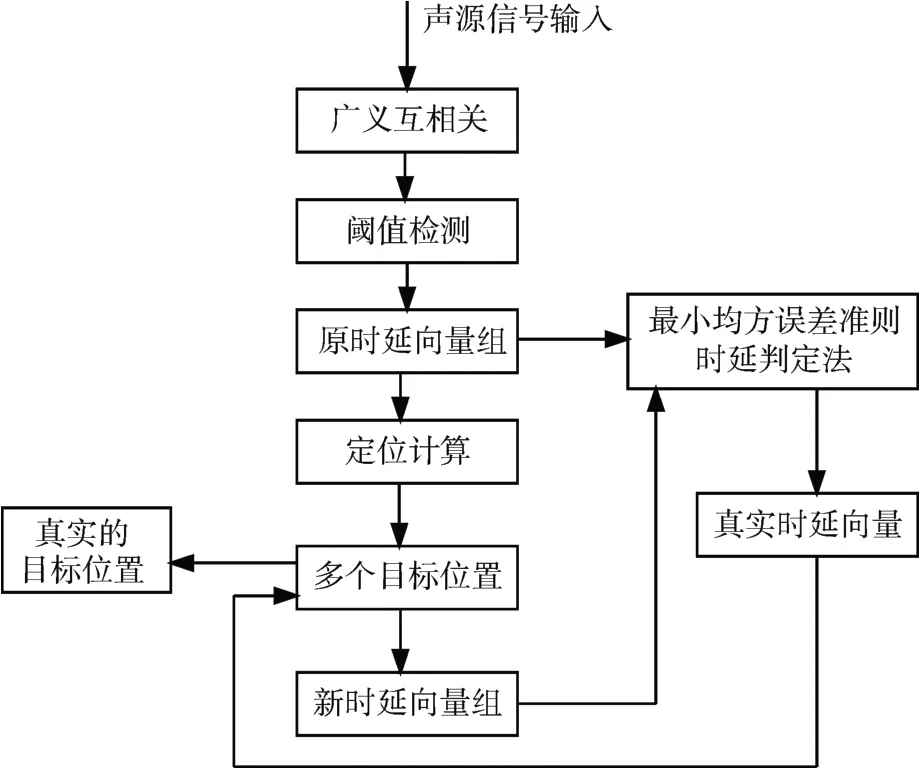
图2 时延判定法流程图
4 实验与分析
为了评估基于时延判决准则的并行分布式融合算法在真实环境中的可行性,在空旷的室外进行测试,选择无风的天气进行实验,测试出当时的声速为c=341m/s。采用5个高精度声传感器按照第2 节建立的声阵列炸点位置探测模型进行布置,其中,5个声传感器节点N0,N1,N2,N3,N4的坐标分别为(0,0,2),(2,0,0),(0,2,0),(-2,0,0),(0,-2,0),单位为m。每个声传感器都设有独立的采集装置,采集装置带有同步触发信号输入端口和无线传输模块。当弹丸爆炸后,声传感器开始采集声信号,再由无线通信模块传送到终端处理计算机,终端处理计算机根据接收到的多路声传感器信号,经信号滤波处理和互相关函数法,提取各个声传感器输出弹丸炸点声信号的时延信息。
通过选取采集的语音信号,对其分别进行互相关算法和广义互相关算法求取其时延值。五个声传感器对某一发爆炸声音采集到的声信号进行处理,采集到的炸点原始声信号波形信号如图3所示。
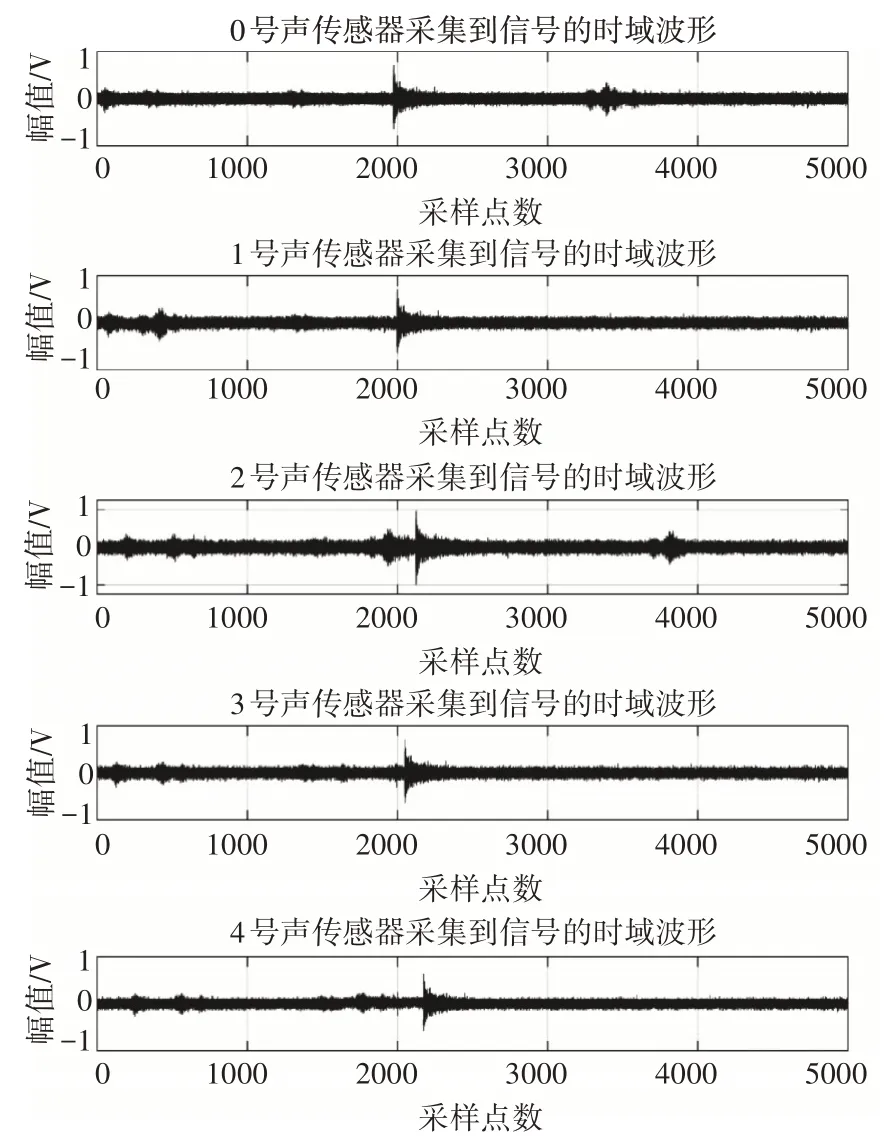
图3 爆炸声原始信号
当测试现场空旷无混响时,普通互相关法和广义加权互相关法都可以得到准确的时延值,选取N0和N1声传感器进行互相关求解,得到的时延值为3.5ms,如图4所示。由图4也可看出,在现场环境中存在未知噪声时,PHAT 加权的广义互相关法比普通互相关法能更加明显地获取到波形峰值。
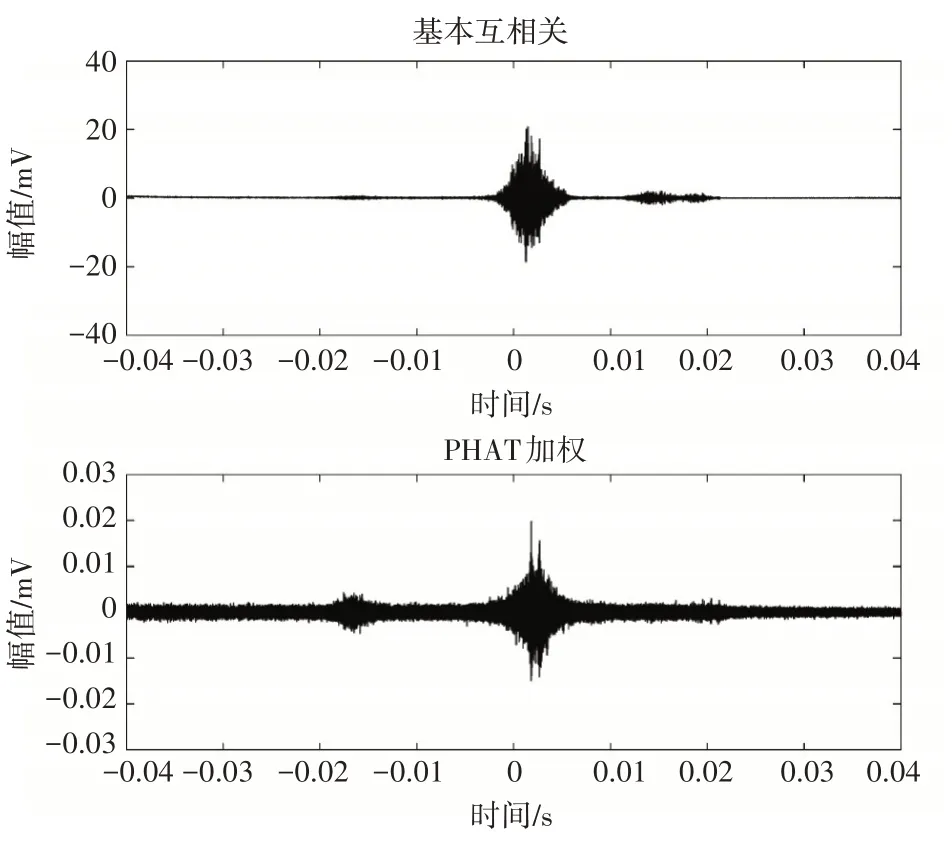
图4 无混响时互相关结果
本文通过将某一路信号时延后模拟混响信号,得到带混响的信号后,再次采用两种相关函数法进行仿真,如图5所示。从图5中可以看出,普通互相关法和PHAT 加权法都得到了若干个峰值,此时无法分辨真正的时延。若再次用峰值检测法获取时延时会得到错误时延值,所以我们选择获取阈值H以上的时延值,采用时延判定法进行处理。
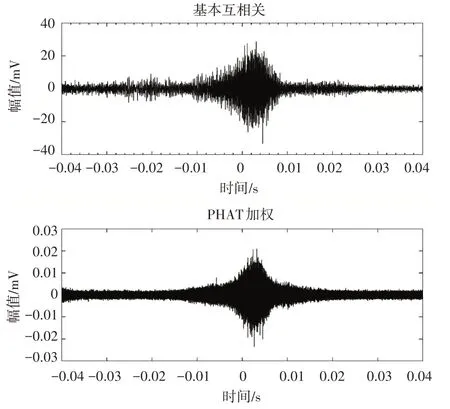
图5 存在混响时的互相关结果
从上面的实验结果中可以看出:在真实的测试环境中,由于环境因素的复杂,PHAT 加权的广义互相关法比普通互相关法获取的波形峰值更加明显,更适合于获取到准确的时延;而在存在混响及相似信号的影响下,PHAT 加权的广义互相关法仍然比普通互相关法获取的虚假峰值少,表明其滤除噪声的性能更强,但其仍旧不能准确地获取到时延信息,由此采用本文提出的时延判定法进行二次处理。
通过选取不同测量值时RMSE较小时的值,将该时延值作为分布式声源定位的准确时延值。为了进一步验证分布式时延判定法的可行性,本文对这发弹丸进行误差计算。根据现场测定,爆炸声位于P(8,7,2)处,依据本文提出的五元立体声阵列炸点位置测试方法可知节点N0与节点N1,N2,N3和N4的真实时延向量为(3.5,2.9,-5.1,-4.6),单位是ms,声速c=338.9m/s。时延判定法的阈值为H=0.017,得到以下时延向量组:
R01(τ)={ΔT11,ΔT12}={3.5,3.2},
R02(τ)={ΔT21,ΔT22}={2.9,2.5},
R03(τ)={ΔT31}={-5.1},
R04(τ)={ΔT41}={-4.6}。
分别将其排列组合成四组时延向量,即A1,A2,A3,A4,将其代入式(2)进行声源定位,得到目标位置P1,P2,P3,P4。再利用得到的目标位置以及声传感器的位置代入式(1)重新计算时延得到新时延向量组τ1,τ2,τ3,τ4。原时延向量和新时延向量的均方误差统计见表1。
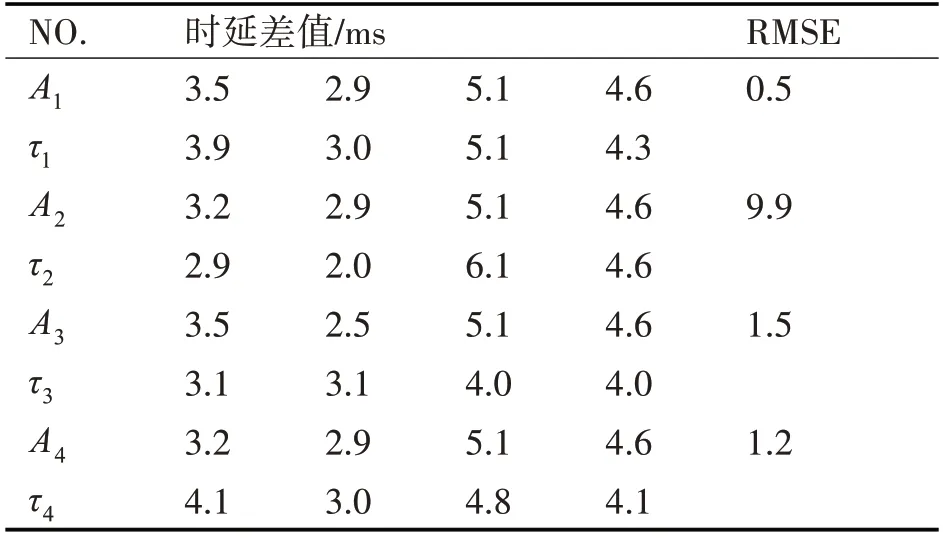
表1 前后时延的均方误差统计
根据表1可以看出,第一组原时延向量与新时延向量的均方误差与其他组相比最小,仅为0.5,同时第一组就是真实时延向量组,而其它含有混响得到的时延向量组的前后时延的均方误差均比真实时延向量组的大。仿真数据验证了本文中提出的时延判定法的可行性与有效性。同时验证了真实时延与目标同传感器节点之间的距离有着严格的对应关系,而由混响产生的时延则不具有这样的特性。所以当由虚假的时延得到的定位结果反算时延时前后时延误差较大。而由真实时延得到的定位结果反算时延时前后时延误差较小。以上分析说明,本文中提出的基于时延判定法的分布式声传感融合算法是可靠有效的。
5 结语
在声阵列炸点位置测试方法中,互相关法由于其简单实用具有广泛的应用价值,但在存在混响或者相似信号的情况下,将很难获取到准确的时延值,甚至会给出错误值导致炸点定位误差极大。考虑到基于声传感器的无线传感网络这一领域,本论文以五元立体声阵列为炸点测试基阵,运用广义互相关法进行多弹丸爆炸声信号的时延估计,采用时延判定法能够在一组多个时延向量中判决出真实的时延向量,根据得到的真实时延向量计算出目标的真实位置。由于靶场的试验环境存在多种随机干扰因素,对强烈的外界干扰及相似信号的干扰本测试方法提出新的时延判定法为后续的炸点位置估计提供了很好的解决方案。

