基于三维走时的冲击波超压场重建方法*

刘晓佳 李 剑 孙泽鹏 马明星 魏晓曼

（中北大学信息探测与处理山西省重点实验室 太原 030051）

1 引言

爆炸原理是物体在某极短的时间范围内，释放射出来大量热能量，产生高温，同时破坏性极强，难以通过直接观察的方式研究。随着战斗部研制向着智能化，一体化发展，对于爆炸场的压力毁伤能力等参量研究具有重要意义。但是由于传感器节点布设难度大等问题，有限的数据无法直接、全面地判断弹药的毁伤能力，因此冲击波场重建对于弹药研发过程和定性验证是至关重要的。

目前，冲击波超压场重建的方法有层析成像法，插值重建法等，白苗苗等［1］针对爆炸过程中获得的数据较少，对反演速度和精度进行分析，加入先验值进行EM 反演；郭亚丽等［2］针对冲击波峰值超压经验公式的求解的局限性，利用广义逆方法进行系数矩阵求解，对网格单元加重权，对冲击波速度场参数进行反演，再进而根据冲击波峰值的超压系数与冲击波速度分布的函数关系可得到超压分布，其重建的结果远远优于经验公式；杨志等［3］采对冲击波压力场进行插值，对比多种方法，表明B样条插值算法效果最好；赵化彬等［4］提出了一种基于非均匀的有理B 样条（NURBS）“蛛网”插值的场重建方法；张晓光［5］将多元多项式理论应用到冲击波峰值插值理论计算中，拟合出波后衰减波形进行弹药冲击波重建；姚悦［6］利用Biharmonic 样条曲面插值算法进行超压峰值重建；郭晶［7］提出了一种利用摄像机对冲击波场进行拍照记录得到冲击波波阵面的传播速度对当量进行估算，分析爆炸过程。目前科研人员集中研究二维冲击波场重建方法。由于爆炸冲击波是各向异性，常规的二维传播模型无法有效表征三维空间的传播特性。因此，三维冲击波超压场重建是大威力弹药毁伤威力评估时亟待解决的瓶颈问题。

针对上述问题，本文在二维走时层析成像模型的基础上，结合射线追踪理论，建立了三维冲击波超压场重建模型，由于三维超压场重建问题是大型稀疏矩阵求解问题，且传统重建算法对边缘噪声的抑制效果较差，在层析成像的基础上结合了压缩感知理论中的字典学习（Dictionary Learning）联合全变分（Total Variation）正则化，提出了TV-DL 迭代修正算法，为三维冲击波超压场重建及实现其全方位可视化提供了一种新方法，提高了冲击波超压场的重建精度。

2 三维冲击波超压场重建原理

炸药在空气中快速爆炸，瞬时所产生爆炸的爆炸高压一般可达1010Pa，空气爆炸的瞬时初始压力大约为105Pa，爆炸产物极速膨胀，对空气进行压缩，形成爆炸冲击波，由于冲击波传播速度较快（瞬时10-6s）可以认为是沿直射线方向传播的，走时可以通过速度和路径长度之间的函数来表示，如下式：

其中，t为冲击波到达探测点的时间，即为走时；L为冲击波到达测点的传播路径；v 为冲击波波速；S 为慢度；r为对应射线。

假设将重建范围划分为M×N×K=J个网格，对式（1）进行离散化处理，如图1所示。

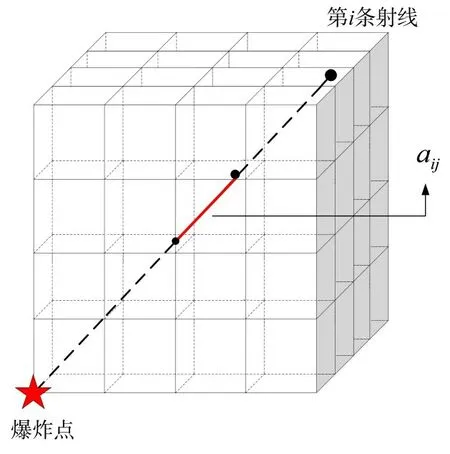
图1 三维离散化示意图

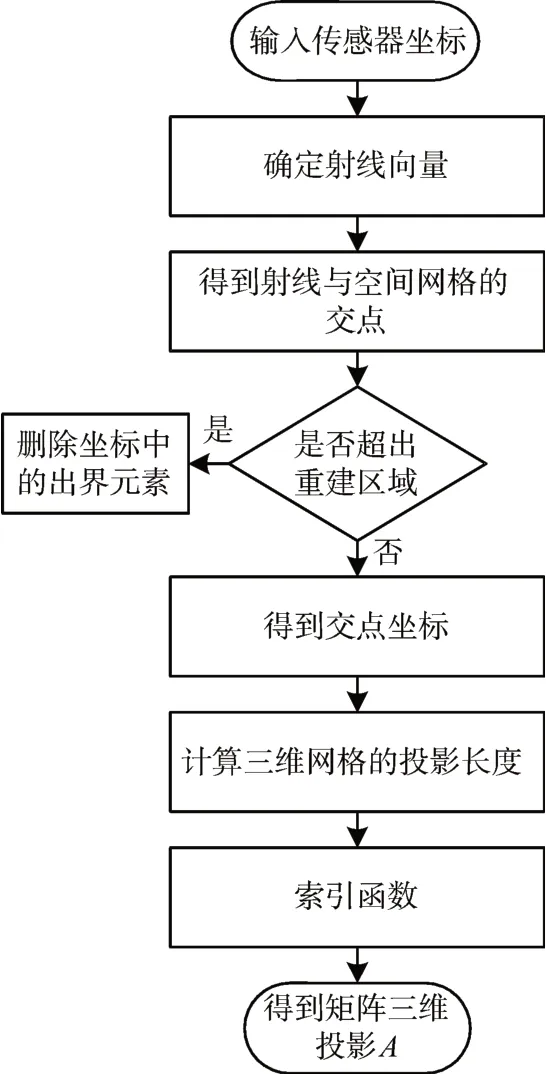
图2 求解三维投影矩阵流程图

上图为三维空间中第i 条射线路径上射线穿过各网格的投影值之和，其函数表达式如下式：

其中，I 为射线总数，即测点个数；J 为离散网格总数；ti为第i 条射线的走时，即信号到达第i 个探测点前的时间；aij为第i 条投影射线穿过第j 个投影网格的投影射线长度，即系数投影矩阵。

上式可总结为矩阵形式：

其中，A 为投影矩阵向量，其大小为I×(M×N×K)的二维矩阵，S 为慢度向量矩阵，其大小为(M×N×K)×1 的一维矩阵，T 为走时向量矩阵，其大小为I×1的一维矩阵。

在建立三维冲击波超压场模型的基础上，矩阵A 的求解是构建三维模型的关键，投影矩阵A 实际上就是I 条射线在三维空间中所有网格的长度信息，本文基于射线追踪最短路径的原理计算矩阵A，具体实现流程如下。

在求射线与网格交点的时候，本文采用先得到射线与网格交点一轴的坐标点，根据比例关系求得其他两轴坐标点，计算步骤如式（4）。

其中，steplen 为步长，lx为区域长度，Bx为传感器x坐标，By、Bz同理为传感器的y、z坐标。

本文投影矩阵A 为二维矩阵，索引函数就是将求得的离散网格内的数据还原到对应三维空间位置处。

3 三维重建模型迭代修正算法

三维冲击波超压场重建过程中，重建区域大，但是爆炸过程破坏性极大，导致可布设的测点少，三维重建问题是一个典型的病态稀疏矩阵的求解问题。传统的迭代重建算法重建误差较大，针对这个问题，利用压缩感知在稀疏矩阵约束方面的优势［10～12］，本文在建立三维冲击波超压场模型（3）基础上，利用字典学习对图像的稀疏表征优势［14～15］，全变分（Total Variation，TV）最小化将重建问题转变为求解最小值的问题，TV 最小化理论对图像边缘纹理的保真特性［13］，实现对层析模型的正则约束。将TV 最小化与字典学习相结合，重新构建了重建模型：

其中A为投影矩阵，S为重建矩阵，T为投影数据。第一项为重建数据的保真项，第二项为正则项，第三项为字典学习项。μ为保真项系数，λ和β为正则项系数。

求解目标函数（5）步骤如下：

步骤一：固定D和αj，更新重建矩阵S，目标函数为

为求解式（6），引入辅助变量dx，dy，bx，by，得到目标函数（9）：

步骤二：固定S，更新D和αj，对应的目标函数如下：

首先进行字典更新，固定αj更新D，使用K-SVD 方法从重建数据S中学习字典。然后进行稀疏表示，固定D更新αj，采用OMP 方法来更新稀疏表示系数αj。

4 实验仿真与结果分析

为验证本文的三维冲击波超压场重建模型的可行性，采用ART 算法、SART 算法和TV-DL 方法进行三维仿真重建实验，比较上述三种算法各自的重建仿真效果以及实现冲击波三维重建的可视化。

设置大小为24m×24m×12m 的矩形区域为重建区域，区域被均匀地划分为1m×1m×1m 的网格，重建模型中添加了7.5%的随机噪声，炸点位置坐标为（0，0，0），仿真以整个重建区域的四分之一为例，待重建区域大小为12m×12m×12m，被划分为1728 个网格，布设了36 个传感器（即36 个测点），图3为传感器布设，图4为各射线与三维网格的交点图。在图4中，共有36 条不同颜色的点线，每个颜色的点线代表着一条射线（即爆炸点到一个测点的传播路径）与途经网格的交点。

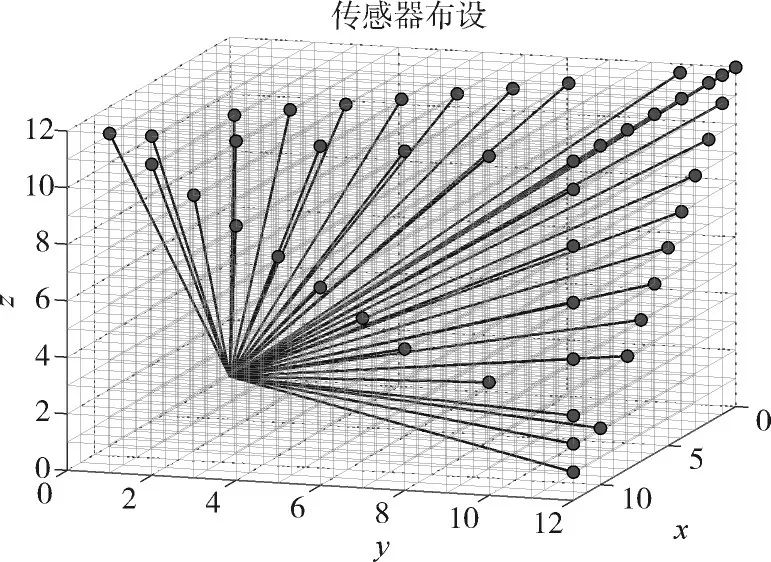
图3 传感器分布图

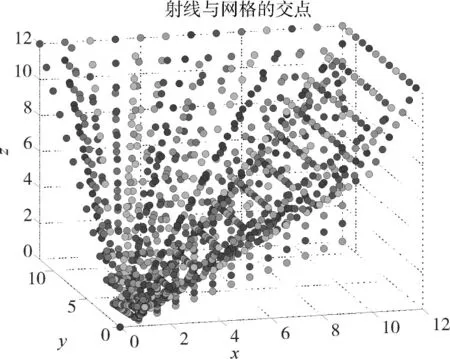
图4 射线与网格交点

仿真实验的TNT 当量为5kg，重建模型选用Henrych 冲击波超压经验公式，根据冲击波峰值超压与速度的关系将模型转化为冲击波波速，将对冲击波超压场重建问题转化为对冲击波速度场重建问题。迭代终止修正条件若只是满足给定的迭代次数或终止修正值与初始值的误差精度，迭代结果会出现局部收敛的情况，本文的迭代终止条件采用修正后的到达时间与初始到达时间的估计误差小于0.1%，图5为重建初始模型。

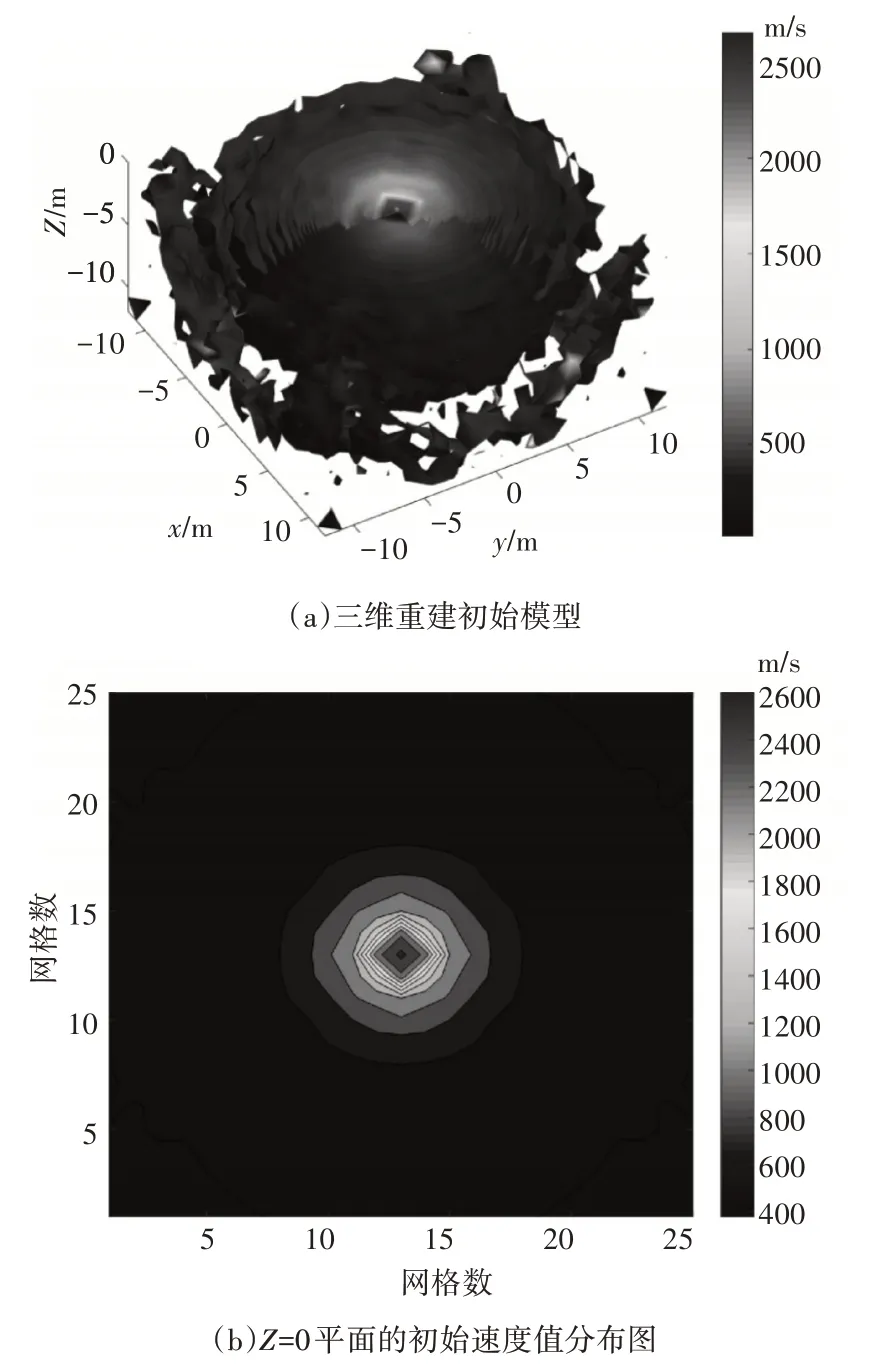
图5 三维冲击波重建初始模型

三种方法分别迭代300 次进行反演重建，三维重建结果和Z=0平面的速度值分布如图6所示。

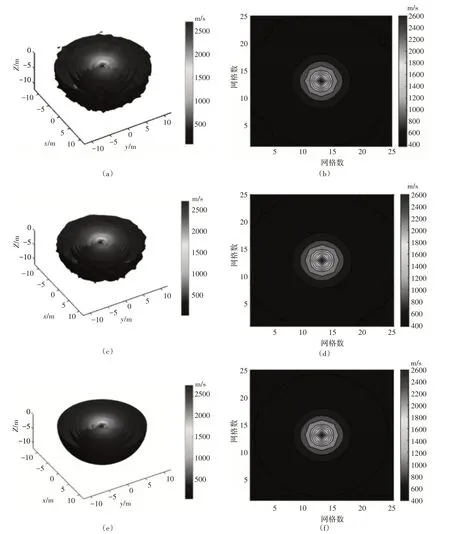
图6 三种算法分别迭代300次的重建结果

图6（a）～（b）分别为ART 迭代算法的三维重建结果和Z=0平面的重建速度分布；图6（c）～（d）分别为SART迭代算法的三维重建结果和Z=0平面的重建速度分布；图6（e）～（f）分别为TV-DL 迭代修正算法的三维重建结果和Z=0平面的重建速度分布。

由图6可以看出，与ART 算法和SART 算法的三维重建结果相比，在重建区域边缘采用本文方法进行的三维重建结果与采用传统迭代算法的三维重建结果相比更为光滑，为了更直观地观察三种方法对于边缘噪声的抑制情况，本文观察了三种重建结果的Z=0 平面的速度值分布，观察比较图6（b）、（d）、（f）可以明显看出，在有效抑制边缘噪声问题上，TV正则化具有较大优势。

为了客观阐述以上三种算法对于重建区域的重建精度，本文将采用相对误差（RE）和均方根误差（RMSE）作为重要评价参数，RE一般用来客观评价三种方法的重建速度模型与初始速度模型在一个速度重建区域范围内的各网格之间的实际重建的效果，RMSE 一般用来客观评价一个整体区域内的实际重建结果与重建初始模型结果的偏离的程度，值越小，表明重建结果越接近实际情况。三种算法重建结果的RE曲线见图7。

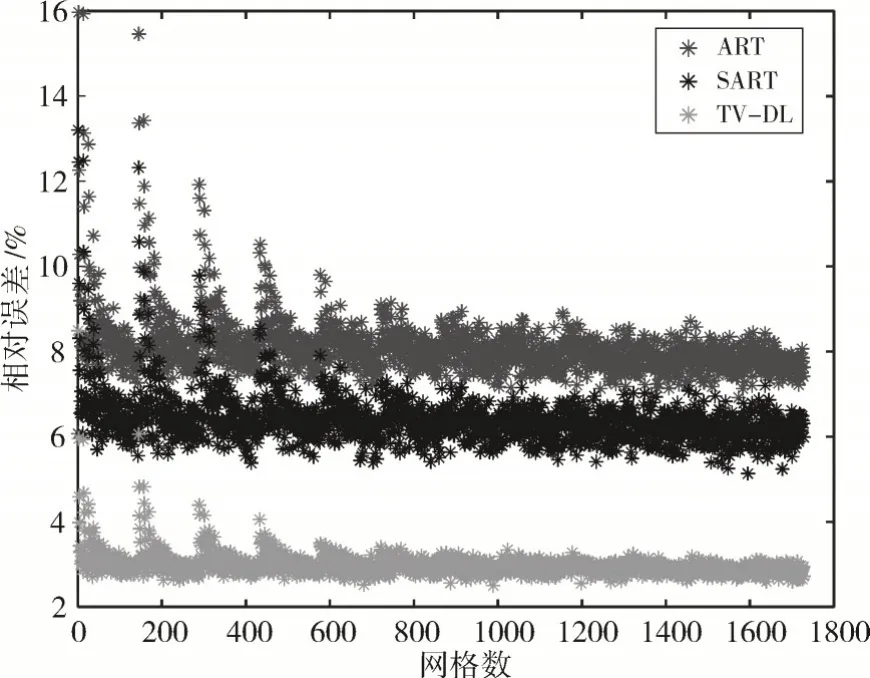
图7 每个网格内速度的相对误差

图7为三种迭代算法重建后的速度与初始速度在重建区域内的1728 个网格中的相对误差，可以明显看出，在重建区域内，相对误差曲线呈周期性衰减，究其原因是重建网格的划分是逐层排序共记12 层。由图7可看出曲线衰减大致分为12 段，爆炸冲击波场在近场区超压值变化极快，与远场相比，重建误差大，因此，误差曲线呈分段衰减的趋势。在图7中，TV-DL算法的相对误差基本能保持在3%左右，与ART 算法相比，降低了5%左右，与SART算法相比，降低了3%左右。进一步用均方根误差来作为重建后整体误差，三种算法的RMSE 值如表1所示。

表1 重建结果的均方根误差

已知重建区域整体的速度范围大约在400m/s～3000m/s，由上表可知，三种算法整体的速度场重建的总误差依次为45.81m/s、38.79m/s、9.85m/s，即本文方法的整体重建效果显著优于ART 算法和SART 算法。通过分析综合运用以上两个参数，可以进一步直接证明本文提出的方法在区域重建方面更具优势。从数据整体重建的效果来看，TV-DL方法所获得的结果与真实的模型小，三维重建的误差远比其他两种算法小，综合分析来看，在三维峰值超压场重建模型的实际开发应用层面上，TV-DL方法的获得三维重建模型效果最优。

5 结语

为得到爆炸冲击波三维空间分布情况，并达到良好的可视化效果，首先本文深入研究了冲击波二维走时层析成像的原理，在二维走时层析成像模型的基础上，根据射线追踪理论，构建起了三维冲击波峰值超压强场的重建模型；然后，运用了压缩感知算法在稀疏约束方面的优点，给出了一种基于TV-DL 冲击波超压强场迭代修正算法；开展了模拟试验，并对比了传统重构算法ART、SART 和TV-DL 的重构结果。对试验结论分析表明，本文首次提出的三维射线走时层析成像方法已经能够初步实现三维冲击波超压场重建。TV-DL 修正代数重建精度的相对误差基本保持在3%左右，与ART 算法相比，降低了5%左右，与SART 算法相比，降低了3%左右，本文仅对冲击波三维重建进行了仿真实验，但由于实际传感器布设困难，后续会继续研究在满足重建精度的前提下减少传感器个数，实现冲击波三维重建。