远海作战预警机在战斗机掩护下的威胁规避方法*
赵 卿 冯亚军 尹康银 李国强 任 川
(1.空军预警学院 武汉 430019)(2.95668部队 昆明 650200)
1 引言
预警机作为航空兵海上作战的重要情报来源和重要指挥中枢[1],是空中作战力量的重要组成部分,在我军海上作战中发挥着至关重要的作用[2]。远海作战中,地面雷达受地形限制,只能部署在少数几个岛屿担负对空警戒任务[3],虽然舰艇雷达可以随水面舰艇的机动部署发挥一定作用,但是受地球曲率影响,舰载雷达和地面雷达的低空探测性能将受到限制[4],因此,预警机是远海作战预警监视和指挥控制的重要力量[5]。预警机作为高价值目标,必将成为敌方重点打击的对象[6]。远海作战与内陆作战不同,通常难以常态化部署密集的地面防空火力[7],因此,战斗机掩护将成为确保预警机飞行安全的主要依托[8]。
预警机在远海执行任务时,由于缺少防空火力的掩护,为了提高预警机空中防护能力,歼击机应当采用间接掩护方式前出设置掩护空域,拓展对敌机的拦截纵深。通常在预警机探测范围内、飞行空域外靠近敌方可能进攻方向一侧,设置歼击机掩护区域[9]。不管是进攻作战还是防御作战,预警机都要事先规划好在遇到敌机威胁时的规避方案。预警机指挥员应根据当前空中态势和敌我机飞行动态,进行威胁评估,如敌空中目标对我构成威胁时,应果断按照规避方案采取紧急避险措施并引导掩护歼击机前出进行拦截。
当预警机在空执行任务时,如发现敌机目标以高速或者高空飞行形式直接飞向预警机,此时应确保预警机与威胁目标保持足够的安全距离,以争取预警机留有足够的时间向后方飞行逃逸。而当敌机目标与预警机的距离小于安全距离时,为确保预警机自身安全,预警机必须采取威胁规避措施,同时指挥引导担负掩护任务的战斗机对敌机进行拦截。
2 预警机威胁规避分析模型
假设t0时刻预警机和担负掩护任务的歼击机的相对位置如图1 所示,预警机和歼击机都按照双平行线航线飞行,且飞行速度和相对位置始终保持一致,预警机的位置在O点,歼击机位置在F点。此时,若敌方歼击机位置出现在S点,且航向直接指向预警机,则预警机指挥员需要密切监控敌机的飞行动态,确保预警机和敌机保持一定的安全距离。
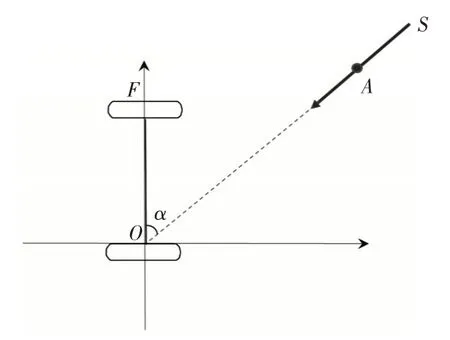
图1 战斗机掩护预警机示意图
假设敌方歼击机飞至A点后,预警机必须采取逃逸动作,同时指挥歼击机前出对敌机进行拦截,OA的长度为预警机最小安全逃逸距离。为增加敌机的追击距离,提高预警机的逃逸成功率,预警机的逃逸方向应当与敌机的飞行方向一致。为了方便计算,建立以预警机位置O为坐标系原点,以预警机逃逸方向和敌方歼击机追击线路为横轴的直角坐标系(如图2 所示)。预警机在敌歼击机飞至A点后首先转变航向至敌机追击方向,待航向与敌机一致后再向E点方向逃逸,我歼击机采用前半球截击的方式拦截敌歼击机[10]。由于歼击机的机动性远高于预警机,所以本文将歼击机的反应动作进行忽略,假定歼击机向着敌机前方某点B飞行,敌机飞至B点时,我机飞至C点,此时敌机刚好处于我歼击机空空导弹的攻击射程内。在我歼击机发射空空导弹后,敌机在击落前飞至H点,此时预警机飞至E点,令H点刚好处于预警机的最近截击线上,才能确保敌机发射导弹攻击预警机前被我方空空导弹击中。
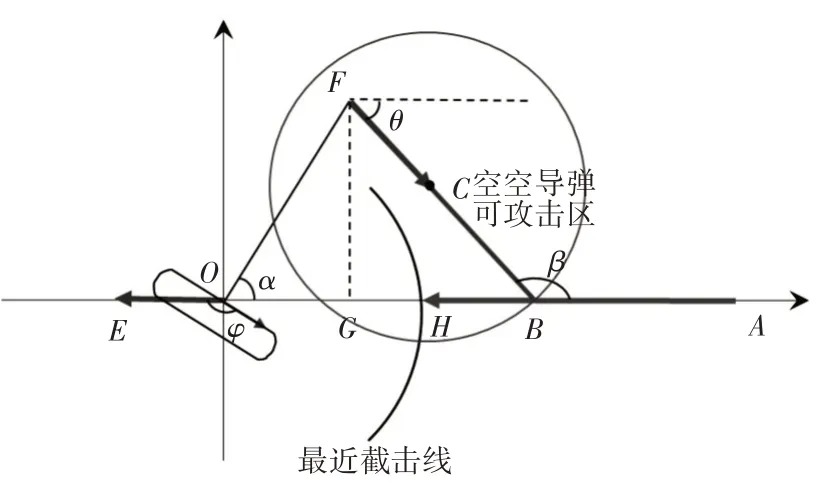
图2 敌机攻击预警机示意图
3 预警机安全逃逸距离计算
图中α角为敌机飞行方向相对预警机和我方歼击机初始位置的夹角,β为歼击机相对敌机的拦截阵位角[11],可以求得图中角θ=180°-β。DAB为敌机在被我歼击机导弹锁定前的飞行距离,DFC为我机前出拦截敌机后,到发射空空导弹前的飞行距离,DOF为我歼击机到预警机之间初始距离。设预警机飞行速度为V预。我方歼击机的飞行速度为V我,敌方歼击机的飞行速度为V敌,敌机由A 点飞至B点时所用的时间为T,我方空空导弹的速度为V导,敌方空空导弹的射程为D敌,我空空导弹的射程为D我,可以得出DBC=D我,DEH=D敌。需要计算的变量为O点到A点的距离DOA、β。不考虑距离截获概率、速度截获概率、角度截获概率和空空导弹杀伤概率的影响,可以求得:
敌机飞由A点飞至B点的距离为
我机由F点飞至C点的距离为
敌机由B点飞至H点的距离可近似的由我空空导弹飞行时间和敌机飞行速度计算得出:
预警机转弯半径R转可由转弯坡度和预警机的飞行速度求出,β为预警机的转弯坡度,g为重力加速度,计算R转时应将V预的单位转换为m/s[12]。
如图2 所示,考虑最坏的情况,假设敌机飞至A点时,预警机正与敌机相对而行,敌机航向与预警机和我方歼击机位置的夹角为α,可以确定预警机航向的需要顺时针旋转φ=90°+α,才能使预警机与敌机航向一致。通过式(4),可以计算得到预警机的转弯时间T转:
代入R转后得到:
预警机在转向完毕后才能由O点向E点飞行,由O点飞至E点的距离可由敌机飞行的总时间和预警机的飞行速度求出:
根据三角函数公式,可得:
从图中可以得知,DAH+DEH=DOE+DOA,由式(3)、(6)、(7)可得:
由式(8)、(9)、(10),可以求得DOA、T和θ,由β=180°-θ可求得拦截阵位角β。
若角α为自变量,那么可以由式(8)、(9)、(10)求得角α和DOA的关系式,以此来建立α和DOA在极坐标系下的关系图,得到预警机在所有方位的最小安全逃逸范围图。但是计算时预警机需要转向角度φ的值会随着α的值变化而出现区间性变化。
需要说明的是,当敌机的航线与我歼击机空空导弹攻击范围有交点时,即敌机必定会在飞行中的某一时刻出现在我歼击机的攻击范围内,此时,我歼击机只需在现有空域盘旋待战,预警机无需组织逃逸动作。如图3 所示,预警机在原点O,歼击机在预警机前方F点处担负掩护任务,我歼击机空空导弹的射程形成以F点为圆心,空空导弹射程D我为半径的圆,由原点O引出两条与该圆相切的直线。
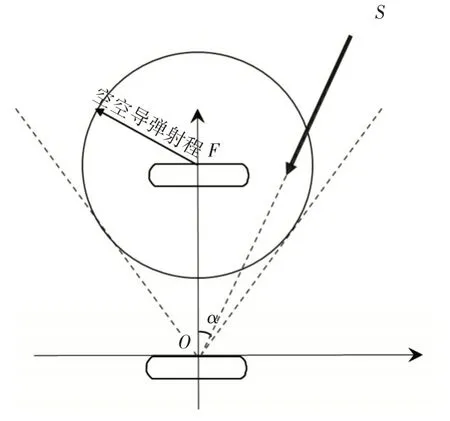
图3 敌机有效攻击路线示意图
4 仿真与验证
某时刻,预警机在战斗机掩护下执行巡逻任务,预警机和战斗机都采用双平行线航线,且航线参数保持一致,战斗机的掩护阵位距离预警机阵位100km。敌机携带空空导弹欲从α=60°方向对我预警机实施攻击(图4 所示),量化分析条件如表1所示。求预警机的安全逃逸距离DOA和我歼击机的拦截阵位角β,以及当α未知时预警机的安全逃逸范围。
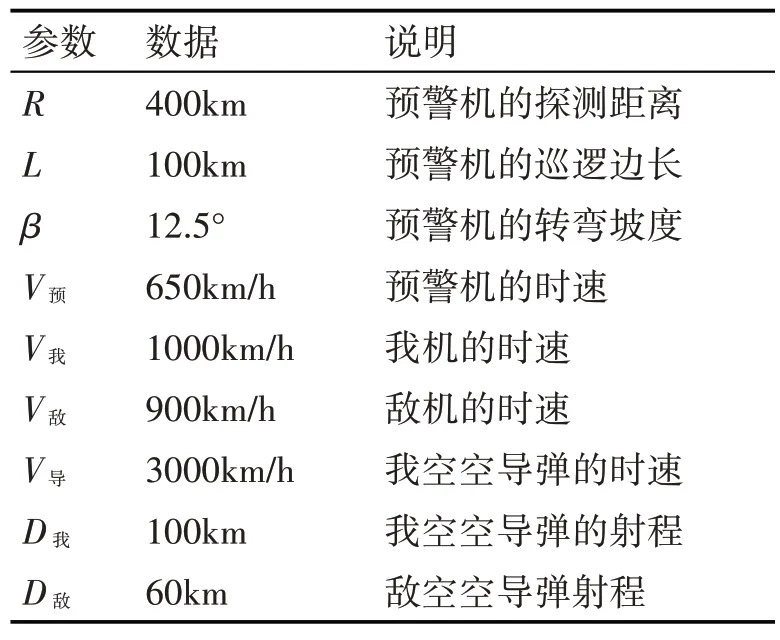
表1 量化分析条件
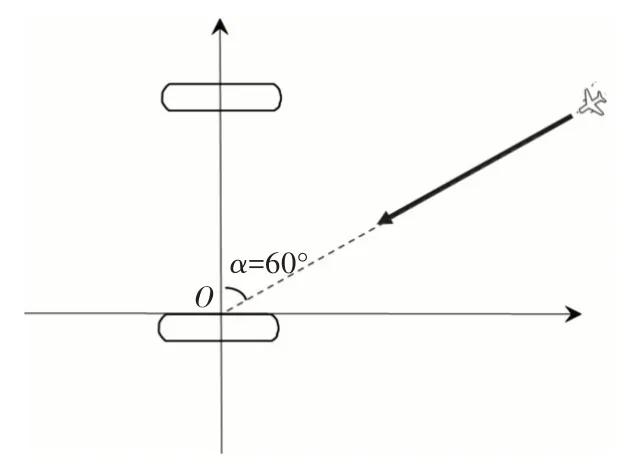
图4 敌机攻击路线
由式(4)可以得到R转=15km ,再由式(8)、(9)、(10)可以计算得到当α=60° 时,DOA=116km,β=112.4°。
当α未知时,通过Matlab软件仿真得到预警机在所有方位的安全逃逸范围。如图5 所示,蓝色实线为预警机在所有方位的安全逃逸范围,红色圆形实线为我歼击机空空导弹可攻击范围,若敌机从两条虚线范围内进攻,则敌机飞行航线在我掩护战机的攻击范围内,此时预警机无需采取规避措施。
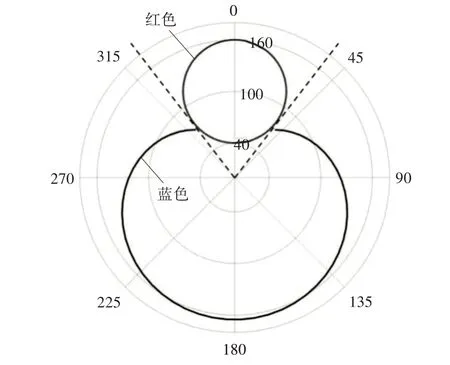
图5 预警机的安全逃逸范围仿真结果
5 结语
本文提供了一种预警机在战斗机掩护条件下对敌机威胁进行规避的分析方法,通过对比分析预警机和敌我战斗机的战术动作,建立了量化分析模型,得到了预警机与敌机之间的安全距离边界。对于分析模型仍有许多有待优化的地方,这将在后续学习中进行研究。

