基于PSO-SVDD的齿轮箱故障诊断*

骆东松 薛 鑫

（兰州理工大学电气工程与信息工程学院 兰州 730050）

1 引言

运行可靠始终是旋转设备的第一安全底线，也是企业发展的根本保障。齿轮箱作为旋转设备中较复杂的结构部件，工作运行环境复杂，故障种类繁多，在服役期内，受径向和轴向负荷突变，引起严重损伤，直接影响设备的安全运行，甚者引发安全事故。因此，设备的在线检测和故障判断对齿轮箱的维护和或更换具有重大的变被动为主动的战略意义。轴承箱作为复杂机械部件，故障数据获取存在困难，且不同设备之间故障数据存在较大差异，导致常用的故障监测方法因故障数据的缺乏以及系统开发的困难程度，成为制约齿轮箱设备状态监测的一个重要原因。

支持向量数据描述（SVDD）是对支持向量机（SVM）的一种延伸。与传统的SVM 算法不同，SVDD 是一种单值分类方法，就是可以对某一类数据进行分类，SVDD 的支持向量决定的最小超球体能够包含被分类数据中的绝大部分，对样本依赖度小，不会出现过拟合，具有计算速度快、鲁棒性强、适合小样本数据的处理，更适合在嵌入式设备中的应用，同时在文本分类、垃圾邮件识别、图像分类、蛋白质分类中被广泛应用。

本文提出了一种经PSO 优化后的SVDD 算法，该算法在本文用来对齿轮箱故障进行诊断。利用经典的振动信号处理方法，对不同故障状态下齿轮箱振动数据进行降噪与特征参数的提取，用SVDD算法将处理后的振动数据先求取支持向量，然后利用支持向量求取最小超球体，进而求取特征参数所存在的特征域，构造能够表征罗茨风机齿轮箱在不同故障下运行状态的特征域，对相关结果进一步分析总结出本文提出的方法是可行的［1］。

2 支持向量数据描述（SVDD）

SVDD 早期首先是由TAX 等人结合了SVM 思想提出来的，是低维空间向高维空间的延伸。在机械故障诊断、图像检测等方面得到了广泛应用，因为有了核函数的引入，导致SVDD 的性能将会直接受到核参数选择的影响，要想达到理想的效果只有选择较为合适的核参数才能实现［14］。SVDD是一种单值分类算法，可以对单组数据进行空间向量描述。

最小超球体示意见图1，其中：a 是最小超球体的球心，R 是最小超球体的半径。假设样本集空间中包含N 个样本xi（i=1，2，…，N），在实际工程当中，由于外界噪音的干扰，在构造超求体时，会将一些奇异值包含在内，使得分类准确率下降或构造的超球体并非为最小超球体。为减少奇异值的影响，引入松弛变量ξi［2］，对应优化问题的数学描述为

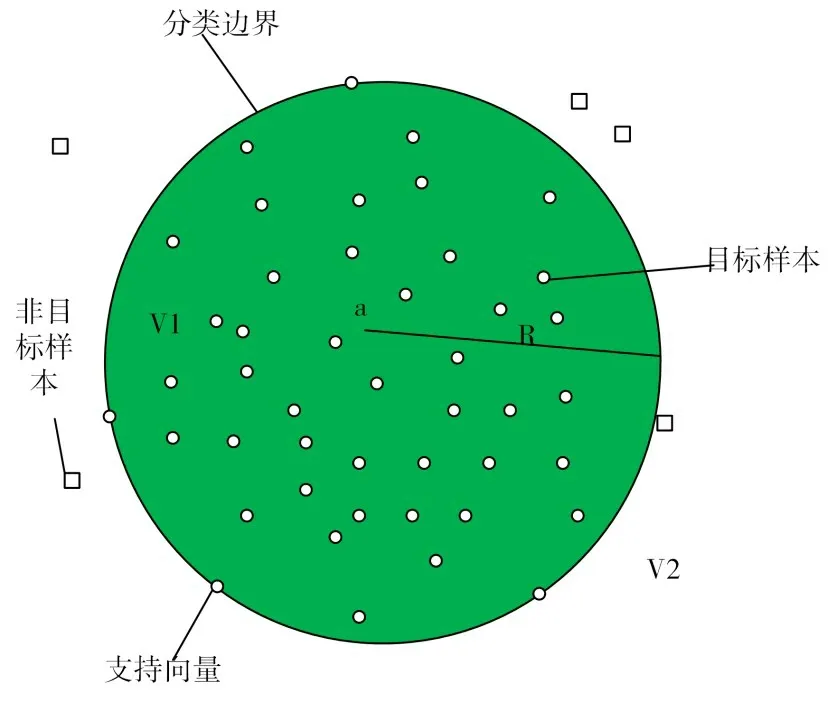
图1 二维空间超球体示意

式（1）中：C 为惩罚因子，用来平衡目标样本和非目标样本的比例。

为方便求解，引入拉格朗日乘子。

式（2）中：αi≥0，βi≥0 为引入的拉格朗日乘子。将LP(a，R，α，β)由L代替，则式（2）的对偶形式为

对该优化问题进行求解可以得出αi的值，当αi≠0 时，其对应的样本即为支持向量［2］，超球体的球心与半径的求解公式为

对于任何一个测试样本点z，如果满足：

通常情况下，在低维空间中数据的分布不会呈球状，故引入径向基核函数K(xi·xi)代替式（3）中的内积运算，将低维空间中的非线性问题转化为高维空间中的线性问题［15］，求解过程变得简单。即

测试样本z为目标样本只需满足：

3 线性变换粒子群优化算法

粒子群优化算法（Particle Swarm optimization，PSO）又翻译为粒子群算法。PSO 初始化为一群随机粒子（随机解），然后通过迭代找到最优解。假设n 维空间中第i 个粒子的位置和速度分别为Si=(Si1，Si2，…Sid) 和Vi=(Vi1，Vi2，…Vid) ，为了找到全局最优解，算法进行迭代计算，每次迭代计算中，粒子通过跟踪个体最优解Pbest，Pi=(Pi1，Pi2，…Pid)与全局最优解（gbest）来更新自己［14］。

粒子通过式（8）更新自己的速度和位置：

其中：ω为惯性权重因子，c1和c2为大于0 的学习因子，r1和r2为随机数，其分布区间为0～1。

在PSO 算法中ω是最重要的可调参数，t和t+1 分别代表迭代次数当前值和下次值。由于惯性权重越大越有利于PSO算法跳出局部极小点［14］，防止算法进入局部循环，提高算法算法收敛速率，采用可变化的权重因子，权重因子ω在定区间内进行变化，以适应不同时期权重因子的最优值。ω随算法迭代次数的变化公式为

其中：ωmax-ωmin表示权重因子的取值空间，t代表当前迭代次数，tmax代表最大迭代次数。

优化PSO 算法的参数组[K，α]，将其初始种群数量初始化为10，最大迭代次数初始化为30，学习因子c1和c2都初始化为1.5，根据图2 可以看出PSO 在寻求最优解的过程中，局部极小值EP随种群进化，当迭代次数为4时，算法收敛。

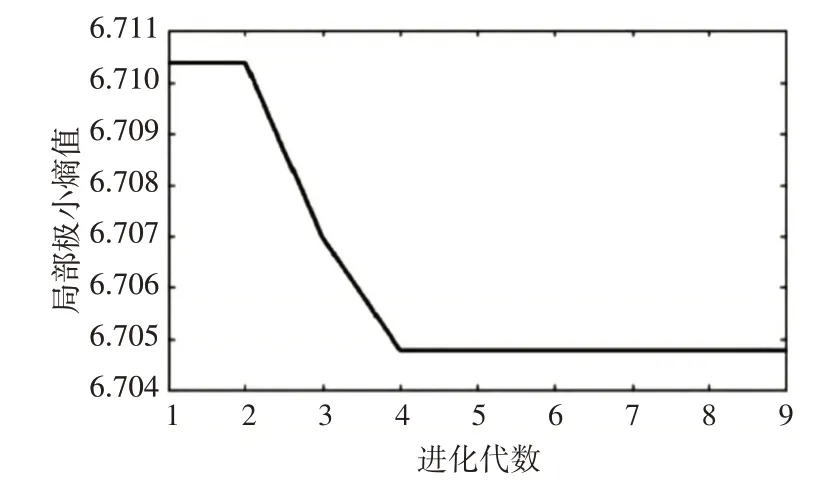
图2 PSO种群进化

4 基于PSO-SVDD的故障诊断过程

针对某热源厂大型罗茨风机减速齿轮箱故障诊断中存在的响应时间长，响应精度低等问题。本文提出将粒子群算法PSO 与支持向量数据描述SVDD 相结合，通过两种算法的结合，发挥各算法的优势，而后对齿轮箱进行故障诊断。故障诊断过程如图3所示。

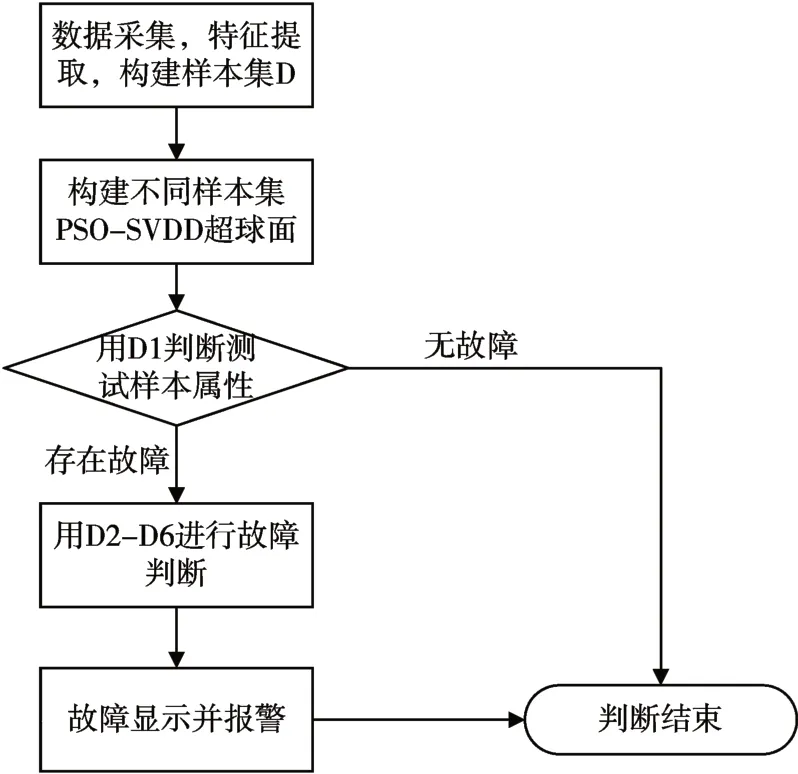
图3 故障诊断过程

步骤1：对厂区罗茨风机运行振动数据进行采集并进行特征提取，样本数据集包括：正常样本数据集D1、点蚀样本数据集D2、点蚀磨损样本数据集D3、断齿样本数据集D4、磨损样本数据集D5、断齿磨损样本数据集D6。

步骤2：利用优化后的PSO-SVDD 算法对样本数据所包含的正常样本和已知故障类型样本数据构建超球面，用做后面两步故障类型判断的依据。

步骤3：利用数据集D1构建的故障诊断模型对测试样本进行第一轮诊断，判别式为函数式（7）。如果满足则说明罗茨风机运行正常；反之，则说明样罗茨风机存在故障。

步骤4：第一轮诊断后部分测试数据显示该齿轮箱存在故障，对存在故障信号的测试数据进行第二轮诊断。分别将测试数据用数据集D2构建的故障诊断模型进行故障诊断，判别式依然为函数式（7），若输出有故障，则实际数据并无该故障。同理，依次用不同故障样本数据构建的超球面对测试数据进行故障诊断，当输出显示无故障，则测试数据存在此类故障，并进行故障显示。

5 试验分析

本次设计应用于某热源厂2#罗茨风机的变速齿轮箱中，模型训练数据集通过设计的下位数据采集器采集得来，设备额定功率为75KW，额定转速为800r/min，驱动端轴承型号为SKF6205 数据集采集转速为额定转速的70%，即罗茨风机的变频器频率为35Hz，振动信号采样频率为12KHz，16 位AD采样，采样时长8s，将采集到的数据集划分为60组，其中40 组作为训练数据，取SVDD 算法的拒绝率为百分之一，径向基核函数的σ参数为5，进而求出支持向量、球心和半径。其余20 组作为测试数据。齿轮箱状态包括正常、点蚀、点蚀磨损、断齿、磨损以及断齿磨损。经PSO-SVDD诊断后得到的故障诊断结果如图4所示。

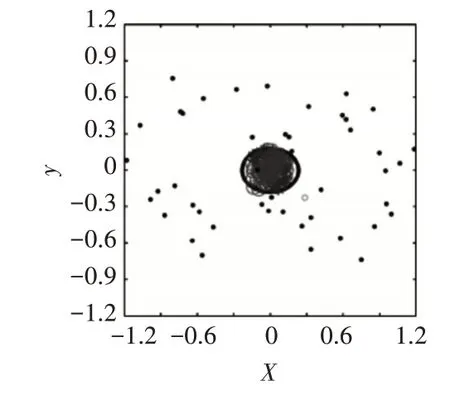
图4 PSO-SVDD算法诊断结果

传统的SVDD 算法，作为典型的单值分类器，其缺点也是显而易见，通过该模型只能简单判断出设备在运行过程中是否出现故障，但对于出现故障的具体类型却不能够做出判断，即使如此简单也已经对事故的预防起到了重大的作用。本文提出的通过将单一故障样本假设为正常样本进行的第二次故障诊断，通过逻辑运算，可以很好地解决SVDD 算法因其单值分类这一特性所造成的无法对机器的故障类型做出更准确的判断这一缺憾，完成了齿轮箱相应的故障诊断，此法亦可用于其他部件故障诊断中。

6 结语

齿轮箱的故障诊断在大型风机系统中是不可或缺的一环，但仅凭单一的传感器及传统的齿轮箱故障诊断方法很难准确诊断出具体故障类型，影响设备安全运行以及企业的经济效益。

本文提出的利用PSO-SVDD 单值分类器对采集到的振动数据进行两轮诊断，通过对结果的逻辑运算，分析出齿轮箱故障。在用SVDD 模型进行故障诊断时，核函数的选择是重中之重。本文选取的径向基核函数相比于其他核函来说较为简单，编程难度较低。试验结果表明，与传统的旋转设备故障诊断技术相比，该诊断算法更加简单，对硬件要求更加简单，适合便携式故障监测设备开发所需要的智能诊断算法。

本课题由于传感器安装位置、传感器误差和特征提取误差导致的数据间的冲突忽略不计。