基于OpenCV-Python的土壤颗粒动态休止角试验*

周鹏飞，蒙贺伟，2，3，梁荣庆，张炳成，坎杂，2，3

(1. 石河子大学机械电气工程学院,新疆石河子,832000; 2. 农业农村部西北农业装备重点实验室,新疆石河子,832000; 3. 绿洲特色经济作物生产机械化教育部工程研究中心,新疆石河子,832000)

0 引言

新疆是中国的棉花主产区,受地理环境条件影响,棉花普遍采用覆膜种植[1-2]。棉花收获期后田间铺设的残膜经机械化回收,其中夹杂裹挟大量土壤,致使残膜初清理及资源化利用难度大[3-5]。针对该类土壤的物料特性进行研究,是设计开发相关筛分、输送机械的基础,对解决残膜杂质分离问题具有重要意义。

在农业机械实际作业中,土壤颗粒大多处于快速运动的动态变化中,如筛分作业等,静态休止角不足以充分表征土壤颗粒的流变特性,因此需针对动态休止角进行研究。土壤动态休止角的传统测定方法是使用测量仪器对土壤运动时形成的休止角进行测量,这种方法误差较大,难以满足实际研究需求。近年来,随着计算机技术的不断发展,应用于研究的手段和途径也在不断扩充和丰富,相关学者积极探索利用计算机图像处理技术辅助研究的途径[6]。向伟等[7]采用Matlab软件对南方黏壤土静态休止角单侧图像进行处理,测得了该类土壤的静态休止角。王涵斌等[8]利用基于Sobel算子的计算机图像处理技术获取了沙壤土静态休止角边界轮廓,通过线性拟合实现对沙壤土静态休止角的测量。戴飞等[9]通过将采集的土壤静态休止角图像导入CAD软件,利用内置标注工具实现对土壤静态休止角的测量。田辛亮等[10]利用Matlab软件对玉米秸秆—土壤混料堆积图像进行处理,提取边界轮廓并进行线性拟合,获得了该混料的静态休止角。鹿芳媛等[11]将采集图像导入In-Sight Explorer软件,利用该软件的几何测量模块实现对水稻芽种静态休止角的测量。刘凡一等[12]依据k均值聚类算法,获取了麦粒静态休止角和动态休止角的边界,经线性拟合完成麦粒静、动态休止角的测量。由上可知,将计算机图像处理技术与基础试验研究相结合从而提升研究的准确性和便捷性,已然成为一种发展趋势。

本文以新疆棉田机收膜杂中的土壤为主要试验对象,搭建了一套土壤动态休止角测量装置,采用基于OpenCV-Python的计算机图像处理技术对图像进行有效处理,获取不同转速下的土壤动态休止角,对结果进行对比分析,匹配适宜土壤动态休止角测量的最佳转速,为同类散粒物料动态休止角测定以及流动特性研究提供参考。

1 动态休止角测量装置搭建与图像采集

1.1 动态休止角测量装置搭建

本文采用转鼓法[13]对土壤动态休止角进行测量,搭建的土壤动态休止角测量装置如图1所示。土壤物料装填于空心圆筒内部,空心圆筒前端设有透明盖板,且通过螺栓进行紧固连接,以便于土壤装填;空心圆筒后端与电机输出轴相连,并保持空心圆筒与电机输出轴在同一轴线。工作时,空心圆筒水平放置于4个对称布置的托轮上,在电机的驱动下绕自身轴线旋转。土壤在自身重力、颗粒间摩擦力和离心力的共同作用下,沿空心圆筒内壁进行倾落运动。

1.2 图像采集与摄像头标定

数字图像采集环节采用CMOS摄像头(分辨率:1 280 像素×720像素;帧率:60 fps),摄像头水平固定于三脚架,并与空心圆筒保持在同一轴线上,通过USB接口实现与计算机间的通信,并由OpenCV摄像头驱动程序启动。所采集的数字图像在计算机端进行后续处理和分析,处理流程如图2所示。

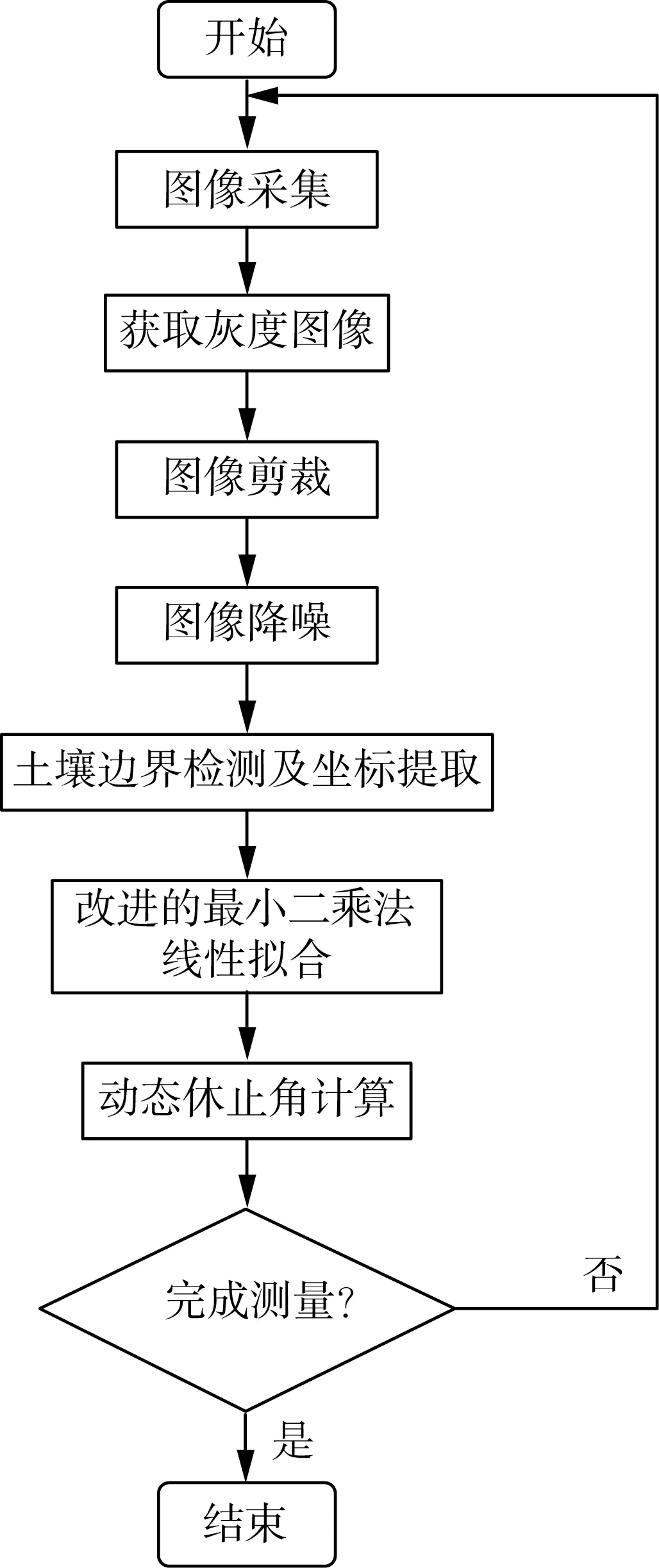
图2 土壤动态休止角测量流程图

由于光线进入摄像镜头时会产生畸变,从而导致进行图像处理获取特征信息时出现偏差,对成像造成直接影响。因此,在对采集的图像进行处理前,需对摄像头进行标定。本文采用Zhang[14]提出的基于黑白棋盘格的摄像头标定方法(简称张氏标定法),该方法具有精度较高、便于操作等优点。根据张氏标定法,选取平面二维12×10黑白相间的棋盘格为标定板,单个方格尺寸为20 mm×20 mm,其内角点数为11×9,通过OpenCV-Python库函数驱动摄像头获取不同角度的图像共计9张,并对图片进行角点检测并进行标识,从而确定角点坐标,其检测结果如图3所示。利用OpenCV-Python库函数对摄像头的内参数矩阵进行求解,利用非线性最小二乘法估计畸变系数,使用极大似然估计法优化参数,解得摄像头的内参数矩阵Q如式(1)所示,畸变系数K如式(2)所示。

图3 角点提取图像

(1)

K=[-0.0431.032-0.009-0.011-6.541]

(2)

2 基于OpenCV-Python的图像处理

2.1 图像预处理

本文主要针对土壤在空心圆筒内运动时的动态休止角,而在图像采集过程中难免会产生冗余信息,对所采集图像进行预处理可以有效剔除不需要的图像信息、保留某些对于后续处理有重要作用的图像特征。

1) RGB图像是3通道图像,灰度图是单通道图像,通过将RGB图像向灰度图转换,可在保留图像梯度信息的前提下,提高运算速度,缩短处理时间。灰度图像与RGB图像之间的映射关系如式(3)所示。

Gray(x,y)=T(R(x,y),G(x,y),B(x,y))

(3)

式中:Gray(x,y)——图像灰度值;

R(x,y)、G(x,y)、B(x,y)——各通道分量;

T——图像灰度值与各通道分量间的函数关系。

本文采用OpenCV库函数对图像进行灰度化处理,处理后的图像如图4所示。

图4 灰度图

2) 土壤动态休止角形成于空心圆筒内部,空心圆筒外部的图像信息对本文无实际意义。将无用信息剔除,保留所需图像特征,可提高图像处理效率。以空心圆筒内壁为边界,将图像进行圆形裁剪,保留空心圆筒内图像特征信息。具体实施方式是:(1)利用OpenCV内置cv2.HoughCircles()函数通过霍夫变换确定空心圆筒的半径与圆心所在位置;(2)根据空心圆筒半径与圆心位置剪切去除其余图像,保留圆内图像信息,处理后的图像如图5所示。

图5 圆形裁剪后的图像

2.2 图像降噪

图像噪声是指存在于图像数据中的不必要的或多余的干扰信息。由于在图像采集或者传输过程中受到电磁环境、光照条件及各种随机信号等的影响,采集的图像将存在一定噪声,直接对后续处理结果的准确性产生影响。对图像进行降噪处理,可在一定程度上还原图像信息,降低噪声带来的不良影响,满足图像后续处理需要。根据统计分布特征,图像噪声主要可以分为高斯噪声、泊松噪声和脉冲噪声等。针对不同噪声,常用高斯滤波和中值滤波等方法对图像进行降噪处理。利用该类方法进行图像降噪时,会以损失部分图像特征信息为代价。为避免降噪处理对图像特征信息的影响,本文采用三维块匹配滤波(Block-matching and 3D filtering,BM3D)算法对图像进行降噪处理。BM3D算法是一种基于图像块间相似性进行降噪的三维滤波算法,实现过程可分为基础估计阶段和最终估计阶段两个阶段,而每个阶段可以分为块匹配、协同滤波和聚集三个部分,其具体实现过程如下[15-16]。

1) 在整幅图像中搜寻符合参考块的相似度要求的匹配块,将所有匹配块组合形成一个三维矩阵,其结果可由式(4)求解得出。

SxR={x∈X:d(FxR,Fx)≤τmatch}

(4)

式中:SxR——与参考块类似匹配块的集合;

d(FxR,Fx)——参考块和匹配块间的距离;

τmatch——距离阈值;

FxR、Fx——三维滤波算法的参考块、匹配块。

2) 对三维矩阵进行线性变换,利用阈值收缩变换域的系数,做逆线性变换,从而达到降低图像噪声的目的,其过程如式(5)所示。

(5)

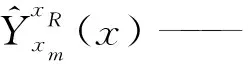
T3D——三维域变换;

T3D-1——T3D逆变换;

γ3D——硬阈值;

λth3D——三维阈值参数;

σ——图像噪声的标准差;

N1——块边长。

3) 由于同一参考块可能会存在若干估计值,导致各像素点同样会产生若干估计值。因此,需对估计值进行加权平均计算,如式(6)所示,通过该方式可得到降噪图像。

(6)

(7)

式中:ωxR——局部估计的权重;

Nhar——降噪后所有非零元素的个数。

由于无法通过主观对图像降噪效果进行定量评价,因此需借助客观手段对原始图像和降噪处理后图像进行对比分析,根据结果确定降噪效果[17]。峰值信噪比(Peak signal-to-noise ratio,PSNR)和结构相似指数(Structural Similarity index,SSIM)是目前常见的评价图像质量的参数。峰值信噪比是评价图像噪声水平的参数,其计算公式如式(8)所示,结果取值范围为[0,100]。当使用峰值信噪比衡量图像的质量时,其值越大,说明所使用的降噪算法对噪声的抑制效果越好。结构相似指数是评价降噪后图像与原图像相似度的参数,其计算公式如式(9)所示,结果取值范围为[0,1]。结构相似指数越大,说明降噪算法对图像特征的保持情况越好,越有利于后续图像处理对图像特征的提取。

(8)

式中:u——N×N的数字图像;

v——降噪后的图像。

(9)

式中:μx、μy——图像u和v的均值;

σx、σy——图像u和v的方差;

σxy——图像u和v的协方差;

c1、c2——为避免分母为0而引入的常数。

利用动态休止角测量装置对土壤动态休止角进行图像采集,随机选取图像10幅,经图像预处理后,采用BM3D算法对其进行降噪处理,通过对比降噪处理前后的图像,峰值信噪比和结构相似指数结果如表1所示。

表1 BM3D算法对图像降噪结果的客观评价Tab. 1 Objective evaluation of BM3D algorithm on the denoising results of experimental images

由表1可知,峰值信噪比和结构相似指数的均值分别为36.48 dB、0.88,可满足后续图像处理需求。

2.3 土壤边界特征提取

图像边界指图像中灰度或结构发生突变的位置,是图像最基本的特征,也是纹理特征和形状特征提取等图像分析的基础。本文所需提取的边界为土壤颗粒外缘轮廓,边界特征提取的准确性将会直接影响动态休止角的测量结果。目前,常见的边缘检测方法主要有Roberts、Sobel、Prewitt和Canny边缘检测[18-20]。由于Roberts算法易受噪声影响;Sobel算法获取的边缘位置偏差较大;Prewitt算法在检测过程中容易出现伪边缘,造成过分割现象。因此,本文采用OpenCV中cv2.Canny()函数对土壤动态休止角图像进行边界检测并获取土壤边界,其结果如图6所示。

图6 土壤边界提取图

3 基于改进的最小二乘法的线性拟合

针对OpenCV图像处理后所得的土壤颗粒边界,以空心圆筒圆心处为原点,水平方向为x轴,竖直方向为y轴建立坐标系,确定土壤边界各像素点坐标数据,分别利用一般最小二乘法和改进的最小二乘法对坐标数据进行线性拟合,通过对求解所得线性拟合模型进行对比分析,获取拟合度较优的土壤颗粒边界方程。

3.1 改进的最小二乘法线性拟合

最小二乘法是一种通过对误差平方进行最小化处理,根据实测数据估计数学模型中未知参数的数学统计方法[21-22]。该方法便于分析与计算,在数据处理方面应用广泛,其具体实现过程是:(1)假设存在n个样本,样本坐标分别为(pi,qi)(i=1,2,3,…,n),式(10)为该样本的拟合函数,则样本与目标函数的误差平方和为式(11);(2)对误差平方和函数中每个未知系数求偏导,令偏导数为0,求解方程;(3)将方程的解代入拟合函数,该方程即为此样本通过最小二乘法所得拟合方程。

(10)

式中:φ(q)——拟合函数;

m——拟合函数的拟合次数;

ak——拟合系数。

(11)

式中:δ(p)——样本与拟合函数的误差平方和函数。

在实际应用中,由于随机噪点和干扰点等因素的影响,使部分实测数据存在较大误差,导致求解获取的最小二乘法拟合函数偏离原始数据。为提高拟合效果,本文对最小二乘法算法进行优化改进,具体思路是通过最小二乘法对土壤边界像素点进行线性拟合,获取拟合函数后分别计算各像素点与拟合点间距离,根据拉依达准则剔除异常点,对剩余像素点再次进行最小二乘法线性拟合,获取剔除异常点后的拟合函数,尽可能提高函数拟合度,确保结果能充分反映原始数据。

改进的最小二乘法拟合步骤如下。

1) 以空心圆筒圆心处为原点,以水平方向为x轴、竖直方向为y轴,以相邻像素点间距为单位距离建立坐标系,其中,土壤边界各像素点坐标为(xi,yi)(i=1,2,3,…,n)。由于需对土壤边界进行一阶线性拟合,故在式(10)中令m=1,得拟合方程如式(12)所示,进而确定误差平方和函数如式(13)所示。

φ1(x)=a0+a1x

(12)

(13)

对误差平方和函数中每个未知系数分别求偏导,令偏导数为0,即

(14)

求解方程得

(15)

此时,误差平方和函数值最小。

2) 分别计算各像素点与拟合点间距离li(i=1,2,3,…,n),如式(16)所示。根据拉依达准则对各像素点进行判定,将各异常点剔除,获得新的土壤边界像素坐标点(xj,yj)(j=1,2,3,…,n′,且n′≤n),再次利用最小二乘法进行线性拟合,求解得剔除异常点后的土壤边界拟合函数为式(17),其中一次项系数为a1′。

li=|yi-(a0+a1xi)|

(16)

φ1′(x)=a0′+a1′x

(17)

3) 根据拟合函数一次项系数,对土壤动态休止角θ求解,得

θ=arctana1′

(18)

3.2 拟合结果分析

通过自制的土壤动态休止角测量装置采集获取土壤动态休止角数字图像,随机选取10帧OpenCV处理后图像,分别利用一般最小二乘法和改进的最小二乘法进行线性拟合,根据概率学理论对线性拟合模型分析,结果如表2所示。

表2 拟合结果比较Tab. 2 Comparison of fitting results

通常情况下,利用一般最小二乘法对数据进行拟合时,易受极端异常点的影响,从而降低所构建模型的准确性。由表2可知,相对于一般最小二乘法拟合模型,改进的最小二乘法拟合模型的决定系数R2平均提升了0.29%,均方根误差平均下降了1.74,拟合效果和精度优于一般最小二乘法拟合模型。该结果表明,改进的最小二乘法可以有效提升线性方程拟合度。

4 试验结果与分析

4.1 试验材料及仪器

试验材料取自新疆玛纳斯县北五岔镇棉田机收膜杂中的土壤,该区域地处天山北麓、准噶尔盆地西南缘,土壤以棉田深度为0～50 mm的表层沙壤土为主[23]。在试验样本采集过程中按土壤在机收膜杂中所处的不同位置分别进行随机取样,通过人工对棉田机收膜杂进行筛拣,剔除机收膜杂中残膜、棉秸秆等成分。

主要仪器设备:标准土壤筛(孔径范围:2～5 mm)、JMB-5003型电子天平(测量范围:0～500 g,测量精度:0.001 g)、Sartorius MA-45型快速含水率测定仪(质量精度:0.001 g,含水率精度:0.01%)、UT372型激光转速仪(测量范围:10～99 999 r/min,测量精度:0.04%)、自封袋。试验装置为自制的动态休止角测量装置。

针对所采集的土壤样本物料,利用Sartorius MA-45 型快速含水率测定仪测量土壤的含水率,并随机取样3次,每次取样500 g,采用标准土壤筛(孔径范围:2～5 mm)对其进行筛分,利用JMB5003型电子天平(测量精度为0.001 g)对不同粒径下土壤颗粒进行称重。测定的土壤基本参数如表3所示。

表3 土壤粒径分布及含水率统计Tab. 3 Soil particle size distribution and moisture content statistics

4.2 试验方法

试验采用自制的动态休止角测量装置进行土壤动态休止角的测定。根据土壤粒径分布测定结果,选取粒径在(0,2)区间内的土壤颗粒(图7)进行动态休止角试验。填充率过大或过小均不利于对动态休止角的观测,参照文献[24]确定本试验填充率为50%。测量时,通过步进电机调节圆筒旋转速度,并利用UT372型激光转速仪进行测量验证。将摄像头固定于三脚架上,调至水平,且摄像头与圆筒处于同一轴线。待装置运转平稳后,计算机通过USB接口获取摄像头所采集图像,利用基于OpenCV的计算机图像处理技术对土壤动态休止角进行测定。

图7 土壤颗粒

4.3 结果与分析

通过调整装填土壤后空心圆筒的旋转速度,使土壤在透明端盖的内壁上形成平稳流动的斜坡,获取斜坡和水平方向的夹角,即为对应转速下的土壤动态休止角,不同转速下的土壤动态休止角结果如表4所示。

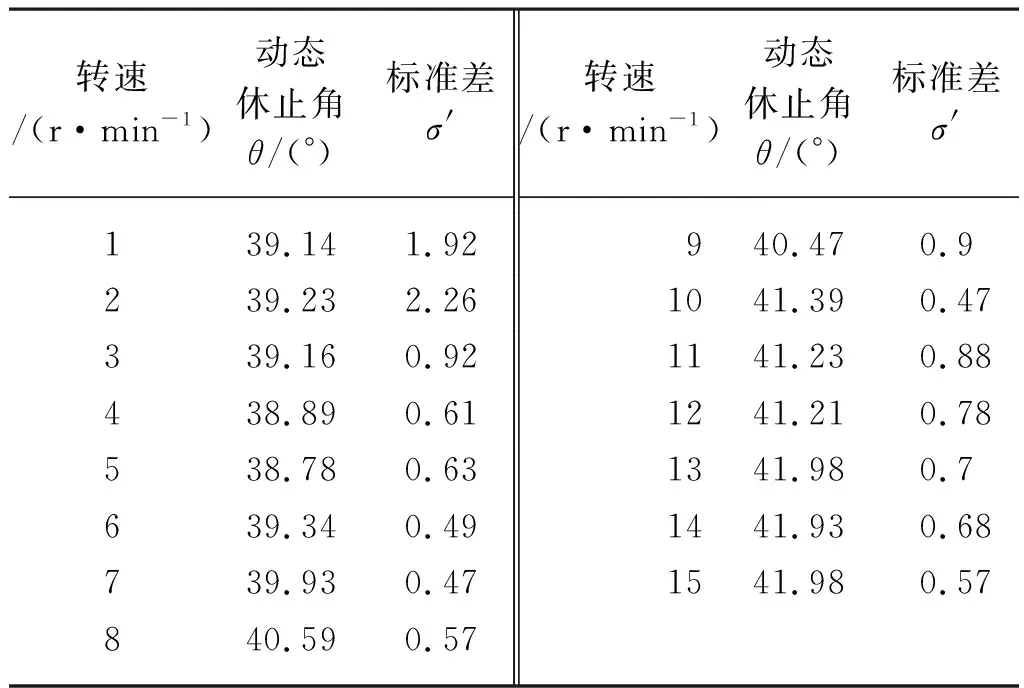
表4 不同转速下土壤动态休止角测量值Tab. 4 Measured value of soil dynamic angle of repose at different rotational speed

由表4可知,土壤动态休止角随着转速的增加呈先减后增趋势。通过对该现象产生的原因进行分析可知,当转速较低时,土壤在空心圆筒内呈间歇性滑移运动,土壤颗粒在重力、摩擦力等的共同作用下,与空心圆筒保持相对稳定,并随空心圆筒共同绕其轴线旋转,当到达某一临界高度后,土壤边界颗粒迅速滑落至颗粒间再次形成稳态,土壤颗粒的间歇运动致使所测得的动态休止角较大;随着转速的增大,土壤颗粒由间歇运动逐步转变为连续运动,故测量所得动态休止角减小;当转速进一步增大时,部分土壤边界颗粒的运动状态由滚落开始向抛落转变,抛落过程中部分土壤颗粒存在短暂的悬空,该现象致使土壤边界向外发生偏移,从而导致所测得的动态休止角增大。

目前,相关学者采用线性关系来描述转速与动态休止角间的关系,但根据转速与实测所得土壤动态休止角的变化规律发现,单一的线性关系不能很好地进行描述。本文依据不同转速所对应动态休止角分别进行线性拟合与多项式拟合,拟合所得数学模型分别为式(19)和式(20)。

y1=38.309+0.255x

(19)

y2=39.709-0.548x+0.111x2-

(4.28×10-3)x3

(20)

通过对拟合模型进行方差分析可知,线性拟合模型的R2为89.35%,均方差为0.145;多项式拟合模型的R2为95.72%,均方差为0.061,多项式拟合模型相较于线性拟合模型,拟合度更优。通过所得线性拟合模型和多项式拟合模型绘制转速与土壤动态休止角关系如图8所示。

图8 土壤动态休止角与转速关系图

根据文献[13]可知,不同转速条件下圆筒内颗粒群具有不同运动特征,而圆筒中颗粒群运动特征可通过式(21)进行预测。

(21)

式中:Fr——Froude数;

ω——转鼓转动角速度,rad/s;

R——转鼓半径,R=7.5×10-2m;

g——重力加速度,m/s2。

由梅尔曼准则可知,当10-4

(22)

式中:n*——最优试验转速;

N(σmin)——标准差最小值时所对应的转速。

由上可知,本文土壤动态休止角最优试验转速为7 r/min。

5 结论

1) 针对棉田机收膜杂中土壤动态休止角研究需求,结合基于OpenCV-Python的计算机图像处理技术,搭建了一种土壤动态休止角测量装置,通过该装置可快速准确获取土壤动态休止角,满足试验测量需求。

2) 利用OpenCV-Python进行图像处理,通过将采集图像灰度化,根据cv2.HoughCircles()函数通过霍夫变换裁切图像,去除多余图像,保留所需图像特征信息;利用三维块匹配滤波算法对获取的图像进行降噪处理,相较于原图,降噪处理后的图像峰值信噪比为36.48 dB,结构相似指数为0.88;采用Canndy算法检测并提取土壤边界像素,利用改进的最小二乘法对土壤边界进行线性拟合,从而获取土壤动态休止角。

3) 采用土壤动态休止角测量装置对不同转速下的机收膜杂中土壤动态休止角进行测定,研究分析了转速对动态休止角的影响规律并分别构建了线性拟合模型和多项式拟合模型,通过对比分析得到了拟合度较高的拟合模型,即多项式拟合模型(R2为95.72%,均方差为0.061),在此基础上,获取了土壤动态休止角最优测量转速,即7 r/min。该结果可为相关散粒物料动态休止角的测量提供了参考依据。