借助图形感悟互逆
卞书彦
苏科版数学七(下)第9章“整式乘法与因式分解”由“整式乘法”与“因式分解”两部分内容组成。这两部分内容是两种互逆变形。对于一个数学表达式,我们不仅要会顺向看,还要会逆向看,弄清其中的互逆关系,避免混淆。当我们学好整式乘法后,反过来采用逆向思维就可以学习因式分解了。
一、借助图形,类比学习整式乘法
我们学习本章时,通过第1节的“用不同方法计算电视墙的面积”,体验了单项式乘单项式的现实数学背景,根据“乘法交换律”“乘法结合律”和幂的运算性质,计算了两个单项式的乘积,得到了单项式乘单项式的法则。
对于其他整式乘法法则,包括乘法公式,我们都是通过“用不同方法计算同一图形的面积→通过归纳得出法则或公式→通过推演证实结论”这一路径展开学习的。借助图形直观,我们发现了整式乘法法则和乘法公式,感悟了数形结合思想,经历了由合情推理、演绎推理得到法则和公式的全过程,体会了数学的严谨性。这种能力中考中也有考查,例如:
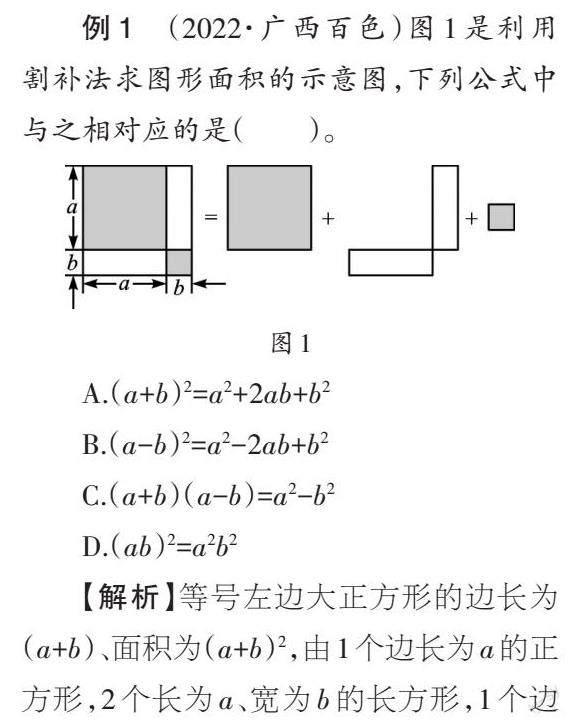
【解析】等号左边大正方形的边长为(a+b)、面积为(a+b)2,由1个边长为a的正方形,2个长为a、宽为b的长方形,1个边长为b的正方形组成。根据面积相等,即可得出(a+b)2=a2+2ab+b2。故選A。
二、利用互逆,逆向学习因式分解
教材中,“因式分解”都采用“把……反过来,就得到……”的方式呈现。我们利用单项式乘多项式,探索用提公因式法分解因式的过程,体会了单项式乘多项式与提公因式分解因式之间的联系;还将乘法公式反过来,探索出用公式法分解因式。这些探索,都发展了我们的逆向思维。我们首先要弄清因式分解的定义,才能正确分解因式,例如:
【解析】因式分解是将一个多项式变形为几个整式乘积的形式,这种变形是恒等变形。判断因式分解结果是否正确,可以用整式乘法去检查。A选项,最后运算不是乘法,因而不是因式分解,不符合题意;B选项,计算错误,不符合题意;C选项是因式分解,符合题意;D选项是整式乘法,不是因式分解,不符合题意。故选C。我们只有弄清有关公式的结构特点,才能正确运用公式分解因式。
三、知识建构,过好五关
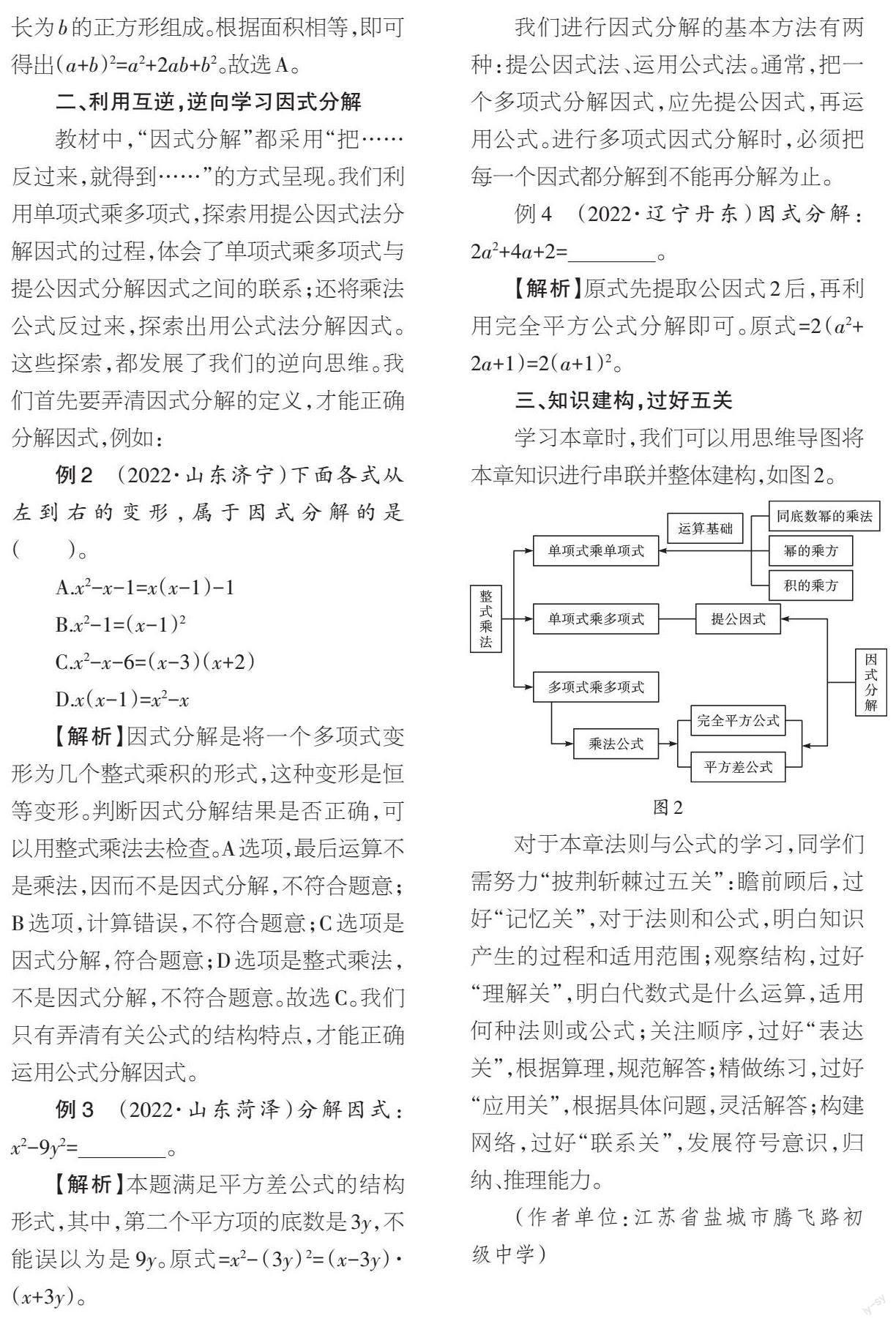
学习本章时,我们可以用思维导图将本章知识进行串联并整体建构,如图2。
对于本章法则与公式的学习,同学们需努力“披荆斩棘过五关”:瞻前顾后,过好“记忆关”,对于法则和公式,明白知识产生的过程和适用范围;观察结构,过好“理解关”,明白代数式是什么运算,适用何种法则或公式;关注顺序,过好“表达关”,根据算理,规范解答;精做练习,过好“应用关”,根据具体问题,灵活解答;构建网络,过好“联系关”,发展符号意识,归纳、推理能力。
(作者单位:江苏省盐城市腾飞路初级中学)

