基于动力学模型的烟叶变频烘烤干燥特性及收缩特性分析
陈家鼎 徐志强 赵浩宾 刘剑君 范艺宽 陈二龙 宋朝鹏 段卫东



摘要:为了给烟叶变频烘烤工艺优化提供理论依据。烘烤过程中间隔12 h取样测量记录叶片和主脉的含水率、体积,对30、40、50 Hz下烟叶的干燥特性和收缩特性进行分析,并基于8种干燥动力学模型和3种收缩动力学模型进行拟合。结果表明:(1)在试验装烟量条件下,风机频率由30 Hz增至50 Hz,对应烘烤时间缩短48 h;相同烘烤时间时,烟叶水分比大小表现为30 Hz>40 Hz>50 Hz,叶片和主脉体积比大小表现为30 Hz>40 Hz>50 Hz;(2)对不同频率下烟叶干燥特性拟合时,Page和Modified Page模型的R2均高于0.99,RMSE值均小于0.05。对不同频率下叶片和主脉的收缩特性拟合时,Weibull分布函数的R2在0.986~0.991之间,RMSE在0.034~0.043之间;风机频率由 30 Hz 增至50 Hz时,叶片的尺度参数α从106.2减至78.8,主脉的尺度参数α从133.0减至111.1。(3)在研究范围内,风机频率由30 Hz增至50 Hz时,有效水分扩散系数由1.78×10-10 m2/s增至2.65×10-10 m2/s。(4)随机挑选风机频率 40 Hz 对已得动力学模型进行验证,发现Page、Modified Page模型和Weibull分布函数的R2都大于0.99。说明Page和Modified Page模型可以作为变频烘烤中烟叶失水动力学模型,Weibull分布函数可以作为变频烘烤中烟叶收缩动力学模型。
关键词:烤烟;调制;变频;动力学模型
中图分类号:TS44+1 文献标志码:A 文章编号:1002-1302(2023)09-0186-07
基金项目:河南中烟工业有限责任公司资助项目(编号:AW202143、AW202189)。
作者简介:陈家鼎(1999—),男,河南南阳人,硕士研究生,从事烟草调制加工研究。 E-mail:1315746297@qq.com。
通信作者:段卫东,硕士,高级农艺师,从事烤烟原料加工技术研究。E-mail:xzdwd@163.com。
变频调控烘烤过程能够显著提高烤后烟叶质量[1],其作用机理是通过改变装烟室内叶间隙风速对烟叶失水速率产生影响,而烟叶的失水与收缩密切相关,相同风机频率下随着烟叶收缩程度的增大会导致叶间隙风速对应增大,进而加剧烟叶的失水[2-3]。因此,研究不同频率下烟叶的干燥特性和收缩特性,并建立相应的动力学模型,对准确描述变频烘烤下烟叶水分变化、改进变频技术和烘烤提质增效具有重要意义[4]。李生栋等研究表明,Wang and Singh模型可以很好地描述云烟87不同部位烟叶在烘烤过程中的干燥特性[5];魏硕等以K326作为试验品种进行研究,表明预凋萎烟叶主脉水分迁移和收缩速率加快[6];李昱霖等对云烟87品种进行全程30、40、50 Hz定频烘烤试验,发现38~42 ℃之间,50 Hz下烟叶的失水程度最高;38~68 ℃之间,30 Hz下厚度收缩率最高,横向和纵向卷曲度整体以50 Hz最高[7]。前人对烘烤中烟叶的干燥特性和收缩特性已有较多研究,但对不同频率烘烤时烟叶的干燥及收缩动力学模型研究相对较少。因此,本研究以挂杆为装烟方式,对不同频率烘烤时烟叶的干燥特性和收缩特性进行分析,结合8种常用干燥动力学模型和3种收缩动力学模型进行拟合,并根据菲克第二定律和Arrhenius方程计算出不同频率下烟叶的有效水分扩散系数,以期为烟叶变频烘烤工艺优化提供理论依据。
1 材料与方法
1.1 试验材料
本试验于2020—2021年在河南农业大学试验基地进行,选取同一时间建造、规格相同的气流上升式密集烤房(装烟室长为8.0 m,宽为2.7 m,高为3.3 m,装烟3层),所配备风机均为密集烤房标准轴流风机,功率2.2 kW,采用相同型号变频器进行驱动(台达VFD-M),循环风机频率可在0~50 Hz范圍内自由调节。供试品种为K326,按照当地常规优质烟叶生产技术规范进行统一管理,选取正常成熟落黄的中部叶(8~10位叶)进行试验。
主要仪器与工具:DHG-9203A电热恒温鼓风干燥箱烘箱(上海精宏实验设备有限公司)、FA2004 电子天平(上海舜宇恒平科学仪器有限公司)、BHZ-1 高精度数显厚度计(杭州蓝剑计量测试仪器有限公司)。
1.2 试验设计
参考李昱霖等的方法[7],设置低频(30 Hz)、中频(40 Hz)、高频(50 Hz)等3个风机频率处理,控制各试验烤房装烟量和烟叶成熟度基本一致,按照当地标准三段式工艺[8]进行烘烤,从烘烤开始每隔 12 h 取样1次,每次从靠近门口的中层烟杆上取20张叶片,取样后用麻布条填补空隙。
1.3 试验参数计算方法
1.3.1 干燥速率 干燥速率(vi)是指单位时间内烟叶蒸发掉的水分质量,计算公式[9]为
式中:vi为i时刻烟叶的干燥速率,%/h;ωi为i时刻烟叶含水量,%;ωt为t时刻烟叶含水量,%。
1.3.2 水分比 烘烤t时刻烟叶水分比[10]的计算:
式中:MR为t时刻烟叶的水分比;Mt为烘烤t时刻烟叶干基含水率,g/g;Me为烟叶干燥达到平衡时的干基含水率,g/g;Mo为烟叶初始干基含水率,g/g。
1.3.3 干基含水率 烟叶样品的干基含水率[11]计算参照公式(3):
式中:w为烟叶样品的湿基含水率,%。
1.3.4 有效水分扩散系数 根据菲克第二定律和Arrhenius方程[12]获得有效水分扩散系数(Deff),并由ln(MR)-t得到其斜率k0,如公式(4)(5)所示:
式中:L为干燥过程中烟叶的平均厚度,m;t为热风干燥时间,h。
1.3.5 体积比 烟叶体积的计算参考魏硕等的方法[6],将所取得烟叶叶片小样和主脉小样均视为圆柱体,其体积比VR计算公式为:
式中:Vt为烟叶样品在t时刻的体积,m3;V0为烟叶样品在初始时刻的体积,m3。
1.4 动力学模型
1.4.1 干燥动力学模型 选取8种常用的干燥模型[13]来对烘烤过程中烟叶水分比与时间的变化进行拟合,8种干燥动力学模型的数学表达式如表1所示。
1.4.2 收缩动力学模型 选取3种体积收缩模型[9]来拟合烘烤过程中烟叶体积比随时间的变化,3种收缩动力学模型的数学表达式如表2所示。
1.4.3 数学模型拟合度评价 将试验结果代入上述模型进行计算,根据拟合结果的确定系数R2和均方根误差(root mean square error,简称RMSE)来对数学模型拟合度进行评估,其中R2越接近于1,RMSE越低,说明模型拟合度越高。
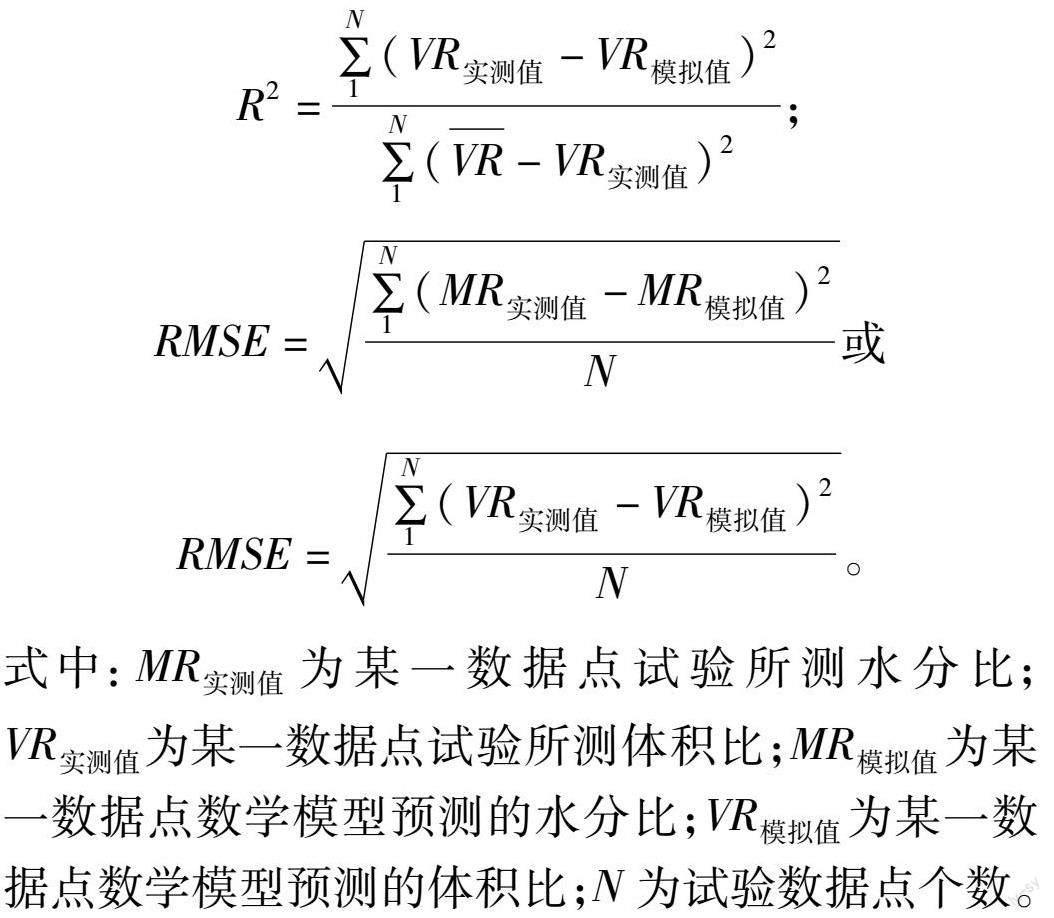
式中:MR实测值为某一数据点试验所测水分比;VR实测值为某一数据点试验所测体积比;MR模拟值为某一数据点数学模型预测的水分比;VR模拟值为某一数据点数学模型预测的体积比;N为试验数据点个数。
2 结果与分析
2.1 干燥特性分析
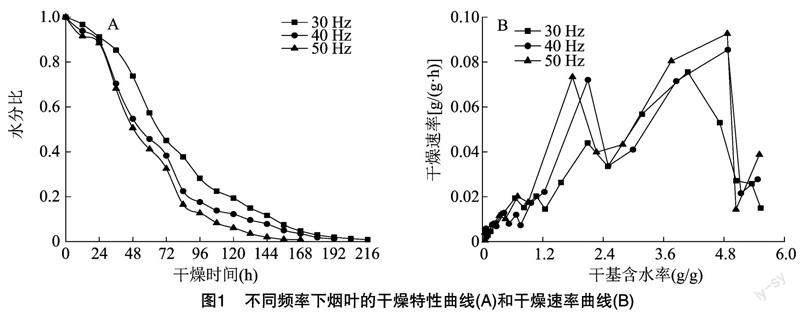
2.1.1 频率对烟叶干燥特性的影响 不同风机频率下烟叶的干燥特性和干燥速率曲线如图1所示。由图1-A可知,烟叶的水分比随干燥过程的进行逐步降低,烟叶达到完全干燥的时间随风机频率的增大而减少,这是由于风机频率的增大促进了烟叶、烤房内环境、外界环境三者之间的湿热交换,加快了烟叶內部水分从内向外迁移,使其烘烤时间大大缩短。在风机频率分别为30、40、50 Hz时,烟叶达到或低于目标含水率6%的时间为216、192、168 h。24 h以前,不同频率下烟叶的水分比相差不大,这可能是由于试验所采用的烘烤工艺为变黄前期保湿变黄所导致。由图1-B可知,随着风机频率的增大,同一干基含水率下烟叶的干燥速率相应较大。40 Hz和50 Hz下烟叶干燥速率在干基含水率4.8~5.4 g/g之间达到极大值,30 Hz下烟叶干燥速率在干基含水率3.6~4.2 g/g之间达到极大值,这与李生栋等的研究结果相一致,可能是烘烤前期叶表面附着水被干燥及烟叶内水蒸气分压迅速与外界环境达到平衡所导致[5]。各频率下烟叶的干燥速率在干基含水率1.2~2.4 g/g之间呈先上升后回落的趋势。可能是由于烟叶在变黄后期转入定色期时进行了升温和加大排湿操作(48~72 h),叶表面内外水汽平衡状态被打破,加大了干燥速率。在烘烤中后期,干基含水率为0.0~1.2 g/g 之间时,同一干基含水率下各频率的干燥速率差距在逐渐缩小,这可能是由于烟叶经预热完成后,烟叶内部与外界的水分梯度减小,水分迁移速率降低。
2.1.2 不同频率下烟叶的干燥动力学模型 风机频率不同时,烟叶对应的干燥数学模型也有区别,为准确筛选出最适宜描述变频处理下烟叶干燥状态的数学模型,在保持装烟室内烟叶成熟度基本相同的前提下,采用常见的8种干燥数学模型对30、40、50 Hz下烟叶水分比变化进行拟合。根据拟合方程的R2和RMSE来衡量模型对烟叶干燥变频调控手段的吻合程度。30、40、50 Hz的MR-t拟合曲线分别见图2-A、图2-B、图2-C,其拟合结果如表1所示。
由表3对比8种常见的干燥数学模型所得R2和RMSE值发现,多种数学模型的R2均达0.990水平,说明频率调控烟叶干燥中的水分散失动力学可用多种模型描述。其中风机频率30 Hz时以Modified Page、Page、Wang et al. 和Diffusion approach模型的R2均为0.997,RMSE值为0.021,拟合程度较好;风机频率40 Hz时,Modified Page、Page和Wang et al. 模型的R2取最大值0.995,RMSE最小值均为0.027,拟合程度最好;风机频率50 Hz时,Modified Page和Page模型的R2值为0.996,RMSE值为0.024,拟合程度最好。Logarithmic模型在3个频率处理下的R2值均低于0.3,RMSE值都大于0.3,这表明Logarithmic模型对通过频率调控烟叶干燥的拟合程度较差。综合不同频率下的干燥模型拟合结果来看,Page和Modified Page模型用来描述烟叶烘烤中不同频率条件对烟叶水分变化的影响最为适宜。
2.2 收缩特性分析
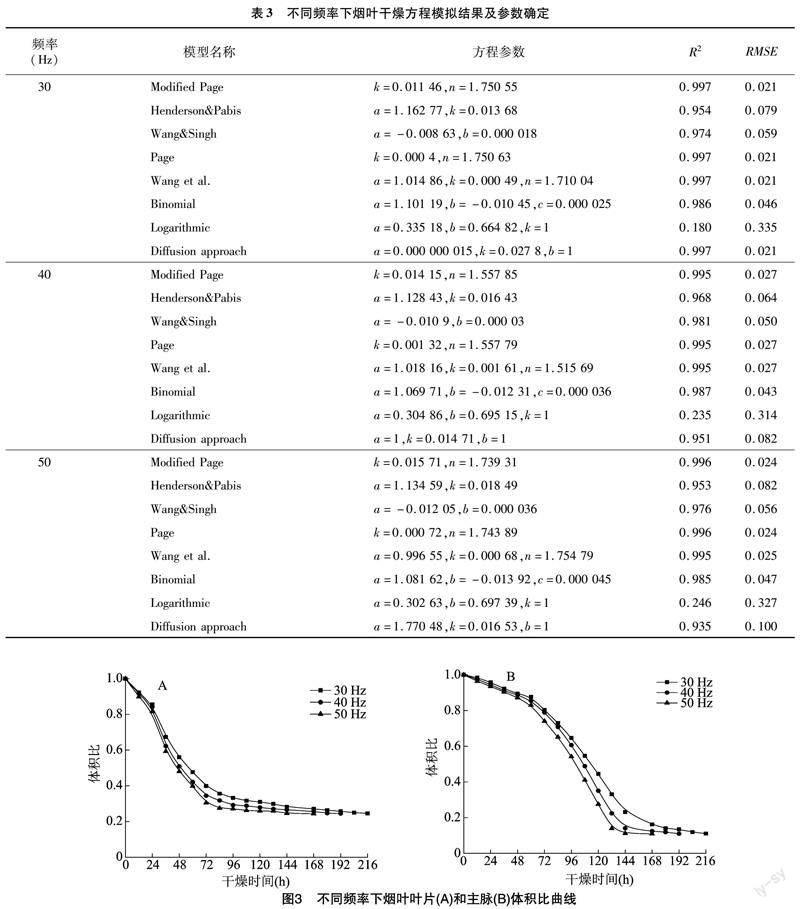
2.2.1 频率对烟叶收缩特性的影响 由图3可知,随着烟叶烘烤过程的进行,烟叶的体积逐渐缩小至其完全干燥时的体积。此外,在整个烘烤过程中,烟叶叶片和主脉的收缩变化并不相同。其中,烘烤前期(0~72 h),叶片的收缩速率较快,收缩程度较高,而主脉的收率速率较慢,收缩程度不大。烘烤中期(72~120 h),叶片收缩趋势变缓,主脉加速收缩。烘烤后期(120 h至烘烤结束),叶片和主脉都进入降速收缩阶段。从烘烤结束时的体积比来看,与鲜烟叶相比,烟叶经烘烤后叶片收缩至20%左右,主脉收缩至10%左右。这是由于从变黄后期转入定色期,叶片内大量水分迅速排出,收缩速率明显加快。烘烤中期时虽然温湿度梯度进一步加大,但由于叶片内水分含量降低,而此时主脉含水量较高,主脉内水分迁移至叶片后经热空气排出,使叶片收缩速率下降的同时也加快了主脉的收缩。烘烤后期时,叶片接近全干,水分迁移通道被破坏,主脉内水分散失速率下降,导致叶片和主脉的收缩速率都减小直至干燥完成。由图3还可以看出,烟叶叶片和主脉的收缩速率与风机频率的大小具有明显正相关性,风机频率的增大可以加速烟叶的收缩率,这与不同频率下烟叶的干燥特性相符合。
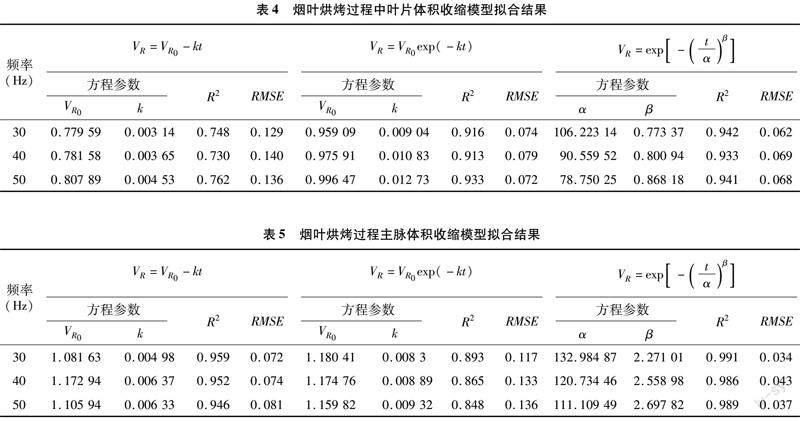
2.2.2 烟叶的收缩动力学模型 3种不同分布函数下烟叶烘烤过程中的收缩动力学模型如表4、表5所示。其中,R2越接近于1,RMSE越接近于0,代表模型的拟合结果精度越高。对叶片收缩的拟合中,0阶模型的R2在0.730~0.762之间,RMSE在 0.129~0.140之间;一阶模型的R2在0.913~0.933之间,RMSE在0.072~0.079之间;Weibull分布函数的R2在0.933~0.942之间,RMSE在0.062~0.069之间。对主脉收缩的拟合中,0阶模型的R2在0.946~0.959之间,RMSE在0.072~0.081之间;一阶模型的R2在0.848~0.893之间,RMSE在0.117~0.136之间;Weibull分布函数的R2在0.986~0.991之间,RMSE在0.034~0.043之间;Weibull分布函数最能描述烟叶烘烤过程中叶片和主脉的收缩变化。其中,Weibull分布函数中的尺度参数α为干燥过程中的速率常数,其数值大约为干燥完成时间的63%。在对烟叶的烘烤中,风机频率由30 Hz提升至50 Hz时,Weibull分布函数叶片收缩模型中的α值从106.2减小至78.8,主脉收缩模型中的α值从133.0减小至111.1。上述结果表明,增大风机频率会导致对应的α值降低,明显缩短烘烤时间。
2.3 有效水分扩散系数
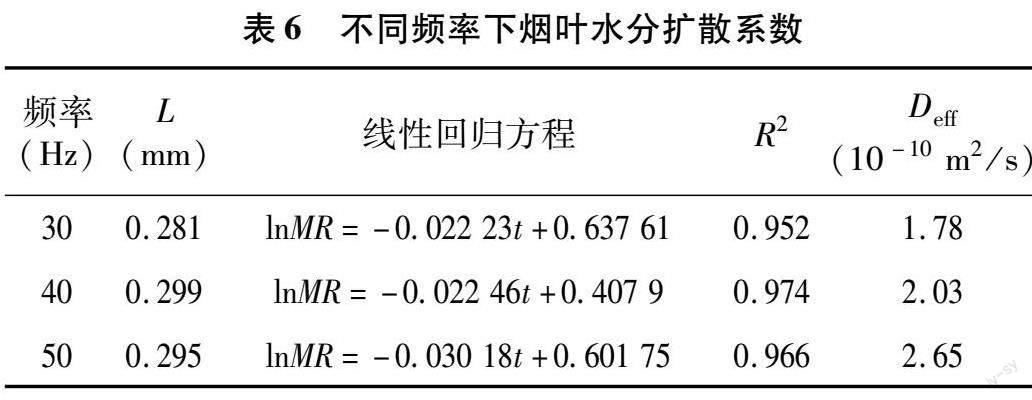
有效水分扩散系数表示烘烤过程中烟叶的脱水能力,是反映烟叶内水分扩散情况的重要指标。利用Origin 2021分别绘制不同频率下烟叶烘烤过程中的ln(MR)与t的关系图,并用一元线性方程对曲线进行拟合,从而得出不同风机频率下烟叶的ln(MR) 与t的线性回归方程。烟叶的有效水分扩散系数根据公式(4)、(5)计算得到,如表6所示。可以看出,当风机频率由30 Hz增至50 Hz时,烘烤过程中烟叶的有效水分扩散系数从1.78×10-10 m2/s 增至2.65×10-10 m2/s,这是由于风机频率的增大加速了水分子的汽化,促进了水分的扩散和迁移,使有效水分扩散系数增大;这表明适当增大风机频率可以有效增加烟叶烘烤过程中的有效水分扩散系数。
2.4 数学模型验证
为验证已得数学模型公式的准确性,随机选取一组试验条件,对其实测值与模型预测值进行比较。拟合曲线如图4所示,其中图4-a为 40 Hz下烘烤过程中Modified Page模型的拟合结果,图4-b为40 Hz下烘烤过程中Page模型的拟合结果,可以发现试验中水分比实测值与对应模型预测值基本在1 ∶ 1线上,说明Modified Page和Page模型都能较好地模拟不同频率下烟叶烘烤过程中的干燥状况。图4-c为40 Hz下烘烤过程中Weibull分布函数对叶片体积收缩的拟合效果,圖4-d为对应条件下主脉体积收缩的拟合曲线,可以看出,两者的线性拟合系数均接近于1,且r2>0.99,这表明Weibull分布函数可以很好地模拟不同频率下烟叶烘烤过程中的体积收缩状况。
3 讨论
烟叶烘烤的本质是变黄与干燥的统一[14],装烟量和烘烤工艺固定时,烟叶的失水速率与风机频率息息相关[15]。刘闯研究表明,定色期风机转速 960 r/min 时,烤房排湿速率低于烟叶水分散失速率,烟叶失水受限,而风机转速1 450 r/min时,烟叶失水速率明显增大[16]。这与本研究中相同时间节点下,高风机频率烟叶水分比较小具有一致性。另有研究显示,与常规风机频率相比,高风机频率处理可以明显缩短烘烤时间19 h[17]。这与本研究中全程50 Hz时烟叶最先达到完全干燥具有一致性,但在具体烘烤缩短时效上,两者有所差异,可能是由于变频处理的具体设置和装烟量不相同所导致。Weibull分布函数中尺寸参数值α的变化也验证了这一趋势,风机频率30~50 Hz时,对应的叶片α值为106.2~78.8,主脉α值为133.0~111.1,说明烘烤过程中主脉干燥所需的时间远大于叶片,这在李铮等的研究[18]中得到了证实,是由于烘烤前中期主脉水分不断迁移至叶片所导致。
本研究显示不同频率烘烤时烟叶的干燥特性和收缩特性趋势相同,风机频率的增大会加速烟叶的干燥和收缩。当风机频率由30 Hz增至50 Hz时,烟叶有效水分扩散系数由1.78×10-10 m2/s增至2.65×10-10 m2/s也证实了这一现象,表明高风机频率可以促进烟叶水分内部迁移和外部扩散从而加速烟叶的干燥和收缩。但在具体收缩趋势上,144 h 前叶片体积的收缩呈降速趋势,主脉体积的收缩呈增速趋势,这是由于45~48 ℃之间,叶片失水占比减小,主脉失水增大[19]。
李生栋等曾提出Wang and Singh模型可以作为云南87不同部位烟叶干燥动力学模型[5],与本研究结果有所出入。这可能是由于在试验时采用的烟叶品种、烘烤工艺、风机频率和装烟量不相同,使烟叶的干燥曲线出现一定差异。建立风机频率对烟叶烘烤过程中干燥和收缩的动力学模型也会因烟叶品种、成熟度和地区差异而受到影响。因此,后续研究将逐渐加入品种特性和鲜烟素质等控制因素,构建出完善的烟叶变频烘烤动力学模型。
4 结论
Page和Modified Page模型可以很好地描述不同频率烘烤时烟叶的水分变化,Weibull分布函数可以很好地预测不同频率烘烤时烟叶的收缩状况,综合烟叶的失水和收缩情况,两者可以为烘烤过程中确定适宜的风机频率参数提供科学的理论依据。
参考文献:
[1]李昱霖,刘明宏,刘家旺,等. 响应面法优化烟叶变频烘烤工艺[J]. 中国烟草学报,2021,27(1):83-89.
[2]刘光辉. 密集烘烤风机变频调速对烘烤工艺和烟叶质量的影响[D]. 长沙:湖南农业大学,2010:19.
[3]刘 闯,王学龙,豆显武,等. 变频调速技术在烟叶密集烘烤中的应用研究初报[J]. 浙江农业科学,2010,51(3):563-566.
[4]谭林彬. 烤烟密集烤房适宜风机研究[J]. 湖南农业科学,2011(18):38-39.
[5]李生栋,付宗仁,胡蓉花,等. 烟叶烘烤过程中水分变化及干燥数学模型构建[J]. 南方农业学报,2018,49(1):121-129.
[6]魏 硕,徐 宸,王松峰,等. 预凋萎烟叶烘烤过程中水分迁移干燥及形态收缩特性[J]. 西北农林科技大学学报(自然科学版),2018,46(6):39-47.
[7]李昱霖,丁应福,王胜雷,等. 烤烟烘烤过程风机频率对叶温和烟叶变黄失水的影响[J]. 河南农业科学,2022,51(3):173-180.
[8]宫长荣. 烟草调制学[M]. 2版. 北京:中国农业出版社,2011.
[9]刘 鹤,焦俊华,田 友,等. 马铃薯片热风干燥特性及收缩动力学模型[J]. 食品工业科技,2022,43(11):58-64.
[10]黄光群,余 浩,方 晨,等. 奶牛粪固形物热风干燥特性及工艺参数优化[J]. 农业工程学报,2021,37(23):186-193.
[11]梁 淼,侯 佩,芦昶彤,等. 金钱草多糖对片烟干燥动力学特性的影响[J]. 云南农业大学学报(自然科学),2019,34(1):70-77.
[12]宋 玉,刘 超,段依梦,等. 稻谷就仓干燥水分迁移规律及干燥动力学模型研究[J]. 中国糧油学报,2021,36(10):115-123.
[13]吴小华,马渊博,宁旭丹,等. 西洋参分段式热风干燥动力学模型构建[J]. 农业工程学报,2020,36(5):318-324.
[14]仙立国,王松峰,孙帅帅,等. 热泵密集烤房对烟叶烘烤主要生理变化和质量的影响[J]. 中国烟草科学,2021,42(6):53-59.
[15]李旭华,邱妙文,文 俊,等. 变频电机对密集烘烤烟叶质量的影响[J]. 中国烟草科学,2012,33(1):74-77.
[16]刘 闯. 变频调速对密集烤房流场及烟叶烘烤质量的影响[D]. 郑州:河南农业大学,2011:20.
[17]许 齐,刘杨舟,罗会斌,等. 不同变频风速对烤烟烘烤成本及经济效益的影响[J]. 贵州农业科学,2012,40(9):90-92.
[18]李 峥. 烘烤中基于色度学的烟叶颜色变化与水分及化学成分关系[D]. 郑州:河南农业大学,2019:19-21.
[19]夏 春,范宁波,王 彬,等. 成熟度对云烟87上部烟叶烘烤中失水特性的影响[J]. 福建农林大学学报(自然科学版),2020,49(2):159-166.

