基于双层协调体系的多圆碟形AUG路径规划

王浩亮,孙定翔,马小轩,王丹,吴浩峻

(1.大连海事大学 轮机工程学院,辽宁 大连 116026;2.大连海事大学 船舶电气工程学院,辽宁 大连 116026)

21世纪是海洋的世纪,我国是拥有300万平方公里主张管辖海域、1.8万公里大陆海岸线的海洋大国,关心海洋、认识海洋、经略海洋,加强海洋观测与探测,事关国家战略安全与长远发展。水下自主滑翔机(autonomous underwater gliders,AUG)作为一种新型的水下自主航行器(autonomous underwater vehicle,AUV),在军事和民用领域有着广泛的应用,是预警探测、反潜侦察、海洋观测、资源探测、搜救打捞的重要工具[1-3]。路径规划技术是智能水下机器人的关键技术之一,是指为了到达某个目标或完成某个任务,对所规划设备的航行方向、航行路线等进行预先计算、设定、优化的过程[4]。

学界对单体路径规划问题已经研究了数十年,文献[5]通过采用基于量子行为的粒子群优化算法解决了以能耗优化为目标的水下滑翔机在洋流环境下的路径规划问题,文献[6]提出了一种角制导快速行进方阵规划算法能够根据航行器的运动约束计算最优路径,文献[7]基于生物启发神经网络解决了三维海洋环境下的实时避障问题,文献[8]考虑了变海流情况下的最短时间航行的路径规划问题。

在单体的路径规划方面目前已有较多成果,而针对多智能体的路径规划研究较少。文献[9]考虑了一种多AUV集群在不同起始位置同时到达同一目标位置的情况,文献[10]通过SOM神经网络对每个AUV进行任务分配,并通过速度综合法规划每个AUV访问相应区域的最短路径,文献[11]提出了一种基于分布式壳空间分解的多自主航行器交会航迹规划方法。该方法结合优化的质心交汇点选择方案和基于B-Spline的量子粒子群优化技术,寻找多航行器的最优交会轨迹。以上多AUV路径规划方法虽然可对多AUV规划出满足要求的路径,但是并未考虑AUV之间的避碰问题。

AUG在进行海洋观测时,作业航程可达数千公里,续航时间可达数月[12-13],远高于其他自治式水下航行器[13],由于AUG携带锂电池容量有限,因此以低能耗为重要技术指标的AUG对能量使用有着更高的要求,即便如此,在导致圆碟形AUG观测任务失败的原因中能源问题仍高居第二位[14]。另外,当电量不足时,AUG需通过母船补给或者提前返航获得能量,能源补给较为困难,因此需要尽可能在能耗最低的情况下实现圆碟形AUG集群的路径规划。

鉴于此,本文研究了复杂海洋环境下以航行能耗最优为目标的多AUG路径规划问题。本文首先建立了AUG的航行能量消耗模型及海洋环境模型,然后在此基础上提出一种基于全局与局部双层协调的多AUG路径规划体系,最后结合最小一致偏差法(biased min-consensus,BMC)和人工势场法,为每艘AUG规划出既能满足能耗最优又能满足避障避碰要求的三维安全路径。

1 圆碟形水下滑翔机建模方法

圆碟形AUG的能量消耗与其自身设计、海流速度、航行距离和航行速度等多种因素相关。当以能量消耗作为AUG路径规划的优化目标时,一个合适的能耗模型就显得至关重要。总体而言,基于能耗最优的路径规划即为在从起点到目标点的众多可行路径中求解出一条能耗最小的路径。航行路径是由从起点PS至目标点PD之间的一系列离散路径点Pxy={PS,P1,P2,…,PM,PD}连接而成的折线。平面中每一个路径点都有一个速度矢量,用来表示该区域内的海流速度Vc。AUG的稳态滑翔速度与净浮力和滑翔角有关,由于在AUG稳态运动过程中,其净浮力和滑翔角基本保持不变,为了提升运算速度且简化能耗模型,可将对水航速V设为定值。

AUG的运动轨迹类似锯齿形,整个航程可分为若干个周期,其中每个周期的轨迹如图1所示,θ、α和Θ分别为俯仰角、攻角和航迹角。根据AUG的能量消耗方式,在单个定常运动周期内的总能耗可分为2部分：1)与滑翔周期有关,如姿态调节系统、浮力调节系统和通信定位系统产生的能耗;2)与滑翔时间有关,如测量传感器和嵌入式控制系统产生的能耗。

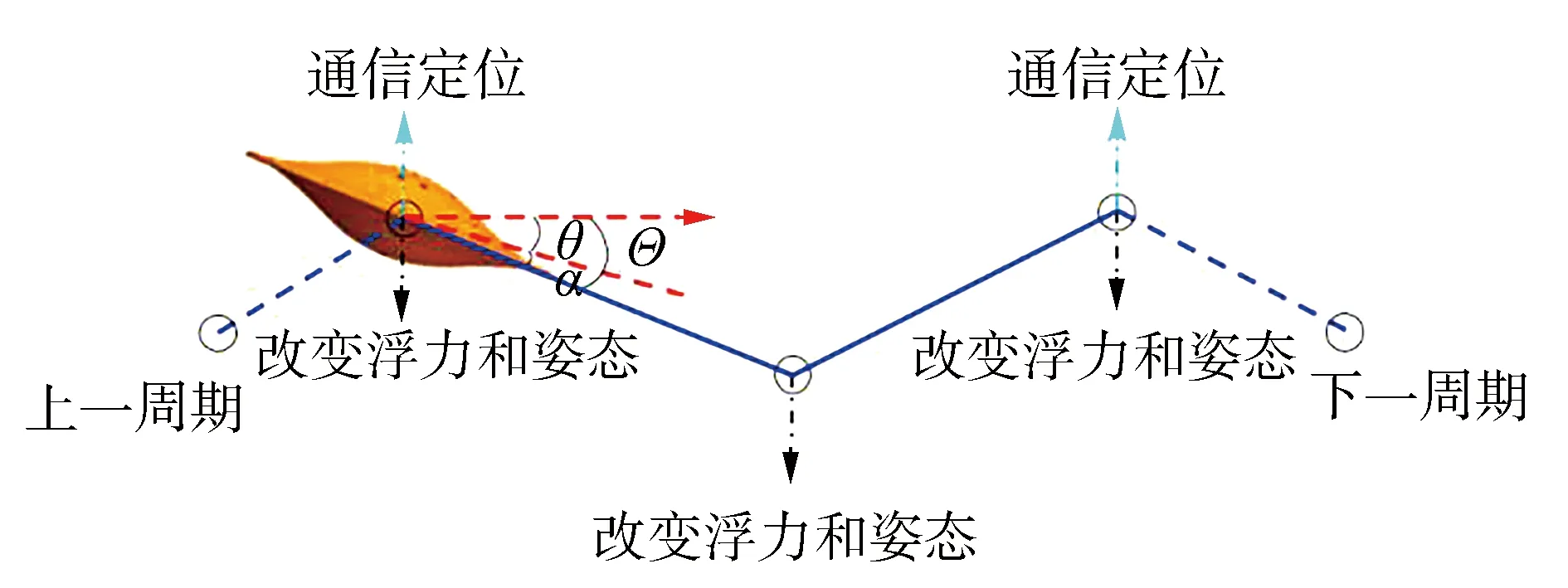
图1 AUG滑翔周期示意Fig.1 Schematic diagram of AUG gliding cycle

1.1 与滑翔周期有关的能耗

与滑翔周期有关的能耗主要包括浮力调节系统产生的能耗、姿态调节系统产生的能耗和通信定位系统产生的能耗3部分。

1)浮力调节系统产生的能耗：圆碟形AUG浮力调节系统主要分为下潜时油箱压力变为负压从外油囊吸油和上浮时油箱压力变为正压向外油囊排油2个流程,为防止油箱和外油囊因压力差而发生内漏,液压油泵配有单向阀。浮力调节系统原理图如图2所示。

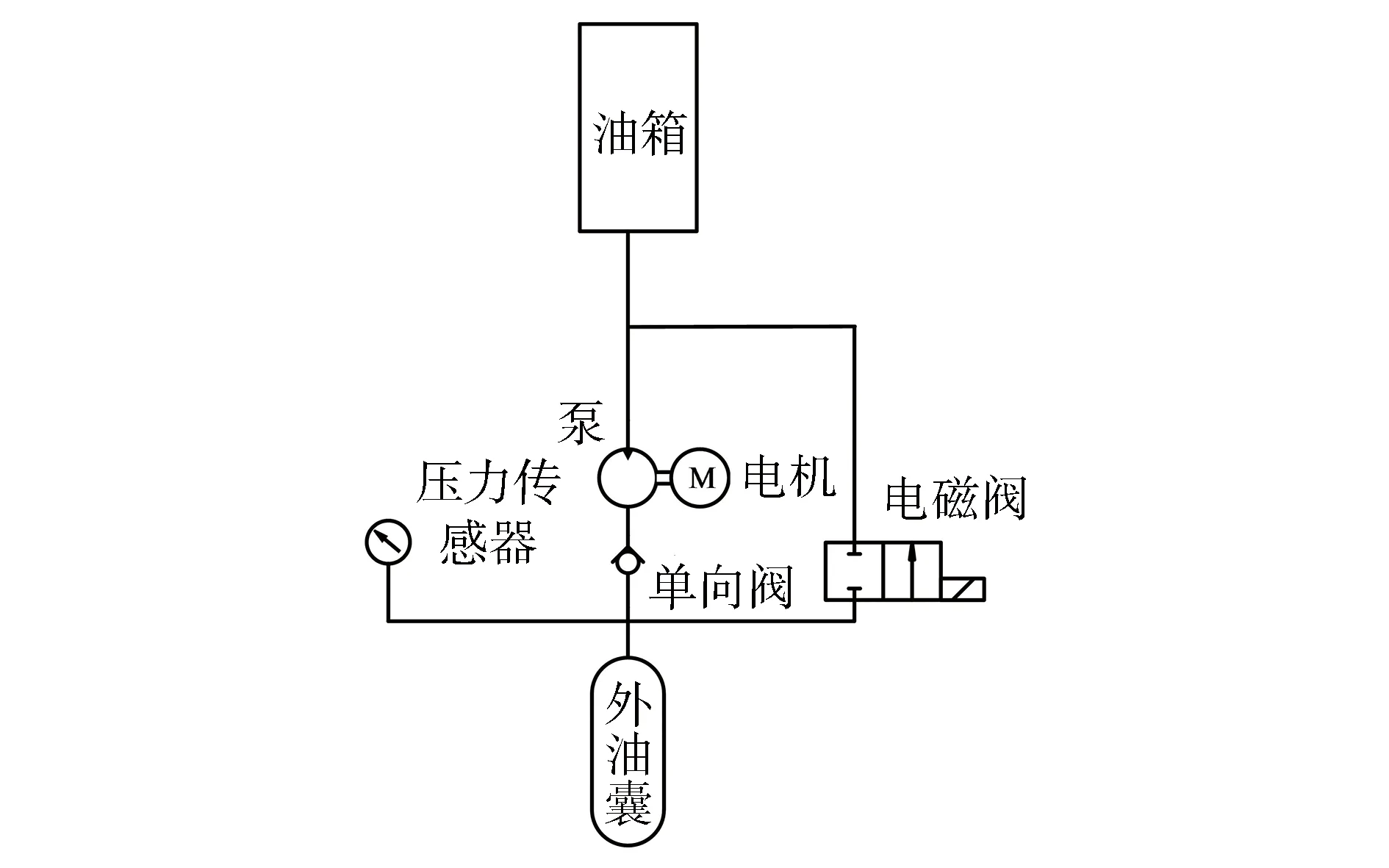
图2 浮力调节系统原理Fig.2 Schematic diagram of buoyancy regulation system

AUG在海面需要下潜时,根据指令要求,电磁阀开启,同时气泵将油箱内的气体抽到油箱外,使外油囊内的液压油在外部水压和油箱负压的驱动下抽吸到油箱。此时,外油囊体积减小使AUG的浮力小于重力,执行下潜动作。在下潜抽油的同时,通过传感器测量进入油箱的液压油体积,满足油量要求后关闭电磁阀。

由上述工作过程可知：下潜抽油阶段能耗Efd主要与电磁阀和气泵有关,将气体看做不可压缩的理想气体,则Efd可表示为：

(1)

式中：Bd为下潜净浮力;Pv和Pa分别为电磁阀功率和气泵功率;qv和qa分别为液压阀流量和气泵流量;ρ为海水密度;g为重力加速度。

AUG在水下需要上浮时,浮力调节系统收到指令后,起动电机驱动液压泵将液压油从油箱排至外油囊。此时,外油囊体积变大,使AUG的浮力大于重力,执行上浮动作,充入的油量满足要求时停泵。在充油的同时,气泵工作,使油箱始终处于正压状态,避免液压泵吸空。

液压泵的输入功率Pp为：

(2)

式中：qp为液压泵排量;ηP为液压泵效率;H为下潜深度。由此可得液压泵拖动系统消耗的功率Ph为：

(3)

式中：Pm0、Ue、I0和ηm分别为液压泵拖动电机的空载功率、额定电压、额定电流和效率;ηP为液压泵的效率。由上述工作过程可知上浮排油阶段能耗Efu可表示为：

(4)

式中Bu为上浮净浮力。

由此可得,单个滑翔周期中浮力调节系统产生的能耗Ef为：

(5)

2)姿态调节系统产生的能耗：AUG在上浮与下潜2种状态之间转换时,需要通过电机移动滑块来改变机身重心,由此产生能量消耗。由于AUG主要在纵剖面做定常滑翔运动,所以这里主要考虑俯仰姿态调节产生的能耗。假设静水环境下,AUG在调节过程中浮心位置不变,忽略攻角影响,根据力矩平衡可得从水面开始下潜时,滑块偏离平衡位置的位移xp1为：

(6)

式中：m为AUG质量;h0为AUG的稳心高度;mp1为滑块质量。

由于圆碟形AUG机身轴对称,假设下潜和上浮过程的滑翔角相同,那么在单个滑翔周期下,滑块的位移可分为3部分：在海面由水平转至下潜状态时,滑块位移为xp1;由下潜转至上浮状态时,滑块位移为2xp1;由上浮转至海面水平状态时,滑块位移为xp1。由1.1节分析可知,纵向滑块由2台电机驱动,因此上浮或下潜姿态调节系统产生的能耗EZ为：

(7)

式中：Pm为滑块拖动电机功率;vp1为滑块移动速度。

3)通信定位系统产生的能耗：AUG的通信定位系统只有在浮出水面后才开始工作,属于间断工作制元器件。由于AUG在水面进行通信定位的时间及漂浮距离与水下相比很小,可忽略不计,假设每个滑翔周期都进行通信定位,则在单个滑翔周期产生的能耗Ec为：

Ec=Pctc

(8)

式中Pc和tc分别为通信功率和通信时间。

1.2 与滑翔时间有关的能耗

与滑翔时间有关的能耗主要来自测量传感器和嵌入式控制系统等,圆碟形AUG的嵌入式控制系统通常处于运行状态,其功率依赖于控制软件[15]。假设嵌入式控制系统的平均功率在一个滑翔周期内为常数,则单个滑翔周期的滑行时间为：

(9)

嵌入式控制系统的能耗模型可定义为：

(10)

式中Pc是嵌入式控制系统的平均功率,可以通过实验预先测量。

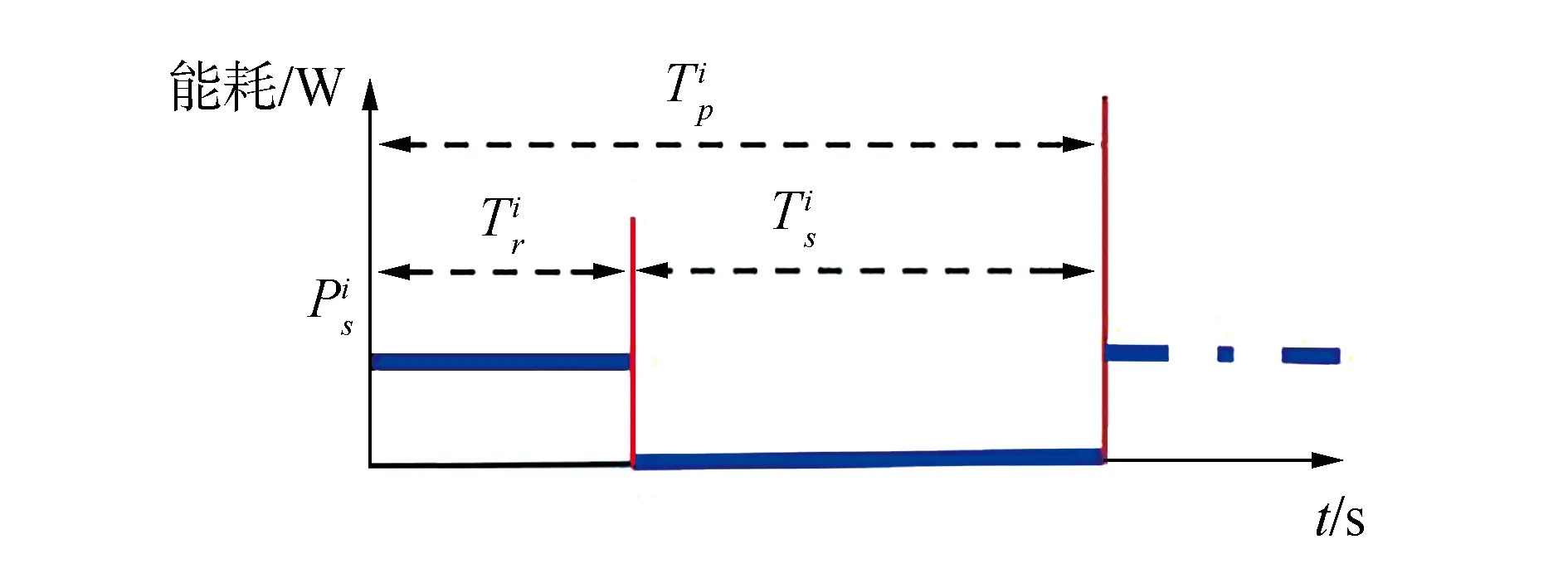
图3 机载传感器的间歇性操作Fig.3 Intermittent operation of sensors onboard AUG

(11)

(12)

第i个传感器的能量消耗可表示为：

(13)

将式(9)、(11)和(12)代入式(13),得到第i个传感器的能耗模型为：

(14)

因此,所有传感器的能耗可表示为：

(15)

综上所述,第i个圆碟形AUG在一个滑翔周期内的总能量消耗为：

E=Efd+Efu+2Ez+Ec+Em+Es=

(16)

2 双层协调体系构建

在目前的多海洋航行器路径规划方法中,采用全局规划算法很难应对局部路径的实时协调,而倾向于局部规划的方法又难以形成优质的全局路径。针对这一问题,本文提出一种基于全局与局部双层协调的多AUG路径规划体系,结合BMC算法和人工势场法,通过全局与局部路径的相互协调,保证AUG在沿全局最优路径行驶时,仍能够灵活调整局部路径,从而进一步提高多AUG系统的全局规划与局部协调能力,体系结构图如图4所示。

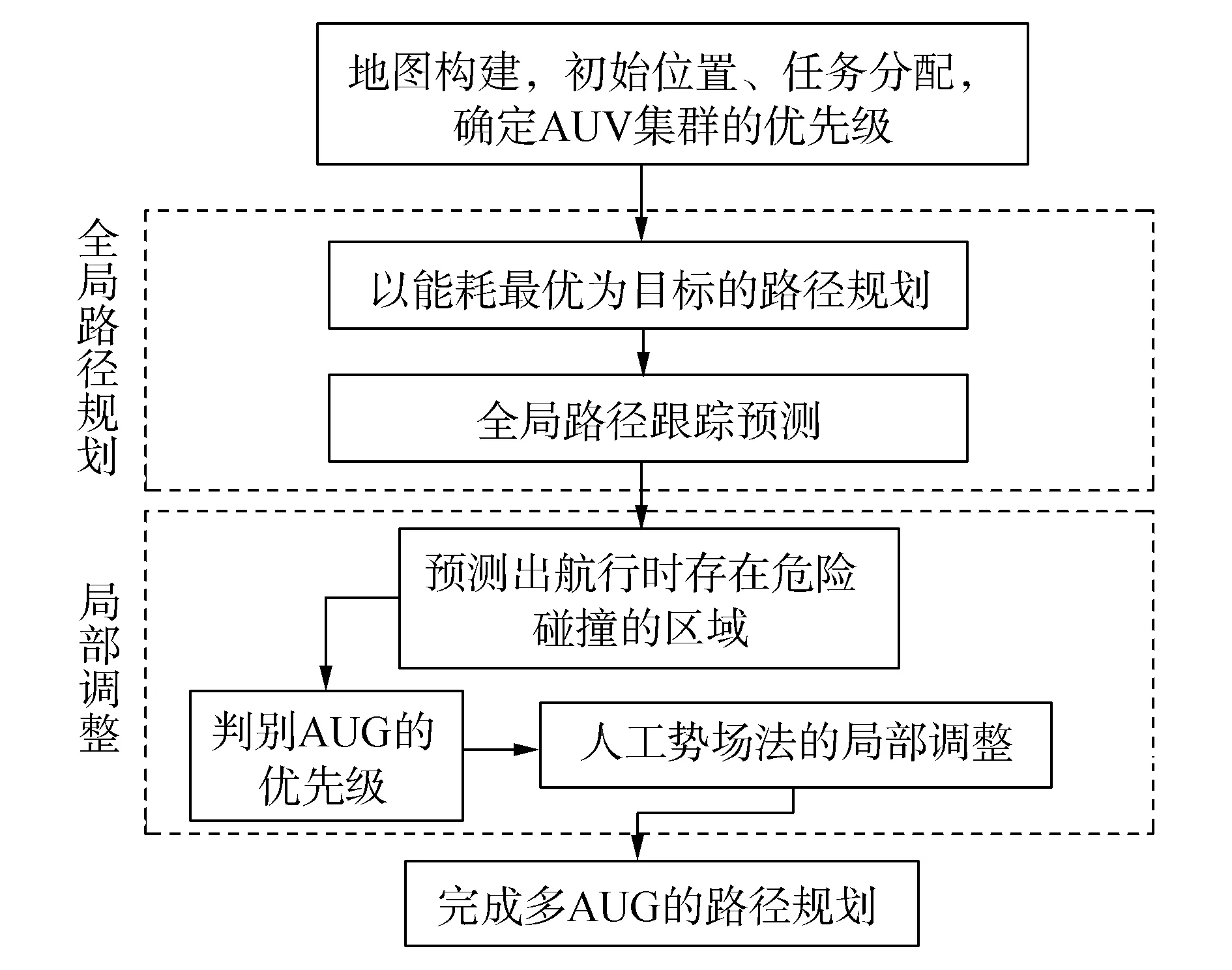
图4 体系结构Fig.4 Architecture diagram

在路径规划时,首先对洋流、岛屿等环境信息进行环境地图的构建,同时确定各AUG的初始位置和目标位置,并根据各AUG所需完成的任务的重要程度或者其他因素来决定AUG的优先级顺序。经过规划全局路径规划可实现AUG与障碍物的无碰撞以及各AUG到达目标点的能耗最优,但无法处理多AUG彼此之间的航行干扰,即无法保证足够的航行安全距离,因此仅依靠单次的全局路径规划无法满足多AUG能耗最优的路径规划要求,所以需要对全局路径进行局部的调整,调整的方法主要考虑为动态地避开危险碰撞区域。计算危险碰撞区域的方法如下。

经过全局路径规划可以获得每艘AUG从起始点到目标点的优化路径,根据相应路径可以计算出AUG经过各路径点的时刻,并以此来预测出AUG间可能存在碰撞的路径点。

如图5所示,(Pim,Pim+1)和(Pjn,Pjn+1)分别第i艘和第j艘AUG全局路径中的2个路径点,第i艘的优先级低于第j艘,Pimm+1和Pjnn+1分别为对应的2条路径,当2条路径相交时2艘AUG存在碰撞危险,此时应分别计算2艘AUG到达路径交叉点处的时间消耗ti和tj,同时为了达到足够的安全性考虑了安全时间t0和安全距离rs,则在[ti-t0,ti+t0]时间内的危险区域如图中阴影区SjAUG所示,当优先级较低的第i艘AUG出现在SjAUG区域时,即认为避碰危险发生。通过让优先级低的AUG调整航线来避让优先级高的AUG所产生的避碰危险区域,以此来防止碰撞的发生。

图5 AUG避碰危险发生示意Fig.5 Schematic diagram of danger occurrence of AUG collision avoidance

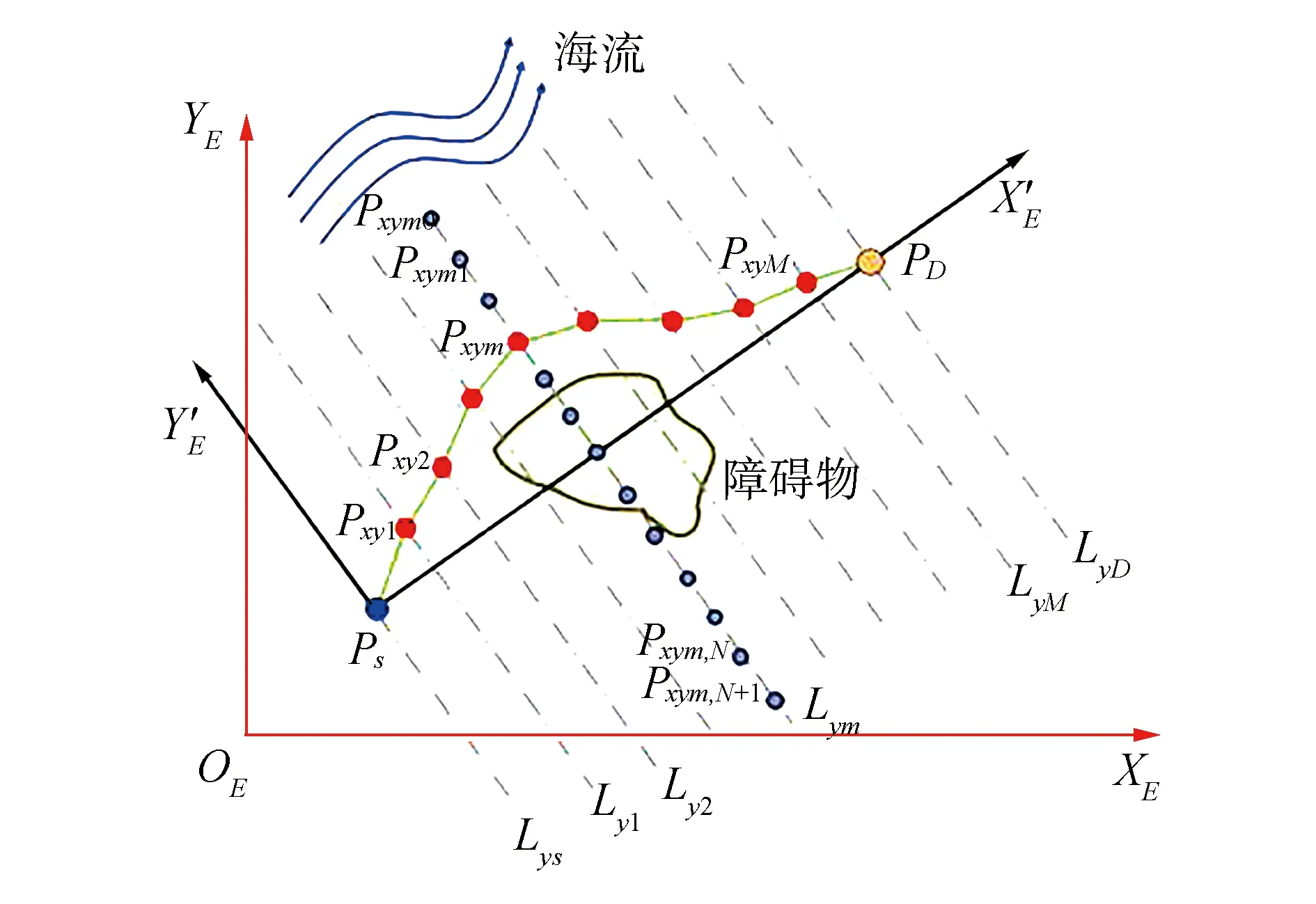
图6 水平面离散建模示意Fig.6 Horizontal plane discrete modeling diagram

3 基于BMC算法的全局路径规划

3.1 BMC算法回顾

令G={V,ε}为一个加权的无向连通图,其中V={1,2,…,Nv}为节点集,每个路径点对应一个节点。ε={(ii,j)∈V×V}为任意2个节点的无序对集合,称为边集。令lij=(i,j)为连接节点i和节点j的边,xi为节点i的状态值,wij为边lij的权值且始终为正。由此可得,以搜索目标函数最小值为例,基于图论的路径规划问题可表示为：在图G={V,ε}中找到一条从节点S∈V到节点D∈V的路径,并使组成该路径的边所对应的权值之和最小。

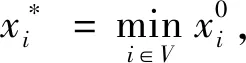
(17)

(18)

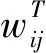
(19)

3.2 考虑能耗最优的BMC算法

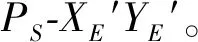
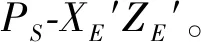
图7 纵平面离散建模示意Fig.7 Diagram of vertical plane discrete modeling

上述采用路径解耦方法规划出的水平面最优路径点集合Pxy={PS,Pxy1,Pxy2,…,PxyM,PD}和纵平面最优路径点集合Pxz={PS,Pxz1,Pxz2,…,PxzM,PD},每一维度上的路径点在XE′轴上具有相同的坐标,因此可以将Pxy和Pxz中的路径点按照XE′轴上坐标一致的原则合成三维最优路径点集合Pxyz={PS,P1,P2,…,PM,PD},由此建立三维离散空间模型,将集合Pxyz中各节点依次相连形成的路径即为三维空间的最优路径。

在所有节点中,只有起始节点PS会被视为引导节点V1,其状态x1=0;其他节点均视为跟随节点V2。跟随节点的状态被定义为从起始节点到该跟随节点的能量消耗,其值可通过起始节点至计算该节点的沿途所有节点之间的边所对应的权值(2点之间的能量消耗)之和获得。

BMC算法本身属于启发式算法[9],可通过优化离散分布的路径点来实现对航行距离、航行时间等连续变量的优化。由能量消耗模型可知,AUG的能耗可分为与滑翔周期有关的能耗和与滑翔时间有关的能耗。与滑翔周期有关的能耗仅在AUG上浮到最高点或下潜到最低点附近的较短时间内产生,而在滑翔周期的其他时间段内没有这种能量消耗,并且滑翔周期数不一定为整数,因此在计算能量消耗时还需要考虑滑翔周期数的影响。传统的BMC算法在计算节点的状态值时仅考虑相邻节点的状态值和与相邻节点所连接边的权值,而对于AUG的能耗计算而言,还需要考虑经过某路径节点时所处的周期,以此来计算每段路径上调节浮力、姿态和通信定位的次数。如果一条边连接着2个路径节点Pi和Pj,则传送给节点Pi的信息不仅包括前一节点Pj的状态值、该边所对应的能量消耗,还增加了AUG已航行的周期数Cj=SSjtanΘ/(2H),SSj为节点Pj到起始节点PS的水平距离。通过计算从起始节点到该节点的周期数,可得出节点Pi与相邻节点Pj间调节浮力、姿态和通信定位的次数。

(20)

式中：Dijd表示节点Pi与相邻节点Pj间海面附近的浮力、姿态的调节次数和通信定位次数;Diju表示节点Pi与相邻节点Pj间最大工作水深附近的浮力和姿态调节次数;Ci和Cj分别为节点Pi和Pj处的已航行周期数;SSi和SSj分别为节点Pi和Pj到起始节点PS的水平距离。

定义节点Pi与相邻节点Pj间的连接权值为航行在该段路径上的能量消耗,考虑到节点不能出现在障碍物区域,加入了惩罚函数,则有：

(21)

式中：Xi为节点Pi的位置;SF表示障碍物所在区域。

尽管仅考虑障碍物范围外的节点可在一定程度上达到避障的效果,但是仍可能出现某节点与其相邻节点之间的边与障碍物区域重合的情形,为避免这种情况,继续使用惩罚函数,重新定义后的边的权值被表示为：

(22)

式中SF表示障碍物所在区域。

由此可知,离散空间模型中各节点的状态值为：

(23)

各节点的初始状态并不影响节点的稳定值,且最终的稳定值都等于当前节点至起始点的最低能耗。

4 基于人工势场法的局部调整

圆碟形AUG由于机翼与机身紧密融合形成类飞碟的流线型,不仅具备传统AUG锯齿状垂直剖面滑翔和螺旋滑翔的能力,还具有全向运动、定点锚泊、坐底观测、零航速回转等方面的优势,能够有效满足定向类传感器的装备需求,更适合采用集群形式组成传感器阵列执行长时间、高精度的海洋观测任务。在此应用场景下,由于圆碟形AUG数量众多,彼此之间距离也相对较近,因此AUG之间存在发生碰撞的风险。考虑到集群路径规划与单航行器路径规划的不同,本文在基于能耗最优进行圆碟形AUG三维全局路径规划的基础上,又考虑了采用局部路径协调来规避AUG之间发生碰撞的风险。与传统人工势场法在碍航物处产生排斥势场、在目标点处产生吸引势场不同,本文所提人工势场法在其它AUG处产生排斥势场,同时从已规划的全局路径产生吸引势场,使得AUG在规避碍航物后可以最终返回到全局规划路径之上。

图8为第i艘AUG在进行避障的过程中所受斥力的示意图。Frep1为第i艘AUG和危险区域产生的斥力分量,使2艘AUG之间具有远离的趋势。为提高动态避碰的性能,需进一步考虑各AUG间的相对速度,Frep2为第i艘AUG与第j艘AUG之间的相对速度产生的速度斥力分量,其大小与相对速度大小成正比,方向垂直于2艘AUG的相对距离方向,亦即相对速度在垂直于相对距离方向上的分量的反方向。斥力势场可表示为：

图8 AUG所受斥力示意Fig.8 Schematic diagram of repulsive force on AUG

(24)

式中：ri和rj分别表示第i艘AUG和第j艘AUG的位置;ρ(ri,rj)为2艘AUG之间的相对距离;ρ0为斥力场的影响范围;krep1和krep2的斥力场强度系数,则第i艘AUG所受的合斥力为：

Frep=-∇Urep(ρ(ri,rj))

(25)

若局部调整区域存在碍航物,则处理方法与避开危险碰撞区域方法相同。

引力部分可驱使AUG恢复于期望航行状态,如图9,将全局路径上匀速运动的参考位置P0设定为目标点,并对AUG产生引力作用,引力的表达式为：

图9 AUG所受引力示意Fig.9 Schematic diagram of gravity on AUG

(26)

式中：r0为路径上的参考位置的坐标;katt为引力系数。斥力和引力的合力为：

Ftol=Frep+Fatt

(27)

通过斥力与引力的合成力可计算出下一位置点,直到合力将AUG拉回全局路径。在局部协调过程中,AUG的对水速度大小始终保持不变,合速度的方向则与合力方向保持一致,局部调整的起始位置和终止位置分别对应了全局路径上的2个位置点,航向角也与全局路径上的航向保持一致,进而保证了2条跟踪路线的平稳切换。

该部分通过仿真实例验证所提基于人工势场法的局部路径规划的有效性。根据地图范围及实际运行状态选择的势场函数参数为：krep1=10,krep2=10,katt=10,第1艘AUG的优先级高于第2艘。图7为不同时刻2艘圆碟形AUG航行的历史轨迹。

图10中,由于AUG1的优先级高于AUG2,根据局部调整的规则,AUG2需要进行避让。t=150 s为航行初始阶段,此时AUG2并未进入AUG1的斥力影响范围;t=250 s为AUG2进入AUG1的斥力范围,AUG2为保证避让而提前改变航向;t=400 s为AUG2通过调整航向成功避开AUG1,防止了危险的发生;t=750 s为AUG2经过局部调整后重新返回全局路径。

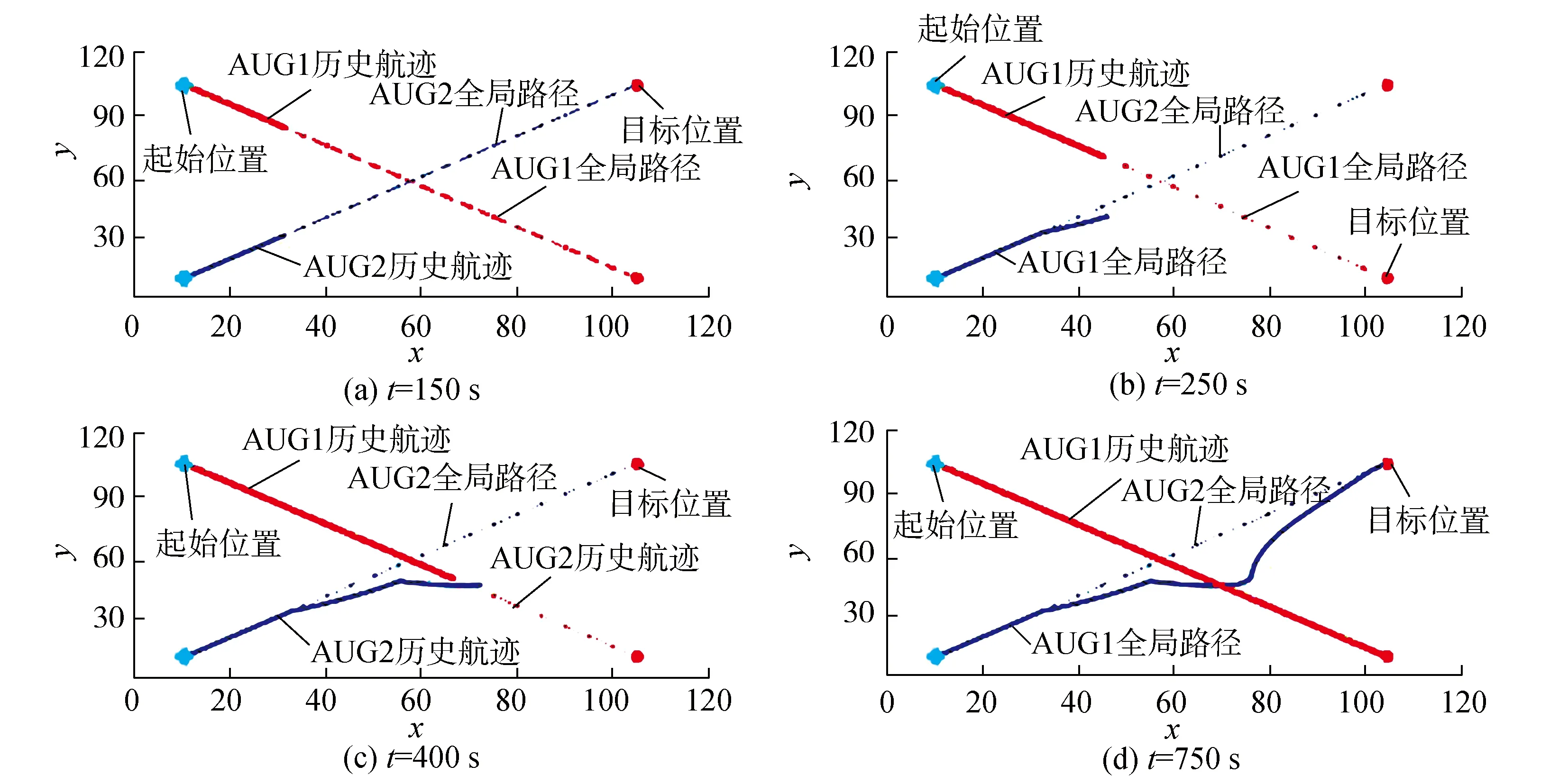
图10 AUG避碰图Fig.10 AUG collision avoidance diagram

由此可知,当通过位置推算预测出AUG间存在互相碰撞情况时,优先级较低的AUG启用人工势场法进行避让,而优先级较高的AUG将不受影响,继续沿自身路径航行。相比之下,AUG优先级越低,路径调整的次序就越靠前,相应的协调范围也越大。

5 仿真分析

为验证所提基于双层协调体系的多圆碟形AUG三维路径规划方法的有效性,按照航行区域的不同海底情形,分一般和复杂2种海底地貌来讨论海流和碍航物影响下3艘AUG的路径规划。本文中圆碟形AUG的参数为：Pv=1.728 W,qv=0.011 4 L/s,Pa=10 W,qa=0.2 L/s,Bd=25.1 N,Ue=12 V,I0=0.2 A,ηm=0.8,qp=0.002 1 L/s,ηp=0.8,Pm=2 W,m=144.3 kg,mp1=4 kg,vp1=0.000 5 m/s,h0=0.005 m,Pc=2.6 W。整个仿真忽略AUG由于导航定位及路径跟踪控制误差所带来的实际位置偏差,将AUG对水航速设置为V=0.25 m/s,滑 翔 角 设 置 为Θ=35°。3艘AUG的优先级从高到低依次为 AUG1、AUG2和AUG3。

5.1 一般海底地貌下的路径规划

该地貌下二维环境被设计为在1 000×1 000的网格环境下随机分布2个粘性Lamb涡以及若干岛屿,BMC算法部分的参数设定为M=30,N=240,K=100。3艘AUG的起点和终点为：AUG1的起点和终点分别为(100,100,0)和(900,850,0),AUG2的起点和终点分别为(100,150,0)和(900,900,0),AUG3的起点和终点分别为(100,200,0)和(900,950,0)。

图11、12为多AUG集群在目标区域进行海洋作业,以能耗最优进行的多AUG路径规划。首先根据各AUG的起点与目标点及环境信息得出了全局路径规划的结果,为保证AUG航行安全,需进行路径的局部规划,利用全局规划的路径计算出AUG经过各路径点的时间,据此来确定存在碰撞的区域,根据AUG集群中的优先级次序来进行局部调整,因为3艘AUG集群中AUG1的优先级最高,AUG2优先级次之,AUG3的优先级最低,经过局部调整后的路径如图11中实线路径所示,由此可知,经过局部调整后的路径除了能实现对目标的优化外,还能够消除碰撞风险。图12为根据2种优化目标得到的三维路径,可以看出3组路径均能实现对水下复杂地形的避障,并可以实现避碰功能。

图11 多AUG能耗最优路径规划二维图Fig.11 2-D graph of multi AUG energy optimal path planning

图12 多AUG能耗最优路径规划三维图Fig.12 3-D graph of multi AUG energy optimal path planning

一般海底地貌下采用所提方法生成最终路径的航行能耗如表1所示。

表1 航行能耗数据Table 1 Data on voyage energy consumption

5.2 复杂海底地貌下的路径规划

真实的AUG作业环境往往更加复杂多变,为了进一步验证本文所提基于双层协调体系的多AUG路径规划方法在更为复杂海洋环境的有效性,以能耗最优作为优化目标,选取舟山市西南海域的复杂水下作业环境进行仿真验证。

BMC算法部分的参数设定为M=30,N=1 020,K=500。3艘AUG的起点和终点为：AUG1的起点和终点分别为(1 000,3 750,0)和(8 500,5 550,0),AUG2的起点和终点分别为(1 000,4 500,0)和(8 500,6 000,0),AUG3的起点和终点分别为(1 000,3 000,0)和(8 500,5 100,0)。

在航行深度H=80 m工况下的仿真结果如图13、14 所示。图13、14为AUG集群在完成海洋观测任务后返回近岸区域,以能耗最优规划出的3艘AUG的二维和三维路径。可以看出,根据各AUG的起点与目标点及环境信息,采用BMC方法能够实现真实复杂海洋环境下多艘AUG的全局路径规划。根据3艘AUG的不同优先级,经过局部调整后规划出的3组路径均能够实现真实复杂海域环境下的三维避障和避碰功能。

图13 多AUG能耗最优路径规划二维图Fig.13 2-D graph of multi AUG energy optimal path planning

图14 多AUG能耗最优路径规划三维图Fig.14 3-D graph of multi AUG energy optimal path planning

复杂海底地貌下采用所提方法生成最终路径的航行能耗如表2所示。

表2 航行能耗数据Table 2 Data on voyage energy consumption

6 结论

1)本文基于圆碟形水下滑翔机在水下航行时的工作原理及航行特点,建立了圆碟形水下滑翔机的能耗模型,并考虑了复杂海流对其能量消耗的影响,以能耗优化为目标,通过BMC算法求得能耗最优路径。

2)通过建立双层协调体系及避碰规则,在获得全局路径的基础上获得了既能满足全局能耗优化又能满足局部避碰的路径,实现了多圆碟形AUG的路径规划。

在下一步的工作中,将进一步完善圆碟形水下滑翔机的动力学模型,考虑路径规划下的路径跟踪,以进一步验证本文所提路径规划方法的有效性。