基于数据驱动的柔性立管骨架层多目标优化

阎军,张恒瑞,李文博,王心悦,卢海龙

(1.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023;2.大连理工大学 宁波研究院,浙江 宁波 315016;3.大连理工大学 工程力学系,辽宁 大连 116023)

柔性立管是海洋油气资源开发的关键输运装备之一,被誉为深水开发系统的“血管”[1]。柔性立管通常由多层金属与非金属层非粘结螺旋缠绕构成。金属层主要用于抵抗径向和轴向荷载,非金属层主要用于防止层间接触和内部液体泄漏。柔性立管最内层为骨架层,由异型钢带沿着近90°的方向螺旋缠绕制成,其作用为抵抗外部静水压力,防止柔性立管发生压溃失效。柔性立管在外压荷载下的工况可分为干压和湿压[2]。在湿压工况下,外部液体侵入柔性立管内部,直接作用于内护套层,此时主要由骨架层单独抵抗外部静水压力,这也是柔性立管的危险失效工况之一。

目前国内外学者通常采用等效模型并结合数值模拟的方法对骨架层临界压溃载荷开展评估。等效模型方法将具有复杂几何截面形状的骨架层等效成各向同性均质圆环,并根据压溃理论公式[3]求解临界压溃载荷。Zhang等[4]以骨架层截面面积为等效标准获得等效厚度;Neto等[5]以单位长度的弯曲刚度为等效标准获得等效厚度,并引入修正系数减少误差;汤明刚等[6]以压溃前后的应变能变化值为等效标准获得等效厚度,该方法可以保证预测结果趋于保守。由于等效模型难以准确考虑接触、摩擦等非线性因素[2],很多研究者选择数值模拟的方式对骨架层抵抗外压荷载的能力进行研究。Neto等[5]建立了考虑螺旋角度的三维完整模型与忽略螺旋角度的三维环模型,发现二者计算结果极为接近,因此在建模时可忽略螺旋角度。汤明刚等[7]计算了骨架层一阶屈曲特征值,并分析了椭圆度和材料弹塑性对骨架层临界压溃载荷的影响。任少飞[8]分析了螺旋铺设角度、层间接触、初始椭圆度等因素对骨架层临界压溃载荷的影响。Cuamatzi-Melendez等[9]考虑抗压铠装层支撑作用的影响,探究了网格数量及尺寸、模型长度、边界条件等因素对骨架层临界压溃载荷的影响。李鹏等[10]将加工残余应力作为初始缺陷引入骨架层有限元模型,探讨了残余应力对骨架层临界压溃载荷的影响。Liu等[11]以4个骨架层截面关键参数为设计变量,探讨了截面参数对其特征值屈曲的影响。

目前国内外学者的研究集中在探讨椭圆度、材料参数、厚径比等参数对骨架层临界压溃载荷的影响,但鲜有研究对骨架层截面构型参数进行优化。因此,本文开展骨架层参数化建模及非线性屈曲分析,揭示截面构型参数对骨架层临界压溃载荷的影响规律,由于非线性屈曲分析计算时间较长[9],使用传统优化流程效率较低,因此本文将数据驱动方法引入优化流程,开展多目标优化获得不同工况下的最优截面尺寸设计。

本文介绍了均匀外压下的均质圆环弹性失稳方程的理论解,并建立参数化骨架层有限元模型,开展非线性屈曲分析,并将仿真临界压溃载荷和实验临界压溃载荷进行对比。选择部分骨架层截面参数将其定义为设计变量,通过非线性屈曲分析获得对应临界压溃载荷,构造径向基(radial basis function,RBF)代理模型[12]并对参数进行敏感性分析,采用多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)算法[13],以骨架层最小质量和最大临界压溃载荷为目标开展多目标优化,为柔性立管的骨架层抗压溃设计提供理论模型和求解算法。

1 圆环弹性稳定性理论

目前管道在均匀外压下的弹性极限载荷主要是基于Timoshenko的弹性稳定性理论[3]开展计算。Timoshenko建立了中心线是圆弧的曲梁挠度微分方程,成为圆环弹性失稳问题解析基础：

(1)

式中：ω为径向挠度变形;θ为环向角度;M为施加在杆件截面的弯矩;R为曲率半径;EI为细杆的弯曲刚度。

图1 均质圆环受环压示意[3]Fig.1 Schematic diagram of homogeneous ring subjected to ring pressure[3]

M=M0-qR(ω0-ω)

(2)

将弯矩M代入到式(1),并根据结构对称性和环长固定条件,求得临界压溃载荷,如式(3),详细推导过程见文献[2]：

(3)

工程设计中通常采用式(3)计算薄壁圆环受均匀外压情况下的临界压溃载荷,但是该式既没有考虑材料塑性变形,也没有考虑结构缺陷的影响,并且忽略复杂截面构型间接触摩擦的影响,因此计算得到的结构临界压溃载荷存在较大误差[14]。

2 骨架层非线性屈曲数值模拟

骨架层抵抗外压荷载的能力可通过屈曲分析确定。屈曲分析分为特征值屈曲(线性屈曲)和压溃(非线性屈曲)。特征值屈曲对理想结构进行屈曲分析,获得结构的屈曲特征值和屈曲模态。但是由于材料非线性以及结构缺陷等制约,工程实际中的柔性立管的骨架层结构抵抗屈曲破坏能力会显著降低,因此需要对结构进行非线性屈曲分析,获得更为准确的结构临界压溃载荷。本文经通过非线性屈曲分析获得骨架层临界压溃载荷。

在骨架层有限元模型中,由于螺旋角度对临界压溃载荷影响很小[5,8],因此可忽略螺旋角度,将骨架层视为圆环结构,又因为模型具有对称性,有限元模型可进一步简化为1/4圆环结构。为考虑骨架层复杂截面构型影响,沿管道轴向至少需保留一个完整骨架层截面。为此,设计骨架层几何模型和截面参数分别如图2和表1所示,骨架层内径设为200 mm。

表1 骨架层截面参数Table 1 Names and size of cross-section parameters of carcass layer

图2 骨架层几何模型及截面参数示意Fig.2 Schematic diagram of the geometric model and cross-section parameters of the carcass layer

2.1 材料参数设置

材料弹塑性对骨架层临界压溃载荷有较大影响[7],为获得准确的骨架层临界压溃载荷,必须考虑材料塑性的影响。骨架层通常选取316L不锈钢,弹性模量为206 GPa,泊松比为0.3,材料塑性数据如图3所示。

图3 316L不锈钢真实应力-真实应变曲线[15]Fig.4 316L stainless steel true stress-true strain curve[15]

2.2 单元类型与网格收敛性验证

本文采用八节点六面体线性减缩积分单元(C3D8R),该单元可同时兼顾计算效率与精度,在骨架层非线性屈曲分析中可得到精度较高的评估结果[14,16]。

改变沿骨架层厚度和环向方向的单元数量进行网格收敛性验证,其结果分别如图4 (a)和图4 (b)所示。当厚度方向单元数量为2,环向单元数量为60时,结果趋于稳定。因此为兼顾计算效率和计算精度,本文采用如下方式划分网格：使用扫掠方法,沿骨架层厚度方向单元数量为2,沿骨架层环向单元数量为70,并使得骨架层截面单元长宽比接近1∶1,如图5所示。

图4 网格收敛性验证Fig.4 Mesh convergence verification

图5 骨架层网格示意Fig.5 Schematic diagram of carcass layer grid

2.3 接触及边界条件设置

骨架层相邻表面在外压作用下会发生接触滑动,为准确计算骨架层临界压溃载荷必须考虑摩擦的影响,本文将摩擦系数设为0.1[8]。根据文献[5],施加运动耦合如图6(a)所示,其中A耦合作用为模拟真实骨架层沿管道轴向的周期性特征,B耦合作用为模拟真实骨架层沿管道轴向的“无限长”特征。

图6 相互作用及边界条件设定Fig.6 Interaction and boundary condition setting

骨架层有限元模型的边界条件及载荷设定如图6(b)所示：在2个对称截面施加对称边界条件;选取对称截面上一单元结点限制其沿管道轴向自由度以避免刚体位移;在骨架层外表面施加均匀外压。

2.4 骨架层非线性屈曲分析

骨架层缺陷的常见表现形式为初始椭圆度[7],因此本文基于特征值屈曲结果,根据API 17B规范[17],初始椭圆度不应超过3%,本文施加2%的初始椭圆度,考虑几何大变形的影响,并选用弧长法[18]计算骨架层的临界压溃载荷。

通过骨架层特征值屈曲分析,得到一阶屈曲特征值为27.65 MPa,再对骨架层进行非线性屈曲分析,模拟得到的临界压溃载荷为14.79 MPa,相较一阶特征值下降46.49%。非线性屈曲分析过程中的载荷-位移曲线如图7所示,可以看到,在开始阶段,曲线呈现线性关系,表明此时骨架层仍处于弹性状态;随后曲线出现非线性趋势并达到峰值,在峰值点处骨架层处于临界压溃状态,此时对应的载荷值即为临界压溃载荷;然后结构继续变形,进一步降低了骨架层抵抗外压荷载的能力,从而使得载荷逐渐减小,此时骨架层已进入塑性压溃状态。图7中von Mises应力云图表明了不同阶段的骨架层状态。

图7 非线性屈曲载荷-位移曲线Fig.7 Nonlinear buckling load-displacement curve

基于上述的网格单元类型、网格数量与边界条件,根据文献[14]所给出截面及椭圆度参数建模并进行非线性屈曲分析,得到临界压溃载荷为16.26 MPa,与文献中实验值误差仅为6.97%。考虑到实验件存在加工残余应力、厚度分布不均匀等缺陷[14],本文构建的数值模型所得临界压溃载荷与实验值误差极小,验证了本文建模方法、网格划分等准确性。

3 构建代理模型

在深水应用时,柔性立管质量过大,会使柔性立管易发生轴向失效;而同时,过大的静水外压则可能引起柔性立管的压溃失效。因此本文以骨架层最大临界压溃载荷和最小质量为优化目标,建立数据驱动方法中的高精度RBF代理模型开展参数敏感性分析,并对骨架层截面尺寸参数进行多目标优化,得到优化问题的帕累托(Pareto)最优解集。

3.1 确定设计变量

由式(3)可以看出,内径不变时,圆环结构的临界压溃载荷与弯曲刚度成正比。如图8所示,在骨架层截面的各个参数中,参数L1、L2、L3、L4、L5、L6、R1、A1、t主要决定了骨架层的长度和高度,对截面惯性矩影响较大,而参数L7、A2、R2、A3、R3则主要用于保证相邻骨架层互相锁扣,对截面惯性矩影响较小。考虑到参数过多会使代理模型所需截面组合数量急剧增加,因此本文将分析参数L1、L2、L3、L4、L5、L6、R1、A1、t对骨架层临界压溃载荷的影响,其余参数取固定值,并同时设置参数L2与L6相同。

图8 骨架层截面关键参数(关键参数如粗体所示)Fig.8 Key parameters of carcass layer cross-section (The key parameters are shown in bold)

由于骨架层的截面构型十分复杂,使得在建模时参数尺寸范围难以确定,错误的范围将导致相邻骨架层截面发生“重叠”,从而无法生成骨架层几何模型。本文发现参数L4对骨架层截面是否发生“重叠”有着重要影响,因此本文将参数L4设置为因变量,这有利于几何模型顺利生成。各参数取值范围如表2所示。

表2 具体参数取值范围Table 2 The range of each parameter

3.2 实验设计

选取合适的取样方法至关重要。目前常见的取样方法有随机取样、正交取样、拉丁超立方取样及优化的拉丁超立方取样[19]等。正交取样方法采用数理统计学方法,选择有代表性的样本点进行计算,再参照“正交表”安排实验[20-22]。由于正交表具有均衡分散性和整齐可比性的构造原则,此方法设计的实验次数少,且能反映客观事物变化的基本规律[23],因此本文选用正交取样构造样本组合。

本文根据正交表,对该问题中参数L1取8个水平,L2、L3、L5、R1、A1、t各取9个水平,共获得81组截面组合,并通过非线性屈曲分析计算各截面组合的临界压溃载荷,计算时间约为54 h(4核3.7 GHz CPU,16 GB内存)。

3.3 构建代理模型及参数分析

代理模型可以在特定的输入与输出关系中,通过近似的函数映射关系代替复杂的真实映射关系[24],具有计算效率高、准确性高、模型泛化能力强等优点。目前常用的代理模型有响应面模型RSM[25]、径向基模型RBF、Kriging模型[26-27]等。RBF模型结构简单、训练简洁、学习收敛速度快、能够逼近任意非线性函数,并且具有较好的数值稳定性[12];另外由于RBF模型在处理多变量及非线性问题时具有突出优势,本研究构建RBF代理模型,对骨架层截面参数进行分析优化。

决定系数R2[28]是衡量代理模型误差的常用方法。R2的范围在0～1,其中1代表完全吻合。R2计算公式为：

(4)

本文将决定系数R2作为代理模型精度评判标准,通过随机取样方式重新构造45组截面组合,45组截面组合对应的有限元仿真临界压溃载荷-代理模型预测临界压溃载荷曲线如图9所示,本文构建的RBF代理模型预测临界压溃载荷的决定系数R2值为0.978,表明该代理模型预测精度较高,可以很好地反映骨架层临界压溃载荷与骨架层截面参数的关系。

图9 有限元仿真临界压溃载荷-代理模型预测临界压溃载荷曲线Fig.9 Critical collapse pressure simulated by finite element-critical collapse pressure predicted by surrogate model curve

基于RBF代理模型,对骨架层截面关键参数进行敏感性分析,各截面参数对骨架层临界压溃载荷贡献占比如图10所示,可以看出厚度t对骨架层临界压溃载荷起着决定性影响,对骨架层临界压溃载荷贡献占比达63.52%,参数L1、L2、L5也均大于5%。因此选取参数L1、L2、L5、t进一步分析其对骨架层临界压溃载荷的影响,结果如图11所示。

图10 骨架层截面参数对临界压溃载荷贡献占比Fig.10 Percentage contribution of carcass layer cross-sectional parameters to critical collapse pressure

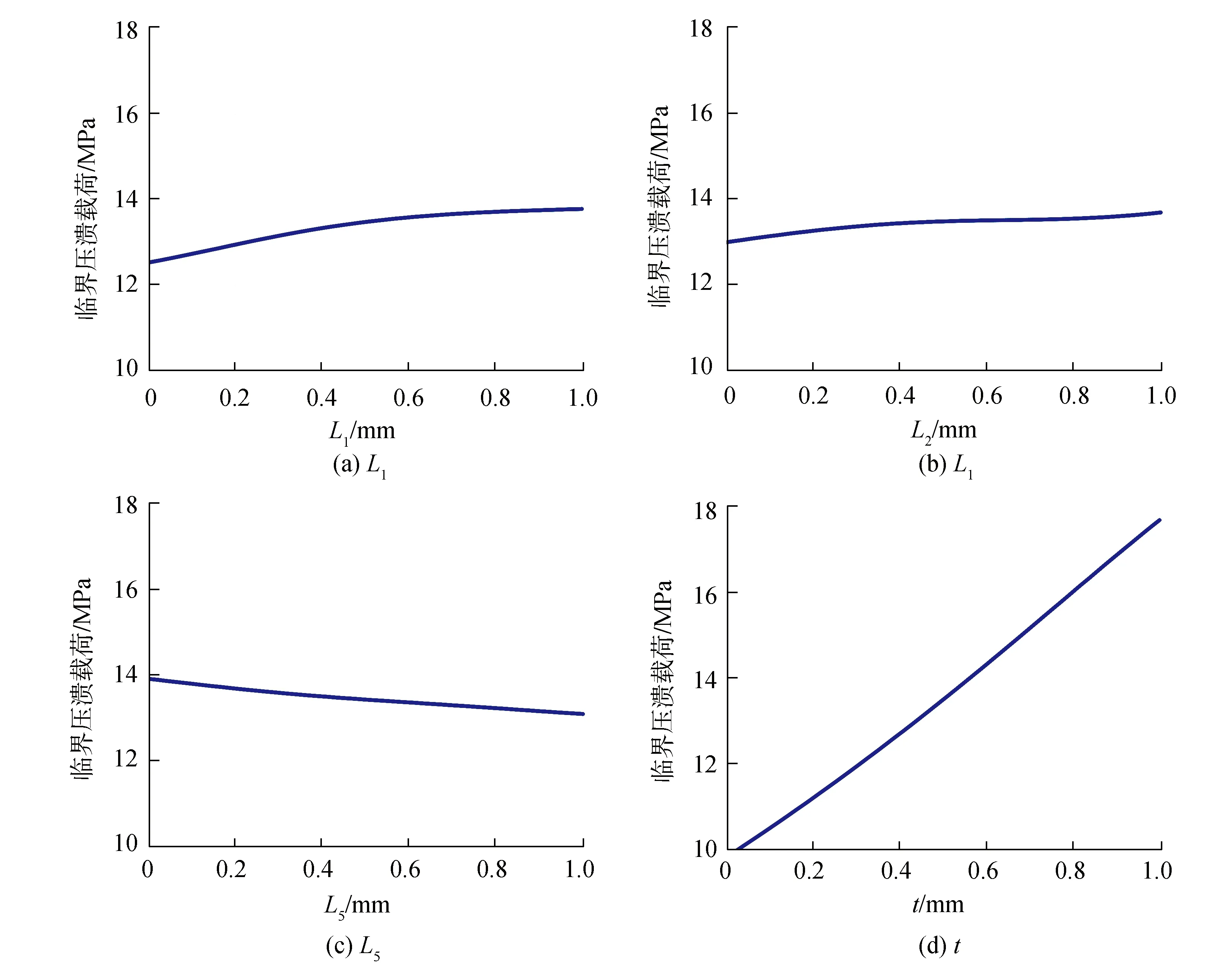
图11 关键参数L1、L2、L5、t对临界压溃载荷影响图Fig.11 Diagram of the influence of key parameters L1,L2,L5,t on critical collapse pressure

由图11可以看出,骨架层临界压溃载荷随着L1的增大而增大,L1增大到7.75 mm时,增长速度减缓;参数L2与临界压溃载荷呈正相关关系,临界压溃载荷随L2的增大而增大;随着参数L5的增大,临界压溃载荷减小;临界压溃载荷会随着厚度t的增大而显著增大,曲线接近于直线,表明临界压溃载荷与厚度t呈线性关系。

由于厚度t对临界压溃载荷有决定性影响,因此进一步分析厚度t与其他关键参数的耦合影响,其结果如图12所示,临界压溃载荷呈现平面状,表明厚度t与其他参数的耦合影响对临界压溃载荷影响较小,厚度t对临界压溃载荷有决定性影响。

图12 厚度t与其他参数耦合影响图Fig.12 Diagram of the influence of thickness t coupled with other parameters

3.4 多目标优化

对于多目标优化问题,多个目标函数之间是无法比较且往往是互相冲突的,实现一个目标函数的改进需要以牺牲其他目标函数的值作为代价。我们通常不可能找到一个设计,使所有分目标函数都达到不考虑其他分目标时该目标能达到的最优值。因此在多目标优化问题中往往包含多个解,即为Pareto最优解集。需要指出的是,通常来说,多目标优化问题的最优解只能是针对某一具体问题的满意解,即为Pareto最优解集中的有效解,此有效解即为此多目标优化问题中的最优解[28-31]。

本文采用MOPSO算法对骨架层截面进行优化,MOPSO算法基于粒子群优化算法处理多目标优化问题,粒子找到的最佳解决方案的历史记录可用于存储过去生成的非支配解方案,使用全局吸引机制与先前发现的非支配解历史方案相结合,将促使收敛到全局非支配解方案。研究表明MOPSO算法计算时间短,优化效果好[31-32]。

本文基于RBF代理模型,采用MOPSO算法,以骨架层最小质量和最大临界压溃载荷作为优化目标,优化如图8所示截面关键参数,获得多目标优化问题的Pareto最优解集。在优化问题中,通常需将最大值优化问题采取相应措施转化为最小值优化问题,由于压强的负数常表示为内压,常用的施加负号措施不适用,因此将最大临界压溃载荷优化问题转化为最小临界压溃载荷倒数优化问题。优化后得到优化问题的Pareto最优解集如图13所示。

图13 骨架层多目标优化问题Pareto最优解集Fig.13 Pareto optimal solution of the carcass layer multi-objective optimization problem

由图13可以看出,对骨架层进行多目标优化后得到的Pareto最优解集分布均匀,这表明优化后所得Pareto最优解集质量较好。本文考虑1 000、1 500和1 800 m这3种应用工况,得到3组最优截面参数设计及对应的临界压溃载荷和质量,如表3所示。通过非线性屈曲分析计算3组最优截面参数的临界压溃载荷,并与代理模型预测临界压溃载荷进行对比,如表4所示。可以看出,3种工况下,有限元仿真临界压溃载荷和代理模型预测骨架层临界压溃载荷误差均小于3%,满足工程设计的精度要求。

表3 1 000、1 500和1 800 m水深最优骨架层截面尺寸参数、代理模型预测临界压溃载荷及质量Table 3 Optimal carcass layer cross-sectional parameters,and predicting critical pressure and mass for surrogate models at 1 000,1 500 and 1 800 m water depth

表4 1 000、1 500、1 800 m水深工况下有限元仿真临界压溃载荷与代理模型预测临界压溃载荷对比Table 4 Comparison of critical collapse pressure simulated by finite element method and critical collapse pressure predicted by surrogate model for 1 000,1 500 and 1 800 m water depth

4 结论

1) 建立了骨架层有限元模型,开展了非线性屈曲分析并进行实验验证,基于非线性屈曲分析结果,构造了高精度的RBF代理模型。通过RBF模型开展了截面关键参数的敏感性分析,结果表明厚度对骨架层临界压溃载荷起着决定性作用,贡献占比达64.55%,因此增大厚度是提高骨架层临界压溃载荷的有效方法。

2) 采用MOPSO算法开展了最大临界压溃载荷和最小质量的多目标优化,得到Pareto最优解集,根据3种应用工况得到3组最优骨架层截面参数设计,并过有限元方法计算3组最优截面参数的临界压溃载荷,发现3组代理模型预测临界压溃载荷和有限元仿真临界压溃载荷误差均小于3%,满足工况设计的精度要求。

本文工作对提高柔性立管临界压溃载荷具有重要的工程指导意义,对推进我国柔性立管深水化提供了重要参考。