波浪反射系数计算方法的性能分析

张茴栋,张德康,张勇谋,史宏达

(中国海洋大学 工程学院,山东 青岛 266100)

波浪反射系数是建筑物或模型对波浪反射程度的指标,其值为反射波和入射波波幅之比,由于无法直接测量入、反射波波幅,所以相关研究者们提出了不少可行的计算方法。这些方法包括时域和频域方法,其中使用最多的是频域方法。Healy[1]提出了反射系数的计算方法,仅需使用一个波高仪沿波浪传播方向缓慢移动记录波形,此方法原理简单,但是极易受人为因素干扰,而且仅适用于规则波。Isaacson[2]使用2个固定位置的波高仪,避免了移动波高仪中可能的人为因素干扰,使用时只需计算合成波的波幅和波形相位差即可得到反射系数。Isaacson[2]还提出了无需计算相位差仅使用3个测点处的合成波波幅计算反射系数的方法,但误差较大。Isaacson的这2种方法同样仅适用于规则波。Goda等[3]提出了可以同时计算规则波和不规则波反射系数的方法,此法计算精度较高,在工程实践和科研中得到了广泛的应用。Mansard等[4]使用3个波高仪采集波浪序列,扩大了频率计算的范围,并且基于最小二乘法求解超静定方程组得到入反射波的波幅。

时域方法不仅能够计算反射系数,而且可以实时分离入反射波序列,因此在工程实践中也得到了广泛的应用。Zhu[5]基于线性系统理论,构造了波浪反射中的传递函数,并使用卷积等方法分别得到入反射波序列,但是此方法仅适用于规则波。Frigaard等[6]利用数字滤波技术,提出了不规则波的时域分离方法,其原理与Zhu[5]的方法基本相同,将2个波高仪采集的波浪序列作为输入信号,再与脉冲响应函数进行卷积得到入射波序列,但是其方法缺少反射波序列的分离计算。Sun等[7]将希尔伯特变换应用于反射系数的计算,将2个波高仪采集的波浪序列变换为解析信号,然后在时域中分离出入反射波序列。

然而在实际波浪场中,波浪中的非线性以及信号噪声的存在都会对计算结果产生影响,Frigaard等[8]研究了在规则波中,随机噪声、波浪非线性以及波高仪测量误差分别对Goda等[3]两点法和Mansard等[4]三点法的影响,并将2种方法的性能进行了比较。但是其工作仅限于研究规则波,所比较的方法也仅有2种,而且工况设置较少。本文基于数模与物模对不同波况下6种反射率计算方法的性能参数进行研究和对比,进而筛选出噪声和非线性干扰下性能表现依然最优的算法,这对港工建筑物结构的设计、防波堤消波性能的评价等领域具有重要的理论参考价值和实践指导意义。

1 数值模拟方法简介

1.1 规则波的数值模拟

在水槽中进行规则波试验时,由于造波机和采集仪器的性能不稳定,导致采集的波浪序列出现噪声,并且随着波陡的增大,波浪逐渐出现非线性。

为了更加真实地模拟实际中采集的规则波,依据信噪比将高斯白噪声加入余弦波序列,再通过非线性项公式给含噪波列引入非线性。图1为生成入反射波的数值水槽试验模型简图。

图1 入反射波生成模型简图Fig.1 The model of the generation of the incoming and reflected waves

Kris等[9]引入信噪比给模拟的波浪序列添加噪声,研究了噪声对Gaillard等[10]的阵列法计算反射系数的影响,并提出了一个数学函数用于计算结果的校正。本文也采用同样的方法给波列添加噪声。

信噪比反映了真实信号与噪声的比值关系,其幅值越小表明噪声含量越大。经过对比,发现信噪比为30～40 dB时,波列比较接近实际试验采集到的含噪波列。因此本文采用信噪比为40 dB和30 dB的合成波模拟低强度和高强度2种典型工况的含噪波列,加入2种噪声后的波形如图2所示。

图2 含噪声波形Fig.2 Waveform signals with noise

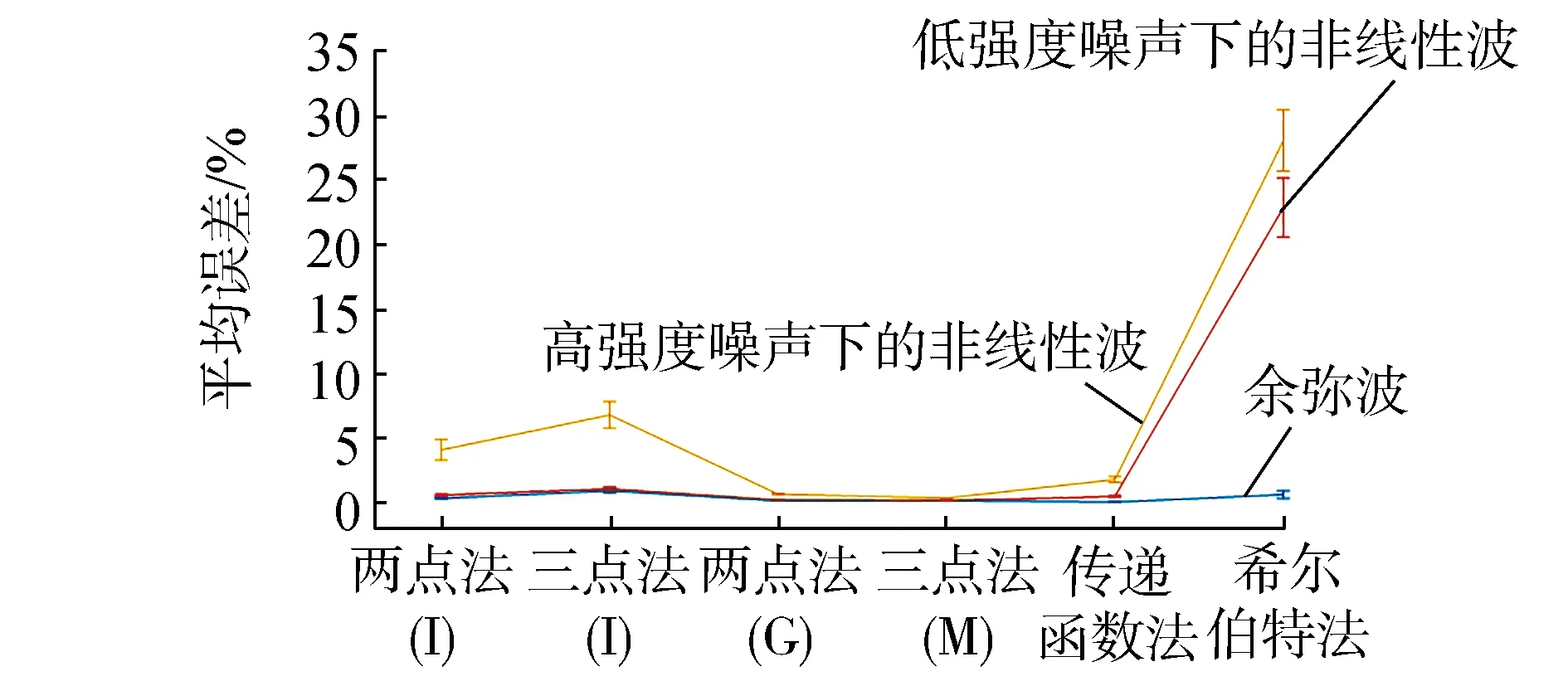
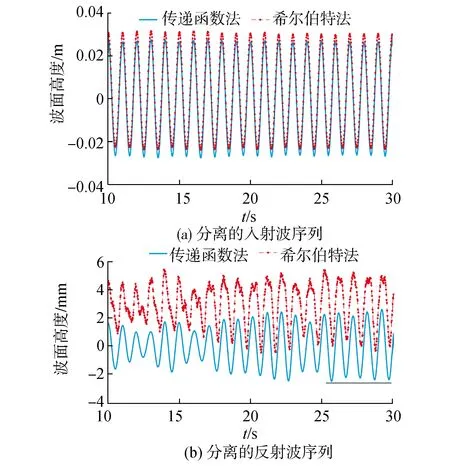
工程上常用的非线性波理论有斯托克斯波和椭圆余弦波理论。由于椭圆余弦波理论适用于浅水区(0.05

图3 非线性波形Fig.3 Nonlinear waveform

图4 各工况靶谱Fig.4 Target spectrum of each case

1.2 不规则波的数值模拟

工程中模拟不规则波的方法有很多种,但大部分都是基于线性波浪理论,常用的主要有2种：线性波叠加法和线性过滤法。本文使用线性波叠加法,通过模拟靶谱实现不规则波的内部构成。

2 数值模拟结果分析

2.1 数值模拟工况

2.1.1 规则波工况

模拟的余弦波周期分别为1、1.6和2 s,不同周期下分别对应3组入射波高,水深1 m,将反射率预设为0.1,各工况信息见表1。同时,将高、低强度噪声和非线性分别加入余弦波中,所有规则波数值试验工况共有27组。

表1 规则波工况参数Table 1 Parameters of regular waves

数值模拟的水槽长度20 m,采用4个测点(x1,x2,x3,x4)采集波浪序列。x1与造波机的距离为16 m,x4与反射结构的距离为1 m,以x1测点为参照,参考各种方法的最优间距,将波高仪间距设置为x1,2=0.6 m,x1,3=1.6 m,x1,4=3 m。

2.1.2 不规则波工况

本文的靶谱采用Jonswap谱,谱峰升高因子γ=3.3,峰形系数σa=0.07,σb=0.09。有效波高分别为0.08、0.09和0.1 m,谱峰频率分别为6.28,5.21和3.71 rad/s,频率下限为0.012 3 rad/s,高频截止频率为3倍谱峰频率,频率分段数N为512,水深1 m,将反射率预设为0.5,各组成波的入反射相位在[0,2π]内随机选取,共有3组工况,各工况参数如表2所示。

表2 不规则波工况参数Table 2 Parameters of irregular waves

不规则波数值模拟水槽的长度依然为20 m,水深1 m,采用4个测点采集波浪序列。x1测点位置与规则波中布局完全一致,参考Goda和Mansard对于不规则波波况中波高仪间距布置的建议,将其余3根波高仪按下述方式设置间距：x1,2=0.2 m,x1,3=0.5 m,x1,4=0.9 m。鉴于各种算法的最优间距还取决于测试工况,为了性能评估具有一般性,本文选择了所有算法在规则波测试工况均不失效的区间来统一布置波高仪。不规则波中波高仪间距的布置尽量保证其谱峰频率区域远离各种算法的失效区间。

2.2 结果分析

针对上述的不同工况,本文使用多种算法对反射系数进行计算并开展统计分析,从2个方面评价各个算法的性能：1)精确度,通过计算组合测点反射系数的平均误差来反映,误差越小,精确度越高;2)稳定性,通过计算所有误差的标准差来反映,标准差越小,稳定性越强。本文误差ε定义为：

ε=(Ri-R0)/R0

其中：Ri为求得的反射系数;R0为准确的反射系数。

2.2.1 规则波工况的结果分析

实际试验中的波列因存在噪声和非线性会与规则的余弦波有一定的差异。各反射率计算方法的原理各异,因而噪声和非线性会对其造成不同程度的影响。

为探究规则波工况下不同方法(Isaacson两点法、Isaacson三点法、Goda两点法、Mansard三点法、传递函数法和希尔伯特法)受此影响而引起的性能差异及变化。本文利用上述6种方法对含有一定强度的噪声和非线性波列进行研究对比(如图5所示,区分两点法和三点法时采用作者姓氏的第一个字母进行了标记)。3种波况下各种方法的性能表现如下所述。

图5 不同方法在规则波工况中的性能参数Fig.5 Performance of different methods in the regular sea states

1)余弦波。

各算法在余弦波中都具有较高的精确度,并且传递函数法和希尔伯特法都能准确地分离入反射波序列,虽然不同方法结果之间略有差异,但是基本可以忽略不计。

2)低强度噪声下的非线性波。

当对非线性波添加低强度噪声后,Isaacson两点法、Isaacson三点法、Goda两点法、Mansard三点法、传递函数法仍能保持较高性能,但希尔伯特法的误差出现明显增大的趋势。鉴于此时噪声较小,产生误差的主因必定为非线性,这一结论可以从具体的数据分析得到印证：在非线性作用下希尔伯特法的平均误差和标准差分别为21.1%、0.259;对其添加低强度噪声后,希尔伯特法的平均误差和标准差升至22.92%、0.288,因此可以确定非线性是造成希尔伯特法误差的主要诱因。

此外,为进一步揭示希尔伯特法性能明显下降的直接成因,将分离的入反射波序列与实际波列进行比较,以规则波工况2中波高为0.1 m的波形为例,其分离的波形如图6所示。

图6 希尔伯特法分离的入反射波Fig.6 Waves separated with Hilbert method

如图6所示,该方法对于入射波的分离基本准确,但是反射波的分离有较大的误差,波形带有扰动且向下平移,这会导致反射波的波幅计算失准,进而影响到希尔伯特法计算反射系数的精度。很显然,进行希尔伯特变换时,波列所含噪声和非线性等误差因素也一并参与变换,并且在分离出的反射波序列中得到进一步放大,致使反射序列失真,反射系数的计算偏差较大[12]。

3)高强度噪声下的非线性波。

当噪声上升至高强度时,各测点入反射波幅的计算会受到一定影响,图5中Isaacson两点法和三点法性能显著降低,Goda两点法和Mansard三点法由于使用了傅里叶变换减小了噪声和非线性的影响,仍旧保持较高精度,传递函数法也保持了较高性能,能够准确地分离入反射波序列,希尔伯特法随噪声强度增大表现更差。

综上分析,规则波中Mansard三点法、Goda两点法和传递函数法抗干扰性强,计算精度较高,Isaacson两点法和三点法对噪声较为敏感,高强度噪声时性能较差,希尔伯特法受非线性影响较大,性能最差。

2.2.2 不规则波工况的结果分析

鉴于Mansard三点法、Goda两点法和传递函数法在规则波工况中计算反射系数的优异表现,本论文将在不规则波工况中继续研究此3种方法的精确度,上述方法各自特点为：1)Mansard三点法计算频率范围更宽;2)Goda两点法由于受到奇异点的限制,计算频率需要进行前期优化;3)对于传递函数法,在设计滤波器时,由于将模值大于5的频率响应缩小为5,此法的奇异点不会破坏计算[6]。

各算法的性能参数如图7所示,经过比较可以发现,Mansard三点法性能最好,平均误差在5%左右,Goda两点法性能次之,传递函数法性能较差,平均误差高达35%。通过分析传递函数法分离的入反射波形可知,分离的反射波出现了较大的偏差,这是导致该方法在不规则波中失效的直接原因(以表2工况1为例,分离的波列如图8所示)。

图7 不规则波中各方法的性能参数Fig.7 Performance parameters of each method in irregular sea states

图8 传递函数法分离的不规则入反射波Fig.8 Separation of irregular incoming and reflected waves with transfer function method

3 物理模型试验

为进一步验证在数值分析中得到的各算法性能结果的准确性,本文以中国海洋大学海洋动力水槽为物理模型试验的基础,开展波浪反射系数计算方法的性能研究,水槽长60 m,宽3 m,高1.5 m。水槽末端为斜坡式结构,长5 m,高1.5 m,宽3 m,上面铺有一层厚度为10 cm的消波网。试验水槽的真实反射系数未知,本文将数模时表现最佳的Mansard三点法作为基准,与其他方法进行对比,进而评价其他方法在实际试验中的性能表现。

3.1 试验工况及仪器布置

3.1.1 试验工况

试验设置20组规则波工况,见表3,水槽的水深为1 m,采样间隔0.02 s,采样时长180 s,各周期分别设有4组波高。不规则波依然采用Jonswap谱作为靶谱,具体试验参数见表4。

表3 规则波工况参数Table 3 Parameters of regular waves

表4 不规则波工况参数Table 4 Parameters of irregular waves

3.1.2 试验仪器布置

依据波浪水槽的长度选取30～50 m处作为波高仪测量的区域,根据各个算法对波高仪间距的要求,结合实际波浪演化的情况,在规则波和不规则波试验中,将4根波高仪均以5 m的间隔等距排布,具体仪器布置见图9。

图9 物理模型试验仪器布置Fig.9 Layout of the instrument in physical model test

3.2 模型试验结果分析

3.2.1 规则波结果分析

去除失效间距的波高仪组合后,6种方法在规则波工况下计算的反射系数如图10所示。

图10 规则波工况反射系数的计算结果Fig.10 Result of reflection coefficient in regular waves

总体来看,在短周期工况(1 s、1.2 s)时,随着波陡的增大,反射系数也随之增大;在长周期工况(1.4、1.6、1.8 s)时,随着波陡的增大,反射系数趋于恒定并维持在较低的水平。同时也可以发现：反射系数随着波浪周期的增大总体呈现减小的趋势,表明水槽消波效果逐渐增强。因此可以判断斜置消波网对长周期波浪的消波效果更为明显。

由于水槽实验的真实反射率未知,本文以数值模拟时表现最佳的Mansard三点法作为基准,计算其余各算法的平均误差和标准差,结果如图11所示。Goda两点法和传递函数法在规则波工况下平均误差和标准差较低,表明2个方法的性能较好且精度接近。Isaacson两点法和三点法受到噪声及非线性的干扰,计算精度都有不同程度的下降,由于Isaacson两点法使用了傅里叶变换计算测点间的波形相位差,所以偏差比通过波形进行直接计算的三点法明显减小。希尔伯特法的平均误差和标准差最高,代表其性能最差,其原因为此方法在对所测波列进行希尔伯特变换时,不仅无法屏蔽噪声和非线性的影响,而且会放大其效应,导致反射波序列含有这些误差,进而出现反射系数计算偏差过大的现象。

图11 5种方法性能参数Fig.11 Performance parameters of five methods

以上结论与分析数值模拟的规则波时所得结果基本一致,可以相互验证。此外,本文对以上方法中仅有的2种时域方法(传递函数法、希尔伯特法)进行了入反射波序列的比较,具体示例见图12。2种时域方法对于入射波分离的结果基本一致,波高也都接近造波输入值(忽略造波板水力传递函数的影响),但是反射波有巨大的差异,希尔伯特法不仅带有剧烈的波形扰动,而且整体出现大幅偏移的现象,因此希尔伯特法的误差主要来自于反射波。相比于希尔伯特法,传递函数法可以消除直流分量导致的波列总体抬升[13],其分离的入反射波序列基本关于静水面对称,所以传递函数法比希尔伯特法更适合实时分离入反射波的波列。

图12 时域方法分离的入反射波Fig.12 Waves separated with two time domain methods

3.2.2 不规则波结果分析

为探究Mansard三点法、Goda两点法和传递函数法在分离实际的不规则入反射波时的性能表现,本文采用以上3种方法对表4的不规则波工况进行了反射系数的计算,具体结果参见表5。

表5 不规则波工况结果分析Table 5 Analysis of irregular waves

Mansard三点法计算的总体反射系数为0.083、0.101,若以Mansard三点法的计算结果为参考基准,可以发现传递函数法的计算值误差较大,分别达到57.8%和72.3%,而Goda两点法的计算值误差则为19.3%和23.8%。在高海况时,3种方法的计算偏差明显增大。这些性能差异与前面的数值分析结果保持一致。因此依据本文的研究,建议在不规则波中计算反射系数时优先选择Mansard三点法和Goda两点法。需要分离时间序列时可以采用传递函数法,其入射波列较为准确,但在高海况时需要注意分离出的反射波列,其波形可能失真程度较大。

4 结论

1)在规则波中,Mansard三点法、Goda两点法和传递函数法性能优于其它算法,在计算反射系数时具有较高的精度和稳定性;Isaacson两点法和三点法受噪声干扰较大,希尔伯特法对非线性较为敏感。

2)对于不规则波,Mansard三点法性能最好,Goda两点法性能次之,传递函数法性能变差。相比Goda两点法,Mansard三点法在计算时有效频率范围更宽,且由于使用最小二乘法求解波幅进一步缩小了误差。传递函数法计算反射系数的误差主要来自分离的反射波序列,入射波分离较为准确。

3)本文中数模和物模的分析结论基本一致。物理模型试验中,短周期时随波陡的增大,反射系数呈现增大的趋势,长周期时反射系数基本不随波陡的变化而变化。