基于改进垂向流量交换的城市内涝模拟方法
金 溪,周鹏飞,张翔凌,刘承宇
(武汉理工大学土木工程与建筑学院,湖北 武汉 430070)
近年来随着极端暴雨灾害的频繁发生,越来越多的城市开展了排水防涝规划与建设工作。在这个过程中城市内涝水文水动力模型得到了越来越广泛的应用[1-4]。早期水文水动力模型侧重于地面产流过程及地下管网水动力过程的模拟,无法模拟地面内涝[5]。为弥补这一缺陷,Hsu等[6]采用SWMM模型与地表二维模型耦合实现了城市内涝耦合模拟。但该方法中模型间的水流交换是单向的,当管网超载时,水流从检查井溢出到地表;当地下管网有足够过流能力时,地表水流不能回流至管网中。随着研究不断深入,逐渐出现一批能够实现地下地表水流双向交换的耦合模型[7-9]。耦合模型虽然具有结果详细、擅长处理方向不定水流模拟的优势,但计算过程复杂、计算效率低。为了达到模拟精度与计算效率之间的平衡,部分研究者开始探索既能避开求解繁琐物理方程又具有良好精度的内涝模拟方法,例如基于GIS 的淹没分析算法、改进填洼算法的洪涝计算以及部分简单元胞自动机模型[10-12]。但这些方法只能确定淹没范围和水深,不能模拟洪涝演进的水动力过程,因此应用范围有限。
目前耦合模型是城市内涝模拟的主要方法。垂向流量交换是耦合水文水动力模型的关键环节,对模拟结果的准确性及水量平衡会产生重要影响[13-15]。目前的垂向流量交换主要以一维模型节点水位(H1D)、二维模型地面水位(H2D)之间的差值为作用水头,利用孔口或堰流公式计算一维模型与二维模型之间的交换流量。该方法计算过程复杂并且独立于一维模型,没有考虑垂向交换流量与管道流量间的相互影响,容易造成计算不稳定,需要通过设置最大允许回流量等措施实现耦合计算的稳定性。
本文将节点进出水量平衡原则引入垂向流量交换计算过程,对耦合模型进行改进,简化垂向流量交换计算过程,提高耦合模拟的稳定性。采用理论案例及实际案例对改进方法进行验证,分析改进模型的可靠性和模拟精度,以期为耦合模型垂向流量交换提供一种新方法。
1 水文水动力耦合模型
对于耦合模型的耦合方式,国内外已有学者提出了一些较为符合实际的耦合理论并构建了耦合模型。耦合模型中一维、二维模型的时间同步以及水量交换是耦合方法的关键。对于一维管网模型与地表二维模型耦合,主要存在垂向水流交换,即水流在检查井、雨水篦处的交换;对于一维河网模型与地表二维模型耦合,水流交换主要存在水平方向上的正向交换和侧向交换。
本研究着重讨论一维管网模型与地表二维模型间的耦合过程。耦合模型中一维模型采用SWMM作为水文水动力计算引擎进行地表水文及管道系统水动力计算;二维模型采用守恒型浅水方程作为控制方程,利用自主开发的二阶Godunov格式有限体积法求解模块进行求解。
2 改进垂向交换流量计算方法
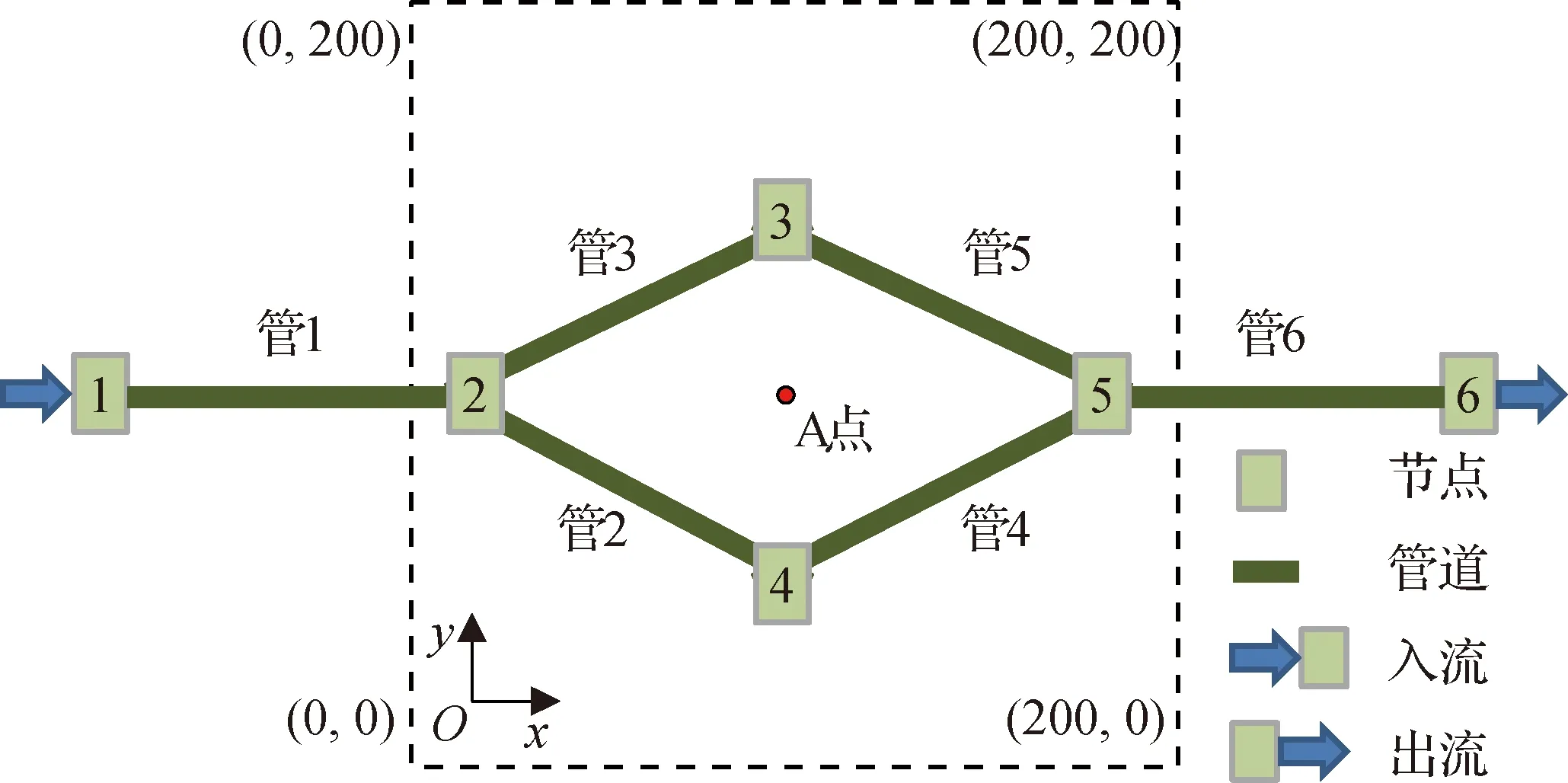
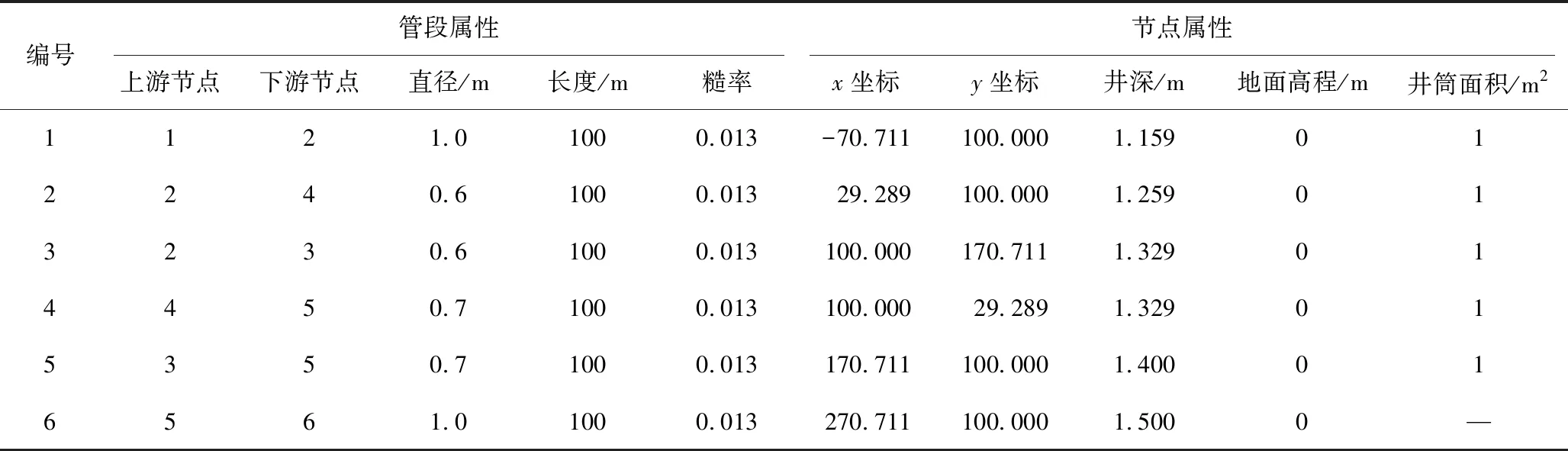
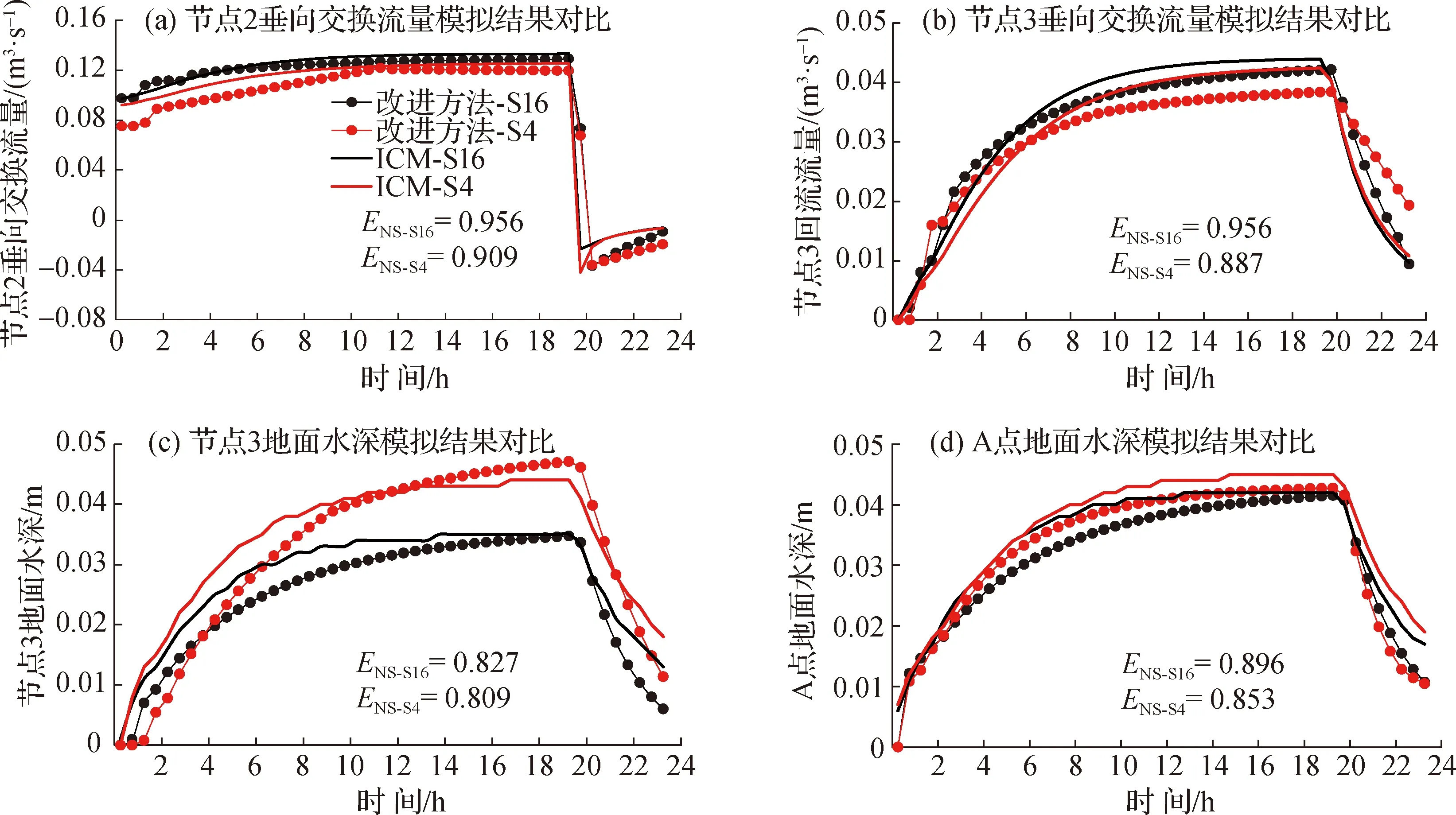
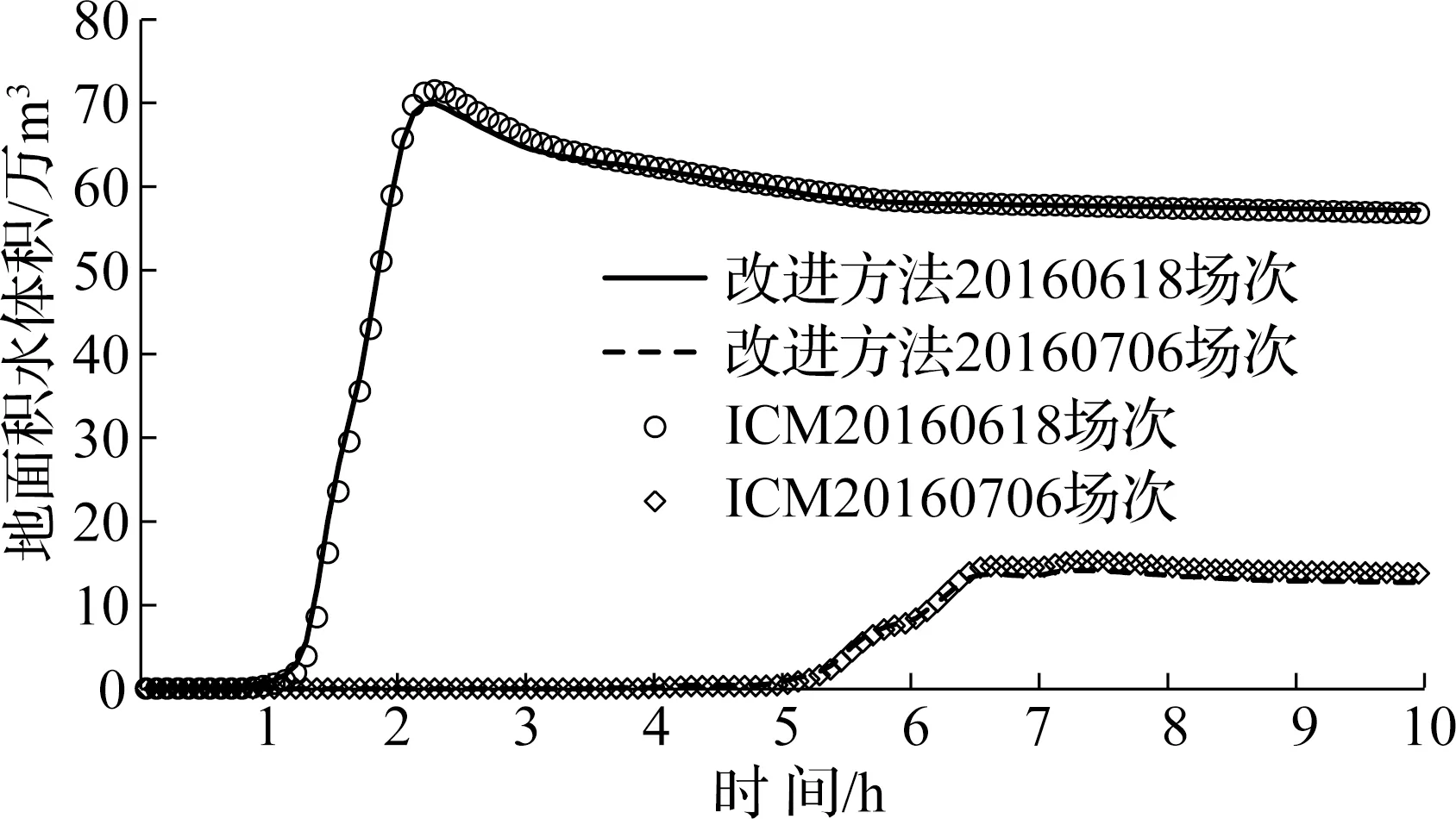
节点垂向流量交换的3种典型情况如图1所示。图1(a)、图1(b)表示节点超载情况(节点井内承压且节点水位(HJ)大于节点相连管段的管顶高程点最大值(HP),由于一维模型一般忽略节点井筒内空间,此时也表示一维节点水位超过地面高程(H0)),此种情况下一维模型管段流量的求解应该考虑节点位置处二维模型地表水位,并且通过管段流量的计算结果获得节点的入流量(Qbf)及出流量(Qof)。出流量为节点出流管段的流量之和,入流量包括节点入流管段的流量、地表径流流量、其他进流量等,将入流量及出流量的差值作为垂向交换流量,垂向交换流量大于0则代表溢流,小于0代表回流,等于0代表没有垂向流量交换。图1(c)表示节点未超载情况(HJ 图1 节点垂向流量交换的典型情况Fig.1 Three typical scenarios of node vertical exchange flow 将一维模型节点与其所在的二维模型地表单元格进行关联,方法是将地表单元格面积作为节点的积水面积,展示节点积水面积与地表单元格之间的关系,如图2所示。图2中,深蓝色单元格为节点所在位置对应的地表单元格,耦合模拟开始前利用该单元格面积更新对应节点的积水面积,该单元格除参与二维模型计算外还参与垂向流量交换的计算。其余单元格为普通单元格,只参与二维模型计算。 图2 节点积水面积与地表单元格关系Fig.2 Relationship between node ponded area and cells of 2-D mesh grid 2.1.1 节点超载情况下垂向交换流量的计算 当节点处于超载状态时,相连管道流量的计算需要考虑地表水位的影响,在一维水力模拟每个时间步长动力波计算开始之前利用节点所在地表单元格水位更新节点水位,然后执行动力波水力计算,从而实现考虑二维模型中地表水位变化情况下的一维模型水力模拟。利用节点进出水量守恒原则计算节点的垂向交换流量。根据水量守恒原则,节点积水面积内水体积变化与节点相连管段流量之间存在如下关系: (1) 式中:Vold为时间步长开始时刻节点积水面积内积水体积,m3;Vnew为时间步长结束时刻节点积水面积内积水体积,m3;Δt1D为一维模型时间步长,s;Qi为与节点相连管道的流量,m3/s,入流为正,出流为负;Qlat包含地表径流量、旱季流量等其他进流量之和,m3/s;m为节点相连管道的数量。 一维模型中节点积水面积内的水体积变化为一维、二维模型之间流量交换的体积,即 (2) 式中:Qexf为垂向交换流量,m3/s,正值表示节点溢流,负值表示节点回流。 2.1.2 节点未超载情况下垂向交换流量的计算 当节点不超载但地面有积水时,相连管道流量的计算不需要考虑节点位置处地表水位的影响,因此不进行节点水位的更新,仅计算节点回流流量。本文采用底孔口流量公式进行回流流量的计算,回流过程中地表水位会发生变化,采用式(3)所示的变水头流量公式作为回流流量计算的基础公式: (3) 式中:t为回流时间,s;S为积水面积,m2;H1为回流时间t起始时刻节点水位,m;H2为回流时间t结束时刻节点水位,m;μ为孔口流量系数,取值为0.62;A为节点井筒或雨水口面积,m2。 假设H2=0,利用式(3)求出节点所在单元格地面积水全部回流所需时间t。如果t>Δt1D,说明当前SWMM时间步长内单元格内积水没有全部回流,利用式(4)、式(5)计算当前时间步长结束时刻地面积水水位及回流流量: (4) (5) 如果t≤Δt1D,说明当前SWMM时间步长内单元格内积水全部回流,利用式(6)计算当前时间步长结束时刻回流流量: (6) 如果在时间步长结束时节点为超载状态,说明节点在该时间步长内由回流状态转化为溢流状态,此时节点的垂向交换流量采用进出水量守恒原则利用式(2)进行计算。 2.1.3 修正节点水位更新造成的连续性误差 图3 节点水位更新引起水量不平衡原因示意Fig.3 Diagram of continuity error caused by node head updating (7) 采用改进垂向流量交换计算方法耦合模型中的SWMM模型需要开启节点积水功能(启用Allow Ponding)。在Δt1D对应的耦合过程中具体计算步骤如下: (1) 根据展示的3种情况进行节点是否超载判断; (2) 超载节点进行水位更新操作,未超载节点进行回流流量的计算; (3) 一维模型演进一步; (4) 根据水量守恒原则计算超载节点垂向交换流量; (5) 连续性误差消除; (6) 垂向交换流量传递给二维模型; (7) 二维模型演进至Δt1D结束时刻。 由于SWMM模块具有计算节点积水体积变化的功能,节点超载情况下的垂向交换流量可以通过SWMM节点积水体积的变化直接获得。上述计算步骤中的(1)—(5)步可通过向SWMM模块添加相应的函数在SWMM模块内完成,降低一维、二维模型间耦合度,使得2个模块更加独立。 采用如图4所示的理论案例对改进方法进行验证。管网系统由6个节点和6根管道组成,地表区域为一个边长为200 m的方形闭合平原区域。平原区域覆盖的节点2—节点5均允许垂向流量交换,管道和节点的属性信息如表1所示。平原高程为0 m,糙率为0.025。水流通过节点1进入系统,入流量在模拟开始的10 min内由0逐渐增加至1.0 m3/s,然后保持不变至第20 h,然后降为0;水流通过节点6离开系统,出口设置为自由出流。系统初始为干,即管道和平原的初始水深均为0 m。 图4 理论案例示意[16]Fig.4 Diagram of theoretical case 表1 管网要素属性表 利用Infoworks ICM软件建立理论案例模型作为对照。ICM模型采用堰流公式进行垂向流量交换计算,堰流系数取值0.36。在改进垂向流量交换方法中节点所在单元格的面积会作为节点的积水面积,因此,网格划分对于耦合计算产生的影响需要进行讨论。采用2种单元格面积(4、16 m2)进行理论案例网格划分。 图5(a)展示了单元格面积16 m2网格划分下改进模型的水量平衡情况。在垂向流量交换过程中节点溢流量应该等于地面积水量与节点回流量之和,通过图5(a)可以看出改进模型在垂向流量交换过程中保持了水量守恒,节点累积溢流曲线与“节点累积回流+地表积水”曲线几乎完全重合。在一维、二维耦合模拟过程中,进入耦合模型的总水量应该等于流出系统的水量及在模型中积水水量之和。通过图5(b)可以看出模型整体水量平衡也得到了很好的满足。 图5 改进模型水量平衡分析Fig.5 Analytical diagram of water balance of improved model 图6以节点2为典型溢流节点,节点3为典型回流节点,A点及节点3位置作为地面淹没深度代表点,展示了2种网格划分(S4(网格面积4 m2)、S16(网格面积16 m2))情况下改进模型与ICM模型计算结果的对比。利用纳什效率系数(Nash-Sutcliffe efficiency coefficient,ENS)对2个模型模拟结果的吻合程度进行量化评价。通过对比可以看出,采用不同网格划分情况下改进垂向流量交换方法的计算结果与ICM模型模拟结果吻合度较高。在米级、十米级地表单元格划分条件下,采用改进垂向流量交换方法获得的耦合计算结果与ICM模型获得结果基本一致。通过图6(c)看出,网格划分的不同对于地面积水深度的模拟结果有一定影响,但是在不同网格划分的情况下改进方法均可以获得与ICM模型几乎吻合的地面水深变化曲线。 图6 改进模型与ICM模型计算结果的对比Fig.6 Comparison of improved model and ICM model results 采用武汉市武昌区东沙汇水子系统作为城市内涝模拟案例,研究区域管网汇水范围为82.73 km2。汇水区域内地势比较平坦,南侧为沙湖与东湖,湖泊为雨水的主要受纳水体,由于湖泊水位常年保持在较高水位,对于雨水入湖造成一定的影响,在局部低洼地区容易发生内涝。 利用Infoworks ICM及改进模型分别建立研究区域耦合模型。ICM模型地面网格采用非结构网格,单元格平均大小为450 m2,单元格数量为21万个。改进模型地面网格采用结构化网格,单元格尺寸为20 m×20 m,单元格数量为24万个。降水数据采用当地2016年6月18日及7月6日的2场暴雨(以下简称20160618场次、20160706场次),2场暴雨的累计降水量分别为143.5、125.6 mm,降水强度过程线如图7所示。 图7 暴雨降水强度过程线Fig.7 Research region storm system network and rainfall intensity curves of selected storms 采用改进垂向流量交换方法的耦合模型对于2场降水进行模拟后获得的地面淹水情况如图8所示。20160618场次降水量大、降水历时较短,导致了比较严重的城市内涝,模拟结果可以看出地面积水点较多、积水深度较深,积水范围与当日实际记录的内涝点基本吻合。20160706场次虽然降水量也比较大,但是降水历时较长,并且在降水过程中雨量分布比较均匀,峰值降水强度约为20160618场次峰值雨强的一半,因此形成的内涝较轻,当日记录的内涝点较少。通过模拟结果可以看出,采用改进垂向流量交换方法的耦合模型可以比较准确地模拟地面内涝淹没范围及深度。 图8 2场暴雨地面淹水情况模拟结果Fig.8 Flood areas of simulation results of two selected storms 图9 不同模型地面积水体积时间过程线对比Fig.9 Comparison of flood volume-time curves of different models 图9展示了改进方法模型与ICM模型在2场降水情况下地面积水体积随时间变化的情况。可以看出,改进方法模型与ICM模型的垂向流量交换计算结果几乎一致,地面积水体积随时间变化的曲线重合度较高,说明改进方法节点垂向流量交换计算结果与ICM模型计算结果吻合度较高。 在城市内涝模拟场景中超载节点的垂向流量交换数量占了总体垂向流量交换数量的绝大多数。通过对模拟结果的统计,在2场暴雨模拟过程中超载节点垂向流量交换数量占总垂向流量交换节点数量的比例分别为81.43%和88.66%,采用改进方法可以在绝大多数情况下利用SWMM模块通过水量守恒原则直接计算出节点的垂向流量交换结果,仅在少量的非超载节点回流情况下需要对回流流量采用变水头孔口流量公式进行计算。从而大大减少了采用孔口或堰流公式进行垂向流量交换的数量,提高了耦合模拟的计算效率及计算稳定性。 以SWMM 模型与自主开发的二维水动力模型为基础,构建城市内涝水文水动力耦合模型,在此基础上采用节点水量平衡原则对垂向流量交换方法进行改进。采用理论管网及城市排水管网作为案例,对改进方法从模拟精度、可靠性及水量平衡等方面进行了验证。主要结论如下: (1) 通过水量守恒原则计算节点垂向流量交换可以极大减少孔口或堰流相关的计算,计算过程可以由SWMM计算模块完成,简化了耦合模型的垂向流量交换的计算复杂程度。 (2) 非超载情况下的节点回流量计算通过增加相关函数的方式融合在SWMM计算模块中。SWMM模块在计算过程中采用迭代方法计算节点水头及管段流量,并以节点水头收敛为迭代停止条件,实现了节点垂向流量交换与管段流量的计算稳定性,避免出现节点溢流、回流交替出现的数值震荡现象。 (3) 通过与主流耦合模型软件infoworks ICM模拟结果进行对比,表明采用改进垂向流量交换方法的耦合模型具有良好的精度和可靠性,在米级、十米级、百米级地表网格划分情况下与infoworks ICM模拟结果高度吻合,可应用于城市内涝数值模拟计算。
2.1 垂向交换流量计算





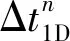
2.2 模型耦合实现方式
3 案例分析
3.1 理论案例

3.2 城市内涝模拟案例


4 结 论

