冰盖下水流紊动特性试验研究
陈 刚,董增川,王海军,顾世祥,杨红宣
(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.云南省水利水电勘测设计研究院,云南 昆明 650021;3.昆明理工大学电力工程学院,云南 昆明 650500)
河冰是陆地冰冻圈的重要组成要素[1-2],尽管覆盖范围相对较小,但对人类社会的影响却最为显著[3]。河冰生消演变会改变河流中物质、能量的输移规律[4-5],在特定的水文气象、河势和水力条件下甚至造成冰凌灾害,危及沿岸人民的生命财产安全[6]。中国陆地冰冻圈占陆地国土面积的78%[1],冰情影响范围广,冰凌灾害频发[7]。冰盖是河冰的重要存在形式,结冰盖输水是中国长距离调水、灌溉渠系工程实现冬季安全输水的常用运行方式[8]。冰盖形成附加的无滑移边界对河渠水流紊动特性的影响是河渠冰凌灾害防治、输水渠系冰期运行、调水工程设计与运行调度的重要理论基础。因此,研究冰盖下水流紊动特性对自然灾害防治和供水安全保障具有重要意义。
根据河冰生消演变对水流表面的影响,水流流态可分为明流、完全冰封和部分冰封[4,9]。部分冰封是指水流表面部分被冰覆盖(称为冰盖区),部分为自由水面(明流区),是前2种流态相互转换的过渡流态,岸冰是其主要存在形式。在水流紊动特性方面,相比明渠流已取得系统性研究成果,冰盖下水流的研究相对较少,尤其是部分冰封。早期研究侧重于揭示河冰生消的机理[10],仅有少数研究者通过原型观测分析冰盖形成对流速分布和输水能力的影响[11]。随着先进实验仪器的问世和室内试验条件的改善,国内外学者开始通过水槽试验研究冰盖下水流的特性。Parthasarathy等[12]探究完全冰封水流纵向时均流速、雷诺应力和紊动能的分布规律;陈建国等[13]测量不同冰盖组合下的水流结构,探讨冰盖流的输水能力;拾兵等[14]研究不同流速、水深、冰盖糙率条件下完全冰封水流的纵向紊动强度,发现冰盖下水流纵向紊动强度比明渠流大;Peters等[15]测量岸冰下水流冰盖区和明流区的纵向流速分布,发现岸冰形成使流动核心区向明流区收缩,导致明流区流速增加,冰盖区流速减小;Nyantekyi-Kwakye等[16]采用PIV技术测量不同宽度岸冰下水流瞬时流场,用于检验4种边界切应力计算方法的适用性;Wang等[17]测量岸冰下水流流速分布,用于校验冰盖下水流横向流速分布准二维模型。可见,现有的研究多针对单一流态,对比研究3种流态紊动特性的成果还较少。
本文在国内外已有研究成果的基础上,通过水槽试验测量3种流态的恒定均匀流场,从纵向时均流速、雷诺应力和紊动强度等方面分析冰盖对水流紊动特性的影响。
1 试验装置和研究方法
1.1 试验装置
试验在昆明理工大学水流与水工结构重点实验室的自循环玻璃水槽试验系统中进行,该系统由地下水池、泵站、量水堰、稳流池、水槽和回水池组成,见图1。水槽采用有机玻璃制作,长15 m,宽0.80 m,深0.35 m,纵坡坡降固定为0.5‰。水流通过泵站从地下水池提升至进水渠,经量水堰进入稳流池,溢流后进入玻璃水槽,从水槽尾门出流后经回水池进入地下水池,形成水流循环。为保证水槽的水流流态稳定,水槽进口端为深1.4 m、长4.5 m、宽6.5 m的稳流池,通过调节水槽末端的尾门来控制水槽中的水位,使水槽保持恒定均匀流。量水堰为无侧收缩矩形薄壁堰,用于测量流量,堰上水头由精度为0.1 mm的水位测针测量得到。流速采用挪威诺泰克公司(Nortek AS)生产的声学多普勒点式三维测速仪Vectrion测量得到。
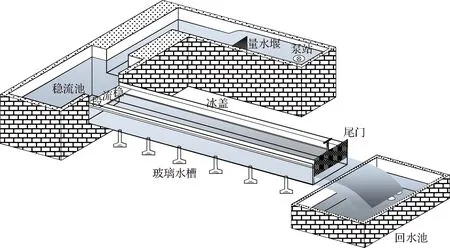
图1 试验装置示意Fig.1 Sketch of experimental set-up
1.2 试验材料
试验探究冰盖下水流的紊动特性,典型过流断面见图2(a),其中,B为断面宽度,b1为单侧冰盖的宽度,H为水深。以冰盖边缘为界划分为冰盖区和明流区,则断面冰盖覆盖度定义为F=2b1/B,当b1=0时,F=0;当b1=B/2时,F=1,即明流、完全冰封可视为冰盖覆盖度分别为0、1的特例。试验以F为变量,共设计6种工况,F值分别为0、0.250、0.375、0.500、0.750、1.000,详见表1。
在普通实验室中开展冰盖下水流水力特性研究,通常采用模拟冰盖替代真冰进行水槽试验,利于形成稳定流场。采用购置成本低、制作简便的成型单块泡沫板制作模拟冰盖,使用火把T2型电热丝泡沫切割机将泡沫板切割成长2.00 m,厚0.05 m,宽分别为0.10、0.15、0.20、0.30和0.40 m的条板。为确保水槽进口水流流态平顺稳定,距进口0.80 m段为槽内稳流段(图1),同时为避免尾门调节影响模拟冰盖,距尾门0.20 m段不布置冰盖,布置模拟冰盖的渠段长14.0 m,每种工况各准备14块泡沫条板。

图2 冰盖下典型过流断面和试验测量断面布置示意Fig.2 Sketch of a typical under-ice section and measuring cross section
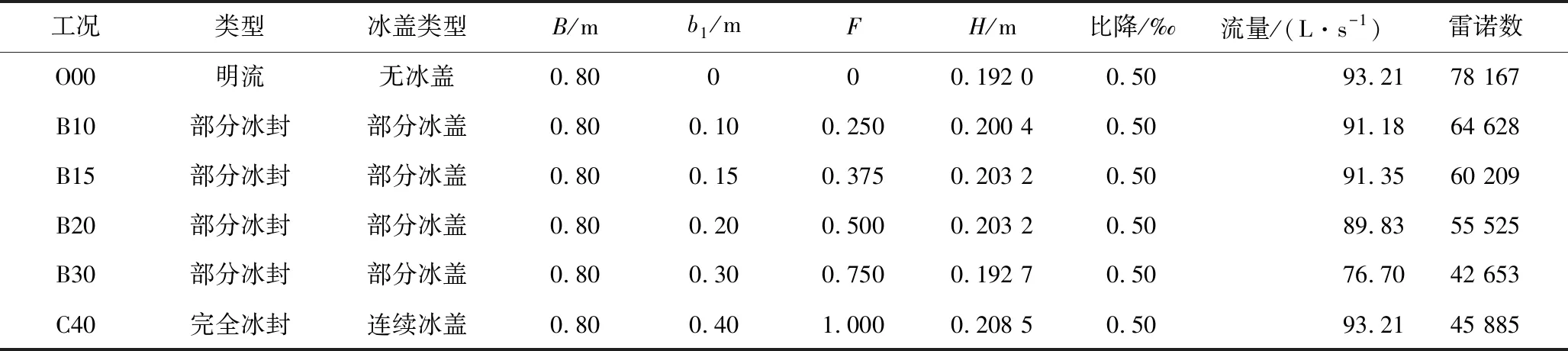
表1 试验工况
1.3 试验方案
试验时贴近水槽边壁布置切割好的泡沫条板,并利用水槽横梁上的旋转螺丝杆进行固定,使其贴近水槽边壁,不能随流波动,但能上下浮动。同时,由于真冰和泡沫板密度差异较大,通过旋转螺丝杆施加垂向压力,使泡沫板浸没在水中的深度与同体积真冰的浸没深度相等。
为确保试验在准恒定均匀流条件下进行,需要调整尾门使水槽内水面近似平行于床面,为此布置5个水深测量断面,分别距水槽进口5.0、6.5、7.5、8.5和10.5 m,见图2(b)。各断面都安装有水位测针,其零刻度线与水槽底板齐平,精度为±0.1 mm。在冰盖宽度和流量固定时,通过调整尾门高度,使各断面的水深相等。为确保水流充分发展和避免尾门的影响,流速测量断面为水槽中段的C-C断面,结合断面的对称性,仅测量半宽的断面。自水槽右边壁起,每间隔5 cm布置1条测线,共布置8条测线,依次记为Y05、Y10、Y15、Y20、Y25、Y30、Y35和Y40,每条垂线上均布置10个测点,见图3。对于部分冰封工况,均布置1条测线与冰盖边缘垂线重合。采用标准Vectrion测量各测点的瞬时流速,采样频率设为25 Hz,采样时间不少于60 s,即每个测点至少采样1 500次。根据输出数据的振幅数、信噪比和相关数,对采样的瞬时流速数据点进行质量控制[18],符合要求的用于计算时均流速与脉动流速,进而计算得到雷诺应力和紊动强度,用于揭示冰盖对水流紊动特性的影响。

图3 C-C测量断面上测点布置示意Fig.3 Sketch of measuring points on the C-C measuring section
2 结果与分析
2.1 纵向时均流速分布
时均流速计算公式如下:
(1)
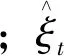
式(1)表明时均流速受采样时间的影响。以B20工况Y20测线上靠近冰盖的测点为例,其纵向时均流速与采样时间的关系见图4,其中u′、v′、w′表示x、y、z方向的脉动流速,为瞬时流速与时均流速之差。

图4 采样时间对时均流速的影响及其脉动流速分布Fig.4 Influence of sampling time on time average velocity and its fluctuating velocity distribution
由图4可见,当采样时间较短时,纵向时均流速波动较大;当采样时间为30 s时,纵向时均流速趋于稳定值,因此,试验确定采样时间为60 s是合理的。同时,横向、垂向时均流速均不等于0,这表明水流除纵向的主流动外,存在叠加于主流之上的二次流;横向时均流速小于0,表明该点的流量总体上是从明流区流向冰盖区;垂向时均流速大于0,表明该点流量总体上是流向无滑移边界的。在脉动流速分布上,3个方向的瞬时流速在时均流速附近波动,脉动流速均满足正态分布。
常用于描述冰盖下纵向时均流速的分布律有双对数律和双幂律。双对数律存在最大流速处不连续、当量粗糙高度不易获取、紊流核心区垂向流速分布不符合双对数律[19]等问题,而双幂律能描述冰盖下水流垂向流速光滑连续的特性,与实测资料也较吻合[12,20],故采用双幂律描述连续冰盖下水流纵向时均流速的垂向分布:
(2)
式中:k0为常数;mb、mi分别为与床面、冰盖粗糙度有关的幂指数。特别地,当mi→∞时,k0→umax,umax为最大流速。式(2)简化为常用于描述明流纵向时均流速垂向分布的单幂律。采用平均百分比误差和拟合度指标评价双幂律的模拟性能,其中平均百分比误差(EMAP)为相对误差绝对值的算术平均值,计算公式为
(3)
式中:i表示数据点数;n为数据量;Y为模型预报值;X为实测值。EMAP最小值为0,其值越小说明模型模拟值越接近参考数据。拟合度指标是常用于判定非线性回归方程拟合度的统计参数,有别于线性回归的确定系数,故记为IFO,其计算公式为
(4)
式中:IFO最大值为1,其值越接近1,说明模型预报值与参考值的吻合程度越好。对于明流O00工况,各垂线的EMAP(u)均小于5.0%,IFO(u)均大于0.90,这表明明流工况纵向流速的垂向分布符合指数律,见图5(a)。该工况的宽深比为4.17,受二次流影响最大流速点偏离自由水面[21],特别是靠近边壁的Y05测线。

图5 O00工况和C40工况纵向时均流速垂向分布Fig.5 Vertical profiles of streamwise velocity for Run O00 and Run C40
完全冰封C40工况的实测流速与式(2)计算值进行对比见图5(b)。当mb=9.69、mi=7.99时,各条垂线的EMAP(u)均小于5.0%,IFO(u)均大于0.90,这表明双幂律可用于描述连续冰盖下水流纵向时均流速的垂向分布。受冰盖附加无滑移边界的影响,各垂线最大流速点位置不同于明流工况,位于垂线中部区域。理论上,最大流速点的速度梯度为0,故将双幂律对z求导,令导数为0得到最大流速点的相对水深为
(5)

部分冰盖形成导致冰盖区上边界为无滑移边界,明流区上边界为自由水面,水流结构较明流工况和完全冰封工况都复杂[15]。目前,针对部分冰盖下水流流速垂向分布的理论分析较少。图6给出B10、B15、B20和B30工况各垂线上的纵向时均流速的垂向分布。由图6可见,部分冰封工况纵向时均流速垂向分布兼具明流和完全冰封工况的特征:① 在冰盖区,所有垂线均类似于完全冰封工况,采用C40工况mi和mb的值,由式(2)得到冰盖区纵向时均流速的计算值,并同实测值对比,结果表明除B20工况Y15垂线外,各垂线的EMAP(u)均小于5.0%,IFO(u)均大于0.90,表明部分冰盖下水流冰盖区纵向流速分布可采用双幂律描述;② 明流区部分垂线类似于明流工况,采用明流O00工况幂指数mb的值,由式(2)得到明流区部分垂线纵向流速垂向分布,各垂线EMAP(u)均小于5.0%,IFO(u)均大于0.90,表明部分冰盖下水流明流区靠近紊流核心区的流速垂向分布符合单幂律;③ 在两者间存在过渡区,纵向时均流速垂向分布既不同于明流工况,也不同于完全冰封工况。根据实测值按双幂律进行拟合,得到的mb均小于C40工况的值,但相反地mi均大于C40工况的值。

图6 部分冰封工况纵向时均流速垂向分布Fig.6 Vertical profiles of streamwise velocity in open channels with partial ice cover
2.2 雷诺应力垂向分布
联立连续性方程和动量方程,得到恒定均匀流的控制方程为[23]
(6)
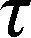
(7)
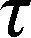
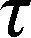
(8)
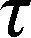
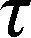
(9)
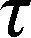
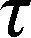
(10)
(11)
式中:u*为断面摩阻流速,这表明紊流核心区雷诺应力在水深方向上呈线性分布。图7(a)对比了明流O00工况Y40垂线上雷诺应力实测值和计算值,结果表明,明流工况紊流核心区的雷诺应力在水深方向上呈线性分布,雷诺应力的最大值出现在床面附近。但是,对应于最大流速点因二次流影响偏离自由水面,雷诺应力零值点也偏离自由水面。
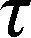
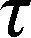
(12)
采用断面摩阻流速对切应力进行量纲一化。采用试验测量的断面尺寸和比降,通过下列公式计算得到u*:
(13)
(14)
式中:hb为床面层的水深;c1、c2为回归系数。显然,切应力零值点相对水深不同于最大流速点,两者相对位置与床面、冰盖的相对粗糙程度有关。以C40工况为例,由式(14)计算的切应力零值点相对水深为0.399,位于最大流速点和相对光滑的固壁之间。

图7 O00工况和C40工况雷诺应力垂向分布Fig.7 Vertical profiles of shear stress for Run O00 and Run C40
对于部分冰封工况,由于冰盖区、明流区的垂向流速分布差异较大,存在横向动量交换,由式(7)推求雷诺应力时不能忽略二次流的影响。目前尚未建立雷诺应力的数学模型,仅能从测量数据探究其垂向分布规律。以部分冰封B20、B30工况为例,冰盖边缘垂线上雷诺应力分布见图8。受横向动量交换影响,雷诺应力在水深方向上散乱分布,不满足线性分布的规律。

图8 部分冰封工况雷诺应力垂向分布Fig.8 Vertical profiles of shear stress in open channels with partial ice cover
2.3 紊动强度垂向分布
紊动强度是流场内任一空间点脉动流速的二阶中心矩,表示瞬时流速在其均值附近的分散程度,反映水体流速脉动的强弱程度。对于明流工况,Nezu等[25]采用指数律描述其纵向紊动强度垂向分布:
(15)
式中:urms为纵向紊动强度;Du和ξu为经验系数。根据明流O00工况实测的瞬时流速,计算得到各垂线的纵向紊动强度,见图9(a)。从紊动强度垂向分布来看,在床面附近存在最大值,随水深增加逐渐减小。当相对水深z/H>0.5后,紊动强度总体上趋于稳定,在自由水面附近达到最小。由图9(a)可见,明流O00工况,各垂线紊动强度垂向分布符合指数律,EMAP(urms)均值为9.43%,IFO(urms)均值为0.895 6。从横向分布来看,总体上越靠近边壁,紊动强度越大,越靠近紊流核心区,紊动强度越小。结合纵向流速的垂向分布,紊动强度在最大流速附近达到最小值,说明最大流速处流速脉动较小,相邻流层间的动量交换最弱。
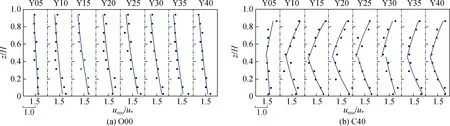
图9 O00工况和C40工况紊动强度垂向分布Fig.9 Vertical profiles of turbulence intensity for Run O00 and Run C40
对于完全冰封工况,按照双层假定将过流断面在垂向上划分为床面层和冰盖层,在各流层中紊动强度垂向分布均符合指数律[26],则
(16)
式中:Du,b、Du,i、ξu,b和ξu,i为经验系数。根据C40工况实测的瞬时流速,计算得到各垂线的紊动强度,见图9(b)。在垂向上,紊动强度在床面和冰盖附近存在最大值,随着到无滑移边界距离的增加而逐渐减小,在最大流速附近达到最小值。经回归分析,C40工况各垂线上床面层和冰盖层的纵向紊动强度均满足指数分布的规律,EMAP(urms)=6.94%,IFO(urms)=0.920 3。
对于部分冰封工况,目前尚未提出描述其紊动强度的分布律,仅能通过分析试验测量数据探究其垂向分布规律。图10给出了B10、B15、B20和B30工况各测线上紊动强度垂向分布,总体上无滑移边界(床面、冰盖)附近的紊动强度相对较大,且边界相对粗糙的冰盖区紊动强度大于边界相对光滑的床面区。部分冰封4种工况冰盖区urms/u*均值分别为1.68、1.87、1.90和1.79,明流区urms/u*均值分别为1.41、1.66、1.78和1.62,冰盖区紊动强度大于明流区紊动强度。当F≤0.5时,冰盖区、明流区urms/u*均随F的增加而增大;当F>0.5时,相比B20工况,B30工况冰盖区、明流区urms/u*均减小,紊动强度减弱。
3 结 论
在普通实验室循环水槽系统中开展模型试验,采用三维声学多普勒测速仪测量不同冰盖覆盖度下恒定均匀流场,从纵向流速、雷诺应力和紊动强度等方面分析冰盖下水流紊动特性,主要得到以下结论:

(2) 明流工况雷诺应力在水深方向上符合线性分布,最大值出现在床面附近;完全冰封工况雷诺应力在水深方向也符合线性分布,切应力零值点位于最大流速点和相对光滑边界之间;部分冰封工况受横向动量交换的影响,雷诺应力在水深方向上不符合线性分布。
(3) 明流工况紊动强度垂向分布符合指数律,完全冰封工况基于双层假定划分的冰盖层和床面层中紊动强度可分别采用指数律描述,部分冰封工况紊动强度受冰盖影响在横向上存在明显的差异。

