黄河三门峡水库水沙电耦合模型研究及应用

夏军强，张贤梓依，王增辉，周美蓉，娄书建

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；3.黄河水利委员会三门峡水利枢纽管理局，河南 三门峡 472000)

水库是调节径流、开发利用水资源的重要工程[1]，多沙河流水库还需妥善处理泥沙淤积问题。世界银行曾指出“将有限的水库库容转化为可持续资源是21世纪水利工程需要关注的重点”[2]。黄河上的水库由于流域多沙的特点，淤积量和淤积速率均居各流域之首[3]，同时黄河流域7座大中型水库均承担发电及供水任务，在区域经济发展、民生保障方面具有重要作用。但蓄水兴利与泄水排沙之间具有典型的博弈关系[4]。因此，如何实现多沙河流水库短期兴利效益和长期减淤效益的平衡具有重要研究意义。

水库调度模型分为模拟模型和优化模型。水库优化模型实质上属于数学规划问题，其基本思想是利用优化算法计算一组决策变量的值从而在各类约束条件下自动寻求目标函数的最优解[5]。自该方面的研究开展以来，优化算法的改进一直是研究热点。其中，以线性规划(LP)、非线性规划(NLP)、动态规划(DP)等为代表的传统算法发展较早且运用广泛，随后遗传算法(GA)、遗传规划(GP)等进化算法(EAs)伴随人工智能的兴起逐渐发展，群体智能(EA-SI)和元启发式算法(MHA)则是该领域内的最新进展[6]。应用不同算法优化水库下泄流量过程以满足灌溉、发电、生态等需求的模型大量发展，但较少有模型进一步考虑水库自身库容的可持续利用[7]。水库模拟模型的功能限于在用户给定的变量下预测水库的运行情况[5]。给定进出口边界时，水库水沙动力学模型能够精确地模拟库区冲淤过程，已有水沙动力学模型不断拓展对库区特殊水沙现象的模拟，如河槽横向冲刷、水库异重流、溯源冲刷及干支流倒灌等[8-11]，使模拟结果不断接近真实的水沙演进过程。尽管优化模型和模拟模型是2种具有不同特征的建模方法，但实际上二者区别并不明显，且在许多模型中互为补充[5]，构成了模拟-优化模型[12-13]。在这类模拟-优化模型中，一些研究虽关注到了多沙河流水库兴利和排沙的矛盾关系，但计算水库冲淤时仅采用经验排沙比公式[7，14]，对这些模型而言，要实现更精细的计算需要与水沙动力学模型结合[15]。另一类模型耦合了水沙动力学模型计算库区冲淤，如彭杨等[16]采用了一维恒定非均匀沙不平衡输沙模型；杨露等[17]采用了准二维非恒定非均匀沙不平衡输沙模型。但这类模型的坝前水位均人为给定，并非模型自动计算所得。综上所述，目前能够自动给定边界条件，并耦合库区水沙演进和发电模拟的水库调度模型较少。

国内学者针对三门峡水库的泥沙问题已构建了许多水库调度模型，其中，Hu等[18]利用一维恒定不平衡输沙模型对库区总冲淤量和潼关高程变化进行模拟，但无法计算出精确的出库含沙量过程；窦身堂等[19]构建的水库高含沙洪水数学模型还包括了对溯源冲刷和异重流现象进行识别和计算的模块，在模拟三门峡水库的出库含沙量过程时与实测值吻合较好。但以上模型并不能在事先给定的调度规则下自动模拟出三门峡水库的调度过程。

本文针对三门峡水库的淤积和发电问题提出水沙电耦合模型。通过实测资料对模型进行率定及验证；结合水库调度模块，定量计算不同水沙条件与调度方案下的冲淤量和发电量；最后利用反映水库综合效益的经济评价指标展开方案比选。模型计算结果可为改善三门峡水库调度方案提供依据及建议。

1 水库水沙电耦合模型的建立

1.1 水库一维水沙计算模块

水沙计算模块采用守恒形式的一维浑水明流水沙耦合控制方程组[10]，形式如下：

(1)

式(1)采用Godunov型有限体积法进行显式离散，形式为

(2)

式中：Um，j、Sm，j分别为第j时间步内第m个控制体内U、S的平均值； Δt、Δx分别为时间步长和空间步长；Fm+1/2，j为第m、m+1个控制体交界面上的数值通量。法向通量Fm+1/2，j的计算是有限体积法的核心，本模型采用HLLC近似黎曼求解器计算[20]。为使方程组封闭，补充床沙上扬通量和悬沙沉降通量计算公式：

Ek=αkωkC*k，Dk=αkωkCk

(3)

式中：ωk为悬沙浑水沉速，m/s；αk为恢复饱和系数，模型中采用韦直林提出的计算方法[21]，即对不同粒径组采用不同的αk值，其与沉速的关系为αk=a/(ωk)b，a一般取0.001，淤积时b=0.3，冲刷时b=0.7，a、b值一般根据实际资料率定得到；C*k为挟沙力，采用张红武等[22]公式计算。

1.2 水库调度模块

水库调度模块主要实现调度模式的自动判断和水量平衡计算两方面的功能。其中，水库调度模式的判断需结合调度规则参数表，目前系统支持进出库平衡、恒定下泄流量、保障下游及敞泄等调度模式[23]。在用户给定的调度规则下，调度模块可自动计算出坝前水位和下泄流量过程。第j时间步内水库调度按照以下流程计算：

(1) 当上一时段采用等流量下泄模式或敞泄模式，此时需判断该时段初库水位(Zj-1)是否达到目标水位。若未达到，则沿用上一时段的调度规则，并令该时段的出库流量(Qout，j)等于上一时段的出库流量(Qout，j-1)， 直接进入步骤(4)；若已达到，则需重新判断该时段的调度规则，进入步骤(2)。

(2) 搜索水库调度规则参数表，确定该时段初库水位所在的水位区间并记录。

(3) 每个水位区间下又划分了若干条子规则。搜索子规则参数表，确定当前时刻(t)和入库流量(Qin，j)下的调度模式(OP)、出库流量以及目标水位(Ztarg)。

(4) 已知出库流量和时段初水位，根据水量平衡原理计算得到时段末水位(Zj)。

图1 水库调度模块计算流程示意Fig.1 Flow chart of the reservoir operation module

1.3 发电计算模块

发电模块采用水轮机出力公式计算发电量。时段j内所有机组的总发电量为

(4)

式中：Ei，j为时段j内第i台机组的发电量，kW·h；Ni，j为时段j内第i台机组的出力，kW；ηi，j为时段j内第i台机组的综合效率系数，根据水轮机运转特性曲线得到；Qi，j为时段j内第i台机组发电引用流量，m3/s；Hj为时段j内全部机组净水头，m，Hj=Zj-Zd-Δh，Zj为时段j内的坝前水位，Zd为下游尾水位，Δh为水头损失；M为机组总数，台。

在计算发电量时，要根据水轮机组本身的参数和水库调度规则，同时满足以下约束：

(1) 发电水头约束。为保证水轮机安全、稳定运行，发电净水头应在一定范围内，应满足：

Hi，min≤Hj≤Hi，max

(5)

式中：Hi，min、Hi，max分别为第i台机组的最低水头和最高水头，m。

(2) 发电引用流量约束。水轮机发电引用流量大小应不超过其最大引水流量，同时所有机组的总过机流量不得超过水库下泄流量，应满足:

0≤Qi，j≤Qi，max

(6)

(7)

式中：Qi，max为第i台机组的最大引用流量，根据水头—引用流量关系曲线插值求得，m3/s；Qout，j为水库下泄流量，m3/s。

(3) 效率系数约束。根据水轮机运转特性曲线可知，水轮机效率系数与发电水头有关，在一定范围内变化，应满足:

ηi，min≤ηi，j≤ηi，max

(8)

式中：ηi，min、ηi，max分别为第i台水轮机的最小效率系数和最大效率系数。

(4) 出力约束。各台机组的实际出力不得超过限制出力，应满足:

0≤Ni，j≤Ni，j，max

(9)

式中：Ni，j，max为第j时段内第i台水轮机的限制出力，根据水头—出力限制曲线插值求得，kW。

(5) 水位约束。各机组发电水位对应水库的年内调度过程，应满足:

非汛期：Zi，min≤Zj≤ZNF

(10)

汛 期：Zi，min≤Zj≤ZFL

(11)

式中：Zi，min为第i台机组的最低运行水位，m；ZNF为非汛期正常蓄水位，对于三门峡水库取318.0 m；ZFL为汛期汛限水位，对于三门峡水库取305.0 m。

1.4 模型计算步骤

模型计算时按照数据输入—水库调度—发电量计算—水沙计算—河床变形计算—床沙级配调整等步骤进行。输入输出模块首先读入事先准备的断面地形、进口水沙、沿程床沙以及调度规则资料；在第j时间步内，调度模块自动计算出坝前水位和下泄流量过程，为发电模块提供计算条件进而求出时段内发电量；同时调度模块为水沙模块提供下边界条件，从而计算出式(1)中各断面水沙要素Am，j、Qm，j、Cm，j、A0m，j，得到沿程流量、含沙量及水位。

2 水沙电耦合模型的率定及验证

三门峡水库是黄河干流上兴建的第一座以防洪为主的综合性水利枢纽，水库在蓄水运用初期库区发生严重淤积。为提高泄流排沙能力，水库经历了2次大规模改建和2次运用方式调整。2003年至今，三门峡水库在蓄清排浑运用的基础上采用“318运用”方案。三门峡电站第一台低水头发电机组于1973年投运，经历了全年发电、汛期停发、浑水发电试验及汛期发电原型试验4个阶段[24]，目前水电站拥有7台发电机组，总装机容量达460 MW，表1给出了三门峡电站发电机组基本参数。在计算发电量时，由于三门峡枢纽整体下泄流量不大，下游尾水位视作固定值278 m，水流通过水轮机造成的水头损失取1 m[25]。

表1 三门峡水电站1—7号发电机组参数

三门峡库区潼关—三门峡坝址河段(简称潼三河段)全长112.5 km，流域面积为6 257 km2，为陕、晋、豫三省界河。水库蓄水运用后，潼三河段受上游来水来沙和下游水库运用方式的协同作用，自上游至下游河道自然属性减少，受水库影响渐强[26]。河段内布设潼关站和三门峡站2个水文站，沿程设置古夺、大禹渡等若干水位站以及33个淤积观测断面，如图2所示。

2.1 模型率定

模型研究范围为潼三河段，计算采用该河段2018年10月末实测33个淤积断面形态作为初始地形，并对各断面进行滩槽划分。沿程各断面的初始床沙级配根据2018年汛后已知断面床沙级配插值得到。由于初始地形及床沙级配采用10月的实测资料，故模拟时段为2018年11月1日至2019年10月31日，共计8 760 h。该水文年入库水量为411亿m3，沙量为1.72亿t，为丰水枯沙年。计算时水沙资料均采用日均值，图3给出了进出口边界的水沙过程。

图2 三门峡库区示意Fig.2 Plan view of the Sanmenxia Reservoir

图3 模型率定计算的水沙边界条件Fig.3 Boundary conditions used in the model calibration

图4给出了2019水文年出库日均流量过程的计算值与三门峡站实测值的对比情况，以及沿程3站(潼关、古夺、北村)水位计算值与实测值的对比情况。由图4可见，流量计算结果与实测值较为符合，均方根误差(ERMS)为219 m3/s，远小于平均流量1 286 m3/s，纳什效率系数(ENS)达0.92。实测最大流量为5 005 m3/s，计算最大流量为4 270 m3/s，两者相对误差为17%。由图4(b)—图4(d)可以看出，计算与实测的水位过程符合良好，沿程3站水位计算值和实测值的ERMS为0.12～0.61 m，ENS为0.83～0.96，最高水位的绝对误差(|ΔZmax|)为0.05～0.14 m，远小于各站的实际水位变幅(2～10 m)。

图5(a)给出了2019水文年日均出库含沙量计算值与三门峡站实测值的对比情况。由图可知，计算含沙量过程与实际过程的变化趋势吻合。对应三门峡水库汛期的2次敞泄，实际三门峡站出现2次沙峰。第1次敞泄期间实测最大含沙量为143 kg/m3，计算最大含沙量为48 kg/m3，远小于实测含沙量。第2次计算出的2次沙峰的含沙量分别为32.8 kg/m3、19.8 kg/m3，实测含沙量分别为32.5 kg/m3、46.7 kg/m3，相对误差分别为1%、58%，可见模型计算小沙峰时精度较高，但在模拟敞泄期间高含沙水流时计算精度还存在提升空间。基于输沙量法得到的全年实际泥沙冲刷量为1.078亿t，模型计算值为0.734亿t，较实测值偏小32%。

图5(b)为计算与实测发电量的对比图。可以看出，发电量计算值与实际值符合较好，能基本模拟出实际发电过程。ERMS值为117万kW·h，ENS值达0.72。统计该年全年、非汛期及汛期发电量的计算值和实际值，计算值分别为20.85亿、15.33亿及5.52亿kW·h，较实际值分别偏小1%、偏小5.4%以及偏大13.5%。分析误差来源于计算发电时未考虑调峰需求、机组检修、汛期临时停机避沙等特殊情况。

图4 2019水文年流量及沿程水位的计算值与实测值对比Fig.4 Comparisons between calculated and measured hydrographs of discharge and water levels along the reach in the 2019 hydrological year

图5 2019水文年含沙量及发电量计算值与实测值对比Fig.5 Comparisons between calculated and measured hydrographs of sediment concentration and power output in the 2019 hydrological year

2.2 模型验证

模型验证计算时段为2019年11月1日至2020年10月31日，初始地形采用2019年10月末实测断面形态。该年水沙过程及水库运用过程与率定年份类似，但水沙年内分配更不均匀，汛期来水、来沙分别占全年的61%和91%。进出口边界条件设置与率定计算时类似，流量糙率关系、挟沙力公式参数以及恢复饱和系数均采用率定结果。

图6分别给出了2020水文年计算日均出库流量与三门峡站实测值的对比情况，以及沿程3个水位站的水位计算值与实测值的对比情况。由图6可以看出，流量的计算结果与实测值大体符合，ENS值达0.97。实测最大日均流量为5 750 m3/s，对应该日计算值为5 937 m3/s，误差为3%，但在7月份的敞泄期偏差稍大。水位计算值的ERMS值为0.19～0.48 m，远小于各站实际平均水位，ENS值为0.29～0.97， |ΔZmax|不超过0.7 m，但部分时段在大禹渡断面水位误差较大，表明计算与实测的水位过程大致相符。

图7给出了2020水文年出库含沙量及发电量计算值与实测值的对比情况。由图7可以看出，计算出库含沙量过程与实际过程总体符合，但在模拟敞泄冲刷前期淤积泥沙出库时存在较大误差。第1次敞泄的计算含沙量远小于实测值(147kg/m3)，第2次敞泄计算最大含沙量为42 kg/m3，与实测值(47 kg/m3)误差为10%，计算精度较高。此外，计算的发电量与实际值总体符合良好，统计出全年、非汛期以及汛期发电量计算值分别为24.40亿、17.24亿和7.15亿kW·h，较实际值相对误差分别为14.6%、3.5%及11.2%。经模型率定及验证，该模型能够较为准确地模拟库区水沙演进过程及电站发电过程，可进一步对不同水沙过程和水库调度方案开展数值模拟研究。

图6 2020水文年流量及沿程水位计算值与实测值对比Fig.6 Comparisons between calculated and measured hydrographs of discharge and water levels along the reach in the 2020 hydrological year

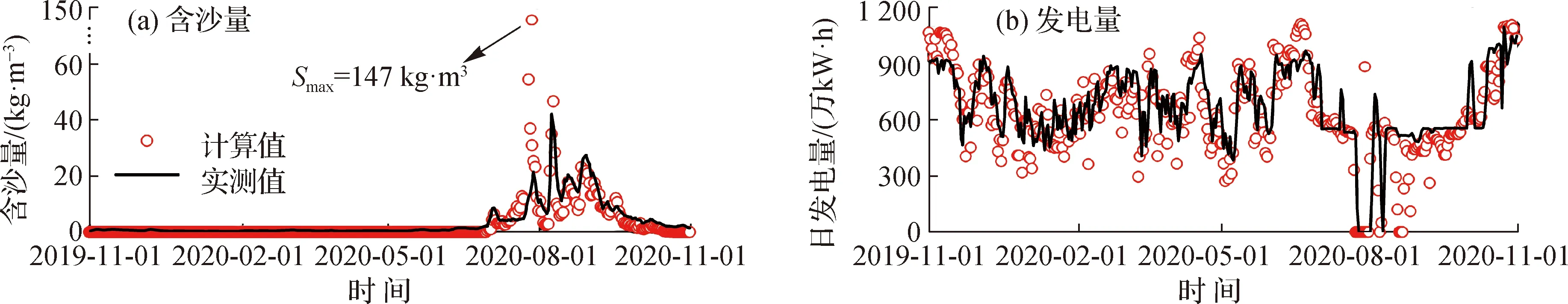
图7 2020水文年含沙量及发电量计算值与实测值对比Fig.7 Comparisons between calculated and measured hydrographs of sediment concentration and power output in the 2020 hydrological year

3 不同水沙条件与调度方式对库区冲淤及发电的影响

利用水库调度模块，输入三门峡水库调度规则，可自动计算出库流量过程和坝前水位过程。为研究模型对于入库水沙条件的响应特点并为改善水库运用方式提供参考，现设定不同水沙条件和调度方式作为模型输入。

3.1 不同水沙条件对水库冲淤及发电的影响

采用典型年实际水沙过程设定不同入库水沙条件，以分析三门峡库区冲淤量和电站发电量受不同水沙条件影响的规律。

3.1.1 水沙典型年选择

利用1991—2020年潼关站的系列水沙资料，采用坐标图方法选取水沙典型年[27]。最终选择1993年为丰水丰沙典型年，1997年为枯水丰沙典型年，2004年为枯水枯沙典型年，2019年为丰水枯沙典型年。在4种来水来沙条件下的计算均采用2019年汛末地形、床沙级配、悬沙级配等数据，并统一采用现状调度规则，重点研究不同入库水沙条件对库区冲淤及电站发电的影响。

3.1.2 计算结果及分析

(1) 发电量、淤积量对比及分析。图8(a)和图8(b)给出了4种典型水沙过程下的计算坝前水位过程、发电量和冲淤量。可见不同水沙条件会造成冲淤量和发电量的巨大差异，丰水枯沙过程下库区发生冲刷，冲刷量为0.3亿3，发电量为23.0亿kW·h，其余丰水丰沙过程、枯水丰沙过程以及枯水枯沙过程下库区均发生淤积，淤积量较丰水枯沙过程分别增加了317%、360%以及129%，发电量较丰水枯沙过程分别减少了18%、52%以及35%。采用能够反映水沙搭配关系的来沙系数以及和发电密切相关的流量分析其与冲淤量和发电量的关系，由图8(c)和图8(d)可知，发电量和水量之间呈良好的正相关关系，库区累计冲淤量与来沙系数变化趋势一致。

(2) 机组投入使用情况分析。图9和图10分别给出了1—5号单机、6—7号单机在4种典型来水来沙过程下的实际出力线和出力限制线。可以看出，由于各年水量不同，实际出力线包围面积占限制出力线包围总面积的比例随之变化：水量越大，实际出力线包围面积占比越大。这代表实际出力随水量增长而增加，而潜在发电能力随之减小。统计1—5号机组及6—7号机组的满发天数占比，可得：在丰水枯沙条件下，1—5号机组43.8%时间处于满发状态，在枯水丰沙条件下仅有3.6%的时间处于满发状态；在各种水沙条件下6—7号机组满发天数占比均小于2.2%，故存在很大发电潜力。

图9 1—5号单机在典型来水来沙过程下的实际出力线和出力限制线Fig.9 Actual power output curves and limit power output curves for the No.1—No.5 turbines in 4 typical flow-sediment regimes

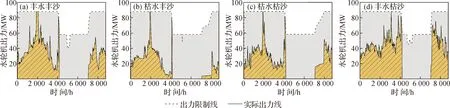
图10 6—7号单机在典型来水来沙过程下的实际出力线和出力限制线Fig.10 Actual power output curves and limit power output curves for the No.6—No.7 turbines in 4 typical flow-sediment regimes

3.2 不同调度方式对水库冲淤及发电的影响

设计不同调度方案，以研究三门峡水库在不同调度方案下的库区排沙效益和电站发电效益，为三门峡水库运用方式的改善提供依据及建议。

3.2.1 调度方式设计

非汛期水库运用的关键指标为非汛期起调水位，汛期水库运用的关键指标有平水发电期水位、敞泄的临界入库流量以及平水发电期时长。在现状运用方式的基础上改变关键指标，设计4种调度方案，分别为：① 工况1，非汛期起调水位由现状方案的318 m降至315 m；② 工况2，汛末回蓄时间延后500 h；③ 工况3，汛期敞泄的临界入库流量由现状方案的2 500 m3/s提高至3 000 m3/s；④ 工况4，汛期平水期发电水位由现状方案的305 m抬高至306 m。上述4种工况的入库水沙过程均采用2019水文年数据，库区地形一律采用2018年汛后地形。

3.2.2 计算结果及分析

(1) 发电量、冲淤量对比及分析。表2给出了现状方案及各工况的发电量及冲淤量。对比工况1与现状方案可以看出，非汛期发电量减幅为5%，但非汛期淤积量减幅高达83%，可见非汛期降低坝前水位可大幅减少库区淤积。对比工况2—工况4与现状方案可以看出，工况2通过延长汛期平水发电时间增加汛期发电量，但非汛期发电时间减少，发电损失更大，故该方式并不推荐。工况3和工况4的年冲刷量分别仅减小0.005亿、0.004亿 m3，但年发电量分别增长了0.51亿、0.17亿kW·h。因此，为获得发电、减淤综合效益，初步推荐增大汛期敞泄的临界入库流量和抬高汛期平水发电水位的方式。

表2 现状方案及各工况的发电量、冲淤量及综合效益值

(2) 基于经济价值量化指标比较。采用夏军强等[28]提出的水库优化调度模型中评价发电、减淤二者综合效益的指标，对三门峡水库排沙减淤和电站发电效益进行经济价值量化。指标形式为

(12)

式中：F为考虑排沙、发电的综合效益评价指标，元；λ1为三门峡水电站上网电价，元/kW·h；λ2为水库单位建设成本，元/m3；Ej为时段j内机组总发电量，kW·h；T为总计算时长，h；ΔV为损失库容，m3。根据文献[29-30]取λ1=0.242，λ2=1.12，表2给出了现状方案及4种设计工况的综合效益指标计算值。可以看出：4种工况效益值接近，其中工况3综合效益值最大，可达5.84亿元，因此，为获得较大的排沙、发电综合效益，可适当提高汛期敞泄的临界入库流量。

4 结 论

本文基于三门峡水库2019水文年和2020水文年实测水沙和发电量资料，通过耦合水库一维水沙计算、水库调度和发电量计算3个模块，建立了水库水沙电耦合计算模型，并对模型进行了率定及验证。研究了不同水沙条件和调度方式对水库冲淤和发电的影响，主要结论如下：

(1) 水库淤积量和电站发电量受入库水沙条件影响大，相较丰水枯沙过程，丰水丰沙过程、枯水丰沙过程及枯水枯沙过程下的库区淤积量分别增加了317%、360%以及129%，发电量分别减少了18%、52%以及35%；电站以水定电，发电量受来水量影响大，淤积量与来沙系数密切相关。

(2) 降低非汛期起调水位有利于控制非汛期库区淤积，利用经济价值指标量化比较后得出，提高汛期敞泄的临界入库流量有利于提高减淤及发电综合效益。