以实证分析促进概念的深度理解——“有余数的除法”的教学重构

□ 张优幼

教师教学行为的改进，要从经验观察走向事实分析，从感性思考走向理性研判。通过实证分析，获得最佳研究证据，能帮助教师理解学生的认知差异，对学材组织、学习方式和评价反馈等作出合理的调整。如何通过实证数据，凸显事实分析，关注过程反馈，以达成概念的深度理解呢？笔者以“有余数的除法”教学为例，进行了如下探索与思考。

一、缘起学生“犹豫不决”的答题

在“有余数的除法”教学后，学生在看图写算式时出现了图1的结果。如图所示，学生写好算式后又进行了修改，先写的是正确的算式“10÷4=2……2”，后改成错误的算式“10÷2=4……2”。这一修改过程能展现出学生答题时的犹豫不决。

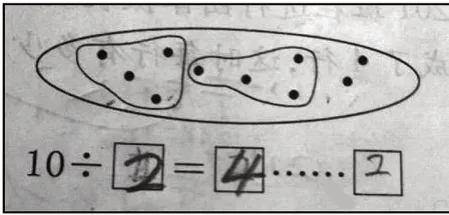
图1

这种“犹豫不决”是缘于学生对“有余数的除法”含义的不理解吗？还是缘于对“等分除”和“包含除”的混淆？或是对“余数要比除数小”这个规律的感知不够深入，从而不能进行迁移应用？为解决这一问题，教师需要分析学生的学习过程。

二、基于学生经验的实证分析

实证分析不是简单地为解决一节课的教学进行数据收集，而是指向学生学习数学的动态发展过程。因此，教师要把一节课的学习内容放在一个教学单元甚至一个学段的知识结构中进行实证，分析学生的学习经验，从而从内容割裂走向教学整合。

（一）明确实证内容的关键

各版本教材通常在二年级下册安排有余数的除法的教学。人教版教材把它安排在了平均分、除法含义和用乘法口诀求商的教学内容之后（如图2）。

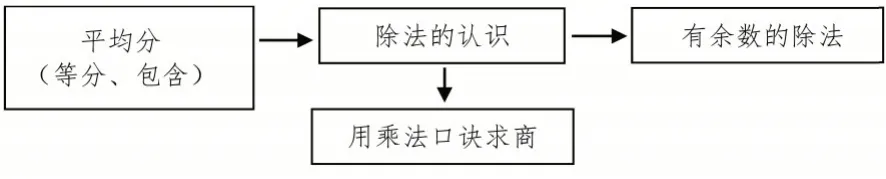
图2

人教版教材在编排“有余数的除法”的含义时，是从“刚好分完”的除法算式迁移到“均分后有剩余”的除法算式的。有余数的除法算式通常由教师借助情境和图式直接告知学生（如图3）。可这样的告知符合学生的认知规律吗？这就需要教师进一步思考以下三个问题。

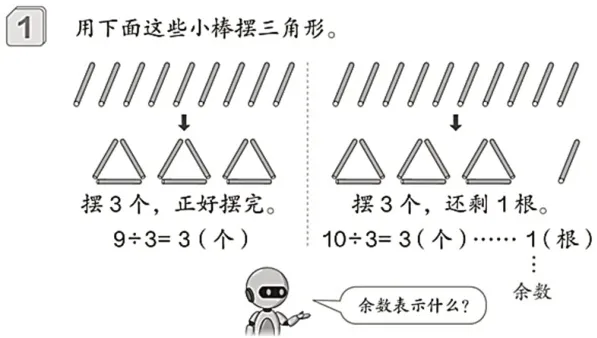
图3

1.平均分的意义需要扩展吗

学生会认可“均分后有剩余”也是平均分吗？从整体上看，建构除法概念需要经历两个不同阶段，即“表内除法”和“有余数的除法”，分别对应“刚好分完”和“均分后有剩余”两种情况。除法的本质是平均分。为了建立“平均分”和“除法”之间的联系，第一阶段的学习重点聚焦于“刚好分完”的情况，从而建立“平均分”与“刚好均分”的强关联。那么，“平均分”与“均分后有剩余”的关联是怎样的呢？对于例题中首次出现的“摆3个，还剩1根”的结果，学生是否会认可这也是平均分，可以用除法表示呢？

2.会用除法算式吗

如果学生认可“均分后有剩余”也是平均分，那么他们会用除法算式表示吗？如果不会，那会用什么算式表示？

3.对除法算式的理解会受影响吗

平均分有两种不同的情况，一种是等分，一种是包含。与之相关的，基于不同的均分过程，除法算式含义可分为“等分除”和“包含除”。那么，在有余数的除法算式中，学生能对其进行辨认吗？

针对这三个问题，笔者用测试和访谈的方式，对城区某校二年级272 名学生进行了课前和课后的实证。

（二）分析实证数据的表现

1.“均分后有剩余”与“平均分”的弱关联

用图4对学生进行课前测试，结果显示，测试中没有学生把题③看作平均分；题②增加了3个圈作为固定份数，只有约5.15%的学生认为是平均分。在访谈中，有学生认为：“第②幅图表示的是有3份，每份同样多，所以也是平均分，剩下的那颗糖就不管了。”

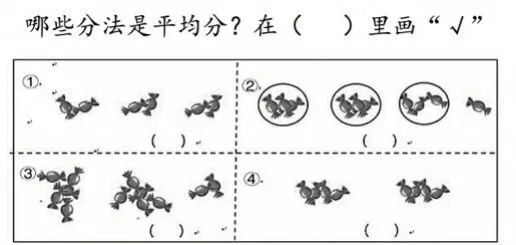
图4

思考：如果学生不认为均分后有剩余是平均分，那么就很难理解用除法算式来表示均分后有剩余。因此，教师要先引导学生认识平均分，再帮助他们进一步理解“有余数的除法”的含义。那为什么有些学生认为题②也是平均分呢？因为固定了份数，就能直观地看到每份同样多。

启示：在教学中，对于静态的图，首先要理清份数，在份数的基础上识别每份都同样多的结果。在动态操作的过程中，则要先确定每份数，再与份数进行关联。教学中，教师要结合动作、图式、语言和算式等进行多元表征。

2.“均分后有剩余”与除法算式的陌生感

教学前，对于“均分后有剩余”的情况，学生能用有余数的除法算式来表示吗？有多少学生已经能迁移应用？如果不用除法算式，学生又会用怎样的算式表示“均分后有剩余”呢？针对这个问题，笔者采用单个情境操作后列算式（如图5）和同个情境不同均分结果操作后列算式（如图6）两种方式对学生进行课前测试。

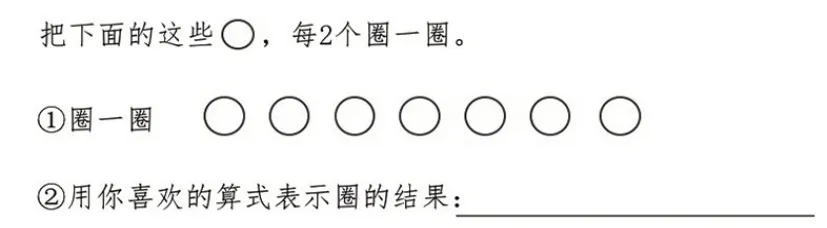
图5

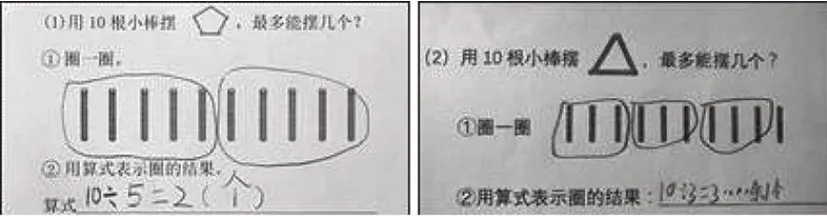
图6

在单个情境操作后列算式的测试中，用连加、乘加算式表示的学生约占12.87%，用连减、乘减算式表示的学生约占69.12%，用除法算式表示的学生约占18.01%。从数据中可以看出，相对于除法算式，学生更喜欢用乘加、乘减的方式表示均分后有剩余的结果，如3×2+1=7、7-2×3=1等。

在同个情境不同均分结果操作后列算式的测试中，学生用除法算式表示的约占39.71%。从数据中可以发现，以对比的方式呈现“刚好分完”和“均分后有剩余”两种情况，用除法算式表示的学生人数显著增加，从18.01%左右上升到了39.71%左右。有意思的是，部分学生虽然不能正确地书写有余数的除法算式，但已经有了用除法算式表示的意识（如图6右图）。然而即便有强暗示的情境对比，大部分学生仍对除法算式感到陌生。

启示：用“刚好分完”和“均分后有剩余”的对比情境导入，让学生感受到为合理清晰地表达均分结果，用除法算式进行表征很有必要；但不能否认学生的原有认知经验，要让学生在多个不同算式的表征中进行比较辨析，进一步理解有余数的除法算式表示的含义。

3.“包含除”与“等分除”对理解除法算式的难易不同

把一些物品按指定的份数进行平均分，可以一个一个地分，也可以几个几个地分，直到分完为止，即等分除；把一些物品按每份个数一份一份地分，即包含除。这两种分法，在理解除法算式的难易度上是否有偏差？针对这个问题，笔者对学生进行了课后测试。

（1）对比一：把分的结果画一画，再填一填，并用算式进行表示。

①9 支铅笔，每人分2 支，可以分给（ ）人，还剩（ ）支；

②9支铅笔平均分给4人，每人分（ ）支，还剩（ ）支。

第一种分法是按每份的个数进行均分，学生能在给定9支铅笔的图上，按每份2个圈一圈，并且列出正确算式；第二种分法给定4 个框，让学生按份数一一等分，在这个过程中，几乎学生没有添画上4个框外那1根剩余的小棒。

（2）对比二：“10÷4=2……2”表示什么？请用画图的方式表示你的想法。

根据有余数的除法算式画图时，学生习惯用“包含除”来理解“均分后有剩余”的结果，而用“等分除”来解释除法算式含义的学生非常少。这说明学生能理解有余数的除法算式的含义，他们的认知表象建立在“包含除”的均分之上。

就有余数的除法概念的认识而言，“等分除”的均分方法确实不像“包含除”那样，能清晰地看到圈后余下的结果。因为“等分除”的操作过程是一一均分，无论是操作还是想象都比较麻烦，且容易受表内乘法口诀的影响，从结果出发而忽略一一均分的过程。然而，从对后续学习的价值来说，等分后有余的均分过程和方法是不可忽视的，如解决抽屉问题时，就是先用一一等分的方法建构抽屉，再将余数装入其中一个抽屉来建立模型的。

启示：要建立完整的有余数的除法的含义，必须感知两种不同分法的均分过程。虽然从“包含除”导入更容易理解，但如果仅关注“包含除”而忽略“等分除”，则会在后续学习中产生认识上的偏差。为此，需要借助观察演示、动手操作、感知对比等方式，感知“等分除”后有剩余的均分过程。

三、探寻基于实证的教学重构

基于实证分析，笔者对“有余数的除法”进行教学重构，在问题的引领下，寻找证据，分析证据，应用证据，从而改进教学（如图7）。

图7

重构后的教学，关注“均分后有剩余”与“平均分”的强关联；从学生已有的知识经验出发，比较不同算式的表示方式与有余数的除法算式之间的联系，将除法的意义从“刚好分完”向“均分后有剩余”扩展；在操作中抽象比较“包含除”与“等分除”，凸显对“等分除”过程中有余数的除法的含义的理解。

（一）在联系比较中明晰概念内涵

对数学概念的理解离不开分析、比较、辨析、归纳等思维活动，学生的思维活动有助于概念的原型建构和变式比较。教师的教学需要在多元表征的基础上，建立“余数”与平均分及除法算式之间的关联，让学生理解“有余数的除法”与除数的关系。

1.有余数的除法算式顺向迁移，在多维生成中比较联系

借助任务一的题组（如图8），让学生在相同的情境中，实现从“刚好分完”到“均分后有剩余”的比较迁移，构建新的认知结构。理解概念时，引导学生从原有的认知基础出发，多向生成，优化有余数的除法算式的表征，初步建立余数概念。教学反馈时，通过两次对比帮助学生完成概念的建构。

图8

（1）第一次对比，比较有余现象的原始表征和有余数的除法算式。教师呈现学生列出的算式：①3+3+3+1=10；②3×3+1=10；③10-3-3-3=1；④10-3×3=1；⑤10-1=9，9÷3=3；⑥10÷3=3……1。让学生对应图说说这些算式分别表示什么意思，并借助这些不同的算式，理解10÷3=3……1表示的含义。学生在比较中明确了乘加、乘减等算式与有余数的除法算式的关联，而优化有余数的除法能清楚地表示圈后有余的结果。

（2）第二次对比，比较图8 中两道题的算式：10÷5=2 和10÷3=3……1。这两道题为什么都可以用除法表示分后的结果？它们有什么相同点和不同点？让学生理解有余数的除法也需要平均分，也可以用除法算式表示，并结合动作、语言和图式等进一步理解除法算式。

学生通过两个不同层次的比较，建立“刚好分完”和“均分后有剩余”两种情况之间的联系，初步认识了有余数的除法含义。

2.规律归纳开放生成，在多向联系中感悟内化

对于二年级学生来说，形式化的告知只能使他们机械识记规律。因此，教师教学时要明确余数与除数的关系，让学生借助任务驱动，助推规律的生成，并在多向联系中比较、归纳、感知规律（如图9）。

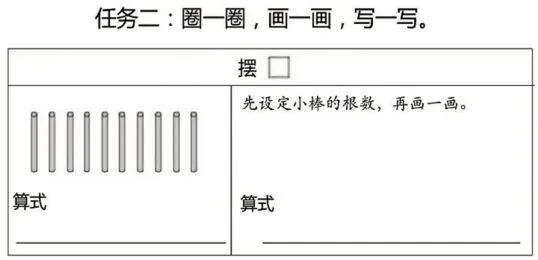
图9

（1）横向对比，感知除数是4 时余数的特点。①用10根小棒摆正方形，巩固有余数的除法算式的含义、读写法等。②自己设定小棒的数量，画一画，用除法算式表示结果，从而得到除数都是4，被除数各不相同的有余数的除法算式。通过不完全归纳比较，理解所有除数是4的除法算式中，不管被除数是几，余数都只有1、2或3（余数是0通常不写）。教师引导学生思考：“有没有画出余数是4或比4大的？”“余数除了1、2和3，还有其他的可能吗？”“如果小棒根数再多一些，余数会发生变化吗？”让学生通过操作演示，理解“余数要比除数小”这一规律。

（2）纵向对比，不仅从摆正方形（除数4）的算式中概括余数比除数小的规律，还可以通过摆五边形和三角形（除数是5 或3），进一步感悟余数和除数的关系。让学生通过对□÷4=□……□、□÷5=□……□、□÷3=□……□三组算式中余数与除数关系的思辨，概括规律。

“余数要比除数小”的规律，不是仅通过按序观察一组算式得到的。要让学生利用开放式的生成资源，自己设定小棒数量进行感悟，从具体到抽象，跳出被除数按序排列的框架，跳出单一除数的限制，用归纳的方式横向对比相同除数的算式，并用不同除数进行纵向对比，在联系和迁移中深度理解概念和规律。

（二）在任务驱动中改进学习方式

基于实证的数学课堂，既要对教师的教学方式进行改进，又要对学生的学习方式进行优化。用问题情境和任务驱动的方式依序推进教学，能激发不同层次学生的探究欲望，使他们在比较和归纳中形成概念。课堂重构后，学生在三次对比任务的驱动下完善对概念的理解。任务驱动的学习材料典型而简约，有结构且具有可操作性。

任务三是在操作中理解“包含除”与“等分除”，重点是有余数的除法中的“等分”过程。

（1）第一次对比平均分19根小棒，比较每5根均分与平均分成5份（如图10）。19根小棒平均分成5份，剩余的4根无法继续一一等分，这就是余数。让学生从中感受“包含除”和“等分除”均分过程的不同，理解一一等分是余数与除数（份数）建立联系。

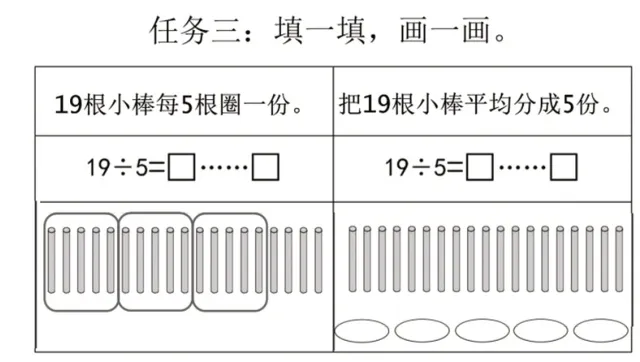
图10

（2）第二次对比平均分19根小棒，比较平均分成5 份与平均分成3 份（如图11）。让学生通过操作进一步感受“等分除”有剩余的过程，理解余数与除数（份数）的关系。“为什么平均分成5份时，余数可以是4，而平均分成3份时，剩余的4根还要继续均分呢？”学生在追问中理解了有余数的除数的本质，明确了除数与余数的关系。

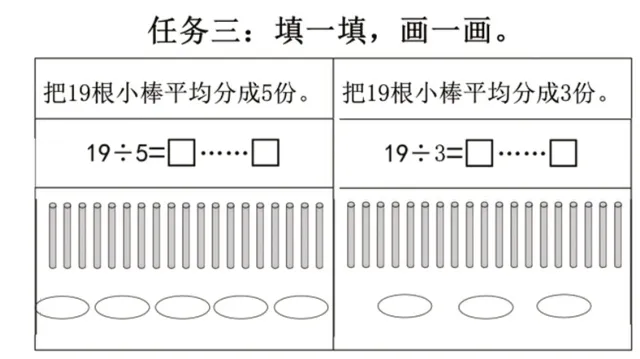
图11

两次对比注重过程和关联，学生经历动作、语言、图式的不同表征过程，完善了对概念的认知。

实证教学，关注的是学生的“学”，指向的是学生的动态发展过程。它关注学生的知识经验，从现状出发剖析成因，从一节课的教学追溯到一个体系的教学。教师要根据有效数据的反馈和分析，实施精准教学，重构课堂，从而促使学生实现对概念的深度理解。