液黏调速器接合过程建模与特性分析

王翔宇, 汪浒江, 郝惠敏, 黄 曦, 黄家海

(1.太原理工大学机械与运载工程学院, 山西太原 030024; 2.中国北方车辆研究所传动系统技术部, 北京 100072; 3.太原理工大学土木工程学院, 山西 太原 030024)

引言

液黏调速离合器的接合过程主要分为流体润滑、混合摩擦、边界摩擦、干摩擦四个阶段,通常是根据油膜厚度h与摩擦盘表面粗糙度σ的比值来判断其工作状态。其中在流体润滑阶段, 两摩擦盘表面完全被

油膜覆盖,微凸体完全分离。在混合摩擦和边界摩擦阶段,两摩擦盘表面的微凸体一部分被油膜覆盖,另一部分微凸体相互接触,此时,离合器的传动扭矩由液黏扭矩与摩擦扭矩组成,随着接合过程的进行,油膜厚度减小,微凸体接触面积越来越大,接合过程逐渐进入干摩擦阶段,此时,不存在油膜挤压,传动扭矩完全由摩擦扭矩组成。本研究主要对前两个阶段进行分析讨论。

目前,大部分研究都是针对车辆和船舶的湿式摩擦离合器,对液黏调速离合器接合特性的研究很少。1978年,PATIR N等[1]首先提出考虑摩擦副综合粗糙度的平均流量模型,并广泛应用于挤压膜流动的研究当中。2019年,刘强等[2]使用PATIR N提出的平均流量模型分析了离合器软启动过程。之后,王成等[3]将平均流量模型应用到湿式离合器当中,分析了离合器的接合过程及其温度场。2021年,BAO H等[4-5]加入了机械振动的因素,对湿式离合器动力学和接合特性等方面做了相关研究。WANG Y等[6]研究了带排转矩对湿式离合器的影响,并综合考虑了径向油槽结构。在求解离合器摩擦副流场特性时,很难得到雷诺方程的解析解,通常用数值方法来求解。1996年,BERGER E J等[7]开发了一种有限元模型,模拟了考虑粗糙度的可渗透湿式离合器的接合,通过雷诺方程探讨了活塞压力对转矩的影响。2019年,纪敬虎等[8]采用多重网格法对雷诺方程进行数值求解,探究了粗糙度对交叉沟槽织构化表面流体动力润滑性能的影响。2021年,黄伟等[9]在BERGER E J的基础上,采用了有限差分法求解雷诺方程,对离合器的挤压特性进行了仿真分析。由于液黏传动中流体惯性项对动态传动特性会产生影响,因此,在1980年,VORA K H等[10]发现流体惯性的影响会降低负载能力。相反,SINGH P[11]导出了一个包含惯性效应的解析解。他发现,随着雷诺数的增加,流体膜的承载力增加。GETHIN D T[12]开发了一个数值模型,由于该模型忽略了控制方程中的惯性项,仿真结果的薄膜间隙衰减速率比实验结果的衰减速率稍快。在2011年,黄家海[13]建立了考虑离心力在内的离合器动力学模型,通过迭代求解获得了离心力、接合压力等因素对摩擦副动力学特性影响规律。2015年,崔建中[14]推导出考虑惯性项和不考虑惯性项的离合器软启动数学模型,通过Fluent分析了不同工况条件下对离合器动力传递的影响。2018年,宫华胜[15]推导出考虑科氏力的液黏离合器数学模型,通过FORTRAN软件分析了不同工况条件下对离合器动力传递的影响。此外,关于摩擦副表面的粗糙度接触也有学者进行了大量研究。1966年,GREENWOOD J A等[16]提出了Greenwood Williamson (GW)接触模型,并得到了广泛应用。2021年,楼振雄等[17]采用库伦摩擦模型分析了湿式离合器的转矩响应,认为其无法体现滞后性。之后,陈剑等[18]和周华等[19]从一些基础粗糙模型衍生出改进模型,并提到了分形理论的影响。

综上可知,目前对挤压膜流动以及粗糙表面间润滑已有大量研究,但对考虑表面粗糙度的液黏调速离合器接合特性研究较少,而且通常都将摩擦副简化为粗糙平面,忽略了油槽结构。本研究综合考虑摩擦片油槽结构的影响,对液黏调速离合器流体润滑和混合摩擦阶段的转速转矩等动力学参数建模。采用有限体积法对二维雷诺方程求解,结合GW粗糙模型得到离合器的接合特性。

1 液黏调速离合器数学模型

1.1 动压承载模型

如图1所示,是液黏调速离合器简化模型。

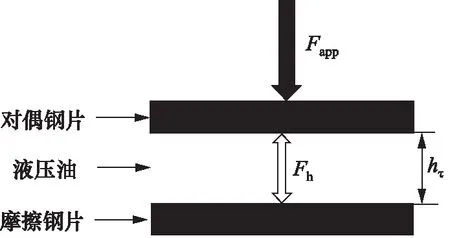
图1 液黏调速离合器简化模型

图1中,Fapp为接合压力,N;Fh为油膜动压承载力,N;hτ为名义油膜厚度,m。

针对液黏调速离合器的纯油膜和混合摩擦两种摩擦工作状态,考虑表面粗糙度以及油槽结构等因素对摩擦片间油膜厚度的影响,基于Patir和Cheng平均流量模型,引入压力流量因子,建立考虑流体惯性项、表面粗糙度以及油槽影响的等效瞬态雷诺方程如式(1)所示:

(1)

式中, φr, φθ—— 径向流量因数和周向流量因数,

φr=φθ=1-exp(-0.56h/σ)

h —— 油膜厚度,m

ρ —— 润滑油密度,kg/m3

ω1,ω —— 主动盘转速和摩擦副的相对转速,rad/s

通过式(1)可以得到摩擦片间的动压分布ph,并在整个摩擦区域上进行积分可以得到摩擦片间的油膜承载力Fh:

1.2 微凸体接触承载模型

随着油膜厚度在控制压力的作用下逐渐变薄,粗糙峰开始接触。根据Greenwood所提出的粗糙峰接触理论以及Patir得出的粗糙峰接触承载力与油膜厚度比之间的近似关系,粗糙面峰的单位接触压力表示为:

(3)

其中,λ是油膜厚度比,表示名义油膜厚度h与综合粗糙度均方根σ的比值, K′和E表示如下:

式中, Ei—— 摩擦副弹性模量,i=1,2

vi—— 泊松系数,i=1,2

因此粗糙峰接触承载力可以在摩擦副全域上进行积分并表示如下:

用γ来表示微凸体的接触面积与标称接触面积比值,则接合过程中总承载力可表示如下:

Fapp=γFc+(1-γ)Fh

(6)

γ可描述为:

式中, ξ —— 表面粗糙度的密度

β —— 曲率半径

κ —— 弹塑性变形程度

一般在1～2之间,具体计算方法如下:

如图2所示,当κ=1.5时,λ的曲线,当λ<3时,离合器进入混合摩擦状态,但微凸体所占比例不大,直到λ<1,微凸体面积开始迅速上升。

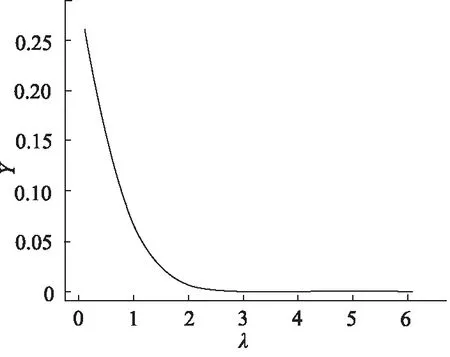
图2 面积比γ与膜厚比λ的关系

1.3 传递转矩模型

液黏调速离合器总剪切力主要由液压油产生的黏性剪切力τh和微凸体接触产生的粗糙摩擦剪切力τc两部分组成,因此其总剪切力可表示如下:

τ=τh+τc

(9)

计算黏性剪切力时引入Patir和Cheng平均流量模型中所提到的压力流量因子φf以及剪切流量因子φfs,可得其表达式如下:

其中,

摩擦剪切力可由单位接触压力与摩擦系数相乘得到:

τc=pcf

(12)

摩擦系数f由BERGEREJ[7]定义的曲线拟合函数:

通过对式(10)和式(12)与半径的乘积在摩擦副全域上进行积分,得到总传递转矩为:

被动盘角加速度可由牛顿第二定律得到:

式中, ω2—— 从动端角速度

J2—— 系统转动惯量

液黏调速离合器被动盘角速度更新表达式为:

2 液黏调速离合器仿真模型

基于MATLAB软件,对离合器模型中所有的方程进行建模与求解,其中求解式(1)很难得到其解析解,通常只能获得数值解。因此,采用有限体积法对式(1)进行求解,在结构网格下进行离散,离散方程中所出现的微分项用中心差分格式进一步离散,最后采用超松弛因子(SuccessiveOverrelaxaticMethod,SOR)方法对离散方程进行迭代求解,收敛条件满足下式:

(17)

为提高计算精度,收敛容许误差设定为1×10-5,通过网格无关性检验,可得到径向网格数量最佳为150,周向网格数量为80。同时考虑收敛性以及收敛速度,尝试不同的超松弛因子,最终确定雷诺方程的超松弛因数为1.95。液黏调速器接合模型计算流程如图3所示。

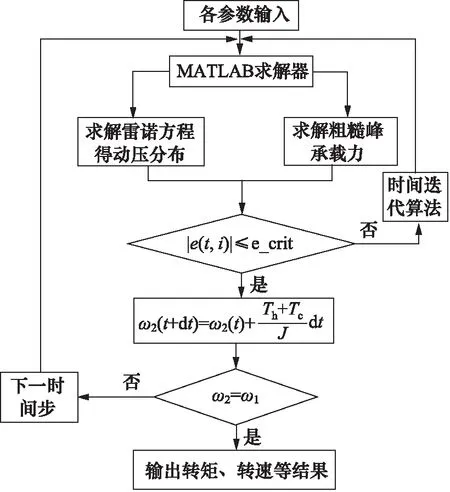
图3 离合器模型总体求解流程

图4为网格无关性验证图,取摩擦副半径方向中点处沿角度变化的压力作为网格无关性验证的监测点,网格数量分别为75×40,150×80,200×120,300×160。由此可知,网格数量75×40相差较大,150×80,200×120,300×160的压力趋势基本一致,因此150×80为最佳网格数量。

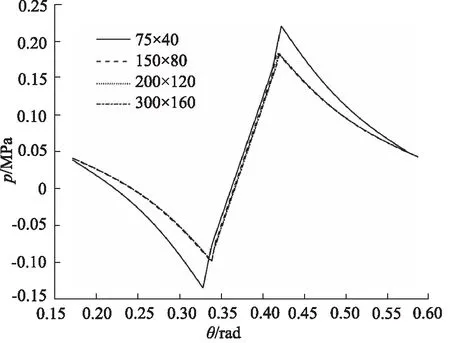
图4 网格无关性验证

3 仿真结果与分析

3.1 摩擦副结构参数

控制压力采用黄伟等[9]拟合得到的试验压力,将其作为仿真压力输入对离合器的接合过程进行仿真,其表达式如下:

ps=pmax(1-e-185t)

(18)

控制压力以及时间迭代算法所需要的时间步长设置为0.01s,将时间迭代算法中力误差准则e_crit设置为0.01,h_crit设置为0.01mm。表1为部分仿真结构参数。

表1 摩擦副结构参数

3.2 仿真分析

根据设定结构参数对液黏调速器接合过程进行仿真。如图5所示为离合器在接合过程中的油膜压缩速度v随时间t变化的曲线,在传动初期,油膜压缩速度快速达到峰值,然后再快速减小到一定值后达到稳定,这是由于液黏调速离合器接合初期为流体润滑阶段,接合压力处于迅速增大阶段,而且此时油膜承载力较小,使得油膜挤压速度上升较快。

如图6所示为油膜厚度h和被动盘转速ω2的变化曲线,在传动初期,活塞压力迅速增长,油膜厚度快速减小,在0.1 s左右离合器从流体润滑阶段进入混合摩擦阶段,此时微凸体开始接触,油膜厚度达到稳定。在接合初期,被动片角速度增速较为缓慢; 随着接合过程进行,油膜厚度减小,进入微凸体接触阶段,被动片角速度增速变快,直至被动盘角速度与主动盘角速度相等,接合过程结束。

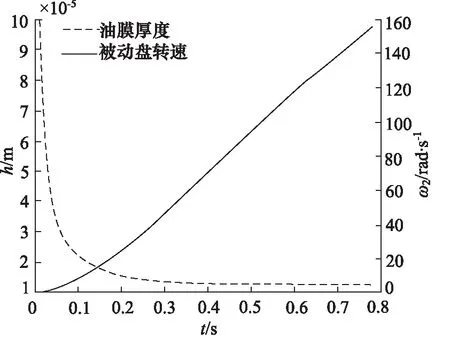
图6 油膜厚度和转速变化曲线

如图7所示为流体膜面积比与微凸体面积比随时间的变化曲线,在传动初期,摩擦副间全部由流体膜占据,在0.1 s左右,微凸体开始接触,但由于微凸体数量以及密度等参数的因素,其总体所占摩擦副的面积并不是很大,因此相对于流体膜面积,微凸体面积占比较少。

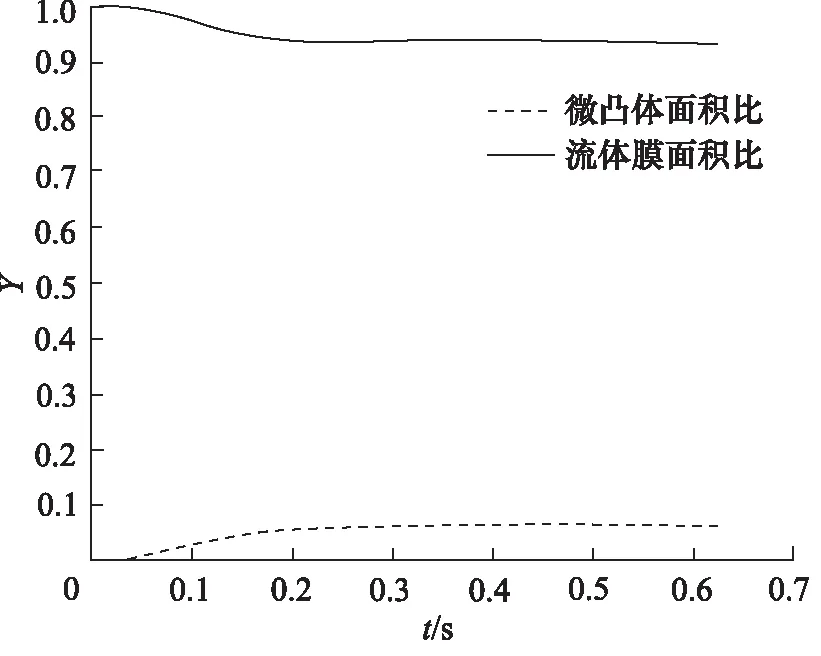
图7 流体膜与微凸体面积比例

如图8所示为承载力F变化曲线,可以看出,传动初期主要由油膜承载力与活塞压力平衡,在0.1 s进入混合摩擦阶段后,微凸体开始接触,活塞压力由油膜承载力与微凸体承载力共同承担,直到进入传动后期,活塞压力逐渐由微凸体承载力所平衡。

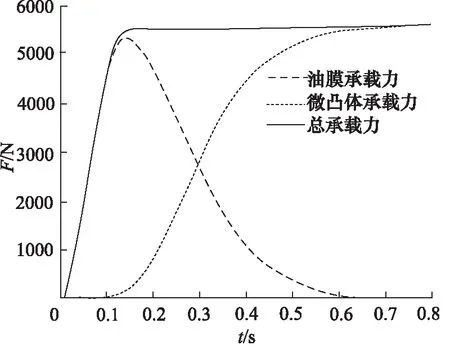
图8 承载力变化曲线

如图9所示为转矩T变化曲线。离合器接合过程处于流体润滑阶段时,黏性转矩随着接合过程的进行增大到峰值,这是由于在传动初期,油膜厚度迅速减小,被动盘角速度变化不大,因此黏性转矩迅速上升;当进入混合摩擦阶段后,微凸体开始接触产生摩擦转矩,此时,摩擦转矩和黏性转矩共同承担离合器的输出转矩,在此阶段,角加速度开始变大,相对转速减小,黏性转矩随之降低直至为零,而摩擦转矩慢慢占据主导地位。随着接合过程的进行,总传递扭矩先增大后减小,主要是由于黏性转矩和摩擦转矩共同作用的结果。

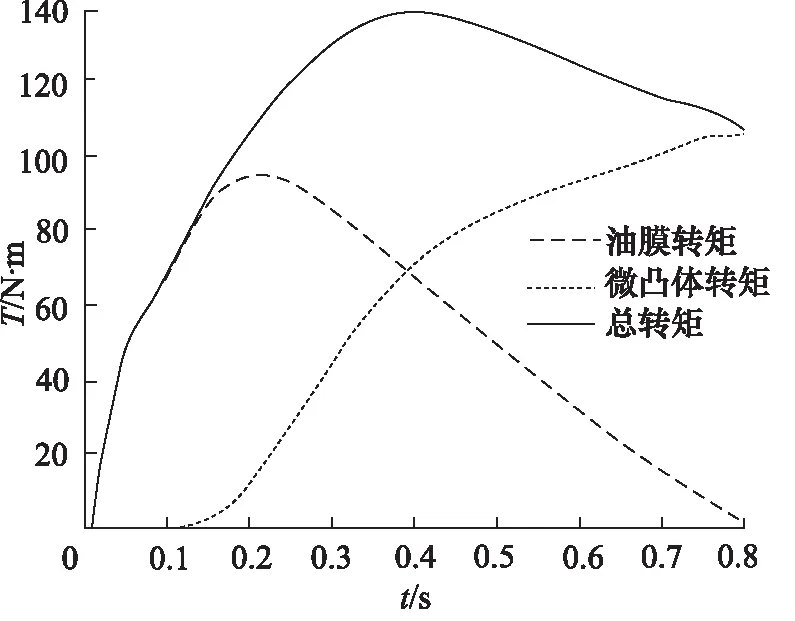
图9 转矩变化曲线

4 结论

通过有限体积法以及时间迭代算法建立了液黏调速离合器的数学模型,主要分析流体润滑以及混合摩擦两个阶段的接合特性,可以得到:

(1) 液黏调速离合器流体润滑阶段时间较短,油膜厚度变化很快,黏性扭矩处于快速上升阶段;

(2) 在0.1 s左右,液黏调速离合器接合进入混合摩擦阶段,在此阶段摩擦扭矩迅速上升,黏性扭矩开始减小,摩擦扭矩占据主导地位;

(3) 液黏调速离合器被动盘角加速度在混合摩擦阶段大于流体润滑阶段,因此角速度在混合摩擦阶段变化更快。