自抗扰控制的单双泵控分布式挖掘机液压系统

张树忠, 刘 意, 李 苏, 张雪峰

(1.福建工程学院福建省智能加工技术及装备重点实验室, 福建福州 350108; 2.福州大学机械工程及自动化学院, 福建福州 350108)

引言

液压挖掘机是目前使用最广泛的工程机械之一。传统的挖掘机是阀控系统驱动,通过阀来控制差动缸的运动速度和方向,存在体积大、结构复杂、油液使用量多、能量损失大等问题[1]。随着变频技术的发展,泵控直驱技术成为一大研究热点[2]。对于差动缸两腔面积不同而引起的流量不匹配问题,IVANTYSYNOVA M[3]最先提出了采用液控单向阀补偿来平衡不对称流量,并将其用于液压挖掘机,与负载敏感阀控系统相比,可节能50%以上。针对负载力发生突变时,液控单向阀并不能很好的控制两侧的流量差[4],导致速度波动,例如挖掘机斗杆,为了更好的平衡流量差,学者对泵控结构进行改进。权龙等[5]针对泵控差动缸位置控制设计6种不同组合液压回路方案。景健等[6]设计了三配流窗口轴向柱塞泵,通过设置配流盘窗口面积,使两个油口的油液分别与差动缸两腔的流量相匹配,第三个油口完全平衡系统的流量差。

泵控系统在工程应用中存在系统动力学阶数高、非线性强等控制难点,使其难以完成高精度的执行器运动轨迹跟踪。为了提高系统的控制性能,大量学者提出多种控制算法。LIN Y等[7]针对电静液作动器(Electro-Hydraulic Actuator,EHA)提出一种泵控系统的离散滑模控制策略,保证了系统在变摩擦力影响下的较高控制精度;AHN K K等[8]提出了一种自适应反步位置控制方法,通过在线参数自适应的方式处理伺服电机-泵控制系统的参数不确定性;HELIAN B等[9]将泵控系统研究中通常忽略的伺服电机-泵高阶动力学考虑到系统运动控制器设计中,处理非线性和不确定性等问题,改善了系统运动控制精度;自抗扰控制算法是韩京清教授在20世纪80年代在“基于误差来消除误差”的控制策略上研究发展而成的一种非线性 PID 控制思想[10]。自抗扰控制(Active Disturbance Rejection Control, ADRC)算法结构简单,只需要控制系统的输入、输出信息,基本不需要被控对象的数学模型,具有很强的鲁棒性。GAO Z[11]将非线性ADRC简化为线性ADRC结构,并把ADRC的所有参数都变为带宽的函数,简化调参个数,推动ADRC重新成为研究热点。

为提高挖掘机系统效率和克服负载突变时的速度波动问题,提出一种单双泵控混合分布式液压系统。此外,针对泵控系统的高阶数和非线性问题,设计自抗扰控制器,以提高系统响应速度及抗扰能力。

1 负载敏感阀控系统与分布式泵控系统结构

1.1 负载敏感阀控液压系统

某微型挖掘机的负载敏感阀控液压系统(见图1),主要由伺服电动机、单向定量泵、溢流阀、梭阀、比例流量阀和差动缸等组成。该系统采用伺服电机驱动定量泵为三个执行器供油,通过调节电机转速进而改变泵的输出流量,使比例阀进出口压差维持在2 MPa,实现与负载无关的独立流量控制。

1.伺服电机 2.单向定量泵 3.溢流阀 4.比例流量阀5.差动缸 6.梭阀

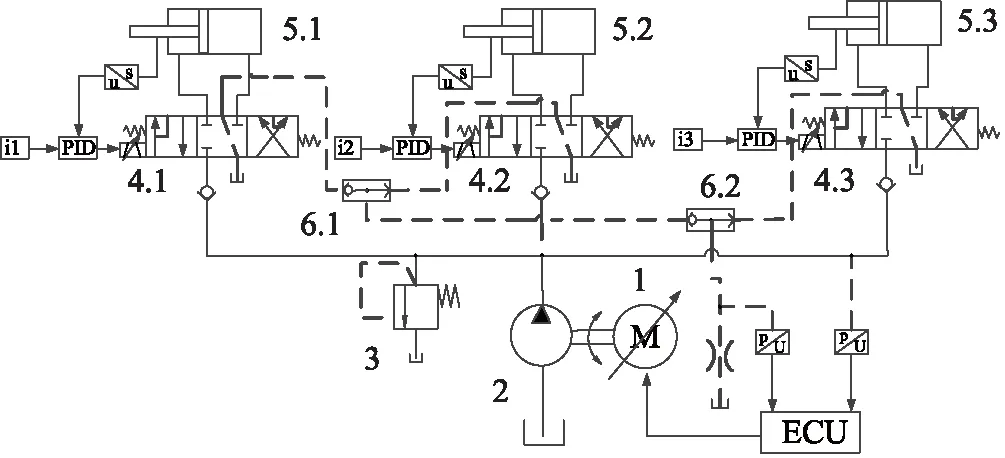
1.2 单双泵控混合分布式挖掘机液压系统

如图2所示,单泵控单元通过液控单向阀来平衡流量,所需元件较少、结构紧凑,但存在负载力突变的四象限工况下会出现较剧烈的速度波动[12]。由于斗杆和铲斗在工作时会在四象限之间切换工作,若采用单泵控单元必然导致速度波动;而通过并联一个小排量泵来平衡流量,能较好地解决此问题。基于上述分析,本研究提出一种单双泵控混合分布式挖掘机液压系统,如图2所示。该系统中二象限工况的动臂采用单泵控单元,四象限工况的斗杆和铲斗则采用双泵并联式泵控单元。

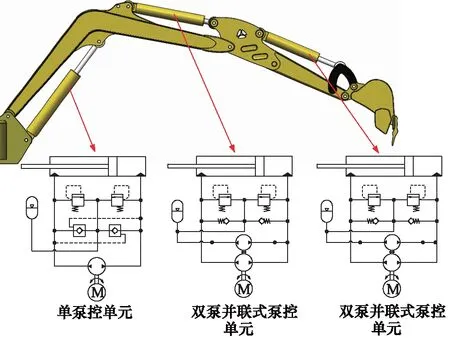
图2 单双泵控混合分布式系统

2 建模与参数匹配

2.1 附加泵控单元的动力学模型

对某一吨级微型挖掘机进行拆卸,通过测量、称重得到各零部件的尺寸和质量,运用三维扫描仪对其进行扫描,结合Geomagic Design X逆向工程和Pro/Engineer正向设计得到各零部件三维模型,并装配得到整机模型。最后,将三维模型导入MATLAB Simscape中,建立挖掘机机械结构多体动力学模型,其结构参数如表1所示。

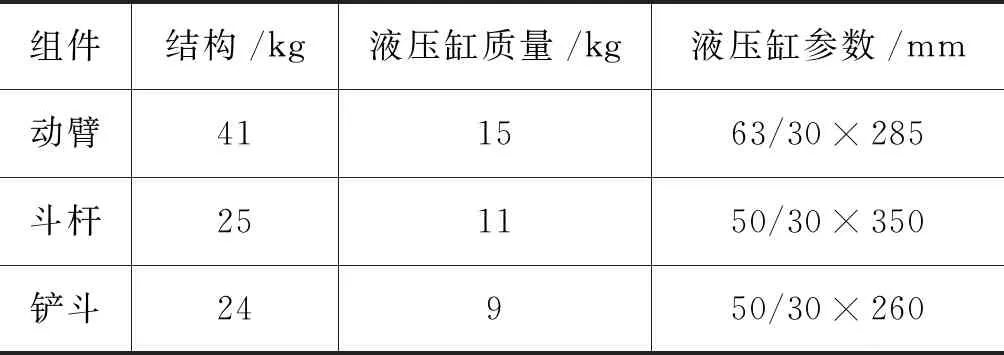
表1 工作装置结构参数

该负载敏感阀控挖掘机液压系统质量主要集中在挖掘机后机座,故在动力学建模中可忽略液压系统质量对工作装置的影响。

而在单双泵控混合分布式挖掘机动力学模型中,根据工作装置结构,在其上附加了三个泵控单元,如图3所示。每个泵控单元主要由蓄能器、电机、泵/马达及阀组等辅助元件组成。

图3 附加泵控单元的动力学模型

每个泵控单元约20 kg,其元件参数和质量如表2所示。

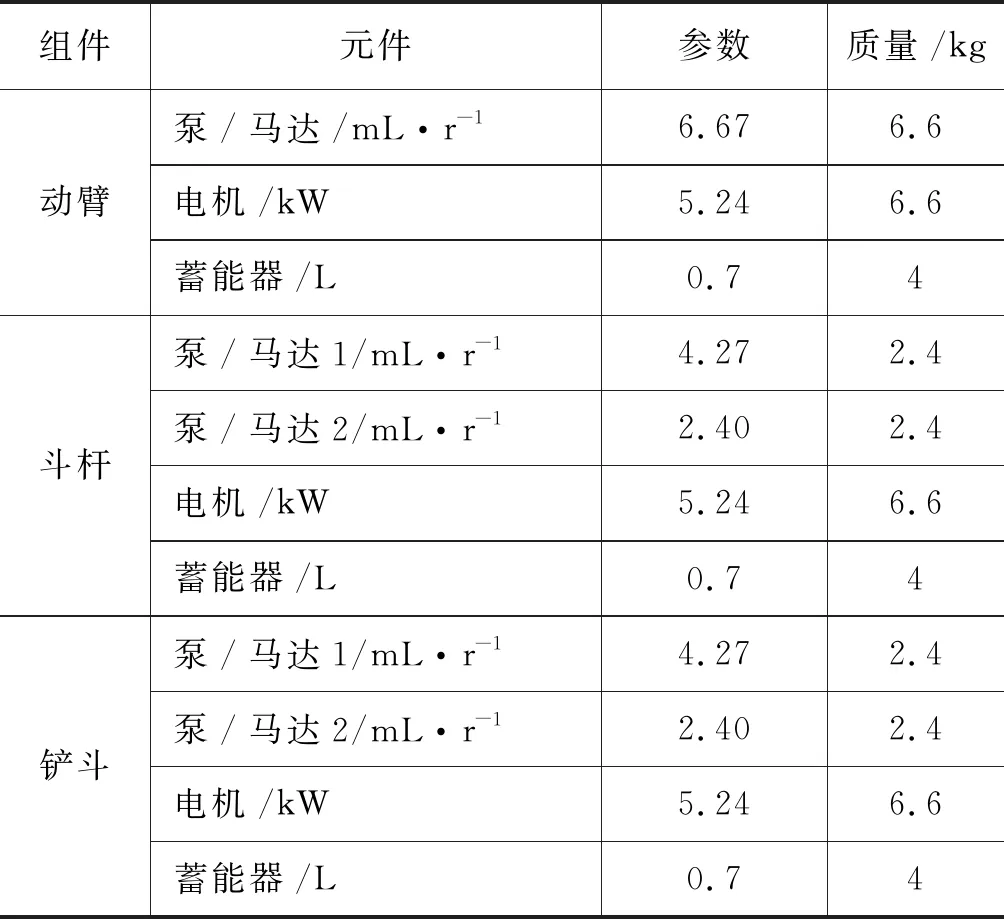
表2 泵控单元元件参数和质量

2.2 液压系统模型

负载敏感阀控系统主要由比例换向阀、油液弹性模量、泵、管路及液压缸等模型组成;单双泵控单元还包括蓄能器、单向阀以及液控单向阀模型等。

1) 比例阀模型

比例阀可简化为由2个两两互通的节流口组成[13](即PA与BT、PB与AT),如图4所示。

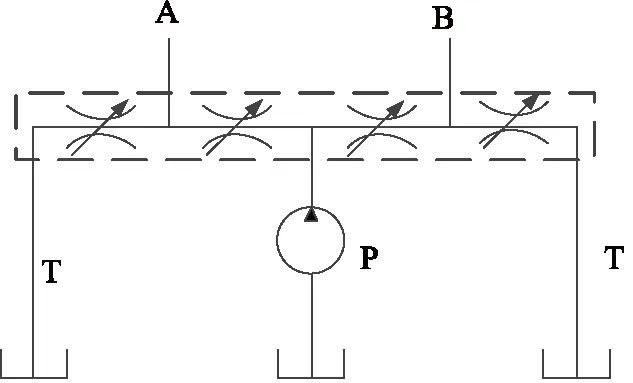
图4 比例阀原理图

通过节流阀流量公式计算:

式中, Cq—— 流量系数

A0—— 节流口流通面积

Δp —— 压降

ρ —— 液压油密度

利用一维(1-D)查表建立比例阀输入电压-通流能力的函数关系。根据Danfoss公司PVG32型比例阀样本[14]中的特性曲线,用式(2)计算出一维表的参数KV:

此外,比例阀的动态特性可以近似为一阶惯性系统,如下式:

式中, τ —— 时间常数

2) 油液体积弹性模量

在仿真中采用油液体积弹性模量[15]模型如下:

式中, p0—— 初始工作压力

p —— 当前工作压力

N —— 气体多变指数

X0—— 油液中相对的空气含量

βliq—— 特定温度下的体积油液弹性模量

3) 蓄能器

式中, VoAcc—— 液压蓄能器在初始状态下的工作容积

poAcc—— 液压蓄能器在初始条件下的压力

VAcc—— 蓄能器在工作状态下的容积

pAcc—— 蓄能器在工作状态下的压力

4) 液控单向阀

普通单向阀与液控单向阀建模相似,根据MATLAB/Simscape中液压元件库中的相关模型对其进行建模[16]。

式中, Cd—— 流量系数

A —— 节流面积

p —— 两侧压差

pcr—— 湍流最低压力

pe=pA+pXkp-pB

(7)

式中, pA,pB——A侧、B侧压力

pX—— 先导压力

kp—— 先导比

pe—— 等效压力

pcrack—— 开启压力

pmax—— 最大压力

Aleak—— 泄漏面积

Amax—— 最大开启面积

5) 泵/马达

式中, qPM—— 泵/马达实际流量

n —— 泵/马达转速

V —— 泵/马达排量

qL—— 泵/马达泄漏流量

根据实测数据,利用最小二乘法求出泵泄漏模型各部分增益系数[17]:

式中, α,β,γ —— 回归系数

6) 液压缸

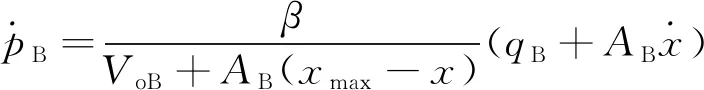
式中, pA,pB—— 液压缸两腔压力

AA,AB—— 液压缸两腔有效面积

qA,qB—— 液压缸两腔进出口流量

x —— 活塞位移

xmax—— 活塞最大行程

β —— 油液有效体积弹性模量

V0A、V0B—— 液压缸两腔初始容积

液压缸两腔面积比和等效压力定义如下:

a=AA/AB

(13)

pL=pA-apB

(14)

式中, a —— 面积比

pL—— 等效压力

则液压缸的力平衡方程可表示为:

式中, Fr—— 黏性摩擦力

FL—— 外部负载力

其中, 摩擦力Fr采用经典的摩擦力模型(LuGre模型), 模型中参数参考文献[13],实现摩擦力随着速度而非线性变化。

根据上述数学模型,在MATLAB/Simulink中搭建液压系统模型,包括负载敏感阀控系统、单泵控单元和双泵并联式泵控单元,如图5～图7所示。

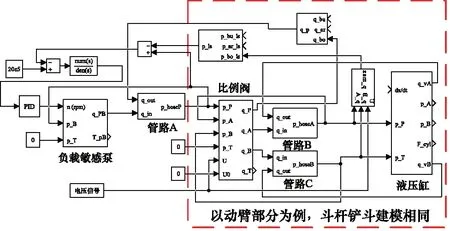
图5 负载敏感阀控系统仿真模型

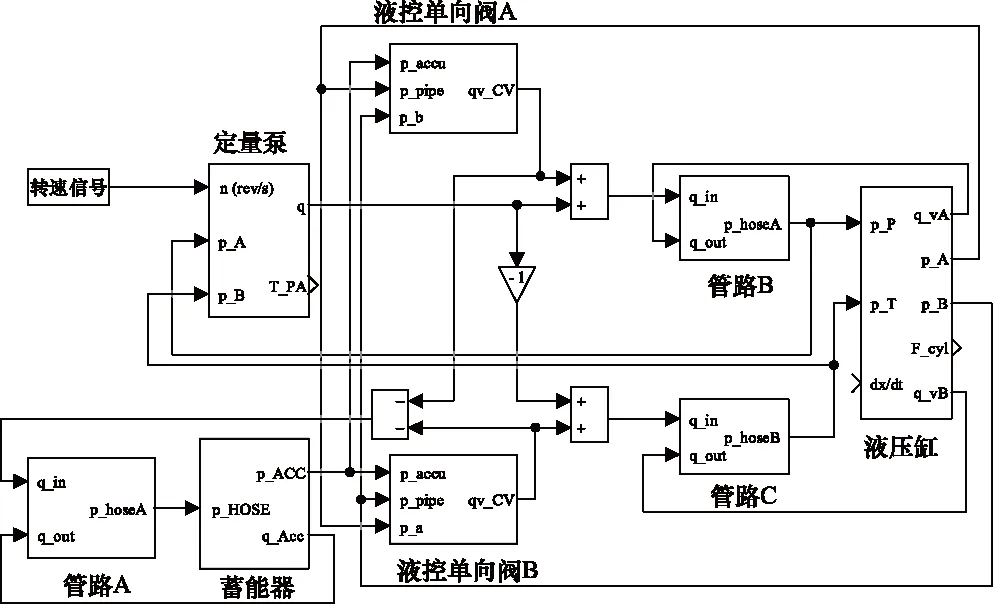
图6 单泵控单元仿真模型

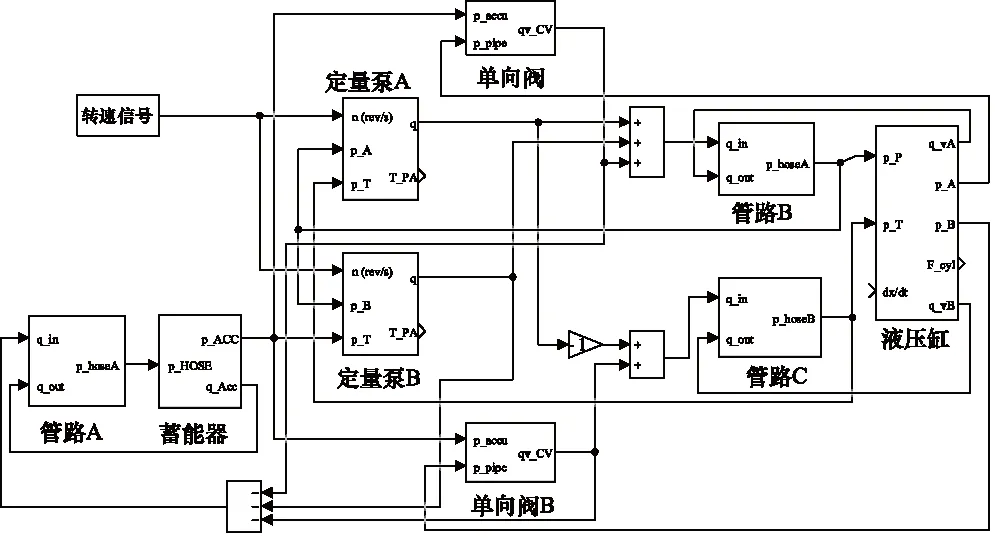
图7 双泵并联式泵控单元仿真模型

3 控制器设计

3.1 PID

1) 负载敏感阀控系统

负载敏感阀控系统中,负载敏感泵为系统供油,通过PID控制比例流量阀的开口度,实现对液压缸的位置控制,其PID参数如表3所示。

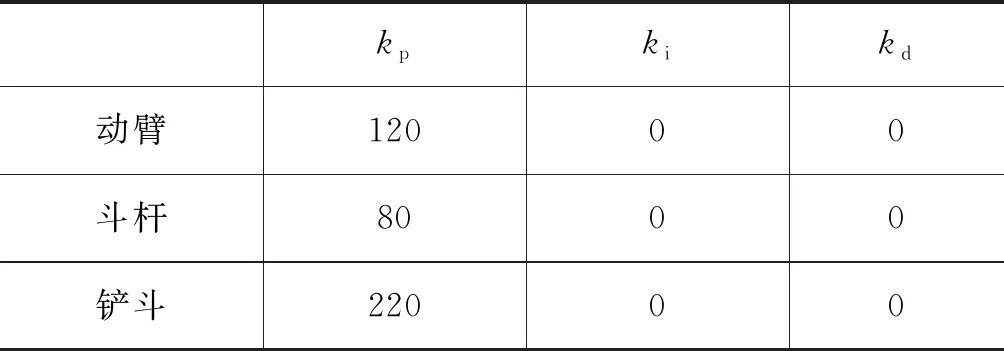
表3 负载敏感阀控系统PID参数

2) 单双泵控混合分布式系统

单双泵控混合分布式系统三组PID控制器独立控制三个泵控单元,通过改变泵的转速,实现对液压缸的位置控制,其参数如表4所示。

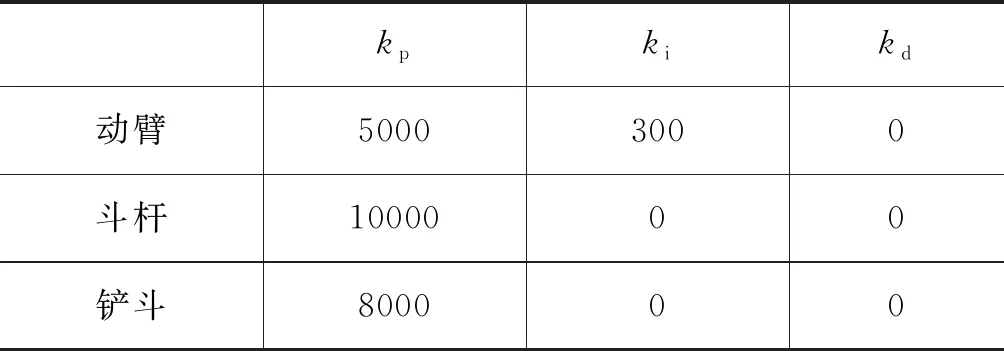
表4 所提出泵控分布式系统的PID参数

3.2 ADRC

针对泵控系统动态响应慢及抗扰能力差的问题,设计自抗扰控制器。自抗扰控制器由PD控制器、扩张观测器组成,通过观测器对各状态变量和扰动进行观测,运用PD控制器提高控制精度并减少系统震荡,其控制结构框图如图8所示。

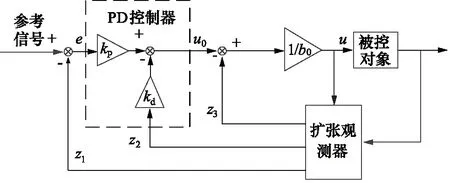
图8 ADRC控制结构图

假设初始位置处于液压缸行程中心位置来回运动,能得到以下近似值:

式中, Vt—— 液压缸总容积

由表2可知,无论是单泵控液压系统还是双泵并联式泵控液压系统,大腔排量始终为Q1=QPM=ωDs,小腔流量为Q2=aQ1=aωDS。

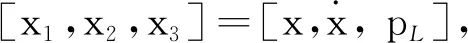
式中, k —— 增益系数,k=1+a2

ci—— 液压缸泄漏系数

所建状态方程中,控制量ω与外扰并不在同一通道中,无法通过控制输入直接对外扰进行补偿,为便于控制设计,对模型进行降阶处理。

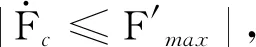
Dsω-A1x2-cipL=0

(18)

将式(18)代入式(17)中得到降阶后的状态方程:

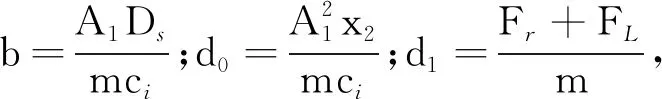
f=-d0-d1+(b-b0)u

(20)

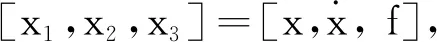
扩张观测器为可根据系统的输入输出来估算系统状态及扩张状态的观测器,表达为:

式中, z —— 各状态变量的观测值

β —— 状态观测器的观测增益

fal(e,ai,δ) —— 非线性投影函数

反馈控制律部分基于PD控制原理根据状态变量观测值产生反馈控制量:

u0=kp(r-z1)-kdz2

(23)

式中, kp,kd—— 状态反馈控制的控制参数

r —— 参考信号

结合扩张状态的观测量,则被控对象的控制输入可表示为:

由式(22)和式(23)可知,ADRC需要整定的参数主要有β01,β02,β03,kp和kd。基于文献[11]中频率尺度的概念,将PD控制器和扩张状态观测器以线性形式表示,以控制器带宽ωc和观测器带宽ω0为各自的唯一变量:

根据文献[18]中的线性ADRC参数整定方法对ωc和ω0进行整定。

分别为单双泵控混合分布式挖掘机液压系统的三个泵控单元设计自抗扰控制器,相应的参数设置如表5所示。

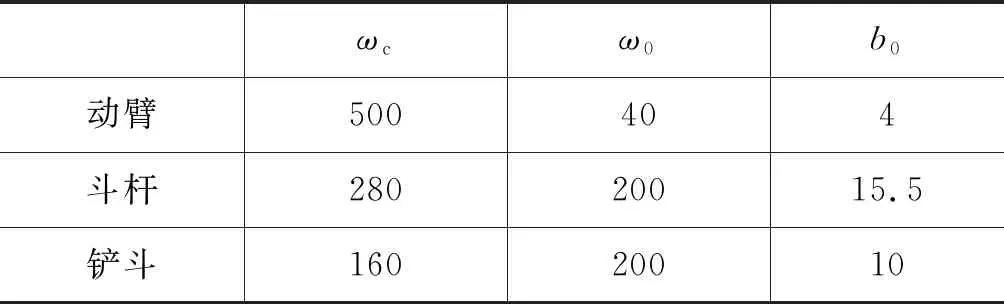
表5 所设计ADRC参数

4 仿真分析

为模拟挖掘机工作过程,采用JCMAS (日本建筑机械化协会标准) 的典型挖掘循环作为模型的输入。以下降→挖掘→提升→放铲→回位动作作为一个典型循环工况,其动臂、斗杆、铲斗液压缸的位置s和速度v信号如图9所示,时间为22 s。

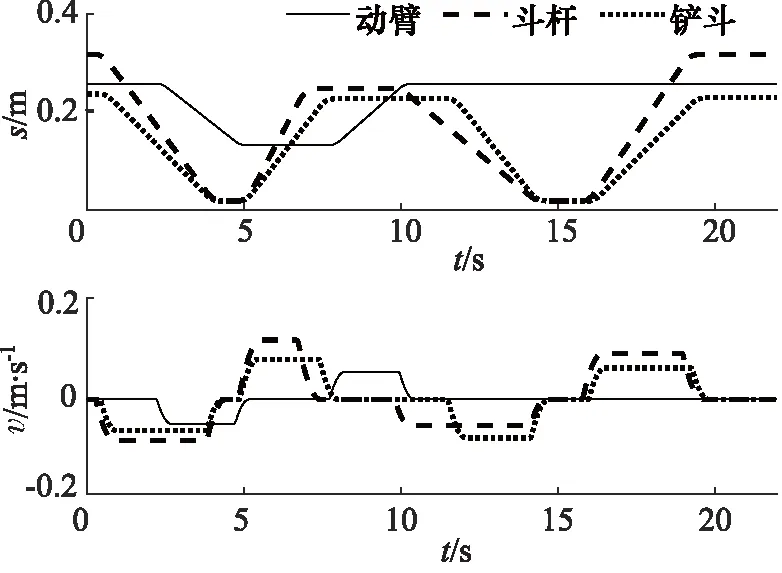
图9 位置-速度参考信号

4.1 四象限工况下的速度-负载特性分析

以PID控制的双泵并联式泵控单元的斗杆为例(见图10),在典型挖掘循环下,虽然存在四象限工况切换(①～④时刻历经4次负载力方向改变), 但速度几乎无波动,可见双泵并联式泵控系统能较好地抑制负载突变导致的速度波动。

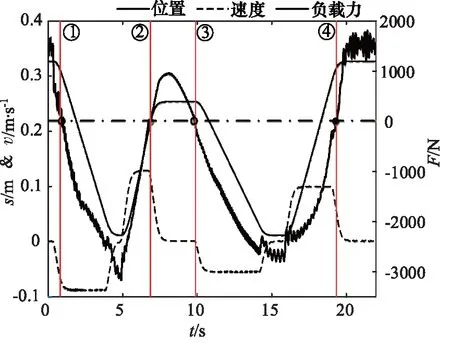
图10 速度-负载特性

4.2 跟踪特性与能耗

1) PID阀控与PID分布式泵控的比较

在跟踪特性方面:如图11所示,与PID阀控系统相比, 由于泵控系统的高阶非线性, 整体响应速度较慢,采用PID控制的泵控系统位置跟踪存在较明显滞后,三个缸的均方根误差和最大误差平均值分别增加了2.5,7.5 mm(见图12),跟踪精度有所降低。尤其是采用单泵控的动臂,加上负载力大的影响,在①(3～6 s)和②(7～13 s)阶段滞后较大。

图11 PID阀控、PID泵控以及ADRC泵控的工作装置位置跟踪曲线

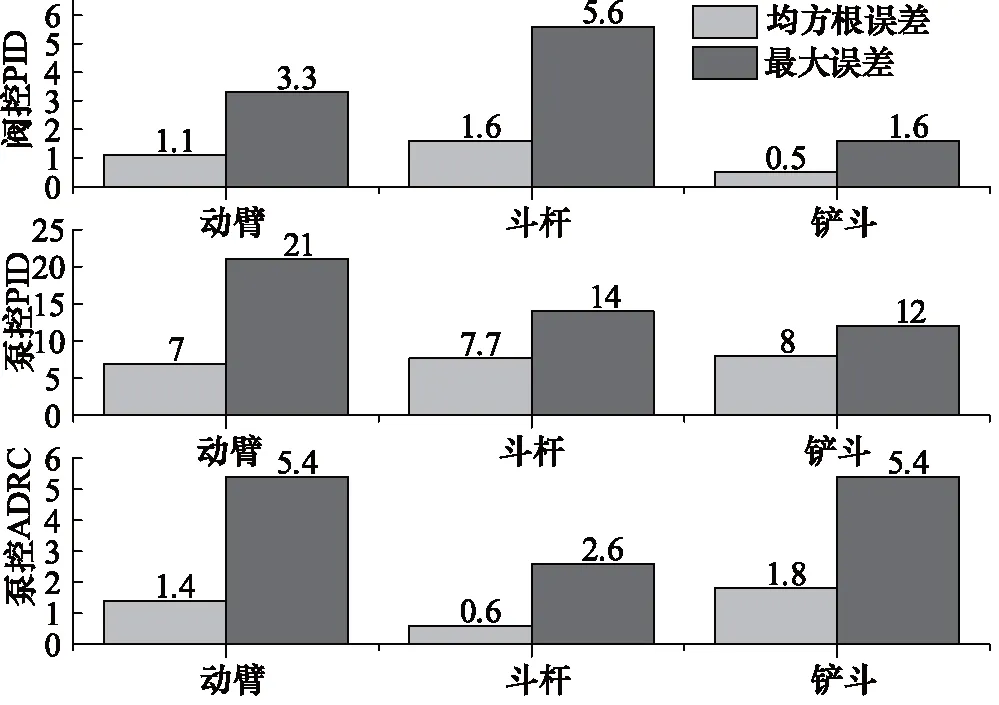
图12 跟踪误差对比

在能耗方面:由系统的能耗分布图(见图13),可知PID阀控存在大量的节流损失,能耗较大为10.5 kJ,系统效率仅为21%;而PID泵控系统减少了节流损失,能耗降低了62%,系统效率提高到60%。

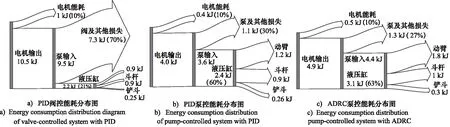
图13 能耗分布图

2) PID和ADRC分布式泵控的比较

在跟踪特性方面:与PID控制器相比,虽然所设计ADRC存在超调和震荡(见图11中A区),稳定性略差,但能有效提高系统的响应速度,三个缸的均方根误差和最大误差平均值与PID阀控的基本相当(见图12),具有良好的位置跟踪性能。

在能耗方面:由图13b和13c对比可知,与PID控制器相比,ADRC控制系统受超调和震荡影响,系统能耗有所增加,特别是动臂的能耗由1.2 kJ增加到1.8 kJ;系统总能耗由PID控制的4.0 kJ提高到4.9 kJ(能耗增加了22.5%),但依然比阀控系统能耗低53%,系统效率达到63%。

5 结论

基于挖掘机工作装置各液压缸的速度-负载特性,设计了一种单双泵混合分布式泵控系统及其自抗扰控制器,结果表明:

(1) 所设计双泵并联泵控单元,能较好地抑制斗杆、铲斗在四象限工况下负载力突变时的速度波动;

(2) 负载敏感阀控系统响应速度快,位置跟踪性能好,但系统能耗大且效率低,仅为21%左右。而采用所提出的泵控分布式系统后,系统至少降低了能耗53%,系统效率提高了60%;

(3) 在所提出泵控分布式系统中,与PID相比,所设计ADRC在信号变化时存在超调和局部震荡,系统能耗有所增加,但跟踪精度高,可获得与阀控相当的跟踪性能。